Abstract
Industrial robots have become a crucial tool for milling large and complex surfaces. The dynamic characteristics of a robotic structure significantly influence milling accuracy and efficiency. Accurate identification of these dynamic parameters during operation is essential for vibration suppression and enhancing machining performance. Notably, the dynamic characteristics of a robot in operation differ from those in a static state. Operational modal analysis (OMA) enables the identification of structural dynamic parameters under operating conditions, but it necessitates input signals that approximate white noise, which is not met by the excitation forces during typical robot operations. Moreover, OMA is primarily applied to fixed structures, such as buildings and bridges, whereas the dynamic characteristics of robots vary as their poses change during operation. To address these challenges, this paper proposes an autonomous modal analysis method that considers the dynamic spatial sensitivity of robots and the randomness of the excitation frequency band and direction. Firstly, to mitigate the impact of pose changes on modal parameter identification, a method for predicting the sensitivity of natural frequencies based on structural modal shapes is proposed. This approach limits the range of the robot’s self-excitation motion based on dynamic spatial sensitivity analysis. Secondly, the necessary condition for the randomness of the excitation force direction is established, requiring that the torque projection matrix be of full rank. Building on this, a broadband random signal meeting the requirements of white noise is generated through multi-joint random acceleration and deceleration movements. Finally, the efficacy of the proposed autonomous modal analysis method is validated through multi-joint combined self-excitation modal analysis experiments.
Similar content being viewed by others
Introduction
Robot machining has emerged as a significant method for complex surface milling, owing to its low cost, exceptional flexibility, extensive working range, seamless integration of intelligent sensing technology, and ease of achieving collaborative operations1. Accurate analysis of the robot’s structural dynamics is crucial for vibration analysis and suppression during the milling process2.
In practical machining scenarios, the robot’s dynamic characteristics are influenced by numerous of factors3,4. Changes in the robot’s pose alter its structural dynamic properties. Mousavi et al.5,6 developed a finite element model of the robot incorporating flexible links and joints. They employed a matrix structural analysis method to compute variations in the robot’s natural frequencies at different points along the machining path. The findings revealed that the variation in natural frequencies could reach up to 40% along a linear machining path. Huynh et al.7,8 constructed a multi-body model of the robot, incorporating three degrees of freedom at flexible joints. Using this model, they analyzed changes in natural frequencies, damping ratios, and modal shapes at various locations within the workspace. The results indicated that both natural frequencies and modal shapes varied with different postures. Do et al.9 formulated an analytical dynamic model for robotic manipulators with rigid links and flexible joints. They examined the impacts of gravity forces, external forces, and control parameters on the dynamic characteristics, linearizing the model to facilitate the calculation of modal parameters for the robot structure at any posture.
Mejri et al.10 identified the frequency response function (FRF) of the tool tip at selected positions within the robot’s workspace using experimental modal analysis. Karim et al.11 performed experimental modal analysis to ascertain the natural frequencies at 23 distinct points in the robot’s workspace. The results demonstrated that the variation in low-order mode natural frequencies could reach 50%, with the variation differing across regions of the workspace, indicating that simple linear interpolation predictions were inadequate. Chen et al.12,13 predicted the FRF at different postures using a combination of substructure coupling analysis and experimental modal analysis. However, due to the numerous joints and connectors in the robot’s structure, the computational process was complex, and the accuracy of the results heavily relied on the node parameters. Nguyen et al.14 used impact testing modal analysis and a data-driven model based on Gaussian process regression to predict modal parameters at different postures of industrial robots, thereby optimizing the robot machining process. Tunc et al.15 investigated the variations in the end-effector FRF of a Fanuc F200iB six-degree-of-freedom robot as a function of direction and posture, using impact testing modal analysis. The study revealed that the sensitivity of natural frequencies and frequency response amplitude to position changes varied across directions. Similarly, Wang et al.16 collected data through experimental modal analysis and employed a random forest machine learning algorithm to establish a position-dependent dynamic characteristic prediction model, with joint angles as inputs and modal parameters at corresponding postures as outputs. Lei et al.17 used a Multi-Task Gaussian Process (MTGP) regression model to predict the tool tip FRFs of machine tools for different positions and tools.
Changes in joint velocity and the contact state of the joint bearing also affect the robot’s structural dynamics18,19. L.T. Tunc et al.20 observed a difference in the end-effector FRF between the robot’s quasi-static operation and its stationary state. The predicted machining stability based on the FRF during quasi-static operation aligned more closely with actual cutting experimental results. Y. Mohammadi et al.21,22,23 used cubic polynomial fitting for the arm joint stiffness and damping terms. The results showed that high-order FRFs based on nonlinear stiffness and damping coefficients provided a better fit to the frequency response curves obtained from experiments.
To accurately identify the modal parameters, to accurately identify the modal parameters of the robot’s structure during operation, researchers have adopted the operational modal analysis (OMA) to study the dynamic characteristics of the robot. Mokdad et al.24 employed the autoregressive parameter identification model of OMA to ascertain the structural modal parameters of the robot during grinding operations. The results indicated that, under two distinct operating speeds and boundary conditions, the natural frequencies of the robot shifted from low-order to high-order, with a variation rate of approximately 10%. Maamar et al.25,26 used the transfer ratio function, based on operational modal analysis, to identify the structural modal parameters of a milling robot during operation. Their study revealed that, compared to the stationary state, there was a discrepancy in the robot’s end-effector frequency response function (FRF). The machining stability predicted using the FRF during operation aligned more closely with the actual cutting experimental results. Nguyen et al.27,28 identified the tool tip FRF of the KUKA KR500-3 robot in its working state by concurrently measuring the milling force and vibration response during the milling operation. They compared these results with the tool tip FRF obtained through impact testing modal analysis and observed a shift in the peak of the natural frequency. In 2023, Deng et al.29 noted that a robot’s FRF is influenced by various factors, such as pose, operating state, and external excitation. They removed the harmonic components of the vibration signals using a matrix notch filter and conducted operational modal analysis (OMA) using least-squares complex frequency domain decomposition. In the same year, Ge et al.30 conducted operational modal analysis based on normal milling signals from the robot and proposed using the variational mode decomposition-OMA (VMD-OMA) method to eliminate amplitude-modulated and frequency-modulated (AM-FM) harmonic components during the milling process. This approach facilitated the extraction of random response signals and employed the stochastic subspace identification (SSI) algorithm to identify the dynamic parameters.
In summary, the robot’s OMA is primarily performed during the milling process. During normal milling, the input signal is a non-white noise signal, and the resulting response signal requires further processing. Common methods for processing include measuring the cutting force, using filtering algorithms31,32, or employing transfer function analysis to extract the random response components of the signal, thereby enabling modal parameter identification.
To address the above issues, this paper proposes a robot free-running self-excitation autonomous modal analysis method that combines dynamic sensitivity coefficients and torque projection matrices. The main differences between this method and existing approaches are as follows: First, the random acceleration and deceleration movements of the joints is used to ensure that the input signal is white noise, thus eliminating the complex procedure for further processing of the response signal. This enables the automatic identification of modal parameters during the robot’s operation. Existing methods that use random acceleration and deceleration to generate excitation primarily focus on the randomness of excitation energy, without considering the randomness of the excitation force direction. This paper, however, extends this approach by incorporating the torque projection matrix to introduce the condition of directional randomness. Second, this paper accounts for the impact of posture changes on random acceleration and deceleration movements. Through dynamic spatial sensitivity analysis, the joint motion range is controlled to minimize the influence of posture variations on the robot’s dynamic characteristics during operation, thereby enabling autonomous modal analysis across the robot’s entire workspace.
The structure of this paper is organized as follows: In Sect. 2, the concepts of dynamic spatial sensitivity and the torque projection matrix are introduced. The relationship between the sensitivity coefficient and the structural modal shapes is along with. Section 3 analyzes the dynamic spatial sensitivity of the ABB 6660 robot and verifies the relationship between the sensitivity coefficient and the modal shapes. In Sect. 4, an indicator for the randomness of the excitation signal direction based on the torque projection matrix, is established. The randomness of excitation energy and direction for multi-axis combined self-excitation is also analyzed. In Sect. 5, multi-joint combined free-running self-excitation modal analysis experiments are conducted on the ABB 6660 robot. The structural modal parameters in the operating state are identified and compared with the identification results obtained under various conditions.
Dynamic sensitivity coefficient and torque projection matrix
To effectively identify structural modal parameters during multi-joint combined self-excitation motion of a robot, this paper proposes dynamic spatial sensitivity analysis and the torque projection matrix. By utilizing dynamic spatial sensitivity analysis, we can determine the operating range of joint angles during self-excited motion. Additionally, based on the torque projection matrix, we can ascertain the motion direction of each joint in the multi-joint combined movement, ensuring that the energy and direction of the excitation signal meet the white noise requirements.
Dynamic sensitivity coefficient
In order to evaluate the influence of the angular displacement of the joint on the dynamic characteristics of the robot, the dynamic sensitivity coefficient εi of the i order mode is defined as the ratio of the change of natural frequency to the original natural frequency.
where ωi.a. represents the natural frequency of the ith order mode before the change of robot motion state; ωib represents the natural frequency of the ith order mode after the change of motion state; n represents the maximum modal order of the system in the frequency band under consideration. The dynamic equation of robot structure is as follows
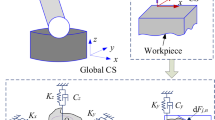
where M represents the mass matrix of the structure; C represents the structural damping matrix; K represents the stiffness matrix; x represents the displacement vector of structural vibration; \(F\left( t \right)\) represents the external stimuli to the structure. The characteristic equation of the structure
where ωi represents natural frequency of the ith mode of the structure; \({\left\{ \phi \right\}_i}\) represents the ith mode of the structure; When the mass mr is added to any r degree of freedom of the structure, the dynamic equation of the structure
where \(\Delta m\)represents the additional mass is introduced into the mass matrix
The characteristic equation of the structure after adding mass
where ωi represents natural frequency of the first mode after adding mass to the structure; \({\left\{ \phi \right\}_i}^{\prime }\) represents the ith mode of the structure after adding mass; When the additional mass is small enough, the mode of the structure before and after the additional mass is basically unchanged
The eigenequation (3) before and after the additional mass is subtracted from Eq. (6), and the Eq. (7) is substituted
When \({\left\{ \phi \right\}_i}\) is the mass normalized mode vector of the structure, the above formula can be further expressed as
Divide both sides of the above equation by ωi2 and take the root of it
where \({\phi _{ir}}\) represents the mode component of the ith mode vector of the structure at the position of r degree of freedom. By bringing the above formula into Eq. (1), the modal expression of the dynamic sensitivity coefficient of the ith mode can be obtained
where \({\varphi _{ir}}\) represents the ith normalized modal component of the structure at the position of r degree of freedom.
According to Eq. (10), the dynamic sensitivity coefficient is proportional to the modal shapes of the structure. The larger the structure’s modal shapes, the greater the change of natural frequency due to variation in joint angles; The smaller the modal shapes of the structure, the less the change of natural frequency caused by joint angle degree variation. The validity of this analysis method will be verified experimentally in Sect. 3.
Torque projection matrix
The forces and torques applied on the end-effector of robot can be represented as \(\:F={\left(Fx,Fy,Fz,mx,my,mz\right)}^{T}\). The forces and torques of each joint of robot can be combined as the joint vector \(\:\tau\:={\left({\tau\:}_{1},{\tau\:}_{2},{\tau\:}_{3},{\tau\:}_{4},{\tau\:}_{5},{\tau\:}_{6}\right)}^{T}\). When the driving torques produced from the rotation of the joints cause an output at the end-effector, the sum of the virtual work at each joint is given by:
Where \(\:\delta\:q\) represents the virtual displacement in the joint space. The virtual work of the end-effector is given by:
where \(\:D\) represents the virtual displacement in the workspace. Since there is a geometric relationship between the forces acting on the end-effector and the joint displacements, it is assumed that the virtual displacement in the workspace is \(\:\varvec{D}=\varvec{J}\varvec{\delta\:}\varvec{q}\), where \(\:\varvec{J}\) represents the Jacobian matrix. According to the principle of virtual work, the virtual work produced by the change in the joint vector is equal to the virtual work in the workspace. Therefore, we have:
Simplify:
Equation (15) represents the mapping relationship between the generalized external forces at the robot’s end-effector and the joint torques can be expressed as. The velocity Jacobian matrix can be written as:
Where \(\:\dot{\varvec{q}}\) represents the joint velocity vector and \(\:\dot{\varvec{x}}\) represents the operational velocity vector. When the robot undergoes self-excited motion based on joint motors, the forces acting on the robot system are generated by the driving torques of each joint. At this point, the input forces \(\:\left\{{f}_{1},{\:f}_{2},\:\cdots\:,\:{f}_{d}\right\}\) combined form the input torques vector \(\:\varvec{f}\) which is equivalent to the joint torque vector \(\:\tau\:={\left({\tau\:}_{1},{\tau\:}_{2},{\tau\:}_{3},{\tau\:}_{4},{\tau\:}_{5},{\tau\:}_{6}\right)}^{T}\) in Eq. (13). Therefore, by combining Eq. (15), we obtain:
Where \(\:D\left(\tau\:\right)\) represents the projection of the joint torque vector in any coordinate system along the three axes; \(\:{\tau\:}_{6x}\) represents the projection of the input torque of the sixth joint along the x-axis direction; \(\:{\tau\:}_{6y}\) represents the projection of the input torque of the sixth joint along the y-axis direction; \(\:{\tau\:}_{6z}\) represents the projection of the input torque of the sixth joint along the z-axis direction. Equation (17) is a non-square matrix, and its rank is equal to the number of the largest linearly independent groups. Therefore, when the joint torque has projection components along the x, y, and z axes in any cartesian coordinate system, \(\:D\left(\tau\:\right)\) is a full-rank matrix.
Prediction and validation of dynamic sensitivity of a robot
Building on the definition and analysis of the dynamic sensitivity coefficient presented in Sect. 2.1, this section explores the analysis, prediction, and validation of the dynamic spatial sensitivity of the ABB IRB 6660 robot at three distinct poses. Initially, the sensitivity of the robot’s structural natural frequency changes is predicted using the modal shapes of its entire structure at these three poses. Subsequently, the changes in natural frequency for each pose are compared to validate the prediction results.
Prediction of the dynamic spatial sensitivity
According to Eq. 10 in Sect. 2.1, the sensitivity of the change in natural frequency is proportional to the structural modal shape. Therefore, the sensitivity of the natural frequency change can be predicted using the structural modal shape. In this section, the natural frequency, damping ratio, and modal shapes of the ABB IRB 6660 − 205 robot structure are identified through impact test modal analysis, as shown in Fig. 1(a). The hammer used in the experiment is PCB 086D05, and its sensitivity is 0.23mV/N. The front-end signal is collected and processed using the LMS SCADAS Mobile SCM2E05 system.
Experimental setup (a) the device (b) measurement points (c) three different poses. Using RobotStudio software (version 6.08.8148.0134 (64-bit), Zurich, Switzerland); https://new.abb.com/products/robotics/software-and-digital/robotstudio.
Figure 1(b) shows the arrangement of structural measurement points for modal identification, 42 measuring points uniformly distributed across the robot. The measurements were performed in batches using DYTRAN 3263A2 acceleration sensor, with 14 three-way sensors used in three measurement batches, and 4 measuring points are arranged in the base, 7 measuring points were arranged on the first joint and connecting rod; A total of 16 measuring points is arranged in the second and third joint and parallel quadrilateral mechanism. The fourth and fifth joints were arranged with 10 measuring points; 5 measuring points were arranged in the sixth joint. At each measuring point, the sensor orientation is aligned with the Cartesian coordinate system on the ground.
Due to the significant variations in joint angles throughout the working space of the six-degree of freedom robotic arm, pose changes not only cause variations in the natural frequency but also leads to changes in the structural modal shapes. Therefore, the entire working space is first divided into regions. Within each region, it is assumed that pose changes have minimal impact on the modal shape variations. However, the modal shapes of the structure change between different regions. Based on this assumption, the working space of the ABB IRB 6660 − 205 robot is divided into three zones, with a central pose point P1, P2, and P3 selected in each region, as shown in Fig. 1(c). The joint angles for the robot at P1 are: 0°, 45°, -10°, 90°, -90°. The joint angles at the P2 pose are: 0°, 0°, 0°, 0°, 0°, 0°. The joint angles at the P3 pose are: 0°, -20°, 25°, -15°, 0°, 0°. Modal shapes of the robot structure at these three poses are obtained through tapping test modal analysis, which are used to predict and compare the sensitivity of natural frequency changes in each region.
The FRFs of the robot structure at three different poses are shown in Fig. 2. Based on these FRFs, the natural frequencies and damping ratios of the first four modes of the robot structure are identified, as shown in Table 1. The modal shapes of the first four modes are shown in Fig. 3. From the comparison of the modal shapes in Fig. 3(a), it is evident that the first mode, the modal shape at the P3 pose is the largest. Therefore, according to the theory in Sect. 2.1, the sensitivity of natural frequency in the corresponding region of P3 is also greater. For the second and the third modes in Fig. 3(b) and (c), the modal shapes for the second and third modes are large at both P2 and P3 poses, so the sensitivities of natural frequency in the regions corresponding to P2 and P3 are greater. For the fourth mode in Fig. 3(d), the modal shape at the P2 pose is the largest, so the sensitivity of natural frequency in the P2 region is greater. Based on this prediction, during the multi-joint combined self-excitation modal analysis, the range of joint motion at the P1 pose region is less restricted, and it’s allowing the angular displacement range to be appropriately enlarged. However, in the regions corresponding to P2 and P3 poses, the joint angle displacement range is more restricted, and the angular displacement range needs to be reduced.
Validation of the dynamic spatial sensitivity
To validate the prediction of natural frequency sensitivity, impact tests were conducted at nine additional poses surrounding the P1, P2, and P3 poses. These nine poses are generated by rotating each joint of the robot by 5°, 10°, and 15° relative to the P1, P2, and P3 poses, respectively. As illustrated in Table 2, P1 is designated as posture 1–1. All joints in posture 1–2 are rotated forward by 5° from P1. Similarly, all joints in posture 1–3 are rotated forward by 10° from P1, and all joints in posture 1–4 are rotated forward by 15° from P1.
P2 is denoted as posture 2 − 1. All joints in posture 2–2 are rotated forward by 5° from P2. All joints in posture 2–3 are rotated forward by 10° from P2, and all joints in posture 2–4 are rotated forward by 15° from P2. P3 is denoted as posture 3 − 1. All joints in posture 3 − 2 are rotated forward by 5° from P3. All joints in posture 3–3 are rotated forward by 10° from P3, and all joints in posture 3–4 are rotated forward by 15° from P3. The specific joint angles corresponding to each pose are detailed in Table 2.
The FRFs from the impact tests at each pose are shown in Figs. 4 and 5, and Fig. 6. The identified modal parameters are presented in Tables 3 and 4, and Table 5. Comparing the FRFs of the four postures around P1 in Fig. 4, the FRF of the robot changes with the joint rotation. Comparing modal parameters of the four postures around P1 in Table 3, the natural frequencies and damping ratios are offset, but the modal order of the entire structure remains unchanged.
According to the identified natural frequencies in Tables 3 and 4, and 5, the sensitivity coefficients of pose-dependent natural frequencies are calculated using the Eq. (1) in Sect. 2.1. The calculated sensitivity coefficients for the first four modes are compared in Fig. 7. From Fig. 7(a), it can be seen that for the natural frequency of the first mode, the sensitivity coefficients in dynamic spatial P3 are the highest, which is consistent with the predicted results in Sect. 3.1. For the second mode in Fig. 7 (b), the largest sensitivity coefficients of natural frequency are in dynamic space P2; For the third mode in Fig. 7 (c), the sensitivity coefficients of natural frequency in dynamic spatial P3 is the highest when the joint rotates by 5°, and the sensitivity coefficient in dynamic spatial P2 are the highest when the joint rotates by 10° and 15°, which is approximately consistent with the predicted results in Sect. 3.1; For the fourth mode in Fig. 7(d), when the joint rotates by 5°, in the P2 dynamic spatial the sensitivity coefficient of natural frequency is the highest, and when the joint rotates by 10° and 15°, sensitivity coefficient in the P3 dynamic spatial is the highest.
To sum up, the method for prediction of the sensitivity of natural frequency based on modal shapes is basically effective. At the same time, according to the prediction results, in the multi-joint self-excited modal analysis, the motion range of the joint in the dynamic spatial P1 is less restricted, and its angular displacement range can be appropriately expanded. However, in the regions corresponding to the P2 and P3, the range of joint angular displacement is greatly limited and needs to be reduced.
Excitation frequency and direction of multi-joint combined motion
The excitation energy and the randomness of excitation direction for multi-joint combined random acceleration and deceleration motion analyzes in this section. The randomness indicator of excitation direction based on the torque projection matrix, is proposed in Sect. 4.1. Section 4.2 discusses of the excitation energy and frequency band of the random inertial forces generated by random acceleration and deceleration movements.
Index of excitation direction randomness
The OMA requires that the direction and energy of the input force exhibit randomness. This section provides the randomness indicator of the input force direction. For the robot structure located in the base coordinate system, assuming the number of input forces is \(\:d\), the input vector composed of the input force vectors is \(\:f={\left({f}_{1},{f}_{2},\cdots\:,{f}_{d}\right)}^{T}\), and the matrix is established as:
In the Eq. (18), \(\:{f}_{dx}\) represents the projection of the input force vector \(\:{f}_{d}\) in the \(\:{x}^{{\prime\:}}\) direction; \(\:{f}_{dy}\) represents the projection of the input force vector \(\:{f}_{d}\) in the \(\:{y}^{{\prime\:}}\) direction; and \(\:{f}_{dz}\) represents the projection of the input force vector \(\:{f}_{d}\) in the \(\:{z}^{{\prime\:}}\) direction. As shown in Fig. 8(a), \(\:x\) \(\:y\) and \(\:z\) represent the base coordinate system; \(\:{x}^{{\prime\:}}\), \(\:{y}^{{\prime\:}}\), and \(\:{z}^{{\prime\:}}\) represent the translated base coordinate system; and \(\:{x}_{i}\), \(\:{y}_{i}\), and \(\:{z}_{i}\) represent the rigid body coordinate system.
According to Eq. (18), when excitation forces act in the same direction on the tested structure, their projection vectors in the matrix are proportional. In this case, only one of the force vectors with the same excitation direction holds meaningful significance, and \(\:D\left(f\right)\) is not a full-rank matrix. Assuming there are \(\:r\) excitation forces acting in repeated directions on the rigid body structure, we obtain:
(a) Projection of the Input Force (b) Not cover all directions (c) Traverse all directions (d) Joint torque direction of six-axis robot. Using RobotStudio software (version 6.08.8148.0134 (64-bit), Zurich, Switzerland); https://new.abb.com/products/robotics/software-and-digital/robotstudio.
According to Eq. (12) and Fig. 8 (b), it can be observed that when the structure is subjected to two linearly independent force vectors, \(\:dim\left[D\left(f\right)\right]=2\), indicating that the two vector directions only form one excitation plane. Whether the structure is sufficiently excited in this case depends on its dynamic characteristics. The input excitation forces might excite the strong response directions required by the various modes of the structure, or fail to cover all directions.
When the structure is subjected to three linearly independent force vectors, as shown in Fig. 8(c), \(\:dim\left[D\left(f\right)\right]=3\), and the matrix columns become full rank. At this point, the excitation forces acting on the structure span all directions in three-dimensional space, which can be considered to meet the directional excitation requirements of all modes. Therefore, \(\:dim\left[D\left(f\right)\right]=3\) can be applied as a sufficient condition for determining the adequacy of the actual excitation direction.
Typically, the motion of the robot is controlled by a joint motor, in which the torsional force of the spindle is related to the power and speed of the motor, while the direction of the output torque of the motor meets the right-hand spiral rule with the rotation direction of the connecting rod. Therefore, when multiple joints of the robot perform acceleration and deceleration movements at the same time, the direction of the joint torque can be simplified as shown in Fig. 8(d). According to the torque projection matrix of Eq. (17) in Sect. 2.2, the sufficient condition that all modes of the robot structure can be excited is \(\:dim\left[D\right(\tau\:\left)\right]\:=3\), that is:
Therefore, excitation of three joints is sufficient to cover the excitation directions within the workspace. However, considering the structural response is also influenced by the excitation position and excitation energy, subsequent experimental validation employs full-joint excitation to ensure that all factors, including energy, position, frequency bands, and direction, are adequately covered.
The application of a single-direction force or torque cannot guarantee sufficient excitation of the robot’s structure and may lead to the omission or absence of certain modes. Controlling multiple joints of the robot to perform inertial motion simultaneously, thereby generating combined impacts in multiple directions, offers a solution to address the issue of excitation direction.
Excitation frequency of multi-joint random movements
In normal robot operation, pulse signals and random signals are two common types of excitation signals. However, pulse signals tend to have relatively low energy within the sampling time and poor signal-to-noise ratios, while random signals are challenging to acquire and difficult to obtain during practical robot operations. Therefore, this paper combines the characteristics of both to use a random pulse signal as a controllable input method. It is assumed that the starting and stopping actions of the robot joints generate inertial excitation forces that affect the entire system. By controlling the joints to produce random inertial impacts, the robot’s overall structure can be excited through the twisting motion of the joints.
The schematic of random acceleration and deceleration movements of a robot is shown in Fig. 9. In Fig. 9(a), a three-dimensional schematic of the robot with small-amplitude random torsion is shown. In Fig. 9(b), the acceleration and deceleration motion law of a single joint is depicted.
The time interval between two adjacent random acceleration and deceleration movements is denoted as \(\:\Delta{t}_{n}\). Previous studies have demonstrated that when robot joints undergo constant acceleration and deceleration movements, they generate inertia impacts similar to square waves33,34,35. Therefore, when the robot joint performs random movements according to the constant acceleration and deceleration rates shown in the upper part of Fig. 9(b), the input force and acceleration will exhibit a rectangular square wave excitation, as illustrated in the lower part of Fig. 9(b). The \(\:\Delta{t}_{n}\) is designed as a pseudo-random sequence to ensure the random motion characteristics within the sampling time, thus generating a smooth frequency band within a certain range.
(a) Single-joint random self-excitation (b) Sequence of random self-excitation motion. Using RobotStudio software (version 6.08.8148.0134 (64-bit), Zurich, Switzerland); https://new.abb.com/products/robotics/software-and-digital/robotstudio.
Numerical simulations were conducted to verify the excitation frequency band. First, random pulse signals with different quantities, denoted as n, were generated. In the three simulations, the number of signals was 1, 8, and 22, respectively. For each simulation, the rectangular pulse duration τ was set to 0.003s; the pulse amplitude was set to 1; the number of sampling points was 1000; and the time intervals between pulses were generated using random numbers.
The power spectrum was computed using the Welch spectral estimation method. The simulation results are shown in Fig. 10. According to the power spectral density curve results in Fig. 10, it can be observed that, within the same sampling time range, as the number of random pulse signals increases, the power spectrum energy increases accordingly.
Validation of multi-joint self-excitation auto modal analysis
Motion range comparison of multi-joint self-excitation
The validation tests for the effectiveness of multi-joint self-excitation modal analysis are conducted on the ABB IRB 6660 − 205/1.9 six-axis serial robot, with a motor power of 3.6 kW, with other specific parameters shown in Table 6. The vibration response is measured using a DYTRAN 3263A2 tri-axial accelerometer, which has a measurable frequency range of 0.3 to 10,000 Hz and a mass of 5.6 g, significantly lower than the overall mass of the robot; thus, the impact of the sensor’s attachment mass is negligible. The structural output data is collected using the front-end signal processing device LMS SCADAS Mobile SCM2E05. The subject and sensors of the multi-joint self-excitation are consistent with those in the hammer test, with a 12 mm diameter four-tooth tungsten carbide milling cutter clamped in place. However, the experiment only requires joint impacts to perform the excitation motion, so the milling cutter is clamped but not used for material cutting. A program segment is written in the RAPID program to control the robot to perform point-to-point acceleration and deceleration motion, where the time intervals for acceleration and deceleration motions are generated randomly within the range of [0, 1].
Based on the robot dynamic sensitivity analysis in Sect. 3, it can be observed that the joint motion range in the P1 posture is less restricted, and the angular displacement range can be increased accordingly. However, in the areas corresponding to P2 and P3 postures, the angular displacement range is more constrained, and it is necessary to reduce the angular displacement range. This section conducts a self-excitation modal analysis experiment considering the motion range for the robot’s P1 and P3 posture areas. For the P1 posture area, where the motion range is less restricted, a large angle displacement self-excitation experiment is conducted by increasing the joint angle by 15°. For the P3 posture area, where the motion range is more restricted, a small angle displacement self-excitation experiment is conducted by increasing the joint angle by 5°. The initial and final postures for the self-excitation modal analysis experiments are shown in Table 7. In the P1 posture area, the initial posture is Posture 1–1, and the final posture is Posture 1–4. In the P3 posture area, the initial posture is Posture 3 − 1, and the final posture is Posture 3 − 2.
The power spectrum of vibration signal is shown in Fig. 11 and the identified modal parameters are shown in Table 8. The cross-power spectrum obtained from self-excited motion in P1 region is shown in Fig.11 (a). The cross-power spectrum obtained from self-excited motion in P3 region is shown in Fig.11 (b).
The identified natural frequencies of the first four modes in the P1 region are 11.1 Hz, 19.4 Hz, 29.3 Hz, and 38.1 Hz, respectively. Compared with the natural frequencies in the impact experiment of posture 1–1, the natural frequency of the second mode varies significantly, with a difference of 2.6 Hz. The changes in the other modes are relatively smaller, with the natural frequency differences all within 1 Hz. The identified natural frequencies of the first four modes in the P3 region are 10.3 Hz, 18.0 Hz, 42.8 Hz, and 50.6 Hz, respectively. Compared with the natural frequencies in the impact experiment of posture 3 − 1, the natural frequency of the fourth mode varies significantly, with a difference of 2.9 Hz. The change in the natural frequency of the first mode is 1.4 Hz. Under the premise of eliminating the influence of pose change on the dynamics, the above changes in natural frequencies are mainly due to the difference in the joint dynamic characteristics between the running state and the static state.
Comparison with multi-joint and single-joint excitation
This section compares and validates the effect of multi-joint movements on the excitation response, this section presents a set of experiments to compare multi-joint combined excitation with single-joint excitation. To ensure the input energy and direction fully excite the robot’s structural dynamics, all six joints are subject to random self-excitation motions in the multi-joint excitation experiment, ensuring that the matrix in Eq. (20) remains full rank. The test subject is the ABB IRB 6660 six-axis serial robot. Fourteen three-axis accelerometers are arranged on the robot’s structural body, and a RAPID program written in Robot Studio is used to control the robot to perform two types of movements: (1) all joints undergo random torsional movements (2) only the sixth joint undergoes random torsional movement.
The angles of all six joints in the initial pose selected for the experiment were 0°. In the first group of experiments, all six joints are simultaneously subjected to a random excitation experiment with a joint angle displacement of 5°. In the second group of experiments, only the sixth joint undergoes a random excitation experiment with a joint angle displacement of 5°. The frequency measurement range is set to 4096 Hz. The comparison of the power spectrum signals between multi-joint and single-joint excitation is shown in Fig. 12.
As shown in Fig. 12, it can be seen that the vibration response amplitude measured during multi-joint excitation reaches a maximum of 1.96e-6, which is significantly higher than the result obtained with single-joint excitation. This indicates that the excitation energy generated by random impacts on all joints (1–6) is much greater than the energy generated by the motion of the sixth joint alone. Therefore, controlling multiple joints of the robot to move can more effectively excite the robot’s structure. Additionally, from the curves in the figure, it can be observed that the frequency response of the robot’s structure is mainly concentrated below 100 Hz. In the frequency range from 150 Hz to 1024 Hz, the response amplitude of the robot’s structure is very weak.
The steady-state diagrams for modal parameters identification are shown in Figs. 13 and 14. Comparing Fig. 13(a) and Fig. 13(b), it can be observed that when the fitting order are 40, the identification results for single-joint self-excitation are poor. The number of unstable poles is large and scattered, and the confidence level of the identification results is low. In contrast, the multi-joint self-excitation identification yields good results, with natural frequencies clearly and neatly distributed, and the number of unstable poles is minimal.
Comparing Fig. 14(a) and Fig. 14(b), it can be seen that when the fitting order are 60, the identification results for single-joint self-excitation contain numerous pseudo-modes. Almost every steady-state frequency line contains numerous unstable points ’V’, indicating severe overfitting. This is a phenomenon of natural frequency migration and merging, making it difficult to accurately identify the natural frequencies and damping ratios. On the other hand, in the multi-joint self-excitation identification process, although there is slight overfitting due to the high order of the fitting equation, the number of unstable poles is very low, and the modal parameters of the structure can be effectively identified.
In summary, when only a single joint of the robot is controlled for idle running, the excitation direction generated by motor torsion is constrained, and the excitation energy produced by random impacts is low, which is insufficient to excite the overall structure of the robot. As a result, the vibration response amplitude at each measurement point on the robot’s body decreases, the signal-to-noise ratio of the collected data deteriorates, and the identification results are poor. Furthermore, compared to the single-joint self-excitation experimental results, when multiple joints are controlled for random self-excitation, the response amplitude of the robot’s structure is increase, and its ability to resist environmental noise and the interference from unstable factors such as algorithmic order is stronger. The pole steady-state plots are more orderly and clearer, enabling the task of identifying the robot’s overall modal parameters can be completed more quickly and effectively.
Conclusions
A method for autonomous modal analysis of robots based on random excitation of multi-joint idle running is proposed. In this method, the dynamic spatial sensitivity analysis is used to limit the range of joint motion. The randomness of the excitation direction is determined based on whether the torque projection matrix is full rank. The random inertial excitation force is generated by the random acceleration and deceleration of multi-joint. The effectiveness of the proposed method is verified through experiments including the spatial sensitivity analysis experiments, multi-joint and single-joint excitation comparison experiment, and autonomous modal analysis experiment considering the range of joint motion. The results of experiments indicate that:
-
(1)
The sensitivity of natural frequency can be predicted by the robot structural modal shapes, thereby obtaining motion range of robot operational modal analysis under pose changes.
-
(2)
Compared with the results of the single joint self-excited experiment, when multiple joints are excited by random inertia force, the pole steady state diagram of the identification algorithm is clearer and more orderly. The identification of robot modal parameters is more effectively achieved.
-
(3)
On the basis of considering the motion range of the robot joint and the randomness of the input signal, the identified modal parameters of the robot operating state have certain differences compared to the stationary state. The modal parameters identified by the operational modal analysis considering the preconditions are closer to the actual operating state.
Data availability
Data is provided within the manuscript.
References
Verl, A. et al. Robots in machining. CIRP Ann. 68 (2), 799–822. https://doi.org/10.1016/j.cirp.2019.05.009 (2019).
Zerun, Z. et al. High precision and efficiency robotic milling of complex parts: challenges, approaches and trends. Chin. J. Aeronaut. 35 (2), 22–26. https://doi.org/10.1016/j.cja.2020.12.030 (2022).
Tsialiamanis, G. et al. On the application of generative adversarial networks for nonlinear modal analysis. Mech. Syst. Signal Process. 166, 108473. https://doi.org/10.1016/j.ymssp.2021.108473 (2022).
Ji, W., Wang, L. Industrial Robotic Machining: A Review. Int. J. Adv. Manuf. Technol. 103 1239–1255, https://doi.org/10.1007/s00170-019-03403-z. (2019).
Mousavi, S. et al. Dynamic modeling and stability prediction in robotic machining. Int. J. Adv. Manuf. Technol. 88 (9), 3053–3065. https://doi.org/10.1007/s00170-016-8938-0 (2017).
Mousavi, S. et al. Stability optimization in robotic milling through the control of functional redundancies, robotics and Computer-Integrated manufacturing. 50 181–192. https://doi.org/10.1016/j.rcim.2017.09.004 (2018).
Huynh, H. N. et al. Modelling the dynamics of industrial robots for milling operations. Robot. Comput. Integr. Manuf. 61, 101852. https://doi.org/10.1016/j.rcim.2019.101852 (2020).
Huynh, H. N. et al. Direct method for updating flexible multibody systems applied to a milling robot. Rob. Computer- Integr. Manuf. 68, 102049. https://doi.org/10.1016/j.rcim.2020.102049 (2021).
Do, T. T., Vu, V. H. & Liu, Z. Linearization of dynamic equations for vibration and modal analysis of flexible joint manipulators. Mech. Mach. Theory. 167, 104516. https://doi.org/10.1016/j.mechmachtheory.2021.104516 (2022).
Mejri, S. et al. Dynamic characterization of machining robot and stability analysis. Int. J. Adv. Manuf. Technol. 82 (1), 351–359. https://doi.org/10.1007/s00170-015-7336-3 (2016).
Karim, A. et al. Analysis of the dynamic behavior of a six-axis industrial robot within the entire workspace in respect of machining tasks. In: IEEE International Conference on Advanced Intelligent Mechatronics, 2017, pp. 670–675. https://doi.org/10.1109/AIM.2017.8014094 (2017).
Chen, C. et al. Rapid prediction of posture-dependent FRF of the tool tip in robotic milling, robotics and Computer-Integrated manufacturing. 64 101906. https://doi.org/10.1016/j.rcim.2019.101906 (2020).
Chen, C. et al. Posture-dependent stability prediction of a milling industrial robot based on inverse distance weighted method. Procedia Manuf. 17, 993–1000. https://doi.org/10.1016/j.promfg.2018.10.104 (2018).
Nguyen, V., Cvitanic, T. & Melkote, S. Data-driven modeling of the modal properties of a 6-DOF industrial robot and its application to robotic milling. J. Manuf. Sci. Eng. 141 (12), 1–24. https://doi.org/10.1115/1.4045175 (2019).
Tunc, L. T. & Stoddart, D. Tool path pattern and feed direction selection in robotic milling for increased chatter-free material removal rate. Int. J. Adv. Manuf. Technol. 89 (9), 2907–2918. https://doi.org/10.1007/s00170-016-9896-2 (2017).
Wang, R. et al. Prediction of pose-dependent modal properties and stability limits in robotic ball-end milling. Robot. Comput. Integr. Manuf. 75, 102307. https://doi.org/10.1016/j.rcim.2021.102307 (2022).
Lei, Y., Hou, T. & Ding, Y. Prediction of the posture-dependent tool tip dynamics in robotic milling based on multi-task Gaussian process regressions. Robot. Comput. Integr. Manuf. 81, 102508. https://doi.org/10.1016/j.rcim.2022.102508 (2023).
Tunc, L. T. & Gonul, B. Effect of quasi-static motion on the dynamics and stability of robotic milling. CIRP Annals - Manuf. Technol. 70 (1), 305–308. https://doi.org/10.1016/j.cirp.2021.04.077 (2021).
Liu, Y. et al. Sparse identification for ball-screw drives considering position-dependent dynamics and nonlinear friction. Robot. Comput. Integr. Manuf. 81, 102486. https://doi.org/10.1016/j.rcim.2022.102486 (2023).
Tunc, L. T. & Shaw, J. Experimental study on investigation of dynamics of hexapod robot for mobile machining. Int. J. Adv. Manuf. Technol. 84 (5), 817–830. https://doi.org/10.1007/s00170-015-7600-6 (2016).
Mohammadi, Y. & Ahmadi, K. Structural nonlinearity of robotic machining systems. Int. Manuf. Sci. Eng. Conf. 2, V002T09A009. https://doi.org/10.1115/MSEC2020-8452 (2020).
Mohammadi, Y. & Ahmadi, K. Single degree-of-freedom modeling of the nonlinear vibration response of a machining robot. J. Manuf. Sci. Eng. 143 (5), 051003. https://doi.org/10.1115/1.4048513 (2021).
Mohammadi, Y. & Ahmadi, K. Chatter in milling with robots with structural nonlinearity. Mech. Syst. Signal Process. 167, 108523. https://doi.org/10.1016/j.ymssp.2021.108523 (2022).
Mokdad, F. et al. Online modal analysis of a flexible robot during grinding, 4th International Operational Modal Analysis Conference. 1 2. (2011).
Maamar, A. et al. Modal identification of a machine tool structure during machining operations. Int. J. Adv. Manuf. Technol. 102 (1), 253–264. https://doi.org/10.1007/s00170-018-3172-6 (2019).
Maamar, A. et al. Pose-dependent modal behavior of a milling robot in service. Int. J. Adv. Manuf. Technol. 107 (1), 527–533. https://doi.org/10.1007/s00170-018-3172-6 (2020).
Nguyen, V. & Melkote, S. N. Identification of industrial robot frequency response function for robotic milling using operational modal analysis. Procedia Manuf. 48, 154–158. https://doi.org/10.1016/j.promfg.2020.05.032 (2020).
Nguyen, V. & Melkote, S. N. Hybrid statistical modelling of the frequency response function of industrial robots. Robot. Comput. Integr. Manuf. 70, 102134. https://doi.org/10.1016/j.rcim.2021.102134 (2021).
Deng, K. et al. Prediction of in-process frequency response function and chatter stability considering pose and feedrate in robotic milling. Robot. Comput. Integr. Manuf. 82, 102548. https://doi.org/10.1016/j.rcim.2023.102548 (2023).
Ge, X. et al. Removal of AM-FM harmonics using VMD technology for operational modal analysis of milling robot. Mech. Syst. Signal Process. 200, 110475. https://doi.org/10.1016/j.ymssp.2023.110475 (2023).
Chen, W. et al. A method to distinguish harmonic frequencies and remove the harmonic effect in operational modal analysis of rotating structures. Mech. Syst. Signal Process. 161, 107928. https://doi.org/10.1016/j.ymssp.2021.107928 (2021).
Daems, P. J. et al. Removal of non-stationary harmonics for operational modal analysis in time and frequency domain. Mech. Syst. Signal Process. 165, 10823. https://doi.org/10.1016/j.ymssp.2021.108329 (2022).
Peng, Y. et al. Characterization and suppression of cutting vibration under the coupling effect of varied cutting excitations and position-dependent dynamics. J. Sound Vib. 463, 114974. https://doi.org/10.1016/j.jsv.2019.114974 (2019).
Peng, Y. et al. Partition of the workspace for machine tool based on position-dependent modal energy distribution and clustering algorithm. Int. J. Adv. Manuf. Technol. 108 (9), 943–955. https://doi.org/10.1007/s00170-020-05487-4 (2020).
Qiu, C. et al. Semi-supervised graph convolutional network to predict position-and speed-dependent tool tip dynamics with limited labeled data. Mech. Syst. Signal Process. 164, 108225. https://doi.org/10.1016/j.ymssp.2021.108225 (2022).
Acknowledgements
This work is supported in part by the National Science Foundation of China (No.52205536), the Hubei Key Research and Development Plan for Technological Innovation (2023BAB071), the Graduate Innovative Fund of Wuhan Institute of Technology (No. CX2023236).
Author information
Authors and Affiliations
Contributions
Y.J.: Writing-original draft, data curation; X.C.: Supervision, Project administration; Y. P.: Methodology, Investigation, Writing-review & editing; X. M.: Methodology, Supervision, Project administration; Q. G.: Formal analysis , data curation; All authors reviewed the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Jiao, Y., Chen, X., Peng, Y. et al. Autonomous modal analysis method for industrial robots considering dynamic spatial sensitivity and excitation randomness. Sci Rep 15, 12581 (2025). https://doi.org/10.1038/s41598-025-95339-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-025-95339-6