Introduction

With the continuous development of geographic information three-dimensional visualization technology and the increasing popularity of UAV remote sensing technology, three-dimensional scene reconstruction based on UAV remote sensing images has shown a pivotal position in the field of geographic information applications. The image acquisition equipment carried by UAVs can efficiently acquire large-scale and high-resolution data, and combined with high-performance computer graphics processing unit and rendering technology, it can realize rapid and high-precision 3D reconstruction of the natural environment, buildings and other targets on the earth.

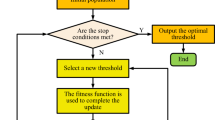
In the past decades, 3D dense reconstruction algorithms have been continuously optimized and updated, and many excellent works have been published in various fields1,2,3,4,5,6,7. Popular computer vision-based dense reconstruction algorithms mostly adopt the framework of PatchMatch MVS6, which can realize parallel processing with the help of GPUs when performing global search, and the algorithm convergence speed is greatly improved, which improves the efficiency and quality of the depth map estimation. PatchMatch MVS usually consists of four steps: random initialization, hypothesis propagation, multi-view matching cost evaluation and hypothesis optimization (as shown in Fig. 1), the last three steps generally require multiple iterations to finally output the depth map and normal map of the current reference frame, based on which the depth maps generated from multi-frame images can eventually be fused into a dense point cloud. The representative algorithms in the industry include: COLMAP8, ACMMP9 and so on. However, the effect of COLMAP algorithm is not ideal enough in dealing with specific tasks, and still need to be improved in the reconstruction of weak texture regions. ACMMP has excellent dense reconstruction effect in indoor scenes with the help of multi-scale geometric consistency guidance and planar prior assistance, which effectively improves the reconstruction effect of weak texture regions, but how to apply it to outdoor scenes under the viewpoint of UAV needs to be further studied.

For 3D reconstruction of UAV images, most of the existing algorithms have problems such as holes in weak texture regions and lack of details of complex models due to the insufficient number of reconstructed scene space points. To address these challenges, we study the related theories and algorithms of MVS based on patch matching, and propose a UAV remote sensing image reconstruction algorithm based on adaptive propagation and multi-region refinement, named APMRR-MVS, which realizes the efficient processing of weak texture, large-scale and complex UAV images.

Based on the commonality of images captured by UAVs and the characteristics of the main application scenarios, our main contribution is to optimize the propagation and refinement aspects of the ACMMP algorithm (as shown in Fig. 1, the red letter modules):

  • Adaptive propagation. In the strategy of selecting hypothesis sampling, it is extended from a fixed checkerboard grid region to a more active adaptive extension region. In contrast to fixed pixel positions and regions, the algorithm diverges towards a specific direction in the neighborhood, selecting pixels with better solutions as the next direction for propagation. This novel strategy significantly increases the likelihood of detecting and acquiring optimal hypothesis samples.

  • Multi-region refinement. In the step of perturbation refinement of the hypothesis, the proposed algorithm achieves more specific solution space exploration by randomly expanding out several local regions. This approach increases the exploration of the solution space of several other local regions on the basis of guaranteeing the exploration in the vicinity of the original hypothesis, which improves the probability of obtaining the optimal solution. In addition, the exploration based on multiple mutually independent local regions can reduce the possibility of local optimality.

Fig. 1
figure 1

Structure of the PatchMatch MVS algorithm. The inputs are UAV remote sensing images and their corresponding camera poses, and the outputs are depth maps and normal maps. The core of PatchMatch MVS contains four steps. Except for the first step, the last three steps generally need several iterations to realize the convergence. The optimization in this paper mainly focuses on the steps of propagation and refinement, see the red marked module in the figure.

Full size image

The improvements of the algorithm can improve the depth estimation accuracy and completeness of weakly textured regions in dense reconstruction, enhance the smoothness of the surface of the reconstructed object, recover a larger number of spatial points, reduce holes, and preserve more texture details.

Related works

PatchMatch MVS

3D reconstruction is mainly categorized into sparse and dense reconstruction, and our work focuses on algorithms related to dense reconstruction in this paper. According to the different ways of representing the spatial model, it can be generally categorized into four types of methods. The first one is voxel-based methods10,11,12, which represent the scene as a 3D voxel grid, with each voxel containing depth information. This method is suitable for simple geometric scene, but it is generally difficult to be used for large-scale 3D reconstruction due to the limitations of the resolution of the voxel grid and the limited storage space. The next method is based on surface evolution13,14,15, which relies on a functional representation of the evolution process to fit the scene surface through iterative optimization. However, this method requires good initial solutions and can be challenging when dealing with complex geometries. The third method is based on image blocks1,3,16, which represents the scene as a set of localized feature blocks or image blocks and infers depth and geometric information by matching similarities between these blocks. Although this method can achieve dense reconstruction by matching key points, it is susceptible to illumination, noise and occlusion. Finally, depth map-based methods2,7,8 work by estimating the depth map of each image and then fusing them into a large-scale, consistent representation of the 3D scene. In this paper, we choose the depth map-based method to accomplish the UAV remote sensing image dense reconstruction by using the PatchMatch MVS method with high efficiency and performance for depth map estimation. The PatchMatch method was originally developed by Barnes et al.17. Its main goal is to quickly identify the approximate nearest neighbors between patches of two images. Shen et al.6 extended the PatchMatch idea to multi-view stereo. The principle of PatchMatch MVS is based on two key observations: first, neighboring pixels are highly correlated with each other, and second, geometrically neighboring pixels maintain their relative positions from different viewpoint. Based on these observations, PatchMatch MVS estimates the 3D geometry of a scene by quickly searching for the best pixel correspondences between different views.

In the propagation step of the PatchMatch MVS algorithm, researchers have tried a number of different approaches in order to improve the efficiency and accuracy of depth map estimation. Among them7,8,18,19, used a sequential propagation scheme to improve the efficiency of the algorithm to a certain extent by alternating vertical and horizontal propagation operations in the iterations of the algorithm, but there are some limitations in the search direction. Wei et al.19 instead used scan lines (one-eighth of the height or width of the image) to guide the propagation to improve the parallelism of the algorithm, but was limited by the number of rows or columns of image pixels. Subsequently, Galliani et al.2 proposed a diffusion-like propagation scheme based on a checkerboard grid, where the search space resembles the arrangement of red and black chess pieces, which improves the updating efficiency of hypothesis sampling, but does not fully reflect the prioritization of hypothesis selection. ACMMP algorithm proposed by Qingshan Xu et al.9 expands fixed points into eight fixed regions and selects the best hypotheses in each region for propagation sampling, which maintains high efficiency and takes into account the sampling of excellent hypotheses in the surrounding regions, but the sampling method of excellent hypotheses at the far end still needs to be improved.

When calculating the multi-view matching cost, the most critical thing is to select the view subset correctly, because the wrongly selected views can lead to a large error in the matching cost. To address this challenge, many researchers have tried lots of methods to improve the accuracy of view selection. In a diffusion-like propagation scheme, Galliani et al.2 select a fixed number of views with minimum k-matching cost, the value of k depends on different factors. In general, taking a higher value of k increases the redundancy and improves the accuracy of the 3D points, but there is also a risk of mismatch, which reduces the robustness. In the sequential propagation scheme18,19, attempts to perform view selection only from a global perspective, ignoring the differentiation of visibility between pixels. To address this issue, Zheng et al.7 attempted to construct probabilistic graphical models to jointly estimate depth map and view selection. In addition, SchÖnberger et al.8 introduced geometric prior and time smoothing to better characterize the state transfer probabilities. However, the efficiency of pixel update in the sequential propagation scheme is still a prominent issue. ACMMP9 algorithm chooses to construct a probabilistic graph model to jointly estimate the depth map and view selection in a diffusion-like propagation scheme, which improves the accuracy of the multi-view matching cost computation while taking into account the efficiency of pixel update.

In the refinement step of PatchMatch MVS, the earliest strategy was to add perturbation to the original hypothesis and find a better hypothesis by comparing it with the perturbed one. The approach, while capable of exploring the solution space to some extent, is limited to the solution space in the neighborhood of the original hypothesis. The refinement stage of COLMAP8 involves permutations and combinations of the original hypothesis, random hypothesis, and perturbed hypothesis, and introduces hypothesis information sampled during the hypothesis propagation phase to form a hypothesis set. The hypothesis with the lowest matching cost is then updated as the current hypothesis for the target pixel. This strategy expands the exploration range of the solution space to some extent, but it is still constrained by the position of the original hypothesis within the solution space. The refinement strategy of ACMMP9 is similar to that of COLMAP, with the key difference being that ACMMP does not introduce hypothesis sampling from the hypothesis propagation phase into its hypothesis set. However, due to differences in the overall algorithmic structure, this does not affect ACMMP’s optimization effectiveness for the target pixel hypothesis. Like COLMAP, ACMMP is also limited by the position of the original hypothesis in the solution space, resulting in a relatively low degree of exploration of the solution space.

Typical works

COLMAP

COLMAP8 is an algorithm that utilizes probabilistic graphical models to jointly estimate depth values, normal information and view selection, achieving highly accurate depth estimation. Its main idea is as follows: initially, hypotheses are made for all pixels in the reference image through random initialization. Then, a sequential propagation scheme scans the images in a chain pattern (as shown in Fig. 2), where the estimation of the current pixel is updated based on the estimations of previous pixels in the propagation direction. Subsequently, a probabilistic graphical model is constructed to calculate the joint probability, where the similarity of image patches is measured using bilateral weighted normalized cross-correlation and modeled as a likelihood function, and the smooth prior of view selection is modeled through a state transition matrix. COLMAP employs the generalized expectation maximization algorithm to infer the weights of different source images, guiding the weighted multi-view matching cost and selecting the hypothesis with the minimum weighted cost as the current best estimate. Afterwards, COLMAP generates a small number of additional hypotheses to refine previous estimates by combining random perturbations of depth values with the current best normal information, and vice versa, finally gets the matching cost. The algorithm achieves convergence through the iteration of last three steps. Although COLMAP performs well in some small-scale scenarios, its reconstruction results are not ideal when dealing with scenes with many weak texture regions or of large-scale size.

Fig. 2
figure 2

Sequential propagation scheme. Circles representing pixels in the image.

Full size image

ACMMP

ACMMP9 is an algorithm that jointly estimates depth values, normal information, and view selection through a probabilistic graphical model, and enhances the reconstruction quality through multi-scale geometric consistency guidance and planar prior assistance, which can realize high-precision and high-completeness dense reconstruction. Firstly, ACMMP randomly initializes all the pixels in the reference image with initialization assumptions. Subsequently, based on Gipuma’s2 propagation design (as shown in Fig. 3a), ACMMP designed a new sampling method on the checkerboard area(as shown in Fig. 3b), setting 4 V-shaped regions and 4 long-stripe regions, each V-shaped region contains 7 samples and each long-stripe region contains 11 samples, which can be selected to take into account more samples in more directions and increase the possibility of finding better hypotheses. Secondly, the matching cost weights of all source views for the target pixel in the reference view are jointly estimated by constructing a probabilistic graphical model, and a rewarding mechanism is introduced for pixels that are in the same object plane to make their multi-view matching cost weights converge. Next, a perturbation is added to the original hypothesis to generate a perturbation hypothesis and a new hypothesis is randomly generated, then the elements of the original, perturbation, and random hypotheses are permutated and combined, which is used by ACMMP to generate an additional set of hypotheses and compute the matching cost. The algorithm achieves convergence through the iteration of last three steps. In addition, ACMMP has two strategies for optimizing the depth estimation of weakly textured regions. One of them is multiscale geometric consistency guidance20 which propagates back reliable estimates obtained from down-sampling through image layering for fusion and optimizes the results by geometric consistency constraints; and the second is planar prior assistance21 which obtains planar priori information about weakly textured regions by triangulating the sparse points extracted from the depth map and uses it to guide subsequent depth map estimation. While the meticulous algorithm design of ACMMP enables it to achieve commendable reconstruction in various environments, there remains room for improvement in the reconstruction of regions with weak texture, and the accuracy of spatial point recovery also requires enhancement.

Fig. 3
figure 3

(a) Symmetric checkerboard propagation; (b) Adaptive checkerboard propagation. Circles represent pixels in the image, light blue areas represent sampling regions, and solid red circles represent sampling points.

Full size image

Learning-based shape reconstruction

The great success of deep neural networks in the computer field has triggered people’s interest in introducing learning into other directions, for example, in the image field such as target detection22 and semantic segmentation23, which have also achieved very excellent results in recent years, meanwhile, the 3D reconstruction technology of UAV scenes based on deep learning is also developing rapidly, Liu et al.24 constructed a large-scale synthetic multi-view oblique aerial image dataset (WHU-OMVS dataset), and proposed a 3D real scene reconstruction framework that can efficiently process large-capacity aerial images with large depth variations, named Deep3D; Tong et al.25 proposed for the first time the introduction of a GAN-based adversarial training end-to-end deep inference model in the MVS domain, which is an effective complement to self-supervised scene reconstruction; Wei Zhang et al.26 proposed the AggrMVS algorithm, which enhances visual consistency to address the lack of accuracy due to the characteristics of aerial image data, and reconstructs a multicategory synthetic aerial scene benchmark dataset from a generic MVS dataset. In addition to this, to promote the research of deep learning-based 3D reconstruction techniques for UAV scenes, Xiaoyi Zhang et al.27 proposed the first stereo matching dataset UAVstereo for UAV low-altitude scenes; Li et al.28 proposed a deep learning framework for remote sensing image registration by predicting the probability of semantic spatial location distribution, which ensures the improved speed of remote sensing image analysis and pipeline processing while facilitating novel directions in learning-based registration. And the combination of deep learning-based UAV scene 3D reconstruction technology with practical applications is getting closer and closer, Ling et al.29 designed an improved multi-view stereo structure based on the combination of remote sensing and artificial intelligence, which can realize the accurate reconstruction of jujube tree trunks in order to enhance the efficiency of agricultural work. Deep learning-based 3D reconstruction technology for UAV scenes shows great potential in many fields, enabling efficient and accurate 3D modeling. Deep learning-based 3D reconstruction techniques for UAV scenes show great potential for efficient and accurate 3D modeling in many fields. However, it also faces challenges such as high computational requirements, data quality and environment dependency.

Technical details

Random initialization

During random initialization, we adopt the same approach as described in2, randomly generating a hypothesis \(\:\theta \: = [n^{T} ,d]^{T}\) for each pixel in the reference image \(\:{I}_{ref}\) to construct a 3D plane, where \(\:d\) represents the distance from the origin to the 3D plane, and \(\:n\) denotes the normal vector corresponding to the 3D plane. For each hypothesis, the matching cost is computed from up to \(\:N-1\) source views using homography mapping30. Specifically, given the camera parameters of the reference image \(\:{I}_{ref}\) as \(\:{P}_{ref}={K}_{ref}\left[I\right|0]\), and the camera parameters of the \(\:j\)-th source view as \(\:{P}_{j}={K}_{j}\left[{R}_{j}\right|{t}_{j}]\), the homography computation between them is given by:

$$\:{H}_{j}={K}_{j}\left({R}_{j}-{t}_{j}\frac{{n}^{T}}{d}\right){K}_{ref}^{-1},$$
(1)

Using the homography transformation, we can obtain corresponding pixel patches from the reference image \(\:{I}_{ref}\) to the \(\:j\)-th source image and compute their matching cost using a bilateral-weighted adaptive algorithm based on Normalized Cross-Correlation (NCC)8.

Propagation

Indeed, empirical evidence suggests that pixels in close proximity to the target pixel are more likely to yield superior hypotheses. Building upon the algorithm proposed in9, we have retained the four V-shaped sampling regions surrounding the target pixel. However, in our extended sampling strategy, we adopt a more proactive approach to exploration (as shown in Fig. 4). This involves actively selecting more optimal solutions iteratively to investigate distant hypotheses.

Fig. 4
figure 4

Selective checkerboard propagation. Circles represent pixels in the image, light blue areas represent sampling regions, light blue arrows represent directions in which sampling regions are likely to expand, and solid red circles represent sampling points.

Full size image

The specific implementation algorithm is outlined as follows.

Algorithm 1
figure a

Adaptive propagation of sampling strategies for distal regions.

Full size image

In Algorithm 1, the labelled pixel refers to the hypotheses pixel in the region with the lowest multi-view matching cost. The input is the initial labelled pixel, which is set to be start pixel in the distal region. The output is the hypotheses coordinates of the pixel with the lowest multi-view matching cost within the explored region. The specific implementation of the algorithm is to start from the input pixel, by comparing the assumed multi-view matching costs of two neighboring pixels in the corresponding directions on the checkerboard grid, selecting the hypotheses pixel with the lower multi-view matching cost as the direction of the next region propagation until the boundary of the region propagation is reached, comparing the multi-view matching costs of all hypotheses pixels in the region and outputting the coordinates of the hypotheses coordinates of the pixel with the lowest multi-view matching cost. When the matching costs of two neighboring pixel hypotheses are equal, we tend to expand in a clockwise direction (the region above the target pixel expands to the right, the region to the right expands downward, and so on) to avoid inter-region encounters.

From the global view, the selective regions will spread outward in \(\:X\) rows (columns), and the regional optimums are selected by comparing the multi-view matching cost of each pixel within each region in the previous iteration of the algorithm. The regional optimums of the eight regions together form a sampled combination of hypothesis propagation in the same view, which can be used in the subsequent estimation of the multi-view matching cost, and the excellent hypotheses will be reflected in the process to realize the hypothesis propagation within the same view.

With such a strategy, the sampling region is adaptively selected according to the plane situation, better exploring the hypothesis of pixels in the same plane as the target pixel, increasing the likelihood that a better solution will be sampled while trying to avoid being trapped in a local optimum.

Multi-view matching cost evaluation

The ACMMP9 algorithm has excellent applicability and accuracy in the design of multi view matching cost evaluation, and our algorithm also adopts the same method in this section.

The visibility function denotes the visibility of pixel \(\:p\) on the source view \(\:{I}_{j}\) as \(\:{Z}^{j}\), while the visibility of its neighboring pixels is denoted as \(\:{Z}_{n}^{j}\). The candidate hypothesis set is denoted as \(\:{\Theta\:}={\left\{{\theta\:}_{i}\right\}}_{i=0}^{8}\), comprising the current hypothesis and eight hypotheses obtained through same-view propagation sampling. The patch corresponding to pixel \(\:p\) on the reference image is denoted as\(\:\:{X}^{ref}\), and the corresponding patch observed on the source view \(\:{I}_{j}\) via \(\:{\Theta\:}\) is\(\:{\:X}^{j}={\left\{{X}_{i}^{j}\right\}}_{i=0}^{8}\). Following this rationale, the joint probability can be expressed as:

$$\:P\left({X}^{j},{Z}^{j},{\Theta\:},{Z}_{n}^{j}\right)\propto\:P\left({X}^{j}|{Z}^{j},{\Theta\:}\right)P\left({Z}^{j}|{Z}_{n}^{j}\right)$$
(2)

where \(\:\left({X}^{j}|{Z}^{j},{\Theta\:}\right)=\sum\:_{i=0}^{8}P\left({X}_{i}^{j}|{Z}^{j},{\theta\:}_{i}\right)\), each hypothesis is modeled independently from the source view. There is also a smoothness incentive model for neighboring pixels:

$$\:P\left({Z}^{j}|{Z}_{n}^{j}\right)=\sum\:_{{p}^{{\prime\:}}\in\:\mathcal{N}\left(p\right)}P\left({Z}^{j}|{Z}_{{p}^{{\prime\:}}}^{j}\right)$$
(3)

where \(\:\mathcal{N}\left(p\right)\) represents the four surrounding neighboring pixels. \(\:P\left({X}_{i}^{j}|{Z}^{j},{\theta\:}_{i}\right)\) is modeled by a Gaussian function as:

$$\:P\left({X}_{i}^{j}|{Z}^{j},{\theta\:}_{i}\right)={e}^{-\frac{{m}_{i,j}^{2}}{2{\sigma\:}^{2}}}$$
(4)

where \(\:\sigma\:\) is a constant, and \(\:{m}_{i,j}\) represents the matching cost of this pixel from the reference view \(\:i\) to the source view \(\:j\) calculated under the bilateral weighted algorithm. \(\:P\left({Z}^{j}|{Z}_{{p}^{{\prime\:}}}^{j}\right)\) represents the transition probability:

$$\:P\left({Z}^{j}|{Z}_{{p}^{{\prime\:}}}^{j}\right)=\left\{\begin{array}{c}\eta\:,\:\:\:if\:{Z}_{p}^{j}={Z}_{{p}^{{\prime\:}}}^{j}\\\:1-\eta\:,\:\:\:\:\:\:else\end{array}\right.\:$$
(5)

When setting \(\:\eta\:\) to a larger value, the view selection consistency of neighboring pixels in the same object plane will be improved.

According to Bayes’ theorem, a pixel \(\:p\) in the source view \(\:{I}_{j}\) is selected with probability:

$$\:P\left({{Z}^{j}|X}^{j},{\Theta\:},{Z}_{n}^{j}\right)\propto\:P\left({X}^{j}|{Z}^{j},{\Theta\:}\right)P\left({Z}^{j}|{Z}_{n}^{j}\right)$$
(6)

Building upon the aforementioned view selection probability, weights \(\:{\omega\:}_{j}\) are defined for each source view \(\:{I}_{j}\) using Monte Carlo sampling31. In this context, the multi-view matching cost for pixel \(\:p\) in the reference view under hypothesis \(\:{\theta\:}_{i}\) is defined as follows (the current best hypothesis for pixel \(\:p\) is updated by the hypothesis with the minimum multi-view matching cost):

$$\:{m}_{photo}\left(p,{\theta\:}_{i}\right)=\frac{\sum\:_{j=1}^{N-1}{\omega\:}_{j}\bullet\:{m}_{i,j}}{\sum\:_{j=1}^{N-1}{\omega\:}_{j}}$$
(7)

Refinement

In order to further improve the efficiency of exploring the solution space and reduce the probability of falling into local optima, we design a novel strategy that can explore the solution space more efficiently, focusing on the exploration efficiency for other solution space regions. We generate \(\:N-1\) random hypotheses in each refinement step, and then generate \(\:Y\) perturbation hypotheses for each of the total \(\:N\) hypotheses containing the original hypothesis and the random hypotheses, as shown in Fig. 5.

Fig. 5
figure 5

Hypothesis distribution in multi-region refinement. Blue circles represent original hypotheses, red circles represent random hypotheses and green circles represent perturbed hypotheses.

Full size image

Centered on each initial point (nodes in left column in Fig. 5), a number of mutually independent regions are formed, from which to start the exploration of the solution space. The details are shown in Algorithm 2.

Algorithm 2
figure b

Multi-region refinement strategy.

Full size image

In algorithm 2, \(\:{\theta\:}_{cur}\) denotes the original hypothesis, \(\:{m}_{photo}\left(p,{\theta\:}_{cur}\right)\) denotes the multi-view matching cost of \(\:{\theta\:}_{cur}\) at pixel\(\:\:p\); \(\:{\theta\:}_{rnd}\) signifies the randomly generated hypothesis, \(\:{\theta\:}_{prt}\) denotes the perturbed hypothesis, \(\:{m}_{photo}\left(p,{\theta\:}_{prt}\right)\) representing the multi-view matching cost of \(\:{\theta\:}_{prt}\) at pixel \(\:p\); \(\:{\theta\:}_{best}\) is the optimal hypothesis with the lowest multi-view matching cost, initially set as \(\:{\theta\:}_{cur}\), \(\:{m}_{photo}\left(p,{\theta\:}_{best}\right)\) denotes the multi-view matching cost of \(\:{\theta\:}_{best}\) at pixel \(\:p\), initially set as \(\:{m}_{photo}\left(p,{\theta\:}_{cur}\right)\).

The inputs of the algorithm are the original hypothesis and its multi-view matching cost, and the outputs are the hypothesis with the lowest multi-view matching cost in all regions and its multi-view matching cost. Specifically, we construct a number of independent regions centered on the initial points (original and perturbed hypotheses) and explore the better hypotheses in the solution space through the distribution points (perturbed hypotheses) within each region, and finally traverse the distribution points within all regions to update the optimal hypotheses as well as the lowest multi-view matching cost in this refinement session.

The perturbation hypotheses are generated as:

$$\:{\theta\:}_{depth}^{prt}=\left[1+R\left(-1,1\right){\rm\:P}\right]{\theta\:}_{depth},$$
(8)

where \(\:{\theta\:}_{depth}^{prt}\) is the depth value in the perturbation hypothesis, and \(\:R\left(-1,1\right)\) is a random number between − 1 and 1, and \(\:{\rm\:P}\) is the perturbation coefficient. \(\:{\theta\:}_{normal}^{rnd}\) is obtained from the variation of the random rotation matrix generated with the perturbation coefficients \(\:{\rm\:P}\).

The refinement strategy of multi-point distribution reduces the risk of local optimum by exploring regions independently from each other, which further expands the exploration of the overall solution space, improves the exploration efficiency of excellent hypotheses for weakly textured regions. Also the strategy is conducive to improving the accuracy of the point cloud as well as accelerating the convergence of the algorithm.

Point cloud reconstruction

After obtaining all the depth maps, it is necessary to fuse all of them into a whole, i.e. reconstruct them into a dense point cloud. Inspired by32, ACMMP9 algorithm proposes an adaptive fusion approach for depth maps, the same method can be used for 3D reconstruction of UAV remote sensing images in this paper. ACMMP designs a consistency constraint metric, which only utilizes estimates meeting the following constraints: relative depth error should be less than \(\:{\tau\:}_{1}\), angle between normal should be less than \(\:{\tau\:}_{2}\), and reprojection error should be less than \(\:{\tau\:}_{3}\) in at least \(\:{\tau\:}_{4}\) views. The consistency metric for pixel \(\:p\) in image \(\:{I}_{i}\) is defined as follows:

$$\:C\left(p\right)=\sum\:_{j=0\wedge\:j\ne\:i}^{N-1}{C}_{i,j}\left(p\right),$$
(9)
$$C_{{i,j}} \left( p \right) = e^{{ - \left( {\lambda _{d} \,\varepsilon + \lambda _{n} \,\theta + \lambda _{r} \,\varphi } \right)}}$$
(10)

where \(\:{\lambda\:}_{d}\), \(\:{\lambda\:}_{n}\) and \(\:{\lambda\:}_{r}\) represent the weights used to balance the different terms respectively. This means that if the equation can be dynamically chosen the combination of the, \(\:\theta\:\) and \(\:\phi\:\) terms such that \(\:C\left(p\right)>n\bullet\:\tau\:\) holds, then the estimate will be considered reliable. Finally, the reliable estimate will be back-projected into 3D space to generate a point cloud. This fusion method improves the accuracy, completeness and robustness of the point cloud reconstruction.

Experiments

The following experiments were run on a computer with an Intel i5-6300HQ CPU and an NVIDIA GTX 960 M, with specific parameter settings:

$$\:\left\{\sigma\:,\eta\:,X,N,Y,{\tau\:}_{1},{\tau\:}_{2},{\tau\:}_{3},{\tau\:}_{4},{\lambda\:}_{d},{\lambda\:}_{n},{\lambda\:}_{r},\tau\:\right\}=\left\{\text{0.3,0.9,50,3},\text{3,0.01,30}^\circ\:,\text{2,1},\text{200,10,1},0.3\right\}$$

We used COLMAP33 to estimate the camera pose, as well as employing multi-scale geometric consistency guidance and planar prior assistance strategies to optimize the reconstruction results. We will divide the experiment into three parts to explore the performance of our algorithm in various situations, as shown in the Fig. 6.

Fig. 6
figure 6

Experimental process display diagram.

Full size image

Performance testing of algorithms in indoor scenarios

DTU dataset

Danish Technical University (DTU) dataset34 is a depth image dataset used to evaluate and improve 3D reconstruction and depth estimation algorithms. The dataset contains image sequences from different indoor scenes, each containing depth images taken from different viewpoints. In order to simulate the quality of the 3D reconstruction under the tilted camera angles of the UAV, we use images from scan110 and scan114 in the DTU dataset, and only use 15 of them with similar tilt camera angles as the basis in each scene. In addition, we adjusted the image resolution to \(\:1200\times\:900\), to explore the performance of our algorithm at low resolution.

Evaluation on DTU dataset

In a specific process of point cloud evaluation with mean distance metric35, accuracy (Acc.) is the distance from a point in the reconstructed point cloud to the corresponding point in the true value of the point cloud (scanning by the structured light), which reflects the accuracy of the spatial point positions in the reconstructed point cloud. Completeness (Comp.), on the other hand, measures the distance from points in the point cloud ground truth to their nearest counterparts in the reconstructed point cloud, providing insight into the completeness of the reconstructed point cloud. The overall performance is assessed by averaging the accuracy and completeness scores, offering a comprehensive evaluation of the reconstructed point cloud. Lower values for these three metrics indicate better reconstruction quality. The reconstructed point cloud is down-sampled to ensure unbiased evaluation, particularly because regions with rich textures often contain dense 3D points. The evaluation program is provided by the authors of the DTU dataset. We compare CMVS/PMVS, COLMAP and ACMMP to our algorithm. The evaluation results are listed in Table 1.

Table 1 Evaluation results of each algorithm on the DTU dataset.
Full size table

It can be noticed that in this experiment, our algorithm has better performance in all the metrics, the reconstructed point cloud is closer to the groudtruth, more reliably and has better effects under a perspective similar to oblique photography. However, from the test results of running time, our algorithm has better reconstruction results, but at the same time, it also loses part of the running efficiency.

The results of depth map estimation during model reconstruction are shown in Fig. 7. Compared with others, our algorithm generates fewer depth map holes (as shown in the red box in Fig. 7), better depth estimation in weakly textured regions, and fewer cases of locally optimal, which are especially critical to the quality of 3D reconstruction. It is worth mentioning that because the effect of CMVS/PMVS algorithm is not ideal compared with other algorithms in depth map estimation, the results are significantly different, so it is not shown here.

Fig. 7
figure 7

Depth map estimated with different algorithms.

Full size image

The reconstruction results of scan110 and scan114 under four algorithms are shown in Fig. 8, and it can be clearly seen that the number of spatial points reconstructed by our algorithm is the highest. It is reflected in the effect of the model with fewer holes, higher completeness. It is obviously that after adopting the multi-region refinement strategy as well as the adaptive propagation strategy, the reconstruction effect of the weakly textured region improves significantly, as shown in the red box of Fig. 8. Our algorithm shows better results both in the area of the reconstructed model ground and the spatial point density.

Fig. 8
figure 8

Comparison of reconstruction effects of four algorithms in scan110 and scan114 scenarios.

Full size image

Performance testing of algorithms in low altitude drone scenarios

Blended MVS dataset

We used Blended MVS dataset37 in this experiment. Blended MVS dataset Contains 113 dedicatedly selected and reconstructed 3D models. These texture models cover a variety of different scenes including cities, buildings, sculptures and small objects. Each scene contains 20 ~ 1000 images, totaling over 17,000 images. The dataset contains many scenes taken from the perspective of the UAV. We selected part of the images in three scenes as input, and carried out comparison experiments between algorithms on the premise of ensuring the same number of images input.

Evaluation the effect of 3D reconstruction from Drone’s perspective

To be specific, in scene 1, 18 images with a resolution of 1100 × 825 were selected as input, two groups of comparison experiments (a and b) were carried out. In scene 2, we selected 10 images with a resolution of 1300 × 975 as input, and also conducted two groups of comparison experiments (c and d). In Scene 3, we selected two different groups of images as input to reconstruct different perspectives of the building; each group (e or f) contains eight images with a resolution of 1400 × 1050. All the quantization results of three scenes reconstructed with four algorithms are listed in Table 2. Three groups of experimental data show that the algorithm proposed in this paper can reconstruct more space points than others.

Table 2 Number of space points in three scenarios.
Full size table

The reconstruction effect of comparative experiment of each group is shown in Fig. 9. We analyzed and discussed the experimental results from three aspects respectively.

Fig. 9
figure 9

UAV viewpoint scene in the Blended MVS dataset and reconstruction effect with 4 algorithms.

Full size image
Reconstruction effect of weak texture regions

From the experimental results in Fig. 9a,e (shown in red boxes), we can find that the reconstruction effect of ACMMP is better than CMVS/PMVS and COLMAP for the same image input, but the reconstruction of ACMMP still has holes in some weak texture plane regions. The overall reconstruction effect of our algorithm is not weaker than that of ACMMP, but in the weak texture plane region ours is better. It is obviously that the weak texture plane reconstruction with our algorithm is more complete, which is especially important for 3D reconstruction based on UAV images.

Model detail preservation

From the results in Fig. 9b,c (shown in red boxes), we can find that ACMMP retains more texture details than CMVS/PMVS and COLMAP, and the model is relatively a little bit more complete. However, in the case of the same image input, our algorithm shows better results in terms of detail retention, and generates more complete models and better reconstruction results.

Spatial point misestimating

In the Fig. 9d,f (shown in red boxes), it can be found that the models reconstructed by ACMMP have higher spatial point density and are more complete, retaining more texture details, compared to those reconstructed by CMVS/PMVS and COLMAP, but there are some misestimated spatial points mixed in the models. In contrast, the models reconstructed by our algorithm not only have a higher spatial point density than ACMMP, but also have significantly fewer misestimated spatial points and relatively better model completeness and accuracy while retaining more weakly textured planar regions and texture details.

Performance testing of algorithms in larger drone scenarios

Pix4D dataset

Pix4D provides a series of publicly available datasets38 aimed at showcasing the functionality of its image processing and 3D modeling software, and providing users with materials for learning and experimentation. These datasets include high-resolution drone imagery, Light Detection and Ranging (LiDAR) point cloud data, and textured 3D models, covering multiple fields such as architecture, agriculture, urban planning, and environmental monitoring. The following experiment was conducted on a computer equipped with Intel Core i9-9900 K CPU and NVIDIA GeForce RTX 2080 Ti to investigate the performance of the algorithm in high-resolution images of large-scale drone scenes.

Evaluating the effectiveness of 3D reconstruction in large-scale drone scenarios

To be specific, we chose two large UAV scenes for our experiments. The first scene is an urban spatial scene containing 169 images with a resolution of 4608 × 3456, and the second scene is a quarry scene containing 191 images with a resolution of 5472 × 3648. To further explore the performance of our algorithm in large-scale drone scenes, we have incorporated the ACMH20, ACMM20, and ACMP21 algorithms, which are of the same type, into the experiments. The reconstruction results of each group of comparison experiments are shown in Fig. 10.

Fig. 10
figure 10

The reconstruction performance of seven algorithms in two large drone scenarios on the pix4d dataset.

Full size image

In Fig. 10, the second row of each scene shows the portion of the first row of images indicated by the white box. From the macroscopic point of view, CMVS/PMVS, COLMAP, ACMH, ACMM, and ACMP have slightly lower completeness, while our algorithm is almost identical to ACMMP. However, in terms of microscopic details, our algorithm outperforms the other six algorithms, which is reflected in the fact that more texture details are preserved and fewer holes in the model, as shown in the red box in Fig. 10.

Discussion

In this paper, we propose optimization strategies in the Propagation and Refinement sessions of PatchMatch MVS to further improve the reconstruction of dense point clouds.

The optimization strategies we propose in Propagation and Refinement are more efficient in the emergence and propagation of good hypotheses than other algorithms of the same type and reduce the possibility of falling into a local optimum, which is reflected in the reconstruction model by a larger number of spatial points, better preservation of details, more complete reconstruction of the weakly textured regions, and fewer misestimated spatial points, and also better reconstruction results in large UAV scenes. However, the performance of our method still needs to be improved when dealing with the reconstruction of very weak texture regions, such as the vast farmland and dense forests in UAV scenes. Second, the efficiency of the algorithm also needs to be strengthened, and we need to optimize the structure of the algorithm to improve the operation efficiency. In addition, there is still a certain probability of falling into the local optimum, and there is still room for improvement in the accuracy of the model details, which will be a problem that we will continue to address in our subsequent research.

In summary, the optimization strategy proposed in this paper improves the effect of the reconstruction model and achieves a better performance in low altitude and even large UAV scenes, which provides reference material for further research on the application of Multi-View Stereo in the field of UAVs in the future.

Conclusions

In this paper, we propose two optimization strategies on specific aspects of PatchMatch MVS that can further improve the reconstruction results.

In the propagation step, we propose an adaptive propagation strategy based on a checkerboard grid to expand the distal sampling region by continuously selecting pixels with better hypotheses. The strategy allows for more flexible exploration to the far end and improves the quality of sampling the hypotheses of pixels within the same view.

In the refinement step, we propose a multi-region refinement strategy. This strategy involves exploring the solution space surrounding the original hypothesis and several randomly selected hypotheses by distributing several points around each of them. This approach can not only improve the efficiency of exploring better hypotheses, but also reduce the possibility of pixel hypotheses trapping in local optimum through its relatively independent exploration pattern.

In the experiments, first we demonstrate better performance of our method in terms of both accuracy and completeness in the evaluation of the DTU dataset. Second, Comparative experiments in the UAV view direction on the Blended MVS dataset demonstrate that our method performs better in the reconstruction of weakly textured regions, in addition to preserving specific texture details to a greater extent and reducing the erroneous estimation of spatial points. Finally, our algorithm also has better performance in large drone scene reconstruction in Pix4D.