With the rapid acceleration of urbanization, air pollution has emerged as an increasingly critical issue. Prolonged exposure to polluted air markedly increases morbidity and mortality rates, establishing it as a significant contributor to the global burden of disease1. Among various air pollutants, fine particulate matter (PM2.5) represents the most critical and widely acknowledged environmental challenge in China2. PM2.5 can penetrate deep into the respiratory system, compromising lung function and contributing to various diseases, with its adverse effects extensively documented3. Research indicates that exposure to ambient PM2.5 causes more than 4 million premature deaths globally each year4. The implementation of effective measures to mitigate PM2.5 pollution not only enhances public health but also significantly reduces premature mortality rates5.

However, PM2.5 concentration variations are influenced by a multitude of complex factors, including transportation, industrial emissions, and meteorological conditions, making pollution control a highly challenging task. In existing research, scholars have employed various methods to monitor and analyze air pollution. For instance,5 and6 used the LoT model combined with mobile GPRS sensor arrays to monitor the spatial distribution of pollution sources7; applied the STIRPAT model to examine the impact of economic development and energy consumption on air pollution8 used statistical data analysis to identify the causes of pollution9, and10 employed the WRF/CMAQ coupled model to explore the spatiotemporal distribution characteristics of air pollution. Additionally11 and12, developed regional transport models to assess the contributions of various pollutants to PM2.5, particularly in the Beijing- Tianjin-Hebei (BTH) region13 and14 analyzed the sources and dynamic changes of pollutants to reveal the relative contributions of different pollution sources. Although the IoT GPRS sensor array and the WRF/CMAQ coupled model effectively map the spatial distribution of pollution, their reliance on static sensor networks and computational intensity limits real-time dynamic prediction capabilities. The STIRPAT and regional transport models elucidate socioeconomic drivers and pollutant transport but fail to capture the nonlinear temporal dependencies of concentration fluctuations. Consequently, accurately predicting PM2.5 concentrations and dynamically monitoring real-time changes in pollution levels to provide a scientific basis for government pollution control policies has become an urgent issue to address.

In recent years, numerous models have been extensively applied to prediction tasks, including statistical models, machine learning models, and deep learning models. Among these, the application of single classical models is particularly widespread. For example15, used the ARIMA model to forecast the concentration of submicron particles16 applied Support Vector Machines (SVM) to predict PM2.5 concentrations and the levels of heavy metals in PM2.5. 16 employed Random Forest (RF) to predict heavy metals in soil, while17 and18 used Artificial Neural Networks (ANN) and Chaotic Artificial Neural Networks (CANN) for PM2.5 prediction and analysis19 and10 utilized Recurrent Neural Networks (RNN) for indoor PM2.5 concentration forecasting. Similarly20,21,22, applied Backpropagation Neural Networks (BPNN) for regression-based PM2.5 forecasting. Moreover23, incorporated optimization algorithms into single models to enhance their performance. These single models feature straightforward and simple structures, with relatively low computational costs. However, they typically exhibit inherent limitations. For instance, RNNs often suffer from vanishing or exploding gradient problems when processing long time-series data. Although LSTM models outperform Convolutional Neural Networks (CNNs) and Gated Recurrent Units (GRUs) in time-series processing24, their high sensitivity to hyperparameters makes optimization particularly challenging. Similarly, statistical models such as ARIMA struggle to handle multidimensional and complex datasets25.

To address these challenges, we propose a hybrid deep learning model with three key innovations, designed to integrate complementary advantages through model fusion and achieve more accurate air pollution prediction. First, the model combines the gated temporal memory of LSTM with the self-attention mechanism of Transformer, enabling it to simultaneously capture long-term dependencies in time-series data and global dependencies within sequences. Second, the model incorporates a Particle Swarm Optimization (PSO) algorithm to automatically adjust parameters, overcoming the manual calibration bias inherent in traditional LSTM implementations. Third, the model resolves the challenges of multi-scale temporal dependencies, multi-variable coupling, and parameter tuning in air pollution prediction through synergistic optimization of algorithms and models, as well as joint modeling of spatiotemporal features. By integrating these three components, the proposed model captures both the long-term dependencies and global characteristics of PM2.5 concentration variations, significantly improving prediction accuracy.

The superiority of the new model was validated through empirical studies across different cities and periods. Comparative experiments with LSTM-solely (L-solely) and PSO-LSTM models demonstrated that the proposed hybrid model outperforms existing methods in terms of prediction accuracy, performance, and stability. This research not only provides an innovative solution for PM2.5 concentration forecasting but also offers theoretical support and practical insights for modeling multi-dimensional dynamic spatiotemporal data. The findings serve as an important reference for the scientific management of air pollution.

The remainder of this study is organized as follows. Section Construction of PSO-transformer-LSTM network reviews the fundamental concepts of Transformer and LSTM and introduces the network architecture of the proposed PSO-Transformer-LSTM model. Section Data describes the data selection and preprocessing procedures. Section Experiment and analysis outlines the performance evaluation metrics used in the experiments. Section 5 presents the technical framework of the experiments and validates the accuracy and stability of the proposed model under varying conditions, including different cities and time spans, using multiple evaluation metrics. Finally, Section Conclusion concludes the work.

Construction of PSO-transformer-LSTM network

The proposed PSO-Transformer-LSTM model is a hybrid architecture that integrates the advantages of the transformer model, the LSTM network and the particle swarm optimization (PSO) algorithm. This section describes the main components of the model and their interconnections. First, the positional coding layer: to address the transformer’s lack of intrinsic order awareness, positional coding is introduced to embed order information into the input data. Second, the self-attention layer: the self-attention mechanism captures global dependencies in the input sequences, enabling the model to effectively handle long-range interactions. Additionally, the LSTM network: the LSTM gating mechanism complements the transformer by capturing long-run temporal dependencies in the data. Finally, the PSO optimization: the PSO algorithm optimizes the key hyperparameters of the hybrid model, thus improving its overall performance.

By combining these components, the PSO-Transformer-LSTM model effectively leverages the global feature extraction capabilities of Transformer, the temporal dependency modeling of LSTM, and the parameter optimization of PSO to achieve accurate and robust PM2.5 predictions.

Position encoding layer

The transformer model is a deep learning architecture that has achieved significant advancements in fields such as natural language processing (NLP) in recent years. Unlike traditional Recurrent Neural Networks (RNNs) and LSTM networks, the Transformer does not rely on recursion or convolution to process input data, resulting in a substantial improvement in parallel processing capabilities. However, due to the absence of sequence structural information, the Transformer cannot inherently perceive the positional relationships among elements in the input sequence. To address this, the Positional Encoding mechanism is introduced. Positional Encoding generates specific vectors for each position, which are added to the input embeddings, enabling the model to capture the sequential order of elements. Typically, positional encoding uses a set of fixed sine and cosine functions to generate the encoding by separating data into even and odd indices, ensuring the model can distinguish elements at different positions. The calculation is defined by Eqs. (1) and (2), where PE represents the positional encoding, pos denotes the position in the sequence, is the dimension index of the positional encoding, and d is the embedding dimension size.

$$PE_{{\left( {pos,2i} \right)}} = sin\left( {\frac{pos}{{10000^{\frac{2i}{d}} }}} \right)$$
(1)
$$PE_{{\left( {pos,2i + 1} \right)}} = \cos \left( {\frac{pos}{{10000^{\frac{2i}{d}} }}} \right)$$
(2)

Before entering the Transformer encoder layer, the positional encoding must be combined with the input information to ensure that the processed input retains both the original information and its positional context within the sequence. Let the input information be E, the positional encoding be PE, and the resulting input be E0. The calculation is expressed as Eq. (3).

$$E_{0} = E + PE$$
(3)

where E represents the input embedding matrix, and PE is the positional encoding matrix corresponding to each position. This additive operation preserves the positional characteristics of each input element without altering the dimensional structure of the embeddings. This enables the subsequent Transformer encoding layers to effectively incorporate sequence order information. The structural diagram illustrating this process is shown in Fig. 1.

Fig. 1
figure 1

Structure diagram of position encoding layer.

Full size image

Self-attention layer

Self-Attention, as a core component inside the Transformer, can capture the dependencies between elements at different locations in the input sequence. After the input data is fused with the positional encoding, the Self-Attention mechanism can process the data while paying attention to the global information of all elements in the sequence, which undoubtedly greatly improves the efficiency of parallel computation and solves the problem of long-distance dependency.

The self-attention mechanism works in the sense that the input is a sequence of vectors, and the output is a weighted sum of each element in that sequence over all other elements. Each element determines its contribution to the weighted sum based on its relevance to the other elements. Specifically, the self-attention mechanism generates three new vectors by performing three linear transformations on the input elements: the query vector (Q), the key vector (K), and the value vector (V). Where Q denotes the information that needs to be queried from the sequence, K denotes the keys that can be compared with the query information, and V denotes the values that correspond to K. These vectors are transformed by the output of the previous layer. For each element in the sequence, its correlation with other elements is computed, and the formula is as follows. Where QKT denotes the dot product of the query vector and the key vector, and the result of the dot product denotes their similarity. \(\sqrt{{d}_{k}}\) is the scaling factor to avoid too large a value of the dot product affecting the stability of the gradient, and dk is the dimension of K. The SoftMax function normalizes the result of the dot product, and what is obtained is the attentional weights, which are used to weigh and sum up the corresponding V.

$$Attention(Q,K,V) = softmax\left( {\frac{{QK^{T} }}{{\sqrt {d_{k} } }}} \right)V$$
(4)

A weighted summation of the values of V for each element is performed using the attention weights obtained from the above computation. The final output of each query vector is a weighted combination of all the values of V with weights determined by their similarity to the K of the other elements.

In order for the model to capture information about different relationships at multiple levels at different locations of different features in the sequence. Multi-head Attention Mechanism is used in the Transformer model. The multi-head attention mechanism is composed of multiple heads with self-attention, and the core idea is to compute different self-attention results for Q, K, and V through multiple heads, then stitch these results together, and finally output them through a linear transformation. This mechanism enables the model to focus on different features in the sequence in different subspaces. Its calculation formula is as follows.

$$MultiHead(Q,K,V) = Concat(head,...,head_{h} )W^{O}$$
(5)

The formula for each of these heads is as follows. Where WO is the linear transformation matrix passed after splicing, QWiQ, KWiK and VWiV are the weight matrices used to linearly map the input Query, Key and Value to different subspaces.

$$head_{i} = Attention(QW_{i}^{Q} ,KW_{i}^{K} ,VW_{i}^{V} )$$
(6)

LSTM

In a general feedforward neural network (FNN), neuron A recursively calls itself and passes the information from moment t−1 to moment t, the RNN structure is shown in Fig. 2. Usually, recurrent neural networks work well, especially when facing problems that require a short period to memorize, however, when the time series becomes longer and more information needs to be retained, the ordinary recurrent neural networks then suffer from the gradient vanishing problem and the gradient explosion problem.

Fig. 2
figure 2

Recurrent neural network architecture.

Full size image

LSTM is a specialized type of Recurrent Neural Network (RNN) designed to process sequential data. It represents an improved version of traditional RNNs, specifically addressing the issues of gradient vanishing and exploding gradients when handling long-term dependencies. In the chain-like structure of a standard RNN, each module contains only a single Tanh layer. In contrast, the LSTM’s chain-like structure includes four distinct layers within each module, namely the input gate, forget gate, output gate and memory cell. These gated structures work together to enable LSTM networks to effectively capture and retain long-term dependency information, thereby overcoming the gradient vanishing issue associated with traditional RNNs when learning long sequences. The internal structure of the LSTM is illustrated in Fig. 3.

Fig. 3
figure 3

Structure of LSTM.

Full size image

There are the Sigmoid function and Tanh function in the LSTM network structure. The output of the Sigmoid function is a value between 0 and 1, which is used to control how much information passes through. The Sigmoid function is used in the Forget gate to decide which past information needs to be retained and which needs to be forgotten. If the output is close to 1, more information is retained; if it is close to 0, most of the information is forgotten. Similarly in Memory Gate and Output Gate. The Tanh function normalizes the input data and output values between − 1 and 1, which are used to scale the information. In LSTM, the Tanh function is usually used to generate new memory content and output content, so that the memory cell state can contain changes in both positive and negative directions. Thus, the information is better forgotten or retained. Its calculation formula is as follows. Where S(x) is the output value of the Sigmoid function, denoting the result after a nonlinear transformation, ranging from (0, 1). x is the input information. Tanh (x) is the output value of the Tanh function, ranging from − 1 to 1. Indicates the result of the input after Tanh's nonlinear transformation.

$$S(x) = 1/(1 + e^{( - x)} )$$
(7)
$$Tanh(x) = (e^{x} - e^{( - x)} )/(e^{x} + e^{( - x)} )$$
(8)

The forget gate controls which information needs to be forgotten or discarded from the memory cell and determines the state update of the memory cell. The forget gate outputs a value between 0 and 1 through the Sigmoid function, with 0 indicating complete forgetting and 1 indicating complete retention. The formula is as follows. Where ft is the output of the forget gate, Wf is the weight matrix, bf is the bias, ht–1 is the bias, and xt is the input of the current time step.

$$f_{t} = \sigma \left( {W_{f} * \left[ {h_{t - 1} ,x_{t} } \right] + b_{f} } \right)$$
(9)

The input gate determines how much information from the inputs of the current time step needs to be added to the memory cell. The role of the input gate is to update the state of the memory cell by combining the new input with the existing state. It uses a gating mechanism to control the proportion of new information to be retained before updating the memory cell state. The formula is as follows. Where it is the output of the input gate that controls how much of the new information is to be updated in the memory cell. \(\widetilde{{C}_{t}}\) is the candidate vector created by Tanh which is added to update the memory state.

$$i_{t} = \sigma \left( {W_{i} * \left[ {h_{t - 1} ,x_{t} } \right] + b_{i} } \right)$$
(10)
$$\widetilde{{C_{t} }} = {\text{Tan}}h\left( {W_{C} *\left[ {h_{t - 1} ,x_{t} } \right] + b_{C} } \right)$$
(11)

The key to LSTM is the hidden state of neurons. The hidden state of a neuron is simply understood as the “memory” of the recurrent neural network for the input data. This memory Ct covers all the input information of the neural network until t + 1 moment. The formula is as follows. Where Ct is the memory information at time t. Ct−1 is the memory information at time t−1. From this formula, it can be seen that the current memory information is composed of the previous memory information together with the current new information.

$$C_{t} = f_{t} * \left( {C_{t - 1} + i_{t} * \widetilde{{C_{t} }}} \right)$$
(12)

The output gate determines how much information from the current state of the memory cell needs to be output to the next time step. The output of the output gate becomes the hidden state of the current time step and participates in the computation of the next time step. The formula is as follows. Where ot is the result of the output gate, which decides which information needs to be output. ht is the hidden state of the current time step.

$$o_{t} = \sigma \left( {W_{o} *\left[ {h_{t - 1} ,x_{t} } \right] + b_{o} } \right)$$
(13)
$$h_{t} = o_{t} *Tanh\left( {C_{t} } \right)$$
(14)

For inputting long data series, not all information is equally important. Sometimes we need to remember the important information or key information. So the retention of valid information and the screening of invalid information are especially important. LSTM optimizes the capture of long-time dependencies by precisely controlling the weights of different information. Through the synergistic effect of forgetting gate, input gate, and output gate, LSTM not only effectively solves the shortcomings of traditional RNN in dealing with long sequences, but also effectively rejects and retains information. Thus, it demonstrates unique advantages in long-dependent information tasks that require memorization and updating.

Overall network structure of PSO-transformer-LSTM

In this study, we combined the Transformer model with the LSTM model and incorporated the particle swarm optimization (PSO) algorithm to optimize the parameters of it. The PSO optimization algorithm is chosen because it does not have too many parameters to be tuned and it can also be quickly combined with other models. PSO as a branch of evolutionary computation is an on-the-fly search algorithm that simulates biological activities in nature as well as group intelligence. The algorithm obtains optimization results by generating particles of a certain size as effective solutions to the search space of the problem and then performing an iterative search. Many scholars utilize the grid search method to adjust the parameters26, which greatly reduces the efficiency of experimental runs. By invoking the PSO optimization algorithm to help the model find the optimal parameters can effectively avoid the tedious process of tuning parameters. And it can effectively improve the prediction efficiency and accuracy of the model.

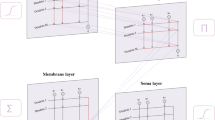
The new model incorporates location information into the input features through a location embedding layer to compensate for the lack of sensitivity of the Transformer model to location information. The self-attention mechanism is utilized to capture the dependencies between distant elements in the sequence to improve the model’s ability to capture global features. The long-term dependencies in the sequence data can be captured by the gating mechanism of LSTM. By combining them, we created the PSO-transformer-LSTM model, whose internal structure of the unit is shown in Fig. 4.

Fig. 4
figure 4

Internal structure of the PSO-transformer-LSTM model.

Full size image

In the structure of the model, the position-coding layer encodes the position information into the input information and enters the summation layer with the input information. This allows the input data to be fused with the location information. The fused information is passed to two multi-attention layers. The first self-attention layer carries a causal mask. This mask restricts the model to see only the current time step and the time step before it. Thus, the temporal sequence is ensured. It is crucial for time series forecasting. Because such tasks usually require the model to make predictions based on historical information only. This layer is mainly used to extract the time-dependent features of the input series and also ensures that the causality is reasonable.

The second self-attention layer does not carry a causal mask, so it is free to compute attention weights over the entire range of the sequence. This means that each position can interact with all other positions. Its role in this model is to further extract global features and enhance the ability to model long-distance dependencies between sequences. Through this layer, the model can better capture the global correlations in the input sequences. Overall, by using the two self-attentive layers, models can capture both local temporal sequence information and extract global features, thus providing richer feature representations for subsequent LSTM layers. Combining the additive layer of position encoding and the subsequent LSTM layer, the model can better handle complex time series data and improve the accuracy of prediction.

After passing through the self-attention layer, the feedforward layer starts feature mapping the output of the self-attention layer. It maps the features from the output of the self-attention layer to a higher dimensional space. The rectified linear unit (ReLU) introduces nonlinearity to enhance the model’s fitting capability. Then fully connected layer further maps the output of the feedforward layer to the desired input dimensions of the LSTM layer. Ensuring that features are more fully extracted before being passed to the LSTM.

Once in the LSTM layer, the LSTM gating mechanism captures the timing dependency information of the input features. The PSO will optimize the model’s Batch size, initial learn rate, L2Regularization, and the number of hidden units to achieve the optimal parameter combinations in this process. In this way, the learning ability of the model on time series features is improved. The linear rectification layer is immediately followed by the introduction of nonlinear features again. The model can learn more complex mapping relationships. We introduce a deactivation layer (Dropout) before the output in order to prevent the model from overfitting. By randomly dropping some neurons during the training process, the generalization ability of the model is improved. Finally, the model completes the final output at the end of a series of mappings.

Through the above steps of the information process, the information completes the computation in one unit. During this process, the memory information Ct and output information ht connecting each unit are also transferred between each unit.

Data

Data description

Our previous research has showed that Wuhan, as one of the centers of the spatial network of urban agglomerations in the Yangtze River Economic Belt, plays an important role in PM2.5 transmission in the region27. Meanwhile, Hu’s study confirmed that Nanchang, as the core city of Jiangxi Province, is the main medium city for haze propagation in the province28. In order to verify the model performance from multiple perspectives, this study chooses Nanchang and Wuhan as the study area and tests the model through different time spans. In this work, we use PM2.5 monitoring data from January 1, 2018, 00:00 to December 31, 2022, 23:59. The monitoring indicators include PM2.5, CO, NO2, O3, PM10, SO2, maximum and minimum temperature of the day. The data were processed as follows: first, calculating the hour-by-hour monitoring data as daily averages; second, averaging the daily averages at different stations to obtain the day-by-day averages for Nanchang and Wuhan. The input features of the model include CO, NO2, O3, PM10, SO2, maximum and minimum air temperature of the day, and PM2.5 is used as the prediction target. It is worth noting that air quality monitoring data may have missing values due to sensor failures or network outages. And data containing null values may lead to unreliable output. Therefore, before prediction, this study used linear interpolation to fill in the missing data to ensure data integrity and accuracy of prediction results. Measurement data for each site in each city and the geographic location of each site were obtained from the Institute of Geographic Sciences and Resources, Chinese Academy of Sciences (http://envi.Ckcest.cn/environment/).

Analysis of characteristics

Correlation analysis is a statistical method used to assess the correlation between two or more variables. The correlation analysis identifies whether there is a significant correlation between the independent variables and the dependent variable. In this way, irrelevant or weakly correlated variables can be eliminated, and model performance can be improved. Pearson correlation analysis is one of the methods. In this work, we use Pearson correlation analysis to measure the linear correlation between variables. The Pearson correlation coefficient ranges from − 1 to 1, where positive values indicate positive correlation and negative values indicate negative correlation. The closer the absolute value of the coefficient is to 1, the stronger the correlation is. In order to visualize the relationship between the features, this study visualizes the correlation between the variables through heat maps.

By analyzing (Fig. 5) of the correlation analysis chart, it can be found that the seven features in the data are significantly correlated with PM2.5 in both Nanchang and Wuhan. That is, the P-value between them is less than or equal to 0.05. The correlation coefficients between PM10 and PM2.5 in Nanchang and Wuhan are even as high as 0.84 and 0.81. Besides the P-value of O3 and PM2.5 in Nanchang is within the range of 0.0001 to 0.001. All the remaining features had P-values less than 0.0001 with PM2.5. Therefore, these seven features were retained as feature inputs to the model.

Fig. 5
figure 5

The figure of correlation analysis.

Full size image

Data standardization

The original dataset contains characterization data for different aspects such as air quality, and temperature. And the unit of measure is different from feature data to feature data for all features. If the feature values in the dataset have large magnitude differences and are not normalized, the features with larger magnitude will dominate the decision-making process of the model, weakening the influence of the smaller features. Normalization ensures that each feature is in the same range, making the model treat all features more fairly. We use Min–Max normalization to scale the data between 0 and 1. The formula for this is as follows. Where X0 is the data obtained after normalization, X is the data before normalization, and Xmin and Xmax are the minimum and maximum values of the data before normalization.

$$X_{0} = \frac{{X - X_{{{\text{Min}}}} }}{{X_{{{\text{Max}}}} - X_{{{\text{Min}}}} }}$$
(15)

Performance evaluation

In order to comprehensively assess the performance of the model, this study selected five commonly used evaluation metrics. Including the coefficient of determination (R2), mean absolute error (MAE), mean bias error (MBE), root mean square error (RMSE), and mean absolute percentage error (MAPE). Where yi is the true value, \(\widehat{{y_{i} }}\) is the predicted value, \(\overline{{y_{i} }}\) is the average of the true values. n denotes the number of test values.

R2 indicates how well the model explains the variation in the data. Its value ranges from 0 to 1. The closer R2 is to 1, the better the model fits the actual data, and on the contrary, the closer it is to 0, the worse the model is. The formula is as follows.

$${\text{R}}^{2} = 1 - \left( {\sum\limits_{1}^{n} {\left( {\widehat{{y_{i} }} - y_{i} } \right)^{2} /} \sum\limits_{1}^{n} {\left( {\overline{{y_{i} }} - y_{i} } \right)^{2} } } \right)$$
(16)

MAE is the average of the absolute values of the errors between the predicted and true values. The smaller the MAE value, the lower the prediction error of the model. MAE provides a more balanced view of model fit for evaluating predictive models. The formula is as follows.

$${\text{MAE}} = \frac{1}{n}\sum\limits_{i = 1}^{n} {\left| {\widehat{{y_{i} }} - y_{i} } \right|}$$
(17)

MBE indicates the average deviation of the forecast value relative to the true value, reflecting the overall directional bias of the forecast, with positive values indicating overestimation and negative values indicating underestimation. The formula is as follows.

$${\text{MBE}} = \frac{1}{n}\sum\limits_{i = 1}^{n} {\left( {\widehat{{y_{i} }} - y_{i} } \right)}$$
(18)

RMSE is the mean square of the squared error between the predicted value and the true value, which is used to measure the standard deviation of the prediction error. RMSE is more sensitive to outliers, the smaller the value the better the model performance. The formula is as follows.

$${\text{RMSE}} = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^{n} {\left( {\widehat{{y_{i} }} - y_{i} } \right)^{2} } }$$
(19)

MAPE is the percentage average of the absolute error between the predicted value and the actual value. MAPE indicates the percentage of the prediction error to the real value, the smaller the value the better. The formula is as follows.

$${\text{MAPE}} = \frac{1}{n}\sum\limits_{i = 1}^{n} {\left| {\frac{{\widehat{{y_{i} }} - y_{i} }}{{y_{i} }}} \right| * 100\% }$$
(20)

In the PSO optimization process, we use mean square error (MSE) as a fitness function. MSE will increase significantly because of the square of the error. So, there is a higher penalty for larger errors. It makes the model more focused on reducing larger prediction errors during training, which improves the overall accuracy of the model. In addition to these evaluation metrics, we also use linear fit graphs, scatter plots, and multi-factor histograms to demonstrate the performance of the model.

Experiment and analysis

We build the technical route before experimenting. It is divided into four parts according to the functions: data preprocessing, model building, PSO parameter optimization, and model validation. The technology roadmap is shown in Fig. 6.

Fig. 6
figure 6

Model technology roadmap.

Full size image

To facilitate the narrative of the experimental results, we refer to the L-solely model, PSO-LSTM model, and PSO-Transformer-LSTM model as L-solely, PL, and PTL models, respectively. We conduct tests in different periods and different lengths in Nanchang and Wuhan to verify the accuracy and generalization of the models. There are three lengths of the dataset, which are four season (we take spring as an example in this work), a year and 4 years. We divide the experiments for each city into three parts according to the length of the dataset to show the performance of different models. The data for the cities are preprocessed. The data are imported into the model and the model is tested as in Table 1.

Table 1 Table of model prediction results.
Full size table

The data in the table shows that the PTL model performs well in the three-time intervals of the two cities, especially in the “one quarter” period, where the PTL model shows the best performance with R2 of 0.98745 and 0.95655, which indicates that its predicted values are highly correlated with the actual values. In addition, the PTL model maintains lower MAE, MBE, RMSE, and MAPE values of 0.83363 1.2954, 1.0176, and 1.502, respectively, which further indicates that its prediction error is low, and it has strong prediction ability.

However, the prediction accuracy of the model decreased as the time of the test data increased. This phenomenon is consistent with the results of machine learning-based water quality prediction studies at multiple time scales29,30. That is, the model’s prediction difficulty increases, and the accuracy decreases with the extension of the period. Nevertheless, the PTL model still performs well in all time intervals, with R2 values remaining above 0.8 and low prediction errors. It shows that it still has superior adaptability and stability when dealing with the prediction task in different time intervals.

The PTL model also improves in performance compared to the L-solely and PL models. For the “one quarter” time horizon, the R2 of the PTL model improves by 7.3% and 12.6% compared to the L-solely model, and by 2.3% and 9.8% compared to the PL model. In the tests for the “2022” time horizon, the R2 of the PTL model was 11% and 9.7% higher than the L-solely model and 10.2% and 5% higher than the PL model, respectively. In the tests for the “2018–2021” time horizon, the R2 of the PTL model is 7.1% and 13.3% higher than that of the L-solely model and 3.3% and 7.4% higher than that of the PL model, respectively. In addition, the PTL model outperforms the L-solely and PL models in the error metrics of MAE, MBE, RMSE, and MAPE. Figures 7, 8, 9, 10, 11, 12 shows the test results of three models in three time periods in Nanchang and Wuhan.

Fig. 7
figure 7

The seasonal test of three model in Nanchang.

Full size image
Fig. 8
figure 8

Three model test in Nanchang in 2022.

Full size image
Fig. 9
figure 9

Three model test (2018–2021) in Nanchang.

Full size image
Fig. 10
figure 10

The seasonal test of three model in Wuhan.

Full size image
Fig. 11
figure 11

Three model test in Wuhan in 2022.

Full size image
Fig. 12
figure 12

Three model test (2018–2021) in Wuhan.

Full size image

The Figs. 7, 8, 9, 10, 11, 12 allow visual comparison of the models’ prediction results under the same city and time conditions. The comparative analysis reveals that the PTL model fits significantly better than the L-solely and PL models. The scatter plots reveal the relationship between the predicted values and the true values, and the superiority of the PTL model in the fitting effect can be seen by observing the trend, outliers, clusters, and the proximity of each point to the fitted straight line. It shows that the PTL model outperforms the independent model before optimization under different cities and periods.

To further validate the stability of the model, we averaged the first ten times of the test results. The following Fig. 13 shows the average errors of the L-solely, PL, and PTL models over three time spans in two cities. The vertical lines in the bar graph indicate the upper and lower deviation ranges of the test values, and the Y-axis indicates the average error of each model.

Fig. 13
figure 13

Average error statistics chart.

Full size image

What’s more, it can be found that the minimum average errors of the L-solely and PL models are 1.4573, 7.9146, and 5.0543 for the three time periods in Nanchang, for the PTL model, the average errors are 0.9023, 6.27927 and 4.7786, respectively. For the Wuhan data, the minimum mean errors of the L-solely and PL models for the three time periods were 2.32998, 6.8713 and 5.5113, respectively. The mean errors of the PTL model were 1.50961, 6.1192 and 5.2637. Overall, the PTL model had smaller prediction errors for most of the test conditions, suggesting that it has a higher degree of accuracy.

In addition, by observing the up-and-down fluctuations of the errors, it is found that the PTL model has the smallest up-and-down fluctuations, and the stability of the PTL model is significantly better than that of the L-solely and PL models. This indicates that the PTL model not only performs superior in accuracy but also shows stronger stability in the prediction of different periods and cities.

Conclusion

For environmental protection and sustainable development, accurate prediction of air pollution is essential. In this paper, a composite model based on deep learning is presented, aiming to accurately predict air pollution concentration. It is based on the L-solely model combined with the Transformer model, and the PSO optimization algorithm is used to find the optimal hyperparameters in the model.

To verify the prediction ability of the model, this work selects two cities, Nanchang and Wuhan, and chooses three different periods of data for experiments. The experimental results show that the prediction accuracy of the PTL model is better than that of the L-solely and PL models before optimization under different city and period conditions, showing a better prediction effect. There are three main reasons for this improvement. First, the model is improved based on L-solely, which has been proven to be powerful in many prediction tasks. Its unique gating mechanism effectively filters out valuable information and removes irrelevant or redundant parts, ensuring the capture of long-term dependencies. Second, introducing the PSO optimization algorithm significantly reduces the time for hyper-parameter tuning and can find more appropriate model parameters, thus improving the model performance. Finally, the introduction of the Transformer model enables the model to efficiently process positional information and enhance the interrelationships between the information through positional encoding. Its self-attention mechanism enables the model to capture the dependencies between individual pieces of information as well as with global information, thus improving the prediction.

The experimental results show that the PTL model provides accurate and stable prediction results for all three time periods in the cities of Nanchang and Wuhan. Compared with the L-solely and PL models, the PTL model performs better in the performance metrics of R2, MAE, MBE, RMSE, and MAPE. The results of this study provide an effective method for accurate prediction of PM2.5 concentration in the absence of observational data. It also provides data support and a theoretical basis for the government to formulate scientific pollution control policies.

Although the focus of this study is on PM2.5 prediction, the proposed PTL model demonstrates significant potential for broader applications in time-series forecasting tasks. The hybrid architecture integrates global dependency modeling (via Transformer), temporal dynamic learning (via LSTM), and parameter optimization (via PSO), making it adaptable to other environmental and meteorological scenarios. For example:

  1. 1.

    Air Quality Index (AQI) Prediction: By incorporating additional pollutants (e.g., NO2, SO2, O3, PM10) and meteorological variables, the model can predict comprehensive AQI values, thereby supporting real-time air quality management31,32.

  2. 2.

    Meteorological forecasting: The model’s ability to capture spatiotemporal correlations makes it suitable for predicting temperature, humidity, or extreme weather events (e.g., typhoon trajectories) when trained on multi-source climate data33.

  3. 3.

    Urban traffic flow prediction: Integrating traffic sensor data (e.g., vehicle speed, congestion rates) enables the model to predict short-term traffic patterns, providing support for smart city planning34.

  4. 4.

    Energy consumption analysis: The model can forecast electricity demand or renewable energy generation (e.g., solar/wind power) by learning from historical consumption data and weather conditions35,36.

  5. 5.

    Battery performance prediction: The model can predict the performance of Proton Exchange Membrane Fuel Cells (PEMFCs) using battery data (e.g., cycle count, voltage), thereby extending their lifespan and enhancing their commercial value37,38,39.

Future research will explore these directions to validate the model’s versatility. Furthermore, During the experiments, we observed that the L-solely model alone was capable of learning approximately 83 parameters. In contrast, the proposed model exhibited a significant increase in the number of trainable parameters, exceeding 100,000 as the number of attention heads increased. This rise in trainable parameters led to a corresponding increase in training time. Compared to the L-solely and PL models, the PTL model demonstrated higher complexity and a greater number of learnable parameters, necessitating more time for training. However, similar to the PL model, the majority of the PTL model’s runtime was dominated by the PSO process, resulting in only a marginal increase in training time compared to the other two models. Importantly, the PTL model was able to uncover more intricate relationships within the data, leading to a significant improvement in prediction accuracy.