Introduction

Nowadays, various events in track and field have been greatly developed internationally, and in the process, the impact of running speed on athletes has become increasingly significant, which has attracted widespread attention from coaches and researchers. Accurate and excellent footwork can greatly improve the training effect of athletes, as well as the professional level of athletes. Up to now, the research on the footwork of track and field athletes has mostly focused on a specific competitive event, such as the step and jump movements of the long jump, the start of the 100 m running, and so on. This article summarizes the footwork of track and field athletes through the analysis of examples of the 100 m dash, providing a certain theoretical basis and scientific guidance for the training and competition of track and field athletes.

In track and field competitions, track and field performance is the focus of people’s attention. Currently, there are many studies that affect track and field performance1,2. For example, Close G L3 believed that injuries are an important factor affecting athletes’ performance, with hamstring injuries being the most common injury so far (approximately 17%), and male athletes are more frequent than female athletes. There are subtle differences between different types of health problems. Athletes who perceive more social pressure and competitive injuries, and athletes with higher performance levels, are more likely to become a group of athletes who dislike rest or despise pain. Among them, more researchers suggest that there is a greater correlation between footwork and track and field performance. Wang Jianming and others used data preprocessing, wavelet packet transform, and waveform and parameter estimation methods to analyze and obtain sprint gait waveform estimates within the observation interval, and then estimated sprint parameters such as average speed, number of steps, step length, and step frequency within the interval4. Wang Junqing explored the impact of step frequency control training on the impact of running landings, kinematics and dynamics of the lower limbs, hips, knees, and ankles, with a view to reducing running impact and improving running performance by increasing step frequency5. These studies have to some extent promoted the development of track and field sports, but the methods they used were too traditional and did not well integrate with new technologies.

With the development of image processing technology, its integration with motion recognition has become increasingly close6,7. There are also many studies on using image processing to track and standardize actions. For instance, Zhou Qinqin8 studied multi-person tracking and motion reasoning based on deep alignment networks. To make the deep features of alignment networks have better expressiveness and more consistent trajectory, he designed a coarse-to-fine pattern for constructing trackers with spatial, motion, and appearance information. His experiments have shown that the proposed tracker is effective and robust. Keuper Margret9 explored joint clustering for motion segmentation and multi target tracking. He proposed the idea of combining bottom up motion segmentation through point trajectory grouping with advanced multi target tracking through boundary box clustering to improve the efficiency of motion segmentation and multi target tracking, and confirmed its effectiveness. Liu Xingtong10 developed a golf swing motion analyzer system using image recognition technology. This used the inter frame difference method to compare the change trend of the two frames before and after the swing to determine whether the designated part of the body moved during the swing process and gave an alarm. The analyzer system can help golfers correct their swing movements and make golf teaching more intuitive. Wu Kai11 proposed a palm vein recognition network PVCodeNet, described key point positioning, ROI extraction and image enhancement, and conducted detailed experiments on the feature vector dimension and AAM-loss parameter setting. With the assistance of intelligent algorithms, footwork recognition and trajectory tracking technologies have achieved further development, but most studies have only explored the improvement and improvement of trajectory tracking technology from a theoretical level, and the improvement of trajectory tracking accuracy has not been well verified in the actual development process.

To better improve the efficiency of track and field athletes’ footwork recognition and trajectory tracking, this article uses image processing technology with SVM algorithm as the core to improve the efficiency of track and field athletes’ footwork recognition and trajectory tracking. An experiment was conducted to identify and track the footwork of school track and field team athletes before and after their footwork was standardized. The results showed that the deviation of real-time trajectory tracking movement in this paper was very small, and the athletes’ performance had been improved. Compared to conventional research, the innovation of this project is the organic integration of support vector machines and image processing technology, which has important theoretical and practical significance in promoting post competition data analysis and improving athletes’ training effectiveness.

Image denoising and feature extraction classification

The traditional way of training is for a coach to stand by, observe, record, and analyze an athlete’s training or competition. Then the coach’s years of teaching and training experience is used to guide athletes and develop corresponding training programs for them. However, this method of analysis and training has the following disadvantages. First of all, the existing team of coaches is very small, making it difficult to keep up with the number of competitors, thereby reducing the training effectiveness of athletes. Secondly, the traditional method of foot movement based on eye observation cannot accurately obtain the acceleration, angular velocity, and other data in foot movement, making it difficult to grasp the deep information that affects foot movement, and cannot conduct detailed analysis of these data. Therefore, in track and field teaching, traditional teaching methods can no longer meet the needs of modern track and field teaching, and there is an urgent need for a more intelligent, comprehensive, and convenient teaching method.

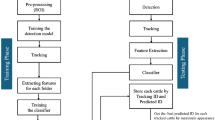
With the continuous development of computer technology, image processing technology can collect and classify key factors such as the movements and footwork of track and field athletes, which can effectively standardize the movements of track and field athletes and improve their performance. This makes modern track and field training more targeted and purposeful, making training more scientific and quantitative and thereby improving the overall level of track and field. The general framework of track and field image processing in this article is shown in Fig. 1.

Fig. 1
figure 1

Framework for image processing.

Full size image

Image denoising

As technologies such as the Internet of Things and computer image processing continue to advance, data analysis and training of athletics competitions have gradually moved from relying solely on manual records and coaches’ experience to an intelligent and smart data analysis and training system for athletics. The researchers use image processing technology to combine a variety of sports scenes to achieve recognition and tracking of athletes’ technical movements.

During the process of image acquisition, due to the interference of various factors, it can bring noise to the image, manifested as different forms of interference points or stripes. Therefore, ensuring that the image is minimally contaminated has become an important content in the field of digital image processing. When noise occurs in an image, its quality may significantly decrease, and at the same time, information may also be seriously affected. Therefore, before performing edge detection, segmentation, and information extraction on an image, it is also necessary to filter the image to exclude the impact of noise on the image12.

Median filtering13 is relatively effective for impulse noise, but its directionality is poor. Mean filtering can smooth an image, but it cannot remove noise and can only weaken it. Gaussian filter is a smoothing filter based on frequency domain, which is a local filter. However, using traditional Gaussian filter alone to eliminate image noise still has shortcomings. Taking into account the characteristics of these filters, this paper selects a reduced median filter and a mean filter algorithm14 to denoise twice before and after. Mean filtering achieves the effect of smoothing the image by calculating the average value of the neighboring pixel values around a pixel to replace the pixel value. It is suitable for removing some uniformly distributed noise, but may cause loss of image details, especially the edges may become blurred. In contrast, median filtering is to sort the neighboring pixels and select the median as the new pixel value, which can effectively remove salt and pepper noise (i.e., extreme noise in the image) while better retaining the edge and detail information of the image. Median filtering can avoid excessive blurring of the image while denoising, so it is usually more effective than mean filtering when processing images with sharp noise. Taking the 100 m dash as an example, this article collects videos of some sprinters’ training and competition. 3% salt-and-pepper noise is added to the original image, and after the initial denoising through 3*3 module median filtering, the white and black spots of the interfering image can be removed. However, compared to the original image, the image is still a bit blurry, mainly due to the fact that during filtering, regardless of whether the pixel is contaminated or not, it is replaced by a median value, resulting in some areas of the image still blurry. The effect would be better if it could be further sharpened. It is assumed that the noise in the input image is uniform, but when the sampling rate is insufficient, the resulting image may contain highly uneven noise, whose type and size depend on the scene geometry, object material, light transmission, and lens effect. This paper uses the method of mean filtering to remove noise. The images before and after median filtering and mean filtering are shown in Fig. 2.

Fig. 2
figure 2

Results after image denoising.

Full size image

As can be seen, comparing pixel points with median values, if they are greater than the threshold value, it is treated as noise and should be replaced. If it is less than the threshold value, it indicates that the pixel point is not contaminated. To maintain the original pixel value, the selection of the threshold value is crucial. Generally speaking, its calculation formula is based on the average difference. After experimental verification, the sharpness of the image has been improved, and some details can be retained.

SIFT feature extraction

Scale-invariant feature transform algorithm (SIFT)15 is a local matching algorithm that searches for key points in different scale spaces established by Gaussian blur functions. The algorithm is invariant to image attribute changes, including rotation, translation, size, and brightness.

SIFT feature extraction method16 generally divides the image into a grid with a uniform distribution of a certain size, and extracts one SIFT feature point from each grid. Then, the SIFT method is used as a feature descriptor for the point based on the statistical feature point domain gradient histogram. SIFT algorithm has strong rotation invariance and good feature distribution. In general, because the orientation of pixel points closer to the center has a significant impact on the main orientation of the component block, the weight of each pixel point decreases as the distance increases, using a Gaussian function. After obtaining the main direction of the sampling block, the main direction of each small block can be rotated with reference to the main direction of the sampling block it is located in, and grouped into a unified coordinate system. In this way, when calculating the gradient histogram of each sampling block, only the relative directions of the sampling points and feature points need to be considered, and the generated descriptor has rotation invariance.

The specific research content is as follows. The SIFT features of each sub frequency image in a multiscale space are obtained, and the SIFT features of each sub frequency image are extracted, or each sub frequency of each sub frequency image is separately classified. Finally, a multi classifier synthesis method is used to discriminate and fuse them. When using SIFT feature extraction, the first step is to construct a scale space. Scale space theory is an application of partial differential equations in image information processing models. Its establishment is a process of adjusting continuously changing scale parameters. In this process, the core calculation method of scale space is as follows:

$${\text{f}}_{\text{out}}=\text{G}(\text{x},\text{y},\text{z})*{\text{f}}_{\text{in}}$$
(1)

In Formula (1), \(*\) represents a convolution operation. If the output value is less than or equal to the maximum value of the sampled image, then \(\text{G}(\text{x},\text{y},\text{z})\) is defined as the scale space kernel.

Because in multiple scale spaces, critical points are composed of local minima in variable geometric spaces, it is necessary to test the critical points. To select the extreme point of the difference of Gaussians (DOG) function, each pixel point is compared with all its neighboring points. After the comparison is completed, those pixels that meet the maximum or minimum grayscale values in the current range are recorded. Taking the starting stage of an athlete as an example, the obtained characteristic points are shown in Fig. 3.

Fig. 3
figure 3

Effect of feature extraction.

Full size image

SIFT is a classic image feature extraction algorithm that aims to extract local feature points in an image. These feature points are highly invariant to image rotation, scaling, brightness changes, and perspective changes. The SIFT algorithm first detects extreme points in the image (i.e., stable points in the scale space), then fine-grains these points and further extracts their local feature descriptors. Each feature point is defined by its scale, direction, and gradient information of the local image area, thus ensuring the robustness of the feature.

Although the SIFT algorithm demonstrates strong invariance to rotation, scaling, brightness changes, and perspective changes in image feature extraction, it also has certain drawbacks:

  1. A.

    The SIFT algorithm is computationally complex, especially when handling large-scale data, and its high computational cost may affect real-time processing capability.

  2. B.

    SIFT’s feature point extraction is relatively sensitive to noise in the image, which may lead to unstable feature points and subsequently affect the accuracy of classification and recognition.

  3. C.

    SIFT performs poorly when processing low-resolution images, potentially failing to capture fine details, which could become a bottleneck in certain motion trajectory recognition applications.

To validate the advantages of the SIFT algorithm, we compared it with other commonly used feature extraction algorithms, including Harris corner detection and SURF (speeded-up robust features). The results indicate that although the SURF algorithm outperforms SIFT in computation speed, its stability under rotation and scale changes is relatively weaker and more susceptible to image noise. While Harris corner detection can quickly extract corner points, it only focuses on local corner features and lacks the global feature description capabilities of SIFT. Therefore, it performs less effectively than SIFT when handling complex motion data. Based on the experimental data in Table 1, we conclude that the SIFT algorithm is most suitable for feature extraction in motion trajectories in this study, as it provides more robust and accurate feature point extraction when dealing with motion images that involve rotation, scale changes, and complex background noise.

Table 1 Performance comparison of SIFT, SURF, and harris corner detection.
Full size table

SVM classification

After extracting image features, it is necessary to classify the extracted features. In this paper, the SVM algorithm is used to classify the extracted features17. The fundamental principle of SVM classifier18 is a simple and effective way to handle data imbalance, which is widely used. The mathematical essence of SVM training is to solve support vector coefficients. The fitness function is:

$${\text{f}}\left( {{\text{x}}_{{\text{n}}} } \right) = \sum\limits_{{{\text{m}} = 1}}^{{\text{G}}} {{\text{n}}_{{\text{i}}} {\text{n}}_{{\text{j}}} {\text{m}}_{{\text{i}}} {\text{m}}_{{\text{j}}} {\text{K}}\left( {{\text{x}}_{{\text{i}}} {\text{x}}_{{\text{j}}} } \right)} - {\text{m}} = 1\sum\limits_{{}}^{{\text{G}}} {{\text{n}}_{{\text{i}}} {\text{n}}_{{\text{j}}} {\text{i}}}$$
(2)

For linearly separable samples, the relaxation variable \(\text{b}\) can be introduced to construct a classification hyperplane. At this point, the objective function is:

$$\underset{n,m,b}{\text{min}}\frac{1}{2}{\left|w\right|}^{2}+C\sum_{i=1}^{n}{b}_{i}$$
(3)

In Formula (3), \(\text{C}\) is the penalty factor. When \(\text{C}=0\), it is a linearly separable problem.

For SVM classifiers, the selection of kernel functions is a key factor in determining their performance19. The selection of kernel functions has a significant impact on the effectiveness and accuracy of classification. In this paper, a radial basis function with strong nonlinear characteristics is selected to establish a feature classifier for motion recognition. The expression is:

$$\text{K}({\text{X}}_{\text{a}},{\text{X}}_{\text{b}})=\text{exp}\left(-\frac{{\left|{\text{X}}_{\text{a}}-{\text{X}}_{\text{b}}\right|}^{2}}{{\upsigma }^{2}}\right)$$
(4)

The radial basis function kernel SVM processing model has excellent small sample learning ability and generalization performance. However, in order to improve classification accuracy, it is necessary to adjust the model penalty parameter C and kernel function parameter σ to obtain more ideal detection results20. On this basis, by optimizing the parameters of the classifier model, the optimal recognition of the classifier is achieved, thereby improving the recognition accuracy of the classifier. At the same time, the problems of over learning and under learning are overcome, and the adaptive ability of the classifier is enhanced21. In order to optimize the classification effect, it is necessary to traverse different parameter combinations through grid search combined with cross-validation, evaluate the performance of each set of parameters on the validation set, and then select the optimal C and \(\upsigma\) values. C controls the classifier’s tolerance to errors, and \(\upsigma\) determines the influence range of the kernel function. By reasonably adjusting these parameters, the classification accuracy and generalization ability of the SVM classifier can be effectively improved, overfitting and under fitting problems can be avoided, and better image classification results can be obtained.

The improvements to the SVM model in this paper mainly focus on optimizing the model architecture, addressing the specific needs of motion trajectory recognition tasks, and incorporating ideas from neural networks, along with several innovative measures to enhance classification accuracy and model stability:

To address the computational efficiency issues of traditional SVM models when handling large-scale and complex motion data, this paper introduces a hierarchical SVM architecture, which decomposes the entire motion trajectory recognition task into multiple sub-tasks. First, the athlete’s video data is pre-processed to extract motion feature points using optical flow, and these feature points are then categorized based on different motion stages. Each motion stage classification task is handled by an independent SVM sub-model. This hierarchical structure enables a more refined identification of key features at different motion stages, avoiding the oversimplification of the traditional single SVM model when dealing with complex data.

Considering the highly nonlinear characteristics of motion data, the kernel function design of SVM is improved. Traditional linear kernel functions cannot effectively handle the nonlinear relationships in motion trajectories, so this paper adopts a dual-kernel SVM architecture, combining radial basis function (RBF) and polynomial kernels for feature mapping. In this way, the SVM model can perform classification in a higher-dimensional space, better capturing the nonlinear features in the motion data. The RBF kernel is used to capture local features of the motion trajectory, while the polynomial kernel describes the global changes in the motion process. The combination of these two kernel functions effectively enhances the model’s adaptability to complex motion trajectories, enabling more accurate classification when processing the steps and trajectories of different athletes.

At the same time, an adaptive learning rate mechanism is introduced in the SVM model. Existing methods typically use a fixed learning rate, which can lead to slow convergence or premature convergence in certain training regions. To optimize this, a dynamic learning rate adjustment method based on gradient descent is introduced, which dynamically adjusts the learning rate based on the current model’s error during the training process. This improves the convergence speed and classification accuracy of the model. The goal of this improvement is to reduce training time and enhance the model’s robustness to complex and noisy motion data.

Trajectory tracking

Target trajectory tracking is mainly used to determine the specific position of the target in each screen based on the motion trajectory of the target at a certain moment. The association between target localization is two important links between target localization and target localization, which can be achieved separately or jointly. In the first case, the possible positions of targets in each frame are first obtained through target detection methods, and then the association between targets is achieved through target tracking methods based on inter frame information between targets. For the latter, the region where the target is located and its corresponding relationship with the previous frame are obtained by iteratively updating the location of the target based on the information from the previous frames. Regardless of the method used, the goal is to express it in a concise form, such as a point, an outline, or an external area. Different representations can impose certain constraints on the way objects move.

Among them, target expression can be divided into two categories: overall expression and local expression. The overall expression of an object is a comprehensive simulation of a series of characteristics of the surface of the object, among which the numerical value of the origin pixel and the color histogram are two relatively simple and effective overall features. However, due to the single, low-dimensional nature of the original pixel values, the number of sampling points is too small to reflect the correlation between pixels well. In addition, when the object has a similar background color, the color histogram cannot fully utilize the spatial information of the object, which can make it difficult to accurately track the object under the influence of certain background factors. Meanwhile, the calculation amount of this method is also large. Image representation methods based on local surface features express local structural information in an image through the relationship between images in the image, which is more robust than changes in overall surface features. However, the computational complexity of this algorithm is large, and it is difficult to meet the real-time requirements.

In track and field track tracking, the apparent model of moving objects often changes due to changes in lighting, posture, and occlusion. Therefore, an adaptive apparent model representation and efficient search strategy are important for robust target tracking.

Experimental results and discussion

Data source and classification

The SVM algorithm requires manual feature extraction. This article divided the footwork characteristics of track and field athletes into four characteristics: left foot landing (L1), left foot in the air (L2), right foot landing (R1) and right foot in the air (R2). The 2021 Tokyo Olympic Games sprint video was extracted frame by frame to obtain 882 images, which were divided into training set and test set in a ratio of 3:6. Part of the data for the training set and test set is shown in Fig. 4.

Fig. 4
figure 4

Part of training set and test set. (a) Part of the training dataset. (b) Part of the test dataset

Full size image

Different classification algorithms were used to identify these four features, and the recognition effect of the footwork is shown in Table 2.

Table 2 Footwork feature recognition results.
Full size table

Overall, the effect of using SVM algorithm for track and field footwork feature recognition was relatively stable, and its recognition accuracy was higher compared to other classification algorithms, which could effectively extract features.

To better evaluate the robustness and accuracy of the model, accuracy, precision, recall, specificity, and F1 score were used as evaluation criteria in the experiment. The corresponding calculation formulas for the evaluation indicators are as follows:

$$\text{accuracy}=\frac{\text{TP}+\text{TN}}{\text{TP}+\text{FP}+\text{TN}+\text{FN}}*100\text{\%}$$
(5)
$$\text{P}=\frac{\text{TP}}{\text{TP}+\text{FP}}*100\text{\%}$$
(6)
$$\text{R}=\frac{\text{TP}}{\text{TP}+\text{FN}}*100\text{\%}$$
(7)
$$\text{specificity}=\frac{\text{TN}}{\text{TP}+\text{FN}}*100\text{\%}$$
(8)
$$\text{F}1=\frac{2\text{PR}}{\text{P}+\text{R}}*100\text{\%}$$
(9)

In Formulas (5–9), \(\text{TP}\) indicates that a positive class sample is predicted as a positive class number. \(\text{TN}\) represents the prediction of negative class samples as negative class numbers. \(\text{FP}\) represents the prediction of negative class samples as positive class numbers. \(\text{FN}\) represents predicting a positive class sample to a negative class number. The results of different characteristics are shown in Tables 3 and 4.

Table 3 Results of different characteristics.
Full size table
Table 4 Evaluation indicators for different characteristics.
Full size table

Considering the frame-by-frame movement trajectory, different models were applied to a real-time 3-min video to calculate the F1 Score, as shown in Fig. 5.

Fig. 5
figure 5

Comparison of different models applied to the 3-min video.

Full size image

Figure 5 shows the comparison of F1 Scores for different models applied to a 3-min real-time video. The data indicates that the SVM outperforms all other models in all four actions (L1, L2, R1, R2), with average scores of 0.894, 0.891, 0.896, and 0.911, respectively, significantly higher than the other models. The high precision and stability of the SVM model demonstrate its effectiveness in motion trajectory recognition and foot action classification, accurately tracking the athletes’ steps and movements. In contrast, the KNN model has lower F1 Scores, particularly for actions L2 and R2, with averages of 0.724 and 0.728. This is because KNN is more susceptible to noise interference when handling complex motion data, resulting in decreased classification accuracy. The Naive Bayes and Decision Tree models also show some variation, with the Decision Tree performing relatively well for L1 and L2 but underperforming for R1 and R2. The CNN model falls between SVM and KNN, showing more balanced performance for L1 and R2, suggesting an advantage in image feature processing but still not reaching the optimal level of SVM.

From the perspective of overfitting, while SVM achieves the best F1 Score in Fig. 5, it is also more prone to overfitting, especially when the training data is limited or the data distribution is too simple. SVM may overfit to noise in the training set, leading to a reduction in its generalization ability in real-world applications. Although KNN and Naive Bayes have lower F1 Scores, indicating poor performance on complex motion data, they might offer better generalization, particularly in cases of uneven data distribution or noise. The CNN model shows some advantages in image processing for actions L1 and R2, but it still does not surpass SVM in terms of accuracy. Therefore, when selecting a model, both its performance on the training set and its generalization ability in practical applications should be considered to avoid overfitting issues.

Verification of results

To verify the improvement effect of footwork on track and field sports, 10 school athletes from a certain school were taken as examples. The age of athletes was between 21 and 23 years old, with 6 males and 4 females, with a height of 170 cm to 174 cm for males and 162 cm to 165 cm for females. Their actions were standardized through the extracted features, and their changes before and after the standardization were compared. The motion trajectory state of some motions is shown in Fig. 6.

Fig. 6
figure 6

Part of motion trajectory.

Full size image

The motion coordinate trajectory before and after the specification is shown in Fig. 7.

Fig. 7
figure 7

Motion trajectory change.

Full size image

It can be seen that after the improvement, the linear track displacement and curve track displacement of track and field athletes on the X axis showed an upward trend. On the Y-axis, the linear trajectory displacement and the curve trajectory displacement showed a relatively stable state, basically floating around 0. The linear trajectory displacement and the curve trajectory displacement on the Z axis decreased.

The track and field performances of 10 athletes in the first 10 standardized tests were compared. Taking the 100 m dash as an example, from March 27 to 28, 2023, tests were conducted every hour from 9 a.m. to 11 a.m., and from 14 p.m. to 15 p.m. Using Huawei P30 phone to take photos, data on ten 100 m sprints per person were collected within two days, and the resulting mean variance is shown in Fig. 8.

Fig. 8
figure 8

Mean variance diagram of sports performance before and after standardization.

Full size image

From the mean variance diagram in Fig. 8, it can be seen that before athletes were standardized, their overall average performance was between 11.4 s and 11.8 s, while after the characteristic point standardization, their performance was between 10.95 s and 11.2 s, with a significant improvement, which verified the effectiveness of the method in this article.

After the test, we created questionnaires to test people’s acceptance of the method and conducted an extensive questionnaire survey.Using a combination of online and online methods, 500 questionnaires were distributed, with the questionnaire questions shown in the attachment, and 425 questionnaires were eventually collected. After removing the useless questionnaire, 413 valid questions were obtained. The survey results are shown in Table 5.

Table 5 Questionnaire results.
Full size table

According to the questionnaire, in track and field sports, the proportion of men was higher than that of women. The age of track and field athletes is mainly distributed between the ages of 15–30 due to the physical requirements of track and field sports. In the questionnaire, a survey was conducted on footwork, performance, and acceptability of this method. The results are shown in Table 6.

Table 6 Part of results of the questionnaires.
Full size table

From the survey results, it can be seen that over 80% of people believed that footwork and stride length have an impact on track and field performance. The survey results showed that if the standardized image processing method could improve track and field performance, most people were willing to accept the modified method, and the acceptance level of males was higher than that of females. This showed that the method in this paper can be effectively extended.

Conclusions

With the in-depth development of track and field sports, athlete’s footwork recognition and trajectory tracking are becoming increasingly important in the formulation of competition strategies. As computer image processing technology matures, median filtering and mean filtering can effectively improve its recognition effect. In this paper, SVM algorithm was used to study the movements and trajectories of athletes. The computational complexity of athlete footwork feature classification can be greatly reduced, and its classification accuracy and efficiency can also be significantly improved. The survey results indicated that after the implementation of the technology, there were no significant difficulties in the subsequent promotion, and relevant technologies could provide assistance for the development of track and field sports. Certainly there are also certain problems in the process of this study. The collection scale of the dataset still needs to be continuously expanded to enhance the objectivity of the conclusions. In future research work, it needs to be considered to expand the experimental dataset by increasing the number of samples and the types of track and field footwork movements, and further improvements should be made on the efficiency of footwork recognition and trajectory tracking to promote the healthy development of track and field sports.