A new Similarity Based Adapted Louvain Algorithm (SIMBA) for active module identification in p-value attributed biological networks

Abstract

Real-world networks, such as biological networks, often exhibit complex structures and have attributes associated with nodes, which leads to significant challenges for analysis and modeling. Community detection algorithms can help identify groups of nodes of particular importance. However, traditional methods focus primarily on topological information, overlooking the importance of attribute-based similarities. This limitation hinders their ability to identify functionally coherent subnetworks. To address this, we propose a new scoring method for graph partitioning on the basis of a novel similarity function between node attributes. We then adapt the Louvain algorithm to optimize this scoring function, enabling the identification of communities that are both densely connected and functionally coherent. Extensive experiments on diverse biological networks, including artificial and real-world datasets, demonstrate the superiority of our approach over state-of-the-art methods. By leveraging both topological and attribute-based information, our approach provides a powerful tool for uncovering biologically meaningful modules and gaining deeper insights into complex biological processes.

Introduction

Real-world data, such as data of social networks, biological networks and technological networks, are often characterized by complex structures and interactions. Graph structures can be used to represent these data by modeling entities as nodes and the relationships that link them as edges between these nodes. These graphs can be attributed by the nodes to model certain characteristics of the entities and/or by the edges to represent the characteristics of their relationships. Community detection aims to extract areas of interest from these graphs by grouping nodes using the information contained in the graph.

When detecting communities in graphs attributed by nodes, the aim is to group nodes that are densely connected and have similar characteristics. Methods with this objective must therefore find a functional combination of two criteria: the topological criterion and the node attribute similarity criterion. In the majority of studies, communities are defined by the density of their connections. This is the reason why the majority of community detection algorithms prioritize the topological criterion.

However, in certain scenarios, a single dominant criterion may not be sufficient to define a community structure. In bioinformatics, for example, active module identification (AMI) involves identifying functionally coherent subnetworks, or “modules,” within complex biological networks such as protein–protein interactions and gene regulatory networks. These modules consist of highly interconnected nodes (proteins or genes) that exhibit coordinated activity under specific conditions. By focusing on these functionally related groups of genes or proteins, researchers can uncover key biological processes and potential therapeutic targets. In practice, AMI algorithms assign activity scores to nodes on the basis of experimental data and then identify densely connected subnetworks with significantly higher activity scores than are expected by chance. The values associated with nodes can represent various biological measurements, such as gene expression levels, fold changes in expression between experimental conditions, or p values indicating the statistical significance of these changes. Traditional community detection algorithms encounter challenges in such cases because of the lack of a clear density-based criterion and the static nature of biological interaction networks.

In this paper, we address the challenge of community detection in node-attributed graphs, particularly in the context of active module identification (AMI) in bioinformatics. To do this, we introduce a novel similarity function between node attributes that we use to define a new scoring method for graph partitioning that captures the interplay between node attributes and the network structure. Additionally, we adapt the widely used Louvain algorithm¹ to incorporate this scoring function, enabling it to identify communities on the basis of both topological and attribute-based criteria. Our proposed method yields significant advancements in community detection for node-attributed graphs, particularly in the context of AMI. By considering both topological and attribute-based information, our approach can identify more accurate and biologically meaningful modules within complex biological networks. This paper is organized as follows: “Related work” section presents the state-of-the-art methods, “Definition of similarity” section introduces the various functions defined in this article, “Similarity-based clustering” section describes the methodology used to perform similarity-based clustering, “Experiments” section presents the results obtained, and finally, “Conclusion” section concludes this work.

Related work

Community detection

Networks are used to describe many different real-life situations², which means that community detection algorithms can provide solutions to many problems. As a result, there are many studies on the different types of existing algorithms and the various fields of application of these methods^3,4,5,6,7.

In our context, we focus on community detection in node-attributed graphs⁷. This particular category includes multiple approaches, such as edge weight modification according to node attributes^8,9,10, linear combinations of attributes and network topology^11,12,13,14, walk-based approaches^15,16, machine learning methods^17,18,19,20, detection of graph patterns^16,21,22,23 and the efficient extension of algorithms to nonattributed graphs^{12,14,24,25,26}.

Community detection, also known as graph clustering, has a fuzzy definition. According to the taxonomy of Getoor et al. (2005)²⁷, for node-attributed networks, clustering consists of detecting groups of nodes that share common characteristics regarding the attributes and positions in the graph. This definition gives priority to neither attributes nor positions. Thus, a group of highly connected and slightly similar nodes is a cluster, as is a group of poorly connected nodes with nearly identical attributes. This ambivalence in definition leads to confusion over the term “cluster”, which we will examine further in “Active module identification”. To our knowledge, all the algorithms cited above are based on a topological definition of a community (i.e., nodes that are more strongly connected to each other than to the rest of the graph) and use the attributes contained in the nodes to refine their choice.

Active module identification

In the study of biological processes, such as disease development or cell division, it is possible to quantify the molecular changes that occur. Traditionally, these measurements are analyzed via statistical methods to generate a score expressing the degree of involvement of each gene in the process under study. Unfortunately, by relying exclusively on the score of each gene, these methods fail to detect the combined actions of genes; i.e., they may miss groups of genes with low individual scores but whose combined action plays a key role in the process under study²⁸. Known interactions between genes can be represented as a graph, where nodes represent individual genes and edges represent the relationships between them. These relationships can be of various types, including regulation (where one gene promotes or inhibits the activity of another), binding (where gene products physically interact, as in PPI networks) and co-expression (where genes are expressed in similar patterns) among others. By combining gene scores with information from the gene interaction network, the biological data studied can be represented by node-weighted graphs in which the detection of active modules is akin to community identification. Methods for identifying such gene clusters are called active module identification methods (AMIMs)^29,30.

AMIMs can be classified according to the way they identify subnetworks. Using this criterion, it is possible to divide the methods into five main categories: greedy algorithms^31,32,33, random walk-based methods³¹, optimization algorithms^32,33,34,35, machine learning processes³⁶ and clustering algorithms³⁷. Interestingly, not all of these methods use the assigned graph directly to detect active modules^32,33,37. Some employ alternative representations, such as vector embeddings of the network’s topological information^31,34,35,36.

A few years ago, AMIMs were criticized for the method by which they considered the topology of the graph³⁸. In their study, Lazareva et al. compared the results of several methods applied to an original node-weighted graph with those obtained from permuted versions of the graph, where the degree of each node was preserved. They reported that most methods identified similar modules in both the original and permuted graphs, leading them to conclude that these algorithms primarily rely on node degree and fail to capture richer biological information encoded in the network’s topology. The study highlights DOMINO³⁷ as the most effective algorithm, among those studied, for mitigating this bias. DOMINO uses static modularity-based clusterings, such as Louvain algorithm¹, of the unweighted graph, termed “slices,” to capture the graph’s topological information. It then performs multiple hierarchical clustering to select interesting communities based on a user-provided set of potentially active genes. This observation tends to show that the use of a classical topological clustering algorithm can reduce the bias introduced by node degree.

In addition, the experimental study carried out by Guttiérrez et al. in 2014³⁹ highlights the fact that biological networks are not similar to other complex networks, moreover, the structure of communities is different. Thus, it is necessary to propose a method inspired by topological clustering algorithms and taking into account the specificity of biological communities.

Definition of similarity

Prerequisites

In this work, we focus on community detection in node-attributed graphs in which the node attributes represent the statistical significance of gene expression changes, quantified by p values (Definition 1).

Definition 1

(Undirected graph with p-value-annotated nodes) Let $G = (V, E, w)$ be a node-attributed undirected graph such that:

• $V = \{v_i\; | \;i \in \mathbb {N}\}$ is the set of nodes $v_i \in V$ of graph G with i as the node identifier.

• $E = \{(v_k, v_j)\; | \;v_k \in V, v_j \in V\}$ is the set of edges $e \in E$ of graph G.

• $\begin{array}{l|rcl} w : & V & \longrightarrow & [0, 1] \\ & v_i & \longmapsto & p_i \end{array}$ is a weighting function that associates with each node $v_i \in V$ a p value $p_i \in [0,1]$.

Similarity function

As mentioned in “Community detection” section, the most common definition of a community is a set of nodes that are strongly connected. When nodes contain attributes, these attributes are used to refine the grouping obtained from the graph topology.

In the case of AMI, a community is not always particularly dense. The nodes must be connected, but there is not necessarily a greater density within the community than in the remaining graph. Communities are characterized mainly by the similarity of the node attributes; i.e., two nodes belong to the same community if and only if their values are sufficiently similar and there is at least one edge between them. To obtain a nonambiguous definition, we now need to formally define the notion of “sufficient similarity”. To this end, we propose a new similarity function that considers the existence of an edge between two nodes, as well as the values included in these nodes. This function is defined for any graph whose nodes are weighted by a p value. If the considered graph is weighted by another type of value, a similarity function adapted to the data must be used.

Definition 2

(Similarity function) Given two nodes $v_1 \in V$ and $v_2 \in V$, the similarity function $f(v_1, v_2): V \times V \rightarrow \mathbb {R}^{+}$ is defined as follows:

$$\begin{aligned} f(v_1, v_2)= {\left\{ \begin{array}{ll} \frac{1 - |p_1 - p_2|}{p_1 + p_2},& \text {if } (v_1, v_2) \in E\\ 0, & \text {otherwise} \end{array}\right. } \end{aligned}$$

In the case of AMI, p values are characterized not only by their similarity but also by their size. Indeed, to be considered interesting, a p value must be small. This is why our similarity function favors p values that are both similar and small. The smaller and more similar the p values contained in two connected nodes are, the greater the value of the function.

The similarity function is therefore defined on the range $[0, +\infty [$.

This wide definition interval makes it difficult to maximize the function, so we propose a normalized version of the similarity function (Definition 3). We normalize our $[0, +\infty [$ similarity function to the interval [0, 1] using an exponential projection. This method offers the advantages of simplicity and independence from node p-values and their statistical distribution.

Definition 3

(Normalized similarity function) Given two nodes $v_1 \in V$ and $v_2 \in V$, the normalized similarity function $f_{norm}(v_1, v_2): V \times V \rightarrow [0, 1]$ is defined as follows:

$$\begin{aligned} f_{norm}(v_1, v_2)= {\left\{ \begin{array}{ll} 1 - e^{-f(v_1, v_2)},& \text {if } (v_1, v_2) \in E\\ 0, & \text {otherwise} \end{array}\right. } \end{aligned}$$

In statistical analysis, an interesting p value is less than or equal to 0.05. This threshold is arbitrary but widely accepted. Thus, by analyzing the variations in the similarity function, we can set a threshold to define sufficient similarity (Definition 4). As the function is nonlinear and not monotonous, this threshold is not a drastic restriction on the p values. When a p value threshold of 0.05 is chosen, the sufficient similarity threshold is set to 10, but a p value slightly higher than 0.05 that is associated with a much lower p value is still included in the threshold of the similarity function.

Definition 4

(Sufficient similarity) Given a previously chosen threshold $x \in ]0, 1]$ representing the maximum value of an interesting p value, the threshold $t \in \mathbb {R}^+$ determining sufficient similarity is defined as follows:

$$\begin{aligned} t = \frac{\displaystyle 1 - |x - x|}{\displaystyle x + x} = \frac{\displaystyle 1}{\displaystyle 2x} \end{aligned}$$

Thus, given two nodes $v_1 \in V$ and $v_2 \in V$, sufficient similarity is defined as follows:

$$\begin{aligned} f(v_1, v_2) \ge t \end{aligned}$$

The similarity function can be used to determine whether two nodes are similar enough to belong to the same community. To obtain the most interesting communities (i.e., the active modules), it is not sufficient to associate similar nodes; it is also necessary to maximize the score of the associations made by the community detection algorithm.

Community score

To rank communities and identify the best one, it is necessary to be able to assign each community a score (Definition 5). From a theoretical point of view, an ideal community contains very similar nodes and is very dense. Therefore, we need to combine these two factors, bearing in mind that the communities we are looking for are not necessarily dense: between two communities with the same similarity score, the denser one should be preferred, but density is not the overriding factor.

Definition 5

(Community score) Given a community $C = (V', E', w) \subset G = (V, E, w)$, the community score is defined as follows:

$$\begin{aligned} s(C) = {\left\{ \begin{array}{ll} \frac{\displaystyle |E'|}{\displaystyle maxEdges} \sum _{i \in \llbracket 1, |V'| \rrbracket } \sum _{j \in \llbracket i+1, |V'| \rrbracket } f_{norm}(v_i, v_j),& \text {if } |E'| \ge 1\\ 0, & \text {otherwise} \end{array}\right. } \end{aligned}$$

where:

• $f_{norm}(v_i, v_j)$ is the normalized similarity function.

• $maxEdges = \frac{|V'| (|V'| - 1)}{2}$ is the maximum number of edges.

With this definition, the maximum score is obtained by an ideal community.

To determine the value at which the score of a community can be considered good, an acceptable score (Definition 7) is defined. A good community should have a score at least equal to that of a community with the same number of edges and whose nodes have the top similarity (among the nodes with sufficient similarity according to Definition 4) with respect to the graph (Definition 6); i.e., the value of the top similarity depends on the input graph.

Definition 6

(Top similarity) Given that $G = (V, E, w)$ is a node-attributed graph, the top similarity is defined as:

$$\begin{aligned} ts(G) = Q3(\{f(v_i, v_j)\; | \;v_i \in V, v_j \in V, f(v_i,v_j) \ge t\}) \end{aligned}$$

where:

• $f(v_i, v_j)$ is the similarity function.

• t is the sufficient similarity threshold.

• Q3 is the third quartile.

Definition 7

(Acceptable community score) Given a community $C = (V', E', w) \subset G = (V, E, w)$ with $|E'| \ge 1$, the acceptable community score is defined as follows:

$$\begin{aligned} as(C, G) = {\left\{ \begin{array}{ll} \frac{\displaystyle |E'|}{\displaystyle maxEdges} ts(G),& \text {if } |E'| \ge 1\\ 0, & \text {otherwise} \end{array}\right. } \end{aligned}$$

where:

• ts(G) is the top similarity of the graph.

• $maxEdges = \frac{|V'| (|V'| - 1)}{2}$ is the maximum number of edges.

Graph partitioning score

To guide a partitioning algorithm, one needs to be able to order two communities to establish which of the two is the best. To do this, a partition score function is defined using the notions of the score and acceptable score of a community as defined previously (Definitions 5 and 7, respectively).

Definition 8

(Partitioning score) Given a partitioning $P = {C_0, C_1,..., C_n}$ of $G = (V, E, w)$, the partitioning score is defined as follows:

$$\begin{aligned} s(P, G) = \sum _{C_i \in P} as(C_i, G)s(C_i) \end{aligned}$$

where:

• $s(C_i)$ is the score function of a community.

• $as(C_i, G)$ is the acceptable score of a community in G.

Similarity-based clustering

Filtering

As the Definition 4 establishes a threshold, it is possible to use it to reduce the graph and thus perform the clustering step on smaller subgraphs. Applying the filter is not the same as selecting p values below the p value threshold used to calculate the sufficient similarity threshold, as explained in “Similarity function” section.

This reduction allows the overall algorithm to be more efficient in terms of time, memory and results. Reducing the graph to interesting nodes allows the clustering algorithm to focus on the parts of the graph that are worth clustering, saving time and memory and reducing the noise in the final result. The method for performing this filtering process consists of 3 steps.

• 1. Weight the edges of the graph via the normalized similarity function (Definition 3).

• 2. Select edges with a score above the normalized threshold (Definition 4 combined with normalization, i.e., $1 - e^t$).

• 3. Join the selected edges into a community via the Union Find algorithm⁴⁰.

Importantly, at this stage, the uninteresting nodes are removed from the graph, whereas the edges are not. The resulting subgraphs can contain bad edges as long as they are connected to a node with at least one good edge. In short, only nodes that have only bad edges are removed.

This step produces numerous subgraphs containing the active modules. These subgraphs contain all the nodes that have a good value and/or are directly linked to nodes that have a good value.

Clustering algorithm

Using the functions defined in “Definition of similarity” section, it is possible to define a clustering algorithm that prioritizes node similarity. The idea is to derive the well-known and efficient Louvain algorithm.

This greedy algorithm works by optimizing modularity⁴¹. This topological metric is well known in the field of community detection and is based directly on the number of edges present in the community. As explained in “Similarity function” section, this metric is not efficient in the case of AMI.

Algorithm 1

Pseudocode of Similarity-Based Louvain

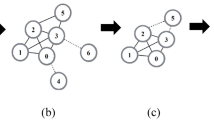
The algorithm (described in Algorithm 1) follows the same process as the Louvain algorithm, but instead of optimizing modularity, it seeks to optimize the partitioning score as defined in Definition 8. As the function to be optimized is nonlinear, the algorithm presents another difference from the original one. Whereas the Louvain algorithm sets the node in the community that increases the score to a maximum value, the algorithm presented here sets the node in the community that increases the score to a minimum value (Line 9 in Algorithm 1). That is, given all the node’s neighbors, the Louvain algorithm selects the one that allows the maximum increase in partition score, while SIMBA selects the one that allows the minimum increase. In fact, if we follow the policy of adding the best node, as suggested by the Louvain algorithm, we will be unable to add certain nodes. By adding the best node first, it becomes uninteresting to add another node that could have led to a more interesting community. Sometimes it may be necessary to make suboptimal choices to solve a global optimization problem.

Figure 1 demonstrates this difference in a minimal example. The aim is to select the entire graph as having good connectivity and only similar nodes (similarity between nodes is represented as a weight on the edge). Using the best-increase policy (left-hand side of the figure), it appears that node number 3 is left in its community. In contrast, the worst-increase policy (right-hand side of the figure) selects this node in the first phase of the algorithm, allowing it to become part of the final community.

Fig. 1

Minimal example illustrating the difference between the best-increase policy (Louvain) and the worst-increase policy (SIMBA).

The normalized similarity between nodes is taken as the edge weight to avoid calculating the same similarity value multiple times. This means that the second phase of the algorithm (line 13 of Algorithm 1) remains unchanged. As in the original algorithm, the new graph is created by summing the edge weights of the original graph to weight its edges.

General algorithm

Using the filter defined in “Filtering” and the clustering algorithm proposed in “Clustering algorithm” section, it is possible to define a general algorithm (Algorithm 2) for obtaining communities of interest in a node-attributed graph.

Algorithm 2

Pseudocode of SIMBA for active module identification

After the input graph is transformed into an edge-weighted graph via the similarity function (Definition 2), the edges of the graph can be filtered (line 2 in Algorithm 2), providing initial areas of interest in the graph. The clustering phase can then begin in the preselected areas. For each area, the first step is to determine whether it is worthwhile to run the clustering algorithm on it (line 6 in Algorithm 2). To do this, the number of nodes $|V'|$, the score s and the acceptable score as of the community are studied in light of Definition 9.

Definition 9

(Splittable community) A community $C = (V', E', w) \subset G = (V, E, w)$ is considered worth splitting if:

• $|V'| \ge 2*minimumNodes$ and $s(C) < as(C, G)$

• or

• $|V'| \ge 30*minimumNodes$

where:

• minimumNodes is a parameter set by the user, representing the minimum number of nodes required to obtain a community.

• s(C) is the community score.

• as(C, G) is the acceptable score of the community.

If it is interesting to perform the clustering algorithm, the community is then passed as the input to Algorithm 1 (line 7 in Algorithm 2). Otherwise, the initial area of interest is considered a good community and retained in the final result (line 13 in Algorithm 2). If Algorithm 1 is executed, the resulting new communities are compared with the original community, and if there is an improvement, they are retained. Otherwise, the original community is retained. This process is repeated until there is no further improvement.

A divisible community is therefore one that has at least enough nodes to be split into two parts but whose score is not sufficiently high. The second condition simply guarantees that in the case of a very large community, splitting will be attempted. In this work, it is assumed that a community that is 30 times larger than the minimum acceptable size is considered very large, but this value is arbitrary and can be modified. Indeed, very large communities may have scores that are biased relative to the others so that the first condition is not always sufficient. However, importantly, even if a community is considered divisible, this does not guarantee that divided communities will be retained. In fact, the new communities and the original community will be compared, and the best community will be retained.

Experiments

We next compare our method (SIMBA) with four AMIMs: Amine³¹, NetCore⁴², DOMINO³⁷ and GiGA⁴³. As each of these methods were designed to work on data similar to that tested in this work, they were all tested with their default parameters as defined in the articles from which they were derived. The first method takes a p value node-attributed graph as input and uses the network embedding to represent the information in the input graph. Then, a greedy algorithm performs AMI on the embedded data. The second method works directly on a p value node-attributed graph, where a directed heat diffusion model with a modified diffusion process determines the heat flow source or direction. The third runs a modularity-based clustering algorithm on an unattributed graph and then selects interesting modules using a user-supplied gene list. The last method takes as input an undirected graph and a sorted expression file. To obtain the modules an iterative process is used, starting from local minima, chosen using the expression file, the algorithm iterates through all the neighbors.

In addition to being compared with other AMIMs, our method is compared with the traditional p value selection method used in biology (i.e., all p values below the typical threshold of 0.05 are selected). This approach, subsequently referred to as the “baseline”, is commonly used in biological research.

Our algorithm requires two domain-specific parameters to be chosen by the user: the minimum number of nodes, minimumNodes (Definition 9), and the p value threshold used to calculate the sufficient similarity value, x, in Definition 4. The minimumNodes parameter must be chosen according to the specificity of the problem; as a general rule, communities with 3 nodes or less are never considered. Similarly, unless you want to obtain only large communities, it would be unreasonable to choose a high value. The x parameter is chosen in line with the statistical consensus that a p-value greater than 0.05 is not statistically interesting. This value is discussed in the Similarity function subsection just after definition 3. In the experiments described in this section, these parameters are set to 5 (empirically chosen to obtain relevant communities) and 0.05 (yielding a sufficient similarity of 10 in Definition 4).

To assess our algorithm’s performance, we used different types of simulated data presented in “Simulated dataset” section and a real-world biological graph, the results of which are presented in “Real graphs” section.

All the presented experiments were performed on a Precision 5820 Tower with 16 Intel Xeon(R) W-2245 CPUs with 125.5 GB of RAM.

Simulated dataset

Fully generated datasets

To our knowledge, there are no labeled datasets for AMI, so the algorithm was tested on simulated graphs. The graphs and their attributes were generated by following the method presented by Robinson et al. 2017⁴⁴, and the graph structure was generated via a Barabási-Albert model⁴⁵. The node attribute p values were generated according to a random uniform distribution between 0 and 1 on the nodes that were not in the active modules and a random continuous truncated normal distribution centered on 0, with a standard deviation of 0.05, truncated at 0 inside the active modules⁴⁴. Robinson’s methods were used to construct the ground-truth modules, beginning with randomly chosen starting nodes and adding random nodes in a randomly selected order (between 1 and 4) in the neighborhood of the starting node.

The results presented in this section were obtained from five different datasets (Supplementary Table S1). The first four datasets are composed of networks of 1000 nodes with one, two, three and ten modules of true hits, respectively, each module containing ten nodes. The fifth dataset is composed of networks of 6344 nodes matching the number of nodes present in the rewire dataset with a 0.99 cutOff presented in “Rewire datasets” section. The results obtained on it are used to intuitively show the differences among the various types of generated topologies presented in this work. As these datasets were composed of simple graphs, they were tested with Louvain clustering alone (i.e., the clustering algorithm was directly applied to the whole graph).

All the results presented in this work are evaluated according to the normalized mutual information (NMI) score and the binary F1 score (bF1). The binary F1 score (bF1) is calculated by merging all the modules into one and calculating the traditional F1 score for this binary-labeled community: 0 if the node is not in an active module and 1 otherwise. This score represents the number of well-extracted nodes in the graph.

We use two different calculation methods for each score. For NMI and bF1, the scores are calculated for all the communities returned by the algorithms studied. For NMI at k and bF1 at k, the scores are computed on the k best communities returned by the algorithm, where k is the number of communities in the ground truth. In this last calculation method, the communities are ranked via the method provided by the algorithm tested if possible; otherwise, the communities are ranked via the score proposed in Definition 5.

The results show that the proposed method outperforms the state-of-the-art methods, in term of NMI, on simulated 1000-nodes graphs, especially on the most complex dataset composed of 10 different modules to identify (Table 1 and Fig. 2). On the easiest dataset, the one composed of a single true hit module of size ten, SIMBA achieve significantly better results than other methods, including the baseline method traditionally used by biologists (Supplementary Table S2 and Supplementary Fig. S1). This baseline method has difficulties highlighting the nodes included in the true hit module and is, by design, unable to identify multiple groups of interesting nodes. It is not surprising that the NMI score is modest when several modules have to be identified. However, even compared to methods designed to highlight multiple modules, our method demonstrates significant better results (Supplementary Tables S3 and S4 and Supplementary Figs. S2 and S3).

Table 1 Results obtained on simulated graphs Ten clusters dataset in terms of the normalized mutual information (NMI), binary F1 score (bF1), normalized mutual information at k (NMI at k), binary F1 score at k (bF1 at k) and execution time (t in seconds). Results in bold are best column by column.

Fig. 2

Boxplot presenting the NMI obtained by each algorithm on the Ten clusters dataset.

The results of Table 2 and Fig. 3 show that for larger datasets, the results of the majority of methods decrease significantly, and their execution times become excessively long. The proposed method is not strongly impacted by those phenomena. This is important because, concerning AMI, the involved graphs have many nodes.

Table 2 Results obtained on simulated graphs Medium dataset in terms of the normalized mutual information (NMI), binary F1 score (bF1), normalized mutual information at k (NMI at k), binary F1 score at k (bF1 at k) and execution time (t in seconds). Results in bold are best column by column.

Fig. 3

Boxplot presenting the NMI obtained by each algorithm on the Medium dataset.

One of the strengths of SIMBA is that it does not require the number of communities to be known in advance. Supplementary Table S5 shows the evolution of the number of communities found via our similarity-based clustering method as a function of the input graphs. The proposed method succeeds in determining a number of communities close to that present in the ground truth. Moreover, the results show that the full output of the proposed method is worth considering, i.e., that the metrics at k are not representative of the method’s effectiveness.

Rewire datasets

The experiments and the literature show that the topology of the graph generated by Robinson’s method is too far removed from that of a real biological network. As it is very difficult to find real labelled networks, we decided to generate graphs that were more realistic in terms of their topology. To achieve this objective, the datasets used in this subsection were derived from real protein–protein interaction (PPI) networks. The random rewire model⁴⁶ was a good candidate for generating realistic graphs^38,47. Using such models, which take a real PPI network as input, we generated graphs with a more realistic topology. The values of the nodes were always generated via the normal distribution presented in “Simulated dataset” section.

The results presented in this section were obtained from two rewire datasets, generated from PPI networks downloaded from the STRING database⁴⁸ (version 11.5) with a cutoff of 0.99 and 0.80. The two datasets obtained are composed of 100 graphs with, respectively, 6344 nodes and 10 communities of 10 nodes and 14,219 nodes with 50 communities of 15 nodes (Supplementary Table S6).

The dataset with a cutoff of 0.99 had the same number of nodes and the same number of communities to find as the fully generated dataset (Medium dataset, results presented in Table 2). The objective was to confirm that the topology of a fully generated dataset is not equivalent to that of a real PPI graph.

The results presented in Supplementary Table S7 and in Supplementary Fig. S4 show that although the fully generated Medium dataset and the Rewire on human with 0.99 cutoff rewiring dataset appear to have the same characteristics, they are sufficiently dissimilar that they yield different results with all the algorithms. Indeed, the graph topology generation method is different, and it appears from the results that the rewire dataset derived from the real PPI generation method seems to be more difficult to process for all the algorithms tested.

Table 3 show that for the rewiring structure, which is closer to a real biological network structure, the proposed method better extracts the community structure even when the results are analyzed at k (Supplementary Fig. S5). Moreover, in Table 3, it appears that NetCore fail to perform on real-world-like data. In contrast, SIMBA performs well on those data and maintains an execution time that is correct for real-lab usage.

Table 3 Results obtained on simulated graphs Rewire on human with 0.80 CutOff in terms of the normalized mutual information (NMI), binary F1 score (bF1), normalized mutual information at k (NMI at k), binary F1 score at k (bF1 at k) and execution time (t in seconds). Results in bold are best column by column.

The results obtained on the dataset with a cutoff of 0.99 (Supplementary Table S7 and Supplementary Fig. S4) show that the decrease in performance of the state-of-the-art methods is not only due to the increase in graph size, and confirms that SIMBA does not show such a decrease on networks close to biological reality.

Simulated value dataset

The experiments in “Fully generated datasets” section use fully generated data. Those in “Rewire datasets” section use a realistic topological graph with simulated values. This subsection uses real topological graphs with simulated, realistic values.

To validate our module-detection algorithm, we simulated RNA-seq datasets with predefined differentially expressed gene modules. Gene sets were selected from MSigDB C2-CP: KEGG MEDICUS Version v2023.2.Hs⁴⁹. We selected five gene sets: M47840, M47744, M47495, M47715, and M47605 and applied fold changes of 1, 2, 5, 10, and 15, respectively (Supplementary Table S8). Stochastic variability was introduced to mimic biological noise. In silico RNA-seq reads were generated using the polyester package (v1.42)⁵⁰ and the Gencode v38 transcriptome reference⁵¹. Two experimental groups (treatment and control), each with three replicates, were simulated. Fold changes were applied to treatment group transcripts, and count matrices were generated for each sample. To minimize redundancy, one representative transcript per gene was retained. Differential gene expression analysis was performed with EdgeR v4.4⁵² using default parameters which resulted in LogFC for each gene and the associated p-value.

The value associated with the node are obtained from the simulated RNA-seq dataset and the graph structure is that of a real PPI graph taken from the STRING database⁴⁸, version 12.0.

The results presented in Supplementary Table S9 are computed on a graph of 12319 nodes and 132375 edges with 5 communities of 9, 14, 23, 6 and 10 nodes to be found.

The results presented in Supplementary Table S9 show that the proposed methods outperform the other methods by obtaining satisfying results in an execution time suitable for real laboratory applications.

However, as with the other methods, SIMBA’s performance declined. The analysis of the results revealed that SIMBA identified 36 communities with an average size of 6.95 nodes, totaling 250 nodes. In comparison, Amine detected 700 nodes across 123 clusters, DOMINO identified 246 nodes within 14 clusters, and GiGA found 233 nodes distributed in 33 clusters. Over-identification in most methods likely results from simulating RNA-Seq data, which naturally exhibits high variability. Consequently, although the ground truth comprises just 71 nodes, many more are flagged as significantly differentially expressed by the differential expression analysis pipeline. Specifically, 576 genes were associated with a p-value lower than 0.05. Despite this, all methods except Amine still outperformed a standard p-value-driven analysis in terms of gene count. Among the tested methods, NetCore stands out, identifying only 55 genes in 2 clusters, with just 15 belonging to the ground truth, resulting in a precision of 0.27. In comparison, SIMBA achieves a precision of 0.22, with 56 out of its 250 identified genes matching the ground truth. Moreover, SIMBA outperforms other methods in terms of NMI and F1-score, achieving 0.255 and 0.29, respectively.

For example, if we visualize the 23-node ground truth module of the Simulated value dataset with the STRING database⁴⁸, we obtain Fig. 4. To maximize connectivity, it is not surprising that SIMBA has identified two modules here. Indeed, by looking at the ground truth module it appears that the right part is dense while the left part is more sparse. To maximise the connectivity part of the scoring function, it is more interesting to create two modules, one highly connected (red box in Fig. 4) and one more sparse (orange box in Fig. 4).

Fig. 4

Module of 23 nodes contained in the Simulated value dataset ground truth. The boxes show the distribution of nodes in SIMBA-identified modules.

Getting a closer look to the SIMBA’s identified modules, it appears that some nodes are added (Supplementary Fig. S6 and Supplementary Fig. S7). Only one node is added to the first module (Supplementary Fig. S6): NCKAP1L. This node is strongly connected to the module (11 edges). So, even though its p value is “high” (0.075), it makes sense to add it to the community. For the other module, three nodes are added: RAB4A, SCAMP2 and CCDC120. These three nodes have low connectivity with the module (1 or 2 edges) but have p-values below 0.05. Given the low overall connectivity of this module, the algorithm tried to maximize the p-value term of the score.

Real graphs

To evaluate our novel module-detection algorithm on real biological data, we applied it to an RNA-seq dataset from a published study⁵³ investigating the geroprotective effects of Cmpd60, a selective HDAC1/2 inhibitor, on aged mice across three organs: heart, kidney, and brain. The original study focused on differential gene expression (DGE) analysis to identify changes in key biological processes associated with healthy aging, including reduced fibrosis, improved cardiac contractility, and attenuation of dementia-related gene signatures. While DGE analysis typically generates a list of individual genes without distinguishing functional relationships, our approach identifies gene modules, enabling insights into underlying networks of functionally related genes and pathways. As in the reference study, RNA-seq data from each organ were analyzed, and the top six modules (Modules 0 to 5) were annotated using Gene Ontology (GO)^54,55 and KEGG databases^56,57,58, facilitating direct comparisons with the results of the original study.

Kidney In the kidney, modules were enriched for processes aligning with the anti-fibrotic and pro-longevity effects reported in the reference study. Module 3 prominently featured proteostasis-related pathways (Supplementary Table S10), including ubiquitin-dependent protein catabolism⁵⁹. Module 4 was enriched in integrin-mediated signaling and cell-matrix adhesion pathways⁶⁰, consistent with the observed reductions in epithelial-mesenchymal transition and fibrosis following Cmpd60 treatment. Additional modules, such as Modules 0 and 5, highlighted translational machinery, while Modules 1 and 2 were enriched for steroid and cholesterol biosynthesis pathways (Supplementary Table S10), likely reflecting ancillary or background processes.

Brain In the brain, module analysis revealed networks consistent with the reference study’s focus on mitigating dementia-related processes. Module 0 showed strong enrichment for oxidative phosphorylation pathways and neurodegenerative disease-associated pathways, including Parkinson’s, Alzheimer’s, and Huntington’s diseases (Supplementary Table S11). This is consistent with the reported down-regulation of dementia-associated genes by Cmpd60 and suggests that mitochondrial and metabolic adjustments contribute to neuronal resilience⁵³. Module 1, enriched for glutamatergic synapse and long-term potentiation pathways, underscored neuronal communication and synaptic plasticity⁶¹, potentially reflecting enhanced cognitive function. Other modules highlighted general cellular functions, such as RNA polymerase activity (Module 2) and integrin-mediated signaling (Module 3), as well as stress-response pathways (Module 5), supporting a broader framework of neuroprotection (Supplementary Table S11).

Heart In the heart, our modular analysis identified networks associated with improved cardiac function. Module 1 was enriched for integrin-mediated signaling, cell-matrix adhesion, and angiogenesis-related pathways, which may enhance vascular structure and tissue integrity⁶². These findings correlate with the improved contractility and relaxation reported in the reference study⁵³. Module 5 showed enrichment in oxidative phosphorylation and energy metabolism pathways (Supplementary Table S12), implicating enhanced mitochondrial function in improved cardiac performance⁶³. Other modules, such as Module 0 (oxidative stress reduction) and Modules 2 to 4 (epigenetic and nuclear transport processes), likely represent foundational cellular mechanisms supporting long-term cardiac improvements^64,65.

Module identification facilitate underlying biological processes From the preceding results, we selected Module 3 and Module 4 for the kidney, Module 0 and Module 1 for the brain, and Module 1 and Module 5 for the heart. Enrichment of the selected modules was performed using gProfiler⁶⁶ and visualized through Cytoscape 3.10 (cytoscape.org). Enrichment analyses incorporated the GO Biological Process and Molecular Function databases, applying a Benjamini-Hochberg FDR threshold of < 0.05 and we retained only gene sets comprising 10 to 5000 genes. To enable visualization in Cytoscape’s Enrichment Map application, a GMT file was generated, with FDR q-value cutoff of 0.05. Our findings highlight pathways uniquely enriched in specific organs-for instance, Ubiquitin Protein Transferase Activity in the kidney, Postsynaptic Neurotransmitter Receptor Activity in the brain, and Growth Factor Binding in the heart. Conversely, some pathways were shared across organ systems, such as Integrin Binding in the kidney and heart, and the NADH metabolic pathway in the brain and heart (Fig. 5). These shared and distinct enrichment show the modular regulation of biological processes across tissues.

Fig. 5

EnrichmentMap of Gene Modules Across Organs Network diagram showing enriched pathways in selected modules (two per organ) from kidney (green), brain (blue), and heart (yellow). Node size reflects gene count, and gray edges denote shared genes or functional relationships.

Our module-based analysis provides a modular perspective on biological processes under specific conditions. By organizing genes into co-expression modules, we identified coordinated activities within pathways and molecular networks that are often overlooked by conventional gene-by-gene differential expression analyses. This approach elucidates the interconnected biological processes influenced by Cmpd60 and the mechanisms driving its beneficial effects on aging-related pathologies across multiple organs.

Conclusion

This paper introduces a novel approach to community detection in node-attributed graphs, which is specifically tailored for active module identification (AMI) in bioinformatics. By leveraging a novel scoring function for graph partitioning that considers both topological and attribute-based information, we develop a modified Louvain algorithm capable of identifying communities that balance connectivity and attribute similarity.

Our method offers a significant advantage over traditional community detection techniques by providing a more nuanced approach to community identification. It enables the discovery of communities that may not be apparent when only topological information is considered. In addition, the incorporation of a rigorous similarity function ensures that the communities identified are both cohesive and biologically significant.

A key strength of the SIMBA method is that it doesn’t require pre-specification of the number of communities, nor does it require determining a threshold beyond which the identified modules are no longer relevant. While other methods may be more effective when the number of modules is known beforehand and only the top-ranked modules corresponding to that number are considered, Simba imposes no such constraint and achieves superior performance across diverse datasets when considering all identified modules.

The proposed method has been extensively evaluated on both simulated and real-world biological datasets and has demonstrated superior performance compared with existing AMIMs. Its efficiency and scalability make it a valuable tool for obtaining novel insights into complex biological processes.

Future research directions could involve the exploration of more sophisticated scoring functions, the incorporation of domain-specific knowledge and the integration of advanced machine learning techniques to improve the identification of complex patterns and relationships within networks. This could lead to the development of more powerful and versatile community detection algorithms with applications beyond bioinformatics.