Abstract
This paper introduces a new design technique for Gysel power dividers (PDs) in substrate-integrated waveguide (SIW) technology, suitable for both equal and unequal power division. The method tackles the usual challenges linked to the cutoff frequency and line-width constraints, which often prevent direct application of standard Gysel formulas in SIW-based designs. By deriving new equations, we can achieve any power split while keeping the line width and cutoff frequency constant. Analytical models at Ku-band frequencies confirm this approach for both equal and unequal splits, and two SIW-based PDs operating at 15 GHz are designed and simulated. Moreover, we fabricated a prototype for the equal-power case to validate the design. Measured results show an isolation above 22 dB at 15 GHz, a return loss better than 10 dB at each port, and a 2.44 dB insertion loss, all closely matching the simulated data. This demonstrates the effectiveness of the proposed design approach.
Similar content being viewed by others
Introduction
Power dividers (PDs) are one of the essential components of microwave communication systems. They are usually needed in radar systems, phased array antennas, and wireless communication networks such as 5G, where requirements include equal and unequal power division with high port isolation. The PD is also required for satellite communication and high-power amplifier networks, supporting high-power handling specifically in frequency bands like Ku-band. The first Wilkinson PD was proposed in the year 1958. It provides good isolation between output ports, and all the ports are matched at the same time, but it is not good for high-power applications because there is no path to transfer the heat to the ground. The Gysel power divider (GPD), an extended form of Wilkinson PD, is well-suitable in applying high power division, as the ground is directly linked to the isolation resistors to allow for efficient ground absorption of heat.
Over the past few decades, researchers have made significant advancements in developing power dividers (PDs) by introducing modifications to the original Wilkinson PD and Gysel PD. These modifications involved the utilization of strip lines, microstrips, and waveguides. In1, an effort to enhance the power handling capability, a microstrip-based GPD was proposed, which incorporated arbitrary terminated impedance. To improve the performance of GPDs further, equivalent design methods for arbitrary power division ratios were proposed2. Multi-layer and multi-section techniques were used to achieve wide bandwidth and high isolation3. Another study demonstrated a combined Gysel-Wilkinson PD for arbitrary power division ratios4. Power handling capabilities were enhanced in a microstrip GPD with innovative thermal designs5. Filtering power dividers are proposed using a particle swarm optimization algorithm, a triple-mode resonator, low-pass filter integration, coupled lines with large input impedance, and isolation bandwidth in6,7,8,9.
Power divider integrated with coupled lines enabled advanced designs for LTE and GSM applications8. Another work demonstrated a PD design with an enhanced isolation network for wideband applications9. With an amplitude imbalance of 0.7 dB, a phase imbalance of \(10^\circ\), and an insertion loss of 0.6 dB, a metamaterial-based eight-way equal PD is developed in10. Frequency reconfigurable PDs have been developed by employing reconfigurable microstrip transmission lines11, \(\pi\)-shaped resonators12, and switchable LC circuits13. Designs incorporating multi-band operation for 5G applications have also been reported in14. Reconfigurable PD with compact design is presented in15.
However, it is worth noting that microstrip technology encounters limitations when operating at higher frequencies and when handling high power. These limitations primarily arise from high losses, crosstalk, and a relatively low power handling capacity. A dielectric resonator(DR) based filtering out-of-phase PD is developed for dual-band application in16. Since DRs are nonplanar resonator structures not suitable for compact design. A Ka-band Gysel PD was designed using rectangular waveguides in17, and by using E-plane rectangular waveguides in18. Waveguides are good for high-power handling but at the same time they are nonplanar and bulky, and fabrication is not easy. Substrate integrated waveguides (SIW) have recently become very popular as they can handle high power and have planar structures.
Researchers have made significant progress in the development of SIW-based power dividers, primarily categorized as T-junction19 and Y-junction PDs20. To reduce the size of these power dividers, a multi-layer approach21 and a planar SIW structure has been proposed22. An eight-way multilayer SIW-based power divider is developed with the help of a metallic waveguide for THz application in23. An equal-width SIW-based Gysel PD for X-band application is presented in24. Another notable development is the introduction of an air-filled SIW-based PD with a broadband 10 dB impedance and isolation bandwidth, which has been discussed in terms of power handling capability and thermal behavior25. However, these existing PD designs lack isolation analysis between the output ports and face challenges in achieving simultaneous matching of all ports. Designing a power divider requires incorporating transmission line sections with different impedances and widths. However, altering the width of an SIW to achieve the desired impedance can inadvertently impact the cutoff frequency, rendering the overall circuit non-functional. To overcome this limitation, the concept of a half-mode substrate-integrated waveguide (HMSIW) is proposed in the literature. A previous study reported an HMSIW power divider with an isolation network utilizing microstrip components26. In this design, the input line of the PD consisted of a complete SIW section, while the two output/distribution lines were composed of half-mode SIW sections. However, the use of HMSIW is limited to substrates with a thickness less than \(\lambda _g /10\), restricting its applicability to higher frequencies. Additionally, any discontinuities introduced during the fabrication or manipulation of HMSIW-based structures may result in radiation loss27. Moreover, the microstrip-based isolation network may not be as effective at higher frequencies. No Gysel PD using full SIW technology for arbitrarily selected power division has been documented in the literature as far as the authors are aware.
This research introduces a novel approach to designing Gysel PDs with equal and unequal power division ratios in SIW technology, addressing key limitations of prior works. Providing a foundation for power dividers with any desired ratio at a specific frequency. Analytical models at microwave frequencies validate the theoretical approach. SIW-based Gysel power dividers with both equal (\(K^2=1\)) and unequal (\(K^2=2\)) power divisions were designed and simulated at 15 GHz, with simulation results confirming the theoretical analysis. Stepwise instructions for designing SIW-based power dividers are included. A physical prototype of an equal power division GPD was fabricated, and S-parameter and phase difference measurements were conducted. These experimental results closely align with the theoretical predictions, demonstrating the effectiveness of the proposed design methodology.
Design of gysel PD for SIW technology
This section deals with deriving design equations required to develop equal/unequal PD. As the SIW width must be the same throughout the PD circuit to maintain the same cutoff frequency, the derivation assumes equal width of the SIW line sections.
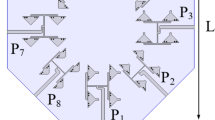
Schematic of a gysel power divider
Figure 1 describes the block diagram of the proposed Gysel PD.
Port 1 serves as the input terminal, while ports 2 and 3 act as the two output terminals. Each port and line within the PD have the same impedance of \(Z_0\). There are five lines in the presented model, each line having a different electrical length, and two resistors, each having the resistance value of R, are linked to the ground to provide isolation between ports 2 and 3; connecting these resistors to the ground makes this PD high power handling capable. The Gysel PD’s analysis is divided into two sections.
-
Input port to output ports power flow analysis.
-
Isolation analysis between output ports.
In further analyses, all the line impedances and isolation resistors are normalized w.r.t. \(Z_0\).
Power flow from the port-1 to the ports 2 & 3.
The purpose of the Gysel PD is to distribute the power from port 1 to ports 2 and 3 according to the desired ratio. The ideal behavior includes zero reflection from port 1 and no power dissipation in the isolation resistors. An equivalent circuit is depicted in Fig. 2 to analyze the power flow.
\(Z_{in1}\) and \(Z_{in2}\) in Eqs. (1) and (2) are calculated from Fig. 2.
\(Z_{in3}\) is obtained from Fig. 2 and \(Z_{in2}\) obtained in (2).
similarly \(Z_{in4}, Z_{in5}\), and \(Z_{in6}\) can be find
Since, power diving ratio \(k^2=\frac{P_2}{P_3}\)
from the Fig. 2\(I_2=V_2\) and \(I_3=V_3\)
Comparing (8) and (9), by replacing \(I_2=V_2\), \(I_3=V_3\), and \(V_2=kV_3\), equation (10) has been obtain.
After solving equation (10), equations (11), and (12) has been obtained.
Equation (12) is satisfied under the following two constrained \(\theta _2=\theta _4\) and \(\theta _3=\theta _1\)
After replacing \(\theta _4\) by \(\theta _2\), equation (11) is converted to equation (13)
\(Z_{in3}\) and \(Z_{in6}\) are connected in parallel combination& their equivalent impedance is the port impedance (\(1\Omega\)) in the Fig.2.
By solving (3), (6), and (14) following equation has been obtained.
To obtain \(\theta _1\) as a function of ’\(k^2\)’, equation (15) is solved using equation (13).
\(k\sin ^2\theta _1=2\cos \theta _1\cos \theta _2\)
\(k\sin ^2\theta _1=2\cos \theta _1\sqrt{1-\sin ^2\theta _2}\)
\(k^2\sin ^4\theta _1=4(1-k^2\sin ^2\theta _1-\sin ^2\theta _1+k^2\sin ^4\theta _1)\)
By solving equation (16)
From the conditions required to satisfy (12),
Using equations (13), (17), and (18), Table 1 shows the \(\theta _1\), \(\theta _2\), \(\theta _3\), and \(\theta _4\) values for different power division ratios (\(k^2=\frac{P_2}{P_3}\)).
Isolation Analysis of PD
Two isolation resistors are used to isolate the output ports from each other. Figure 3 presents an equivalent circuit for isolation analysis in which port 3 is excited and port 2 is short-circuited.
\(Z_{in7}\), \(Z_{in8}\) and \(Z_{in9}\) are obtained from Fig. 3 and given in (21), (22) and (24), respectively.
Similarly, from Fig. 3\(Z_{in10}\), \(Z_{in11}\) and \(Z_{in13}\) can be found and given in equations (23), (24), and (25), respectively.
\(Z_{in12}\) will be same as \(Z_{in11}\) because the line required for calculating \(Z_{in12}\), is having length of \(180^\circ\).
\(Z_{in14}=\frac{Z_{in13}+j\tan \theta _1}{1+jZ_{in13}\tan \theta _1}\)
\(Z_{in14}\) and \(Z_{in9}\) are in parallel, and their equivalent impedance is equal to the normalized port impedance (\(1\Omega\)) shown in Fig. 3.
Using (22), (26), and (27), the equation for \(r_1\) and \(r_2\) can be simplified as follows.
Equation (28) holds true when the conditions given in equations (31) and (32) are satisfied. This results in isolation resistors having a value of \(2Z_{o}\). The final design equations are enclosed in boxes: equations (13), (17), (18), and (32). These equations can be used to design a power divider with any power division ratio at the desired frequency.
Analytical results at microwave frequency
In this section, the analytical results of Gysel PD with different power division ratios are presented at 15 GHz.
GPD analytical model results for \(k^2=1\)
Based on the theoretical analysis and calculated design parameters of an equal power dividing ratio \(k^2=1\). The electrical length of the lines from Table 1 and the values of isolation resistances are as follows:
The operating frequency for the analytical model is 15 GHz. Since the power dividing ratio \(k^2=1\) means 1/2 (-3 dB) power will go to each output port. Figures 4 and 5 show the analytical results of the equal Gysel PD.
GPD analytical model results for \(k^2=2\)
The power dividing ratio \(k^2=2\) means 1/3 (-4.7dB) of total power will go to port 2 and 2/3 (-1.7dB) of total power through port 3. Figures 6 and 7 show the analytical results of the unequal Gysel PD. The electrical length of the lines from Table 1 and the values of isolation resistances are as follows:
Implementation in SIW technology
In this section, the Implementation of equal (\(k^2=1\)) and unequal (\(k^2=2\)) Gysel PD are presented in SIW technology at a frequency of 15 GHz, in a circular ling topology, and their S-parameters and phase difference results are presented.
Equal gysel PD (\(k^2=1\)) at 15 GHz
Structure design
The structure of the proposed equal PD is shown in Fig. 8, implemented using SIW technology. The proposed PD is using substrate RT/duriod 5880 having a thickness of 0.508 mm and \(\epsilon _r = 2.2\). The structure is having 3 ports. Port-1 is the input terminal, while ports 2 and 3 are the output terminals. All the SIW lines are having equal widths so that it would not affect the cut-off frequency and impedance values remain the same for all SIW lines. The position of ports 3, 2 and isolating resistors are determined based on the \(\theta _1\), \(\theta _2\), \(\theta _3\), and \(\theta _4\) values obtained in the design of PD in SIW technology section. The physical length of SIW lines can be calculated using (33).
This PD consists of two isolating resistors of \(100\Omega\) each. To complete the closed loop topology, multiple sections of \(\lambda _g/2\) are added to \(\theta _1\), \(\theta _2\), \(\theta _3\), \(\theta _4\) and \(180^\circ\) lines. The via diameter and distance between two consecutive vias holes are taken as 1.5mm and 2.5mm respectively.
Simulation results of equal GPD
The HFSS (High frequency structure simulator) full wave simulator, based on the finite element technique (FEM), is used to design and simulate the design of the SIW PD for equal power division. Insertion loss for the frequency band from 14.5 to 15.5 GHz is nearly 0.78 dB. As a result of the insertion losses, both ports 2 and 3 receive a power of -3.8 dB each.
Figures 9 and 10 illustrate the E-field distribution of the Gysel PD with an equal power division ratio. The desired equal power ratio is achieved when input port 1 (Fig. 9) is exited with an input signal. Negligible power goes to the isolating resistors. The achieved high isolation between the output terminals of the Gysel PD with equal power division is validated by the absence of power transmission to port 3 or port 2 when port 2 or port 3 is excited with input power, respectively (as shown in Fig. 10).
The reflection coefficient(\(S_{11}\), \(S_{22}\), \(S_{33}\)), isolation (\(S_{32}\)), and transmission coefficients (\(S_{21}\) and \(S_{31}\)) shown in Fig. 11. All the reflection coefficients are below the 15 dB line around the center frequency of 15 GHz. Isolation is better than 20 dB for the operating frequency. The phase difference between the output signals at ports 2 and 3 is shown in Fig. 12 with a phase error of \(0.68^\circ\).
Unequal Gysel PD (\(k^2=2\)) at 15 GHz
Structure design
The location of ports 3 and 2 and isolating resistors are determined based on the \(\theta _1\), \(\theta _2\), \(\theta _3\), and \(\theta _4\) values obtained in the design of GPD in SIW section. The design of unequal GPD in SIW technology is shown in Fig. 13. The physical length corresponding to the electrical length of SIW lines can be calculated using (33). The PD consists of two isolating resistors of \(100\Omega\) each. To complete the closed loop topology, multiple sections of \(\lambda _g/2\) are added to \(\theta _1\), \(\theta _2\), \(\theta _3\), \(\theta _4\) and \(180^\circ\) lines. The via diameter and distance between two consecutive vias holes are taken as 1.5mm and 2.5mm, respectively.
Simulation results of unequal GPD
Since the power diving ratio \(k^2=2\) means 1/3 (-4.7dB) of total power will go to port 2 and 2/3 (-1.7dB) of total power through port 3. For this design insertion loss at center frequency is 1 dB. As a result of the insertion losses, port 2 receives a power of -2.5 dB, while port 3 receives a power of -5.5 dB. Figures 14 and 15 display the electric field distribution of the Gysel PD with an unequal power division ratio. The desired unequal power division is achieved when input port 1 is excited with an input signal. Negligible power is transmitted to the isolating resistors. High isolation is achieved as when port 2 or 3 is exited with input power (Fig. 15), with no power received at port 3 or 2 respectively.
The reflection coefficients (\(S_{11}\), \(S_{22}\), \(S_{33}\)), isolation (\(S_{32}\)), and transmission coefficients (\(S_{21}\) and \(S_{31}\)) are presented in Fig. 16. The reflection coefficient of ports 1 and 2 is below 20 dB at the center frequency. Isolation is better than 20 dB. The phase difference between the output signals at ports 2 and 3 is shown in Fig. 17 with a phase error of \(0.86^\circ\).
From the above theoretical and design study, the following are the steps for Gysel PD design at any desired frequency with an arbitrary power division ratio.
-
1.
Calculate the Width of SIW: Use the following equations (34) and (35) to determine the SIW width (\(W\)) required to support the desired operating frequency band28:
$$\begin{aligned} f_c= & \frac{c}{2\epsilon _r} \sqrt{\left( \frac{m}{W_{eff}}\right) ^2 + \left( \frac{n}{h}\right) ^2} \end{aligned}$$(34)$$\begin{aligned} W_{eff}= & W-1.08\frac{d^2}{s}+0.1\frac{d^2}{W} \end{aligned}$$(35)where, \(f_c\) = Cut-off frequency, \(W_{eff}\) = Effective width of SIW, W = Physical width of SIW, \(\epsilon _r\)= Relative Permittivity, d = via diameter, s = distance between to via holes.
-
2.
Calculate Physical Length of Transmission Lines (TLs): Choose the required power division ratio (\(k^2\)) and use equations (13), (17), (18), and (32) to determine the physical length (l) of all transmission lines. Take both the resistor values as \(2Z_0\) according to the derivation in design of GPD in SIW technology section.
-
3.
Measure TL Lengths: Measure the lengths (\(l_1, l_2, l_3, l_4, l_5\)) from the center of the port locations. If necessary, adjust these lengths by adding multiples of \(\frac{\lambda _g}{2}\) to make the structure physically realizable or design the closed-loop topology.
-
4.
Design SIW to Microstrip Line Transition: Design a transition from SIW to microstrip line to feed the power divider structure. This transition should be designed to smoothly match the characteristics of the SIW and microstrip line.
-
5.
Optimize PD Structure: Optimize the designed power divider structure to achieve the best performance in terms of return loss, isolation, and insertion loss parameters.
Results Of fabricated SIW equal GPD
To validate the proposed method, the SIW-based equal Gysel PD discussed in the equal Gysel PD section is fabricated on the Roger/duroid 5880 substrate, which has a thickness of 0.508 mm and a dielectric constant of 2.2. Two SMT resistors with each value of \(100 \Omega\) and three RF connectors having max. interface frequency of 18 GHz was carefully soldered to the structure to ensure proper functionality.
The fabricated prototype of equal GPD along with the measurement setup is presented in Fig. 18. To evaluate the performance of the fabricated equal GPD, the S-parameters were measured using a Keysight vector network analyzer (VNA).
The measured S-parameter results for the fabricated GPD prototype are presented in Fig. 19. Figure 19a–d illustrate the return loss at the input port (\(S_{11}\)), return loss at output port 1 (\(S_{22}\)), return loss at output port 2 (\(S_{33}\)), and the isolation between the output ports (\(S_{32}\)), respectively. These results demonstrate excellent impedance matching and high isolation, with the measured values closely aligning with the simulated performance, thereby validating the effectiveness of the proposed design. The transmission parameters are presented in Fig. 20. Figure 21 illustrates the phase difference between the signals at the two output ports, showing minimal deviation and indicating that the output signals are in-phase as intended with a phase error of \(2.9^{\circ }\) at 15 GHz, as measured in the experiment. The measurements show that insertion loss at the center frequency is 2.44 dB. In conclusion, the measured S-parameter and phase difference results are similar to the simulated results obtained during the design phase. A comparative analysis of the measured results with previously published works is also provided in Table 2. This comparison highlights that the proposed design offers competitive performance in terms of return losses, isolation, and insertion loss, while also providing the added advantage of design equations applicable for equal and arbitrary power division ratios and scalable design frequency.
Conclusion
The paper has proposed a novel approach for designing Gysel PD with equal and unequal power division in SIW technology for microwave frequencies. The design methodology takes into consideration of dependency of the cut-off frequency and impedance on SIW width, leading to the derivation of design equations that enable arbitrary power division ratio while maintaining a fixed-width line in adherence to SIW constraints. Analytical models were developed for equal and unequal power dividers at microwave frequencies. Additionally, two SIW-based GPDs were designed and simulated at the design frequency of 15 GHz. The simulation results demonstrated excellent performance. To confirm the practical feasibility of the proposed design, an equal power division GPD prototype was fabricated in SIW technology. The measured results are closely aligned with the simulated data, providing further evidence of the effectiveness and accuracy of the proposed design approach. The promising simulation and measurement results validate the proposed approach’s potential for designing GPD at any desired frequency in SIW.
Data Availability
All data generated or analysed during this study are included in this article.
References
Wu, Y., Liu, Y. & Li, S. A modified gysel power divider of arbitrary power ratio and real terminated impedances. IEEE Microwave Wirel. Compon. Lett. 21, 601–603 (2011).
Xia, B. et al. A new gysel out-of-phase power divider with arbitrary power dividing ratio based on analysis method of equivalence of n-port networks. IEEE Trans. Microw. Theory Tech. 69, 1335–1343 (2020).
Chen, H., Zhou, Y., Zhang, T., Che, W. & Xue, Q. \(n\)-way gysel power divider with arbitrary power-dividing ratio. IEEE Trans. Microw. Theory Tech. 67, 659–669 (2018).
Nemati, R., Karimian, S., Shahi, H., Masoumi, N. & Safavi-Naeini, S. Multisection combined gysel-wilkinson power divider with arbitrary power division ratios. IEEE Trans. Microw. Theory Tech. 69, 1567–1578 (2021).
Fu, C. et al. A gysel power divider/combiner with enhanced power-handling capability. Electronics11 (2022).
Mohammadi, M., Karimi, G. & Sarabi, H. G. Design of a microstrip wilkinson power divider using a low pass filter with the particle swarm optimization algorithm. Sci. Rep. 14, 17637 (2024).
Wang, D., Guo, X. & Wu, W. Wideband unequal power divider with enhanced power dividing ratio, fully matching bandwidth, and filtering performance. IEEE Trans. Microw. Theory Tech. 70, 3200–3212 (2022).
Moloudian, G. et al. Design and fabrication of a wilkinson power divider with harmonic suppression for lte and gsm applications. Sci. Rep. 13, 4246 (2023).
Liu, Y., Sun, S. & Zhu, L. 2\(n\)-way wideband filtering power dividers with good isolation enhanced by a modified isolation network. IEEE Trans. Microw. Theory Tech. 70, 3177–3187 (2022).
Zhou, Z. & Li, Y. \(n\)-port equal/unequal-split power dividers using epsilon-near-zero metamaterials. IEEE Trans. Microw. Theory Tech. 69, 1529–1537 (2021).
Zarghami, S. & Hayati, M. Narrow-band power dividers with wide range tunable power-dividing ratio. Sci. Rep. 12, 17351 (2022).
Abdipour, A. & Makki, S.V.A.-D. Miniaturized equal/unequal wilkinson power dividers capable of harmonic suppression utilizing microstrip \(\pi\)-shaped resonators modified by lumped elements. Sci. Rep. 14, 7337 (2024).
Zhan, W. L., Xu, J. X. & Zhang, X. Y. Low-loss reconfigurable power divider with arbitrary operating channels using switchable \(k\) inverters for antenna feeding network applications. IEEE Trans. Microw. Theory Tech. 70, 1789–1796 (2022).
Lee, S., Park, J. & Hong, S. Millimeter-wave multi-band reconfigurable differential power divider for 5g communication. IEEE Trans. Microw. Theory Tech. 70, 886–894 (2021).
Nair, R. G. Design theory of compact power divider with reconfigurable power division and negative group delay characteristics. Sci. Rep. 13, 7222 (2023).
Yu, W., Xu, L., Zhang, X. Y. & Chen, J. X. Dual-band dual-mode dielectric resonator filtering power divider with flexible output phase difference and power split ratio. IEEE Trans. Microw. Theory Tech. 70, 190–199 (2021).
Song, K., Yan, Y., Zhou, Y., Fan, M. & Fan, Y. Ka-band rectangular-waveguide gysel power divider with low insertion loss and high output isolation. Journal of Infrared, Millimeter, and Terahertz Waves 39, 996–1004 (2018).
Fahmi, M. M., Ruiz-Cruz, J. A. & Mansour, R. R. Design of gysel power combiners in e-plane rectangular waveguides. AEU-Int. J. Electron. Commun. 127, 153449 (2020).
Germain, S., Deslandes, D. & Wu, K. Development of substrate integrated waveguide power dividers. In CCECE 2003-Canadian Conference on Electrical and Computer Engineering. Toward a Caring and Humane Technology (Cat. No. 03CH37436), vol. 3, 1921–1924 (IEEE, 2003).
Hao, Z. ., Hong, W., Li, H., Zhang, H. & Wu, K. Multiway broadband substrate integrated waveguide (siw) power divider. In 2005 IEEE Antennas and Propagation Society International Symposium, vol. 1, 639–642 (IEEE, 2005).
Chen, H., Che, W., Wang, X. & Feng, W. Size-reduced planar and nonplanar siw gysel power divider based on low temperature co-fired ceramic technology. IEEE Microwave Wirel. Compon. Lett. 27, 1065–1067 (2017).
Khan, A. A. & Mandal, M. K. Miniaturized substrate integrated waveguide (siw) power dividers. IEEE Microwave Wirel. Compon. Lett. 26, 888–890 (2016).
Zhou, Y. et al. Novel sub-terahertz high isolation stacked-siw power divider. IEEE Transactions on Terahertz Science and Technology (2023).
Bharti, B. K. & Yadav, A. N. Siw based in-phase gysel equal power divider for x-band application. AEU-International Journal of Electronics and Communications155206 (2024).
Nguyen, N. H. et al. Fabrication-tolerant broadband air-filled siw isolated power dividers/combiners. IEEE Trans. Microw. Theory Tech. 69, 603–615 (2020).
Chen, H., Che, W., Wang, X., Zhou, Y. & Xue, Q. Development of compact hmsiw gysel power dividers with microstrip isolation networks. IEEE Access 6, 60429–60437 (2018).
Djerafi, T., Hammou, D., Wu, K. & Tatu, S. O. Ring-shaped substrate integrated waveguide wilkinson power dividers/combiners. IEEE Trans. Components Pack. Manuf. Technol. 4, 1461–1469 (2014).
Cheng, Y. J. Substrate integrated antennas and arrays (CRC Press, 2018).
Acknowledgements
The authors gratefully acknowledge the DST-FIST RF and Wireless Research Laboratory at the Department of Electronics and Communication Engineering, IIIT Allahabad for (Antenna Testing/Microwave Circuit testing/fabrication).
Funding
The work was sponsored by the Indian Institute of Information Technology, Allahabad, under the seed research grant project IIITA/RO/181/2022.
Author information
Authors and Affiliations
Contributions
Brij Kumar Bharti: Writing original draft, Visualization, Validation, Software, Methodology, Formal analysis, Conceptualization. Amar Nath Yadav: Writing original draft, review & editing, Supervision, Methodology, Project administration, Funding acquisition.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests. The corresponding author is responsible for submitting a competing interests statement on behalf of all authors of the paper.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Bharti, B.K., Yadav, A.N. A new design technique and realization of gysel power dividers in substrate integrated waveguide for Ku-band applications. Sci Rep 15, 10844 (2025). https://doi.org/10.1038/s41598-025-95799-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-025-95799-w