Introduction

The application of array antennas is very extensive, such as 5G communication1, radar detection2, intelligent transportation3, etc. However, such widespread applications are due to the fact that array antennas can effectively improve signal gain and quality, enhance anti-interference capabilities, and achieve high-precision positioning and detection. As everyone knows, array antennas with high gain and low sidelobe performance are key to achieving signal enhancement and anti-interference capability improvement in wireless communication systems. Previous studies have shown that achieving high gain and low sidelobe radiation performance of array antennas can be achieved by designing the array layout. Among them, optimizing the layout of array element directions is an effective design method. By reasonably adjusting the directions of each array element, not only can the maximum gain in the main radiation direction be increased, but also the sidelobe level in the main radiation direction can be suppressed, while limiting the cross-polarization gain4. Array antennas are divided into linear array antennas (LAA)5, planar array antennas (PAA)6, circular array antennas (CAA)7,8, and Elliptical array antennas (EAA)9, according to the arrangement of antenna elements. This article mainly studies linear array antennas.

Linear array antenna is a relatively basic and common type of antenna, which is composed of multiple antenna elements arranged and combined along a straight line10. Due to its simple geometric structure and wide range of applications, it has attracted extensive research from many scholars. Unfortunately, with the rapid development of wireless communication, radar detection and other technologies, traditional linear array antenna design methods often struggle to meet increasingly complex and diverse performance requirements. However, the emergence of optimization algorithms has brought new opportunities for the design of linear array antennas. By using advanced optimization algorithms, various parameters of the antenna can be more accurately adjusted. For example, particle swarm optimization(PSO)11, artificial bee colony (ABC) algorithm12, cat swarm optimization(CSO)13, spider monkey optimization (SMO)14, backtracking search algorithm (BSA)15, harmony search (HS)16, flower pollination algorithm(FPA)17, ant colony optimization (ACO)18, differential evolution (DE) algorithm19, dandelion optimization(DO) Algorithm20, modified reinforcement learning algorithm(MORELA)21, invasive weed optimization (IWO) algorithm22, grasshopper optimization algorithm(GOA)23, modified seagull optimization algorithm(MSOA)24, jellyfish search (JS) algorithm25, Archimedes optimization algorithm (AOA)26, etc. These optimization algorithms mainly optimize the spacing and excitation amplitude between antenna elements to achieve the goals of reducing sidelobe levels, improving antenna gain, and optimizing beam direction.

The Pelican Optimization Algorithm (POA)27 is a new type of optimization algorithm proposed in 2022, inspired by the behaviors of pelicans such as living and hunting in nature. Once proposed, this algorithm has been favored by many scholars due to its superior performance and has been applied in various fields such as heterogeneous wireless sensor networks28, microgrid energy management29, and automatic facial emotion recognition30. Regarding its shortcomings, such as premature convergence, the imbalance between exploration and exploitation, and lack of population diversity. Many scholars have proposed a series of improvement strategies and applied them in practical problems. As mentioned in reference31, The author proposes an improved algorithm called IPOA, which uses three different strategies during the exploration phase of POA, namely Self-knowledge movement, Member-based movement, Group-based movement, To update the position of Pelicans and improve the performance of POA during the exploration phase, and apply it to solve load scheduling problems; In reference32, in the development stage of POA, the author recalculates the Euclidean distance between members and prey, and then modifies its mathematical model to adjust the development stage of POA in discrete space. And the improved POA was applied to the dynamic reconstruction of photovoltaic arrays, resulting in a 30% increase in output power in shadow scenes. Various examples demonstrate that POA has superior performance in handling practical problems.

In response to the shortcomings of POA, this manuscript combines Logistic chaotic mapping33 and triangular walk strategy34 with POA to propose an algorithm called CTPOA and applies it to two types of synthesis problems in linear arrays: the first is an equidistant symmetric array, which maintains the phase of the excitation current at zero and obtains the desired directional pattern by optimizing the amplitude of the excitation current of the array elements; The second type is a non-equidistant symmetric array, which maintains the amplitude and phase of the excitation current of the array elements unchanged, and obtains the desired directional pattern by optimizing the spacing between the array elements. From the simulation data results, it can be seen that CTPOA has excellent advantages in optimizing array antennas. The other parts of this article are arranged as follows: Sect "Improved CTPOA" provides a detailed introduction to POA and its improvement points, while Sect "Benchmark function testing" evaluates the performance of CTPOA using testing functions and compares it with other algorithms. Then, in Sect "Pattern synthesis of linear antenna array", various examples of linear array synthesis were presented, and the CTPOA was used to optimize the excitation current amplitude of equidistant symmetric arrays and the element spacing of non-equidistant arrays. Compare the results with other natural evolution algorithms to evaluate the effectiveness of the CTPOA in synthesizing linear arrays. Finally, the conclusion is presented in Sect "Conclusions".

Improved CTPOA

This section provides a detailed description of POA and two improvement points, namely Logistic chaotic mapping and triangle walk strategy.

Original pelican optimization algorithm

Inspiration

As shown in the Fig. 1, the pelican is a large, long billed, social bird with a particularly large throat, resembling a bag, and usually feeds on fish. They often cooperate with each other in hunting. Once they identify their prey, they will fly down from high altitude, rush towards it, and then spread their wings on the water surface, forcing the fish to swim towards shallow waters, which is beneficial for them to hunt. The behavior and strategy of pelicans during hunting is an intelligent process that makes these birds skilled hunters. The main inspiration for the proposed POA design comes from modeling the above strategies.

Fig. 1
figure 1

Pelican hunting process.

Full size image

Mathematical model

The mathematical model of Pelican Optimization Algorithm is divided into three stages: initialization, moving towards prey stage, and spreading wings on water stage.

Initialization

The POA is a population-based algorithm, where pelicans are members of the population, meaning each pelican represents a candidate solution. Randomly initialize group members based.

on the lower and upper bounds of the problem using Eq. (1).

$${x_{i,j}}={l_j}+\operatorname{rand} \cdot \left( {{u_j} - {l_j}} \right),i=1,2, \ldots ,N,j=1,2, \ldots ,m$$
(1)

where \({x_{i,j}}\) is the value of the j-th variable specified by the i-th candidate solution, N is the number of population members, m is the number of problem variables, rand is a random number in interval [0, 1], \({u_j}\) and \({l_j}\) respectively represent the upper and lower position boundaries of the pelican.

The spatial position of pelicans is represented by Eq. (2).

$$X={\left[ {\begin{array}{*{20}{c}} {{X_1}} \\ \vdots \\ {{X_i}} \\ \vdots \\ {{X_N}} \end{array}} \right]_{N \times m}}={\left[ {\begin{array}{*{20}{c}} {{x_{1,1}}}& \cdots &{{x_{1,j}}}& \cdots &{{x_{1,m}}} \\ \vdots & \ddots & \vdots &{}& \vdots \\ {{x_{i,1}}}& \cdots &{{x_{i,j}}}& \cdots &{{x_{i,m}}} \\ \vdots &{}& \vdots & \ddots & \vdots \\ {{x_{N,1}}}& \cdots &{{x_{N,j}}}& \cdots &{{x_{N,m}}} \end{array}} \right]_{N \times m}},$$
(2)

where X is the population matrix of pelicans and \({X_i}\) is the i-th pelican.

The objective function is represented by Eq. (3).

$$F={\left[ {\begin{array}{*{20}{c}} {{F_1}} \\ \vdots \\ {{F_i}} \\ \vdots \\ {{F_N}} \end{array}} \right]_{N \times 1}}={\left[ {\begin{array}{*{20}{c}} {F\left( {{X_1}} \right)} \\ \vdots \\ {F\left( {{X_i}} \right)} \\ \vdots \\ {F\left( {{X_N}} \right)} \end{array}} \right]_{N \times 1}},$$
(3)

where F is the objective function vector and \({F_i}\) is the objective function value of the i-th candidate solution.

Moving towards prey stage

At this stage, pelicans recognize the position of their prey and move towards them. The random distribution characteristics of prey in the search space enhance the global optimization ability of the algorithm. In each iteration, the mathematical model of the new position of the pelican is represented by Eq. (4).

$$x_{{i,j}}^{{{P_1}}}=\left\{ {\begin{array}{*{20}{l}} {{x_{i,j}}+\operatorname{rand} \cdot \left( {{p_j} - I \cdot {x_{i,j}}} \right),}&{{F_p}<{F_i};} \\ {{x_{i,j}}+\operatorname{rand} \cdot \left( {{x_{i,j}} - {p_j}} \right),}&{{\text{ else, }}} \end{array}} \right.$$
(4)

where \(x_{{i,j}}^{{{P_1}}}\) is the new state of the i-th pelican in the j-th dimension based on the stage of moving towards prey, I is a random number which is equal to 1 or 2, ,\({P_j}\) is the location of prey in the j-th dimension, and \({F_P}\) is its objective function value.

In POA, if the value of the objective function is better at that position, the pelican’s new position is accepted. In this type of update, it is called effective update, which can prevent the algorithm from moving to non-optimal areas. This process is modeled using Eq. (5).

$${X_i}=\left\{ {\begin{array}{*{20}{c}} {X_{i}^{{{P_1}}},\;\;\;{\kern 1pt} F_{i}^{{{P_1}}}<{F_i};} \\ {{X_i},\;\;\;{\kern 1pt} {\text{ else, }}} \end{array}} \right.$$
(5)

where \(X_{i}^{{{P_1}}}\) is the new position of the i-th pelican, and \(F_{i}^{{{P_1}}}\) is its objective function value based on the stage of moving towards prey.

Water spreading stage

At this stage, the pelican reaches the surface of the water, flaps its wings, forces the fish towards shallow waters, and captures it in its own throat to store it before continuing to hunt for the next prey. The behavior of pelicans during hunting can be mathematically modeled using Eq. (6).

$$x_{{i,j}}^{{{P_2}}}={x_{i,j}}+R \cdot \left( {1 - \frac{t}{T}} \right) \cdot (2 \cdot \operatorname{rand} - 1) \cdot {x_{i,j}},$$
(6)

where \(x_{{i,j}}^{{{P_2}}}\) is the new position of the i-th pelican in the j-th dimension based on this stage, R is a constant, which is equal to 0.2, t is the iteration counter, and T is the the maximum number of iterations. The coefficient “\(R \cdot (1 - \frac{t}{T})\)” represents the radius of the neighborhood of the population members to search locally near each member to converge to a better solution. This coefficient is effective on the POA exploitation power to get closer to the optimal global solution.

At this phase, effective updating has also been used to accept or reject the new pelican position, which is modeled in Eq. (7).

$${X_i}=\left\{ {\begin{array}{*{20}{c}} {X_{i}^{{{P_2}}},\;\;\;{\kern 1pt} F_{i}^{{{P_2}}}<{F_i}} \\ {{X_i},\;\;\;{\kern 1pt} {\text{ else }},} \end{array}} \right.$$
(7)

where \(X_{i}^{{{P_2}}}\) is the new position of the i-th pelican and \(F_{i}^{{{P_2}}}\) is its objective function value based on this phase.

Although POA has certain advantages in solving specific problems, its shortcomings of lacking population diversity and the imbalance between exploration and development are equally evident. Therefore, we combine Logistic chaotic mapping with triangular walk strategy to effectively solve this problem. Next, we will provide a detailed introduction to these two improvement strategies.

Initialization of logistic chaotic mapping

The combination of chaotic mapping and POA to improve the performance of POA is no longer an exception. For example, in reference35, the author used six different chaotic maps as chaotic vectors to initialize the position of pelicans, greatly improved the convergence speed of POA; In reference36, the author used fractional-order chaotic to initialize the population members of the POA instead of random initialization, and enhanced the diversity of the population and accelerated the speed of finding the optimal solution; In reference37, the author introduced ten different chaotic mappings and introduced chaotic interference factors to act on the exploration and development stages of POA, thereby improving the search accuracy of POA. The method of combining chaotic mapping with POA in this manuscript is similar to the above literature, which applies logistic chaotic mapping to the initialization stage of POA to enhance the randomness of the POA initialization process.

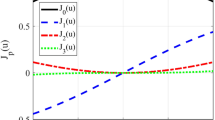
Logistic chaotic mapping is capable of generating sequences with similar random properties. Within the appropriate parameter range, the generated sequence has traversal within a certain interval, meaning that the values in the sequence will be widely distributed within the defined interval, as if they were randomly generated. In optimization algorithms, logistic chaotic maps can be used to initialize populations or update search directions. The randomness of chaotic sequences helps to diversify the search space, enabling algorithms to escape from local optima.

At the same time, the generated chaotic sequence can cover a wide range of values, which enables more comprehensive exploration of possible solutions in algorithms with larger search spaces. Compared with ordinary random search, chaotic search utilizes the inherent laws of chaotic sequences, which not only ensures the search range, but also enables more orderly search through its deterministic side, thereby improving search efficiency to a certain extent. In this manuscript, logistic chaotic mapping is combined with the initialization process of POA to enhance the randomness of the POA initialization process. Its mathematical expression can be represented by Eq. (8).

$${X_{n+1}}=r{X_n}(1 - {X_n}),$$
(8)

where \({X_{n+1}}\) is the value of the (n + 1)-th iteration, \({X_n}\) represents the value of the n-th iteration, r is a control parameter, and the value range is usually \(0<r \leqslant 4\). The value range of \({X_n}\) is \(0 \leqslant {X_n} \leqslant 1\).

The mapping distribution generated by Logistic chaotic mapping is shown in the Fig. 2.

Fig. 2
figure 2

Logistic chaotic mapping distribution map.

Full size image

Triangle walk strategy

Triangle walk strategy is used to increase the search diversity of algorithms and avoid them falling into local optima too early. It uses three different search agents to construct a triangle, calculates the centroid of the triangle through a triangle walk optimization function, and explores based on the centroid value during algorithm iteration, making the algorithm search a wider range in the search space and increasing the possibility of finding the global optimal solution. As shown in Fig. 3, it is its logical thinking diagram.

Fig. 3
figure 3

Logical thinking diagram of triangle walking strategy.

Full size image

Meanwhile, when combined with other stages such as prey movement and water diffusion in the Pelican Optimization Algorithm, it can further enhance the exploration and development capabilities of the Pelican Optimization Algorithm. Its mathematical expression can be represented by Eq. (9).

$$C=\frac{1}{3}({X_i}+{X_z}+{X_k}),i=1,2 \cdots ,W,z=\bmod (i+1,W)+1,k=\bmod (i+2,W)+1$$
(9)

where C represents the centroid of the triangle, W represents the number of walks, \({X_i}\)represents the optimal solution for the\(i - th\)walk, and \({X_z}\) and \({X_k}\) represent candidate solutions generated around \({X_i}\).

After knowing the center of gravity of the triangle, it is necessary to update the current search position, and the updated mathematical expression is represented by Eq. (10).

$$X_{i}^{W}=C+{R_m}(C - {X_i}),$$
(10)

where \(X_{i}^{W}\)represents the updated position, \({R_m}\) represents the random value of [1, m], and m represents the number of variables in the current algorithm.

Improved CTPOA flowchart

Due to the lack of population diversity and the imbalance between exploration and development in the POA, in order to improve these issues and enhance the performance of the algorithm, we added chaotic mapping during the initialization process to solve the problem of insufficient population diversity. In addition, after the water spreading stage, we added a triangle walking strategy to improve the imbalance between exploration and development, and named the improved POA the Chaotic Triangular Pelican Optimization Algorithm or CTPOA. The flowchart of the proposed CTPOA is shown in Fig. 4.

Fig. 4
figure 4

The flow chart of CTPOA.

Full size image

Benchmark function testing

Introduction to test functions

In order to test the performance of the CTPOA, we selected 8 test functions from the classic 2005 test functions for performance testing. Among them, F1-F3 are unimodal functions used to test the convergence ability of the algorithm, F4-F9 are simple multimodal functions used to test the algorithm’s ability to break out of local optima, and F11 is a mixed function used to increase the difficulty of algorithm optimization. The specific function expression is shown in Table 1.

Table 1 Test function information.
Full size table

Test function results of CTPOA and other algorithms

In this section, we compared the improved CTPOA with six other algorithms, namely Butterfly optimization algorithm (BOA)38, Particle swarm optimization (PSO), Grey wolf optimizer (GWO)39, Dung beetle optimizer (DBO)40, Sparrow search algorithm (SSA)41, and the original Pelican optimization algorithm (POA). The optimal, worst, mean, and standard deviation results of these 7 optimization algorithms, including CTPOA, are shown in Table 2. The bolded parts represent CTPOA. The number of function evaluations curve graph and matching 3D stereo image of the comparison are shown in Fig. 5; For this result, we set the number function evaluations (NFEs) is 15,000, uniform population size to 30, maximum iteration count to 500, run 30 times, and obtained it using a 13th generation Intel (R) Core (TM) i7-1360P 2.20 GHz computer configuration in MATLAB R2022a on Windows 11.

Table 2 Optimization results of test functions for 7 algorithms.
Full size table
Fig. 5
figure 5figure 5figure 5

The 3D three-dimensional images (left) and comparison plots of number of function evaluations curves (right).

Full size image

Based on the data in Table 2 and the number of function evaluations curve results in Fig. 5, it can be analyzed that the CTPOA has better convergence and stronger optimization ability in multiple test functions such as F1-F4 and F7. As is well known, the mean and standard deviation can characterize the stability of an algorithm. In the results of Table 2, the mean and standard deviation of CTPOA are smaller, indicating that CTPOA has better stability. Of course, in other test functions, our convergence and optimization abilities can also be comparable to other algorithms.

Pattern synthesis of linear antenna array

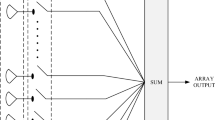
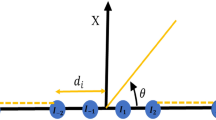
The geometric diagram of the linear array antenna is shown in Fig. 6, As shown in the figure, the linear antenna array consists of 2 N array elements arranged symmetrically on a horizontal line. If the array elements are arranged at an equal distance, it is called an equidistant symmetric array. If the distance between the array elements is not equal, it is called a non-equidistant symmetric array42.

Fig. 6
figure 6

Geometric illustration of a linear antenna array.

Full size image

Due to its left-right symmetry, its array factor (AF) in the azimuth plane can be represented by Eq. (11)43.

$$AF(\theta )=2\sum\limits_{{n=1}}^{N} {{I_n}\cos (k{x_n}\cos (\theta )+{\varphi _n})} ,$$
(11)

where \({I_n}\) and \({\varphi _n}\) are the excitation amplitude and phase in the array, and \({x_n}\) denotes the position of the array element, k is the wave number and is given by \(2\pi /\lambda\) and \(\theta\) is the azimuth angle.

To verify the performance of CTPOA, we conducted two types of simulation experiments in a linear array antenna. One type is in an equidistant linear array, assuming the excitation phase \({\varphi _n}\)= 0, optimizing the excitation amplitude of each element is optimized ; Another type is in non equidistant linear arrays, assuming the excitation phase \({\varphi _n}\)= 0 and the excitation amplitude \({I_n}\) =1, the spacing between array elements is optimized.

Antenna current optimization

In this section, we set up two models, a 20 element array and a 32 element array, to optimize the current amplitude and verify the performance of CTPOA. To reduce the complexity of the problem, we set \({\varphi _n}\)= 0. According to Eq. (11), the expression for the array factor can be expressed as Eq. (12).

$$AF(\theta )=2\sum\limits_{{n=1}}^{N} {{I_n}\cos (k{x_n}\cos (\theta ))}$$
(12)

In an equally spaced antenna array, the positions of antenna elements are fixed as \({x_n}=nd\), where d is equal to \(\lambda /2\). Moreover, we have also set a suitable fitness function to reduce the peak SLL, as shown in Eq. (13).

$$Fitness=\hbox{min} (\hbox{max} (20\log |AF(\theta )|))$$
(13)

Among them, \(\hbox{max} (20\log |AF(\theta )|)\) gives the maximum SLL (peak SLL). \(AF(\theta )\) is the array factor given by Eq. (12). In addition, we set the population size to 30 and the maximum number of iterations to 1000.

20 element array optimized current

We consider a 2 N = 20 linear array to achieve the lowest possible SLL in regions θ = [0 °,82 °] and θ = [98 °,180 °]. Of course, we also used other algorithms to optimize the model, such as traditional methods, DBO, MVO algorithm44, and the original POA, and compared their results with CTPOA. Table 3 shows the peak SLL and corresponding current amplitudes of the uniform array, DBO, MVO algorithm, POA, and CTPOA, respectively. By optimizing the current amplitudes in the table, the array pattern of the antenna model can be plotted as shown in Fig. 7. Based on the size of the optimized peak SLL, it can be intuitively compared which algorithm has stronger performance in reducing antenna sidelobes. More precisely, the peak SLL of CTPOA in this model is −32.92 dB, which is 19.74 dB lower than the uniform array, 5.78 dB lower than the DBO, 1.43 dB lower than the MVO algorithm, and 0.32 dB lower than the POA. Based on the data results, it can be concluded that the CTPOA has stronger optimization ability in this model.

Table 3 Optimized current amplitudes for peak SLL minimization: 2 N = 20 elements.
Full size table
Fig. 7
figure 7

Array directional diagram for optimizing current amplitude in a 20 element array.

Full size image

32 element array optimized current

In this example, an array with 2 N = 32 elements is optimized to achieve minimum SLL, andits sidelobe range is in the region of θ = [0 °,85 °] and θ = [95 °,180 °]. Similarly, we still used different methods to optimize the peak SLL and compared the results with them. Table 4 shows the peak SLL and corresponding current amplitudes for uniform array, ALO algorithm45, MVO algorithm, POA, and CTPOA, respectively. According to the current amplitude in Table 4, the array pattern of the antenna model is shown in Fig. 8. Specifically, the peak SLL optimized by CTPOA is -36.98dB, which is 23.50 dB lower than the uniform array, 26.63 dB lower than the ALO algorithm, 2.35 dB lower than the MVO algorithm, and 0.73 dB lower than POA. It can be seen that CTPOA also has superior performance in optimizing the model.

Table 4 Optimized current amplitudes for peak SLL minimization: 2 N = 32 elements.
Full size table
Fig. 8
figure 8

Array directional diagram for optimizing current amplitude in a 32 element array.

Full size image

Antenna position optimization

In this section, while reducing peak SLL, we need to achieve deep nulls in the specified directions to counteract the impact of strong interference on the performance of the array; The fitness function corresponding to it is given by Eq. (14).

$$Fitnsss={\sum\limits_{i} {\frac{1}{{\Delta {\theta _i}}}{{\int_{{{\theta _{li}}}}^{{{\theta _{ui}}}} {|AF(\theta )|} }^2}d\theta +\sum\limits_{k} {|AF({\theta _k})|} } ^2}$$
(14)

Where \({\theta _{li}}\) and \({\theta _{ui}}\) are the spatial regions in which SLL is suppressed and \(\Delta {\theta _i}={\theta _{ui}} - {\theta _{li}}\). The null direction is given by \({\theta _k}\). Equation (14) introduces a fitness function consisting of two terms. The first term focuses on restraining the SLL while the second term considers the positioning of nulls in the specified directions. \(AF(\theta )\) is the array factor given by Eq. (12).

This section also sets up two examples, a 20 element array and a 32 element array, but the optimization in this section focuses on the element positions to achieve the goal of minimizing peak values and forming deep nulls. Similarly, we set the overall size to 30 and the maximum number of iterations to 1000.

Minimize peak SLL and form nulls for a 20 element array

In this example, an array of 2 N = 20 elements is optimized to minimize peak SLL and nulls, and set its sidelobe range within the range of θ=[0 °, 82 °] and θ=[98 °, 180 °], as well as the placement of nulls at θ = 64 °,76 °,104 ° ,and 116 °, and record its first null beam width (FNBW). Table 5 shows the optimized array element positions, peak SLL, and FNBW for DA (Dragonfly Algorithm)46, black widow optimization algorithm (BWOA)47, MVO algorithm, POA, and CTPOA. Table 6 shows the values corresponding to different algorithms’ nulls. The array orientation diagrams optimized by different algorithms are shown in Fig. 9.

Table 5 Optimized element positions, peak SLL, and FNBW of a 20 element array.
Full size table
Table 6 Null depth: 2 N = 20 elements.
Full size table

From the data results in Table 5, the results show that the peak SLL of the CTPOA is -23.55 dB, and the FNBW is 17.4 °; Compared with the DA (Dragonfly Algorithm), the FNBW is not widened, but the peak SLL is reduced by 0.84 dB; Compared with the BWOA, although FNBW has widened 3°, the peak SLL has decreased by 8.04 dB; Compared to the MVO algorithm, the FNBW narrowed by 0.8 ° and the peak SLL decreased by 1.49 dB; Compared to the POA, the FNBW narrowed by 0.8 ° and the peak SLL decreased by 0.2 dB. From the results in Table 6, it can be seen that at the set nulls, the values of DA are − 63.88 dB and − 78.48 dB, BWOA are − 66.33 dB and − 63.57 dB, MVO algorithm are − 70.00 dB and − 78.11 dB, POA are − 86.33 dB and − 82.62 dB, and CTPOA are − 89.10 dB and − 86.61dB. Compared with the other three algorithms, the results of CTPOA are superior to them. From here we see that the CTPOA has strong performance in antenna optimization.

Fig. 9
figure 9

Array directional diagram for optimizing element positions in a 20 element array.

Full size image

Minimize peak SLL and form nulls for a 32 element array

In this section, we propose an array of 2 N = 32 elements to minimize SLL and nulls, and set its sidelobe range within the range of θ=[0 °, 87 °] and θ=[93 °, 180 °], as well as the placement of nulls at θ = 81 °and 99 °, and record its half power beam width (HPBW). Table 7 shows the peak SLL values of RRA (Runner-root algorithm)41, POA, and CTPOA, corresponding to the values of nulls and half power beam width, respectively. From the results in Table 6, the data results show that the peak SLL of CTPOA is -20.10 dB, the nulls value is -125.39 dB, and the HPBW is 3.7 °. Compared with RRA, the peak SLL is reduced by 1.5 dB, the nulls value is reduced by 40 dB, and the HPBW is narrowed by 0.1 °. Compared with POA without improvement, although their HPBW is the same, the peak SLL of CTPOA is reduced by 0.36 dB, and the nulls value is reduced by 18.47 dB. The optimized array element positions are shown in Table 8. The optimized array element orientation diagram is shown in Fig. 10.

Table 7 Peak SLL, null depth, and HPBW optimized for a 32 element array.
Full size table
Table 8 Optimized array element positions: 2 N = 32 elements.
Full size table
Fig. 10
figure 10

Array directional diagram for optimizing element positions in a 32 element array.

Full size image

Conclusions

In this manuscript, the basic principles and mathematical models of POA are briefly introduced, and two modification strategies, namely Logistic chaotic mapping initialization and triangle walk optimization, are proposed on the original POA. We named the improved POA as CTPOA, and also conducted performance tests on CTPOA using the classic test function 2005. We compared CTPOA with five other well-known algorithms and the original POA, and the results showed that CTPOA has faster optimization speed and stronger optimization ability. In addition, we also apply the CTPOA to optimize array antennas, which is also the first time CTPOA has been applied to array antenna optimization. In order to obtain the lowest sidelobe, deep zero point, and array pattern in the specified direction, we designed four simulation experiments using CTPOA, from the aspects of optimizing current amplitude and element spacing. From the results of the simulation experiment, it can be seen that in terms of optimizing the current amplitude, the peak SLL of CTPOA is lower, which is superior to several other compared algorithms; In terms of optimizing the spacing between array elements, compared with other algorithms, CTPOA has lower values for both peak SLL and deep zero, which highlights its superior performance in optimizing array antennas.