Multi objective elk herd optimization for efficient structural design

Abstract

This research presents an advancement of the Elk Herd Optimization targeting specific real-world multi-objective optimization problems, this algorithm is stated as the multi-objective Elk Herd Optimization (MOEHO). MOEHO exploits reproductive behaviour among elk herds for balancing exploration and exploitation within the optimization procedure toward diversification and convergence. The algorithm performed better over the set of small-to-medium scale structural design problems thus is widely applicable in engineering design. Further, when compared with eight benchmark truss structures against five well-established algorithms the MOEHO has outperformed them in the perspective of performance parameters like Spacing (SP), Hypervolume (HV) and Inverted Generational Distance (IGD). More concrete statistical analysis through Friedman rank test also ascertains the robustness and efficiency of the algorithm, especially at high complexities in optimization. The research attracts attention to the ability of such an algorithm which maintains a balance between the exploration and exploitation. Computational efficiency of MOEHO and qualitatively diversifying solutions along Pareto front, makes it especially applicable in complex engineering applications. Further research into extension of MOEHO with applicability on more dimensional problems, applied even in energy systems optimization.

Introduction

Optimization constitutes the core function in handling complex problems of the real-world problems encountered in different fields like engineering, manufacturing, logistics, and resource management. Multi-objective optimization is much more important because it provides the capabilities to optimize, not just one but many conflicting objectives simultaneously.^1,2. Objectives often have conflict with each other, and therefore a solution must be found that satisfies the objectives such that different constraints are satisfied. In practice, it usually yields a set of solutions known as the Pareto-optimal front, wherein no single solution strictly dominates all the others but represents a compromise that is accustomed by special preference^3,4. The tendency for increasing complexity attributed to engineering and computational challenges in modern industries has necessitated the establishment of robust optimization techniques. In this regard, conventional optimization methods always fail in dealing with nonlinear constraints, large search spaces, and complex dynamics of a problem, strictly limiting their capability to find optimal solutions. Under such challenges, a paradigm shift has been realized toward metaheuristic algorithms, which have gained immense popularity over the last two decades.^5,6. In contrast to traditional methods, metaheuristics do not make use of gradient information and thus can explore at a much larger extent the solution spaces and avoid better local optima pitfalls. This feature renders metaheuristic algorithms especially appealing when dealing with multiobjective optimization problems (MOPs), which involve optimizing conflicting objectives simultaneously⁷.

In principle, metaheuristic algorithms have an intrinsic difference: there is an iterative approach that modifies decision variables towards identifying optimal solutions. The two fundamental elements of such algorithms are exploration and exploitation. Exploration should focus on new regions within the search space; thus, it must have a global view and avoid getting trapped locally. However, the exploitation improves solutions in promising parts of the search space. It emphasizes precision and accuracy. These two phases must be well-balanced for metaheuristic optimization strategies to work.⁸. Over time, metaheuristics have developed into different types, each influenced by different natural events.

A significant group of these, called nature-inspired algorithms, are based on biological, physical, and ecological processes. For instance, Genetic Algorithms (GAs) use the idea of Darwin’s evolution to create groups of solutions by using methods like combining, changing, and choosing the best solutions. Some newer algorithms that are based on biological traits include differential evolution (DE)⁹, genetic programming (GP)¹⁰, and Spherical evolution algorithms¹¹, Salp Swarm Algorithm (SSA)¹², Monarch Butterfly Optimization (MBO)¹³, Tunicate Search Algorithm (TSA)¹⁴, Optimal Foraging Algorithm (OFA)¹⁵ , Wild Horse Optimizer (WHO)¹⁶ , etc.

Another category includes physics-inspired algorithms, which leverage principles from physical laws and processes¹⁷. Examples include Simulated Annealing (SA)¹⁸ , inspired by the annealing process in metallurgy, and Fick’s Law Algorithm (FLA)¹⁹, which models diffusion processes. Few more instances of physics motivated algorithms may be such as Water Cycle Algorithm (WCA)²⁰, Weighted Mean of Vectors (INFO)²⁰ and special relativity search (SRS) algorithm²¹. Such propositions are concerned more with the abstraction and provide teachings concerning the optimization of constraints’ performance. Some metaheuristic methods have been investigated for structural optimization, such as the Starfish Optimization Algorithm (SFOA) and Multi-objective SHADE with Manta Ray Foraging Optimizer (MOSHADE-MRFO)²². SFOA proved to be competitively effective in global optimization with a balance of exploration and exploitation. MOSHADE-MRFO has also been used in structural design tasks with effective convergence and diversity preservation²³.

Communal animal behaviour has been a major driving force for the design of optimization algorithms. Swarm intelligence-based algorithms imitated behaviours of hunting, food foraging or migration. The widely accepted algorithms in this category include: Chameleon Swarm Algorithm (CSA)²⁴Nutcracker Optimization Algorithm (NOA)²⁵, White Shark Optimization Algorithm (WSO)²⁶, Geyser Heuristic Algorithm²⁷, Zebra Optimization Algorithm²⁸, Egret Swarm Optimization Algorithm²⁹, Waterwheel Plant Algorithm³⁰, Mantis Search Algorithm³¹, Chameleon Swarm Algorithm (CSA)²⁴ , Crayfish Optimization Algorithm³², Electric Eel Optimizer³³ , Orca Predation Algorithm (OPA)³⁴, Prairie Dog Optimizer algorithm³⁵ and so on. These algorithms use how animals act to create new ways of searching for the best solutions in complex problems. The main focus of this research is on three methods: (1) making existing algorithms better^36,37, 2) creation of the most modern algorithms and 3) development of hybrid algorithms³⁸. Recent advances in multi-objective optimization algorithms includes “Multi-objective heat transfer optimization (MOTEO)³⁹, Two-archive multi-objective multi-universe optimization (MOMVO2arc)⁴⁰, multi-objective hippo optimization (MOHO )⁴¹, multi-objective geometric mean Optimizer (MOGMO)⁴² , Multi-objective Resistor-Capacitance Optimization (MORCO)⁴³, Multi-objective Artificial Hummingbird Algorithm (MOAHA)⁴⁴, Multi-objective Water Strider (MOWSO)⁴⁵, Multi-objective Liver Cancer Algorithm (MOLCA)⁴⁶, Multi-objective Snow Ablation Optimization Algorithm (MOSAO)⁴⁷ and so on. These algorithms elucidate how to integrate advanced methods in engineering applications to achieve a balance between objectives. Hybrid algorithms use a weighted average to combine the advantages of multiple optimization methods⁴⁸. By using the weighted average of the solutions produced by different methods, these algorithms increase the ability to efficiently explore the search space, thereby reducing the probability of entering the local optimal region⁴⁹. This methodology increases the overall power and flexibility of the algorithm, resulting in optimal solutions for various problems.^50,51

The "no free lunch" optimization theory⁵² shows that a single optimization algorithm is not applicable for all types of problems. Metaheuristics are good for certain problem domains, but not good at providing optimal solutions for other problem domains. This inconsistency often stems from a failure to strike the perfect balance between research and development. As a result, these can cause the algorithm to search well or fail at local optima. Thus, it is required to build novel algorithms in the interest of distinct optimization test cases⁵³.

This research presents an extension of the recently developed Elk Herd algorithm, called multiobjective Elk herd optimization algorithm (MOEHO), useful for solving multi-objective optimization problems of engineering design. The EHO algorithm is a relatively recent addition to the family of nature-inspired metaheuristics. It models the social and reproductive behavior of elk herds, focusing on the seasonal dynamics of rutting and calving. During the rutting season, dominant male elks or bulls compete for control over groups of females known as harems. This naturally leads to a hierarchy within the herd, and each harem forms a subgroup of solutions. Introducing new solutions through calving is similar to the illusion of genetic diversity in reproduction. Finally, the selection process provides a solid foundation for the best solutions, so the algorithm moves progressively toward optimality. MOO is optimizing two or more conflicting objectives. For instance, reducing material cost in engineering design usually conflicts with increasing structural strength. Logistics often increases transportation cost to reduce the delivery time. The central idea in MOPs is called Pareto optimality^51,54,55.

A solution is Pareto-optimal if no other solution is better for any one objective without deteriorating another. The set of Pareto-optimal solutions forms the Pareto front, which allows the researcher to select a preferred solution from a range of trade-offs. Generating an appropriately distributed and accurate Pareto front is particularly difficult for high-dimensional, constrained, or multi-modal problem spaces. Key issues in multi-objective optimization are: Diversity Maintenance: the true Pareto front is approximated, and the possibility of being trapped in a local optimum. Handling Constraints: how to handle complex constraints that can reduce the size of the feasible region in the search space. Balancing Exploration and Exploitation: how to make sure an algorithm properly explores the search space and refines promising solutions. This paper introduces the elk herd optimization MOEHO, which is the advanced version of the EHO framework, and it aims at improving multiple objectives simultaneously. This makes MOEHO a powerful and efficient technique for solving complicated optimization problems with tools adapted to multiple objectives. Some of the key characteristics of MOEHO include:

1. Pareto-Dominance Ranking: Solutions are ranked based on the degree to which they are better than others, thus establishing a clear and accurate Pareto front.

2. Crowding Distance Approach: To promote diversity of the solutions, MOEHO computes crowding distances and then concentrates on the clean portions of the Pareto front.

3. Elite Retention: There is retention of elite solutions for several generations to guarantee progressive enhancement to the Pareto front.

4. Adaptive Parameter Settings: Parameters for searching and utilizing resources are modified in an adaptive manner with a view of maintaining a proper equilibrium between them for the whole period of optimization.

The mathematical model of elk herd optimization

The mathematical model of the optimiser elk herd is included within the optimisation framework. Before, elk had been divided into families according to the number of bulls in that family. Through the rutting season, the powerful male elk leads each family, and strength determines how many cows and harems to take. ⁵⁶. The strength of bulls can be measured through their ability to overthrow dominance. During the calving season, each family normally produces an equal number of calves. All the families are then combined during the chosen season, and the best candidates are once again invited to the mating season. To ensure that the produced elk herd can adapt to varying environmental conditions, this process is repeated. Six consecutive steps are proposed in the mathematical model to connect the elk herd’s reproduction cycle with an optimisation framework. We will go over each of these processes in great detail. This is the flowchart shown in picture 1 and the pseudo code that goes with it in algorithm 2. Figure 1 Showcase the flowchart of the EHO algorithm.

Step 1: Set the initial value for the EHO parameter and define the optimization problem

Fig.1

Flow chart for EHO algorithm.

Two such ingredients are necessary to incorporate problem-specific knowledge into the EHO: a representation that makes the search space obvious and an objective function that measures the answer. Each decision variable in a continuous search space has a specific range of values for simple optimisation problems. The objective can be expresses as per Eq. (1)

$$\text{min}f\left(x\right) x \epsilon ({L}_{B , }{U}_{B})x=\left({x}_{1, }{x}_{2, }\dots . , {x}_{n}\right)$$

(1)

f (x) = objective function, ${x}_{i}$= individual characteristic of specific elk classified by i.

$f\left(x\right) x \epsilon ({L}_{Bi , }{U}_{Bi}$) ${L}_{Bi}$= Lower limit, and ${U}_{Bi}$= Upper limit for the characteristic ${x}_{i}$ .

Step 2: Generate the initial elk herd

Elk solutions, such as bulls and harems, make up the first generation of the elk herd (E).

The E is a matrix of size n × Elks presented in Eq. (2).

$$E=\left[\begin{array}{ccc}{x}_{1}^{1}& {x}_{2}^{1}& \begin{array}{ccc}.& .& \begin{array}{cc}.& {x}_{n}^{1}\end{array}\end{array}\\ .& .& \begin{array}{ccc}.& .& \begin{array}{cc}.& .\end{array}\end{array}\\ \begin{array}{c}.\\ .\\ {x}_{1}^{Elks}\end{array}& \begin{array}{c}.\\ .\\ {x}_{2}^{Elks}\end{array}& \begin{array}{ccc}\begin{array}{c}.\\ .\\ .\end{array}& \begin{array}{c}.\\ .\\ .\end{array}& \begin{array}{cc}\begin{array}{c}.\\ .\\ .\end{array}& \begin{array}{c}.\\ .\\ {x}_{n}^{Elks}\end{array}\end{array}\end{array}\end{array}\right]$$

(2)

The solution ${x}_{j}$ can calculated using Eq. (3)

$${x}_{i}^{j}= {L}_{Bi }+({U}_{Bi}-{L}_{Bi })\text{x U }(0, 1)$$

(3)

The elks in E are organized in rising sequence on the basis of their qualification values, such as $f({x}^{1}$) $\le$ $f({x}^{2}$) $\le \dots \le f({x}^{Elk})$.

Step 3: Rutting season

The EHO is modelled to generate families according to the bull rate (Br) during rutting season. First, the total number of families is determined as B = Br × Elk. The bulls are selected from E with respect to the fitness values. According to Eq. (4), the elks of group B with the maximum qualification appear at the beginning of E as bulls. It is for combat command contests whereby the toughest elks are accorded more harems upon evaluation.

$$B=\text{arg min}f({x}^{j})$$

(4)

Then the bulls in the B set start fighting among themselves to form families. The harems are then allocated to every bull in B through using the roulette-wheel assortment method, based on how these bulls’ fitness values fall compared to the total fitness values. In practical terms, the selection probability ${p}_{j}$ for every bull ${x}^{j}$ in B would be obtained as per Eq. (5)

$${p}_{j}= \frac{f({x}^{j})}{\sum_{k=1}^{B}f({x}^{k})}$$

(5)

The bulls will receive the harem according to the selection likelihood ${p}_{j}$ obtained from Algorithm 1. A vector H = (${h}_{1,}{h}_{2, \dots }. {h}_{k}$), is utilized in the algorithm. The harems are denoted by k = Elk − B, wherein each is assigned by the bull catalogue that is recognized through roulette-wheel selection. For instance, if there are ten elk in the herd (Elk = 10) and the bull rate is 30%, B = 3 is showing the no. of families. The B = (${x}^{1},{x}^{2}.{x}^{3}$). It is possible to point the remaining elks (i.e., (${x}^{4}$,…,${x}^{10}$)) as harems, and then distribute them according to the roulette wheel selection.

Step 4: Calving Season

During the season when calf is born, each family’s calf is generated based on the qualities primarily occupied from their mother harem ${x}_{i}^{j}$ (t + 1)) and father bull ( ${x}^{hj}$). The calf is imitated as indicated by Eq. (6) if its index $i$ is the same as that of its bull father in the family ( ${x}_{i}$(t + 1)).

$${x}_{i}^{j}(\text{t }+ 1) ={x}_{i}^{j}(\text{t}) + \alpha { (x}_{i}^{k}(\text{t})-{x}_{i}^{j}(\text{t}))$$

(6)

In the herd ${x}^{k}(t)$, where k ∈ (1, 2, …, Elk), the rate of the hereditary qualities from the arbitrarily chosen elk is determined by α, which is a arbitrary value in the interval [0, 1]. It is worth noting that a large α increases the chance that random elements would share the new calf; thus, it enhances diversification. If the new index of the calf is equal to that of its mother, then it ${x}_{i}(t + 1)$ acquired the traits of the father bull ${x}^{hj}$ and mother harem ${x}^{j}$, respectively, as in Eq. (7).

$${x}_{i}^{j}(\text{t}+1)={x}_{i}^{j} (\text{t})+ \beta \cdot { (x}_{i}^{hj} (\text{t}) - {x}_{i}^{j} (\text{t}))+ \gamma \cdot { (x}_{i}^{r} (\text{t}) - {x}_{i}^{j} (\text{t}))$$

(7)

where the characteristic $i$ of the calf j at iteration t + 1 is represented by ${x}_{i}^{j}$ (t + 1) and will be placed in E’. r is the index of a randomly chosen bull from the present set of bulls, such that r ∈ B and ${h}_{j}$ denotes the bull for the harem j. In the wild, if the mother harem bull does not guard it well enough, it occasionally mates with other bulls. The portion of the characteristics hereditary received from formerly created calves are arbitrarily obtained by the arbitrary numbers γ and $\beta$, which fall between 0 and 2.

Equation 6 indicates that the coefficients β and γ are important variables in the suggested EHO because of their similarity to the “social” and “cognitive” models in the PSO. It should be highlighted that the utilization of temporary arbitrary values of β and γ in the range [0, 2] as a substitute of a predefined value would improve performance in some optimization cases. This can be attributed to the fact that random values for β and γ within the allowed range might demonstrate potential to obtain an acceptable degree of EHO performance.

Step 5: Selection time

The E’ that held the solutions of the calves and the E that had the solutions of the bulls and harem are united into a one matrix called ${\text{E}}_{temp}$. Based on their suitability value, the elks in the ${\text{E}}_{temp}$ will be sorted in rising sequence. In order to replace the elks in E, the better performing elks of ${\text{E}}_{temp}$ will be kept for the next generation, so that ${\text{E}}^{j}$= ${E}_{j}^{temp}$ j = (1…, Elk).

Step 6: Termination criteria

Steps 3, 4, and 5 are repeated till the stopping requirement is satisfied. Typically, the maximum number of iterations is used as a condition for termination; sometimes, this is optimality in ideal solutions reach, then computing time or the number of ideal iterations should not exceed that number.

Algorithm 1

:

Algorithm 2

The pseudo-code of EHO.

Multi-objective elk herd optimization algorithm

MOEHO algorithm begins by generating a random population. Let t represent the current generation.${a}_{i}^{t}$ and ${a}_{i}^{t+1}$ denoting the $i$-th individual in generation $t$ and $\left(t+1\right)$ respectively. Similarly, ${u}_{i}^{t+1}$ represents an individual in next generation, derived using EHO algorithm from parent population ${P}_{t}$. The fitness value of ${u}_{i}^{t+1}$ is given by ${f}_{i}^{t+1}$ and the set of all such individual is dented by ${U}^{t+1}$. The value of ${x}_{i}^{t+1}$ is computed based on ${u}_{i}^{t+1}$ incorporating the information feedback mechanism as defined in Eq. (8)

$${{x}_{i}^{t+1}={\partial }_{1}{u}_{i}^{t+1}+{\partial }_{2}{s}_{k}^{t};\text{ where }{\partial }_{1}=\frac{{f}_{k}^{t}}{{f}_{i}^{t+1}+{f}_{k}^{t}}, {\partial }_{2}=\frac{{f}_{i}^{t+1}}{{f}_{i}^{t+1}+{f}_{k}^{t}}}_{ },\text{ ensuring }{\partial }_{1}+{\partial }_{2}=1$$

(8)

here, ${x}_{k}^{t}$ represents the selected $k-th$ individual from generation t, with fitness value of ${f}_{k}^{t}.\text{ The coefficients}{\partial }_{1}$ and ${\partial }_{2}$ acts as weight factors. The offspring population, denoted as ${Q}_{t}$ consists of individuals ${a}_{i}^{t+1}.$ The combined population ${R}_{t}={P}_{t}\cup {Q}_{t}$ is then categorized into multiple non-dominated levels $\left({F}_{1},{F}_{2},\dots ,{F}_{l}\dots ,{F}_{w}\right).$ Starting from ${F}_{1}$, individuals level 1 to $l$ are included in ${S}_{t}={\bigcup }_{i=1}^{l} {F}_{i}$ while any remaining individuals in ${R}_{t}$ are discarded. If $\left|{S}_{t}\right|=N$ no further actions are needed, and the next generation proceeds directly with ${P}_{t+1}={S}_{t}$. Else, the individuals in $\frac{{S}_{t}}{{F}_{l}}$ are added in ${P}_{t+1}$ while the remaining $N-{\sum }_{i=0}^{l-1} \left|{F}_{i}\right|$ solutions are chosen from ${F}_{l}$ using the Crowding Distance (CD) mechanism. Solutions with larger crowding distance have a higher probability being selected. If the termination condition is not met, the process iterates with $t=t+1$ generating a new population ${Q}_{t+1}$ using EHO algorithm. The MOEHO approach follows a structured selection strategy, leading to a computational complexity of $O\left({N}^{2}M\right)$ for $M$-Objective optimization problem.

MOEHO begins with the first stage where there is a population of elk solutions that is generated randomly and estimated by objective functions. A population is divided into dominant males and harems, with dominant males contributing to exploration and the harems helping with local improvement. The movement schemes are employing front male leaders to discover new spaces with the adaptable step size, employing females for positioning adjustments according to the optimum solutions in their subgroup, and calves inheriting characteristics from parents with subtle perturbations for diversity. Dynamic equilibrium between exploration and exploitation is established by means of an adaptable parameter update strategy. To maintain the quality of solutions, an elite selection strategy is employed to preserve the best non-dominated solutions across generations. The algorithm terminates when a target number of iterations is reached or convergence conditions are met.

The MOEHO algorithm improves the traditional EHO with the addition of an information feedback mechanism, which improves offspring generation through the use of adaptive weight factors ∂1 and ∂2 derived from fitness values. This adjustment makes the trade-off between exploration and exploitation more balanced, leading the search process more efficiently towards the Pareto front. Moreover, the orderly selection strategy, which uses the non-dominated sorting and crowding distance mechanisms, enhances diversity of the solution and convergence. Through adaptive regulation of the impact of previous generation selected individuals, MOEHO sustains a more dynamic population updating, hence maintaining its capability to solve complex multi-objective problems with a better computational efficiency of O(N²M).

Pseudo-code of MOEHO algorithm.

The flow chart of MOEHO algorithm is shown in Fig. 2.

Fig.2

Flowchart of MEHO algorithm.

The Multi-Objective Elk Herd Optimization (MOEHO) algorithm is an advanced nature-inspired metaheuristic algorithm designed to solve multi-objective optimization problems. The algorithm is based on the social and reproductive behavior of elk herds, which is modeled to balance exploration and exploitation in the optimization process. The procedure of MOEHO is divided into several key steps, each of which is described in detail below.

Initialization

The MOEHO algorithm begins with the initialization of the population. The initial population consists of a set of randomly generated solutions, each representing a potential solution to the optimization problem. The population size is denoted by $N$, and each solution is represented as a vector of decision variables ${x}_{i}$, where $i=\text{1,2},\dots ,N$. The decision variables are initialized within the specified lower and upper bounds $[{L}_{Bi},{U}_{Bi}]$ for each variable.

Fitness evaluation

Once the initial population is generated, the fitness of each solution is evaluated based on the objective functions of the optimization problem. For multi-objective optimization, the fitness evaluation involves calculating the values of multiple conflicting objectives. The fitness values are used to rank the solutions and determine their dominance relationships.

Rutting season (exploration phase)

The rutting season in MOEHO corresponds to the exploration phase of the optimization process. During this phase, the population is divided into families based on the bull rate ${B}_{r}$, which determines the number of dominant solutions (bulls) in the population. The bulls are selected based on their fitness values, with the fittest solutions being chosen as bulls. Each bull is then assigned a harem of solutions (cows) using a roulette-wheel selection mechanism, where the probability of selection is proportional to the fitness of the bulls. The exploration phase is crucial for maintaining diversity in the population. The bulls compete for dominance, and the harems are redistributed based on the fitness of the bulls. This competition ensures that the algorithm explores different regions of the search space, preventing premature convergence to local optima.

Calving season (exploitation phase)

The calving season represents the exploitation phase of the MOEHO algorithm. During this phase, new solutions (calves) are generated by combining the characteristics of the bulls and cows. The calves are created using a combination of genetic operators, including crossover and mutation. The crossover operator combines the traits of the bull and cow to produce a new solution, while the mutation operator introduces random variations to maintain diversity. The exploitation phase focuses on refining the solutions in promising regions of the search space. The new solutions are evaluated, and their fitness values are compared to those of the existing solutions. The best solutions are retained for the next generation, ensuring that the algorithm converges towards the Pareto-optimal front.

Selection and elitism

After the calving season, the population is updated by selecting the best solutions from the combined set of bulls, cows, and calves. The selection process is based on the Pareto dominance ranking and crowding distance. Solutions that are non-dominated and have a higher crowding distance are preferred, as they contribute to a well-distributed Pareto front. Elitism is also incorporated into the selection process to ensure that the best solutions from the current generation are carried over to the next generation. This helps in maintaining the quality of the solutions and accelerates the convergence of the algorithm.

Termination CSriteria

The MOEHO algorithm iterates through the rutting season, calving season, and selection process until a termination criterion is met. The termination criterion can be based on the maximum number of iterations, the quality of the solutions, or the computational time. Once the termination criterion is satisfied, the algorithm returns the set of non-dominated solutions, which form the Pareto-optimal front.

Information feedback mechanism (IFM)

The MOEHO algorithm incorporates an Information Feedback Mechanism (IFM) to enhance its performance. The IFM uses the fitness values of the solutions from the current and previous generations to guide the search process. The feedback mechanism adjusts the weights of the solutions based on their fitness values, ensuring that the algorithm explores the search space more effectively. The IFM is particularly useful in maintaining a balance between exploration and exploitation. By incorporating feedback from previous generations, the algorithm can adaptively adjust its search strategy, leading to faster convergence and better-quality solutions.

MOEHO represents an enhanced version of EHO which specifically targets engineering design problems with multiple optimization objectives. MOEHO implements structural changes that optimize its exploration–exploitation capabilities to achieve reliable performance in different optimization environments. Multiple improvements implemented in MOEHO consist of Information Feedback Mechanism (IFM) and adaptive parameters with Pareto-dominance ranking that result in enhanced capability for handling conflicting objectives while preserving diverse solutions on the Pareto front. The Information Feedback Mechanism represents a vital update in MOEHO that enhances solution quality through the utilization of previous generation data. Through this mechanism the algorithm maintains important insights discovered in prior generations to direct its search in future generations. The feedback system enables MOEHO to improve its search path automatically which prevents premature convergence to substandard solutions. MOEHO maintains exploration of new search regions while exploiting previously identified promising areas through its use of historical data.

MOEHO implements dynamic parameter adjustments which modify exploration and exploitation capabilities of the optimization algorithm during its execution. The parameters play an essential role in striking the right equilibrium between searching the entire space and optimizing promising areas. Through its adaptive mechanism MOEHO establishes the capability to search high-dimensional complex spaces without remaining in sub-optimal solutions. During calving season the algorithm adjusts β and γ coefficients adaptively to determine how much trait information parents will pass to their offspring solutions. Random coefficient values inside defined boundaries enable MOEHO to generate diverse offspring solutions. The random elements in the algorithm enable it to investigate various search areas without compromising solution quality.

MOEHO solves multi-objective optimization problems by applying Pareto-dominance ranking to determine the solution rankings through dominance relationship comparisons. The algorithm focuses on non-dominated solutions through this method which enables it to produce an approximation of the Pareto front. The crowding distance metric in MOEHO functions to maintain diverse solutions. The crowding distance calculation determines solution density on the Pareto front to guide exploration toward underpopulated areas while maintaining diverse solution distributions. MOEHO maintains an elite retention system that enables the algorithm to keep superior solutions from one generation to the next. The best-performing solutions remain in the optimization process through this strategy which prevents valuable information loss and speeds up the convergence to the Pareto front. MOEHO effectively supports multi-objective optimization through elite solution retention because it preserves both essential elements of convergence and diversity.

MOEHO receives substantial improvements in its performance for multi-objective optimization through the implemented modifications. The IFM enables the algorithm to use historical data for optimizing its search while adaptive parameter settings help it control its exploration and exploitation behavior. The Pareto-dominance ranking together with crowding distance mechanisms allow MOEHO to maintain a diverse collection of solutions that span the entire Pareto front. The combination of these improvements enables MOEHO to deliver superior performance than conventional optimization algorithms regarding solution speed and diversity as well as quality thus establishing itself as an effective tool for complex engineering design tasks.

The MOEHO mathematical model uses elk herd reproductive behavior to divide its process into six essential stages starting with initialization followed by rutting season then calving season then selection before termination. Dominant bulls create harems during rutting season to produce new solutions through the calving season. Selection mechanisms within the process maintain only superior solutions for the next generation and termination criteria establish the conclusion of optimization. The MOEHO optimization framework works with both continuous domains as well as discrete domains because it provides flexibility across multiple engineering applications. MOEHO functions as an advanced optimization tool for structural design and additional applications because it maintains adaptive exploration–exploitation balance and shows robustness in multi-objective optimization.

Formulating the truss design problem

Muti-objective truss design problem

MOO truss problem is a challenging task because of the conflicting objectives, complicated constraints, and discrete variables related to the cross-sectional regions. To minimize the total weight and compliance while satisfying the given stress limits, the main objective of this paper is to solve the multi-objective truss optimization problem⁴⁹. Since the goals are conflicting, they cannot be achieved simultaneously in a way that maximizes total value. Moreover, the nonlinear stress limitations also bound the range of design variables, making optimal design problems more complex. Instead of a unique optimal solution, the problem with multiobjective truss optimisation seeks for a pareto solution set; a set consisting of all viable alternatives that do not dominate another alternative. A multiple objective truss optimisation formulation is illustrated in the expression as follows:

$$\text{Find X}=\{{x}_{1, }{x}_{2, }{x}_{3, \dots .., }{x}_{m, }\}$$

(9)

$$\text{Min }{f}_{1}\left(x\right)= \sum_{i=1}^{m}{A}_{i}{\rho }_{i}{L}_{i} \text{and Min }{f}_{1}\left(x\right)=compliance= {u}^{T}F$$

(10)

Subject to constraints:

$$\left|{\sigma }_{i}\right|-{\sigma }_{max} \le 0\text{and }{A}_{i}^{min}\le {A}_{i}\le {A}_{i}^{max}$$

(11)

where ${A}_{i}$ = cross-sectional area for ${i}^{th}$ element, m = number of design variables,

${f}_{1}$= structural compliance; ${f}_{2}$= mass compliance, ${\rho }_{i}$= mass density and ${L}_{i}$ = length of the ${i}^{th}$ element, ${\sigma }_{i}$ = stress ${\sigma }_{max}$= the allowable stress, and ${A}_{i}^{min}$ = Lower bounds and ${A}_{i}^{max}$ = Upper of cross-sectional areas.

Formulation of different Truss structures

The design variables are considered discrete, reflecting the constraints often found in real-world applications for truss element sizing. Figs 3,4,5,6,7,8,9,10 illustrate the truss structures for each case.

Fig.3

10 bar Truss.

Fig.4

25 bar Truss.

Fig. 5

37 bar Truss.

Fig.6

60 bar Truss.

Fig. 7

72 bar tower truss.

Fig. 8

120 bar Truss Structure.

Fig. 9

200 bar Truss.

Fig.10

942 bar tower truss.

10-Bar planer truss

The 10-bar truss problem (Fig. 3) uses cross-sectional areas as design variables (${A}_{i}$ for i = 1, 2, …, 10). The size variables range between [1, 1.5, 2, …, 21] × 10⁻³ m². The loading condition involves downward forces of 1000 KN applied at nodes 2 and 4.

bar 3D truss

This truss, demonstrated in Fig. 4, also adheres to a stress constraint of stress. The loading condition is more complicated, requiring several forces at different nodes, but the design variables are similarly established. To manage the additional loading points while reducing weight and compliance, this structure needs to be optimized.

37-Bar planer truss

The material characteristics and stress limits of the 37-bar truss (Fig. 5) are identical to those of the 10-bar truss. It does, however, provide several loading scenarios with forces of 1000 KN. The range of the design variables doesn’t change.

60-Bar ring truss

The 60-bar ring truss (Fig. 6) follows the same material and stress constraints, with design variables within [1, 1.5, 2, …, 21] × 10 − 3 m². Multiple load cases are considered across different nodes, making optimization for both mass and stress distribution.

72-Bar tower 3-D truss

The 72-bar truss is shown in Fig. 7. The truss is subject to two loading conditions, requiring high optimization due to its complex force distribution.

bar truss

The 120-bar dome truss ground structures are indicated in Fig. 8.

200-Bar truss

The 200-bar truss (Fig. 9) adheres to the same stress, density, and Young’s modulus constraints as other trusses. This structure faces lateral and vertical loads at multiple nodes, increasing the complexity of the optimization problem.

942-Bar tower truss

The 942-bar tower truss, depicted in Fig. 10, is a highly complex structure subjected to various vertical and lateral loading conditions. Like the other trusses, it follows the same material constraints. The cross-sectional areas, denoted as Ai for i = 1, 2, …, 942, are chosen from a set of discrete values. The significant size and complexity of this structure require a broader range of cross-sectional areas to accommodate the substantial forces. The load cases are divided into sections, including vertical loadings of Pz =  − 100 KN and lateral loadings of Px =  ± 3 KN, which together ensure that the structure can withstand both horizontal and vertical forces.

Results and discussion

Convergence and diversity analysis of different truss structures

The comparative performance analysis of MOOA’s NSGA-II⁵⁷, MOEA/D⁵⁸, MOMPA⁵⁹, MOSAO⁶⁰, MOGNDO⁶¹, and MOEHO was completed on eight benchmark truss structures, with consideration given to two main objectives, weight minimization and minimization of compliance (structural performance maximization). The Pareto fronts obtained for all algorithms are illustrated in. Figs 11,12,13,14,15,16,17,18 Various performance metrics were employed to evaluate the efficiency of each algorithm in exploring and distributing solutions across the objective space, with hypervolume (HV) being one of the most significant indicators.

Fig.11

Optimum pareto fronts for 10-bar Truss using different algorithms.

Fig.12

Optimum pareto fronts for 25-bar Truss using different algorithms.

Fig.13

Optimum fronts for 37-bar Truss using different algorithms.

Fig.14

Optimum pareto fronts for 60-bar Truss using different algorithms.

Fig.15

Optimum pareto fronts for 72-bar Truss using different algorithms.

Fig.16

Optimum pareto fronts for 120-bar Truss using different algorithms.

Fig.17

Optimum pareto fronts for 200-bar Truss using different algorithms.

Fig.18

Optimum Pareto fronts for 942-bar Truss using different algorithms.

Table 1 summarizes the parameter settings used in the MO optimization algorithms covered in this work. The major parameters like population size, number of iterations, crossover and mutation strategies, and other algorithmic settings are provided to allow reproducibility. In particular, MOEHO uses an adaptive parameter updating mechanism with a male rate of 0.2 and elite preservation. In contrast, NSGA-II and MOEA/D use SBX crossover and DE crossover, respectively, with various mutation strategies. The application-specific mechanisms in MOSAO, MOMPA, and MOGNDO, e.g., snow ablation, Lévy flight mutation, and generalized normal distribution-based search, also reflect the richness of these methods. These parameter selections have an important bearing on the comparative performance evaluation of the algorithms for structural optimization problems.

Table 1 Parameter Settings of MO Optimization Algorithms Under Consideration.

MOEHO outperformed the other algorithms in terms of objective space exploration and achieved a closely packed Pareto solution set. This algorithm achieved higher values of hypervolume (HV) hence able to cover a wider portion of the objective space and produce better solutions. Thus, it can be concluded that MOEHO can produce a larger set of complete non dominated solutions than the other approaches. These results show that the design space in MOEHO is much more effectively searched and exploited than for any of the other algorithms tested. It does this while correctly approximating the True Pareto Front, and maintains the solutions well distributed across the entire design objective space. The ability of MOEHO to provide high HV confirms the correctness of the solutions it can provide. This is attributed to capability of MOEHO to appropriately balance convergence and diversity without compromising on either of them.

The diverse pareto fronts that MOEHO provides shows that the trade-offs between objectives, for instance between weight minimization and compliance minimization are well accomplished. One of the advantages is flexible properties that help to disperse the solutions. Often the non-dominated strategy of MOEHO is more accepted than other approaches like NSGA-II, MOEA/D, and MOMPA which have more limited and even dispersion when addressing multi-objective truss optimization.

Figures 11 through 18 depict the Pareto optimality achieved by several algorithms NSGA-II, MOEA/D, MOMPA, MOSAO, MOGNDO, and MOEHO across a variety of truss configurations. These range from relatively simple 10-bar and 25-bar structures to highly complex designs like 200-bar and 942-bar configurations. For simpler truss setups, the Pareto fronts generated by different algorithms were closely clustered, reflecting effective optimization with minimal trade-offs between conflicting objectives, such as minimizing weight and improving structural performance.

The Pareto solutions created by MOEHO for the 942-bar truss structure show minor differences from reference solutions as shown in Fig. 18. The 942-bar truss problem shows high complexity along with multidimensional characteristics that create a large search area with complex constraints compared to smaller truss structures. MOEHO shows a strong capability to sustain a well-spread and diverse collection of solutions across the Pareto front because it achieves superior Hypervolume (HV) and Inverted Generational Distance (IGD) results. The algorithm maintains strong performance levels regarding convergence and diversity in this complex optimization scenario. The small discrepancy in Fig. 18 does not impact the successful operation of MOEHO. The analysis demonstrates the difficulties of optimizing complex large-scale structures since reference solution alignment becomes progressively harder because of the increasing computational complexity. The robust and adaptable character of MOEHO becomes evident through its generation of diverse well-distributed solutions in complex optimization conditions. The algorithm shows reliable and effective performance for multi-objective optimization through its steady performance across multiple truss structure problems (refer to Figs 11,12,13,14,15,16,17). The future development of MOEHO will prioritize both improved convergence properties for dimensional issues and adaptive control to optimize large optimization challenges. Future developments will enhance MOEHO by making the Pareto solutions more compatible with reference fronts in complex problems without compromising its ability to preserve diversity and computational speed.

However, as the designs for trusses became increasingly complex, the Pareto front envisioned greater dispersion between the two objectives; this proved difficult in complex domain of optimization. The hypervolume (HV) is used as an important parameter for assessment of convergence and diversity among algorithms. Simpler truss structures produced high HV values with relatively low computational effort, proving efficient optimization with least resource requirements. In contrast, the optimization of more complex trusses, such as the 942-bar structure, required significantly greater computational effort, with evaluation counts escalating substantially. This underscores the growing challenge of maintaining both convergence and diversity as the complexity of the design space increases. The results reveal that as truss complexity grows, many algorithms strive to sustain well-distributed Pareto fronts, particularly due to the increased difficulty in navigating conflicting objectives and a more robust optimization landscape. Remarkably, MOEHO consistently performed better than other algorithms across all configurations, particularly in complex circumstances. It demonstrated fine capabilities in maintaining a well-converged and diverse Pareto front, making it highly efficient for addressing high-dimensional, multi-objective truss optimization challenges.

Convergence analysis through HV Matric

Hypervolume (HV)

“Let ${a}^{r}$= ${({a}_{1}^{r},\dots ,\text{a})}^{T}$, be a inferior point dominated by all the Pareto optimal objective vectors. The HV of P is defined as the volume of the objective space dominated by solutions in P and bounded by ${a}^{r}$.

$$\text{HV}(\text{P})=\text{V}(\bigcup_{z\in P}\left[{z}_{1},{Z}_{1}^{r}\right]X\dots X\left[{z}_{m},{Z}_{m}^{r}\right])$$

(12)

where V indicates the Lebesgue measure. Hyper Volume assesses the section of the objective space occupied by the non-dominated solution set; higher values indicate better performance”⁶².

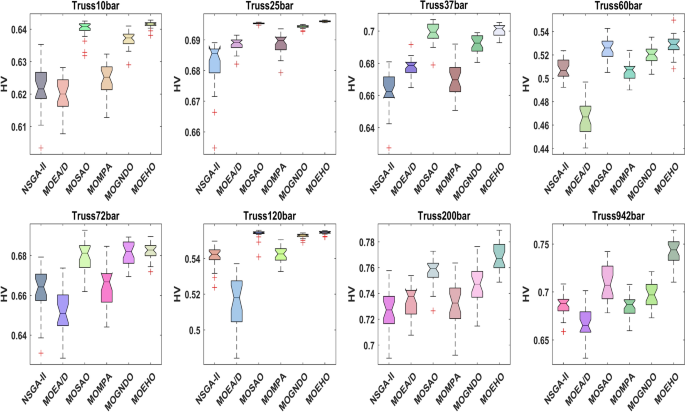
Boxplots provide useful information about the mean and distribution of hypervolume (HV) obtained for each algorithm over several runs, making them a powerful tool for visual algorithm analysis and optimization. Each box shows the median HV value, and the line inside the box represents the interquartile range (IQR) around the middle 50% of the data. The colour of the result depends on the combination of HV input, allowing a direct comparison between algorithms. Therefore, these boxes summarize the distribution and centre of the HV values ​​and provide a useful distribution pattern that shows the performance of each algorithm. Box plot analysis shows the distribution and structure of HV and shows the reliability and consistency of each algorithm. The boxplot components, including mean HV, difference and output, show the algorithm that produces the best HV. A high HV value indicates that the algorithm can capture many target regions, while a small IQR and a small group interval indicate that the algorithm is reliable and stable. The relationship between compatibility and diversity is important for effective organizational design, and managing trade-offs between competing goals is important.

Figure 19 shows the HV parameters of NSGA-II, MOEA/D, MOMPA, MOSAO, MOGNDO, and MOEHO for a typical truss problem. This shows the ability and strength of MOEHO to produce high quality pareto fronts. Compared to, algorithms such as NSGA-II and MOGNDO, MOEHO show significant improvement over HV, especially for complex problems where computational efficiency and quality of solutions are important. The comparison in these boxes shows that MOEHO is better than other algorithms, achieving the highest average HV and the lowest IQR. The small density in the centre of the boxplots of MOEHO ensures that it can pass through the selected area, find a good solution, and do this without excessive monitoring. In general, MOEHO exhibits better performance in system optimization, especially for complex multi-objective problems that require robust, diverse, and well-organized solutions.

Fig. 19

Box plot of hyper volume by considered algorithms for different truss structures.

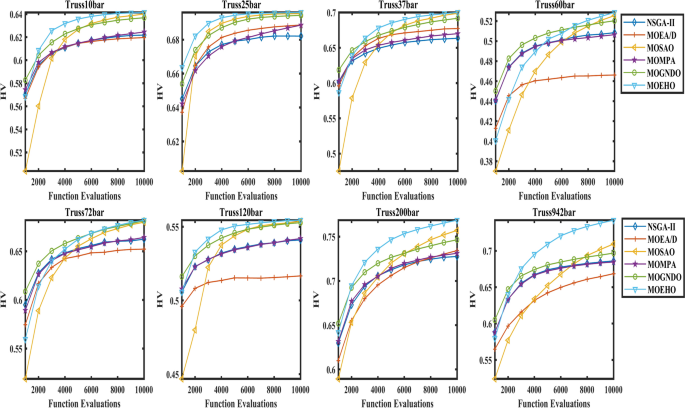
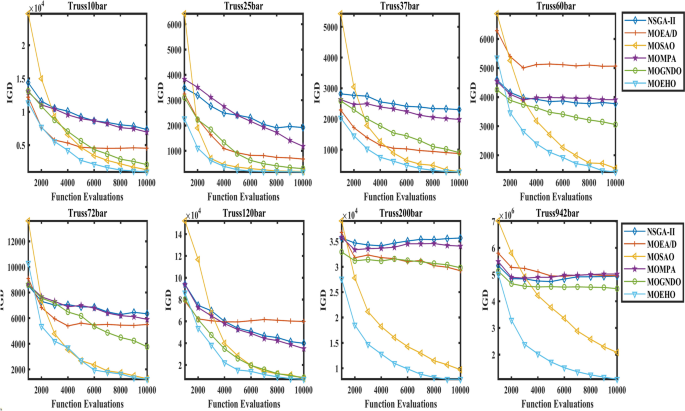
Figure 20 illustrates the hypervolume HV trends observed across eight benchmark constraint-based design problems by comparison of accomplishment of MOEHO with several multi-objective evolutionary algorithms (MOEAs), including NSGA-II, MOSAO, and MOGNDO. These results imply that MOEHO is performing better, with faster convergence and higher final HV values than in previous studies, across all benchmark problems.

Fig. 20

Convergence plot of hyper volume by considered algorithms for different truss structures.

The MOEHO convergence curve reveals that it is possible to rapidly find early high-quality solutions, as well as accurately estimate the Pareto-optimal front in the early stages of the optimization process. This early ‘lead’ in performance is ahead of the other algorithms, thus confirming the superiority of MOEHO in quality and diversity of the solution obtained. The MOEHO algorithm’s structure enables it to cover a large portion of the solution space while offering a good balance of two or more conflicting objectives with great precision. Exploration of objective space over the course of iterations is, thus, vital for multiobjective optimization. Given complicated solution spaces, the adaptive approach of MOEHO indeed proves to strengthen it to obtain optimality of a solution largely.

The above plots indicate the HV convergence of MOEHO to be more statistically higher than other algorithms. This shows support convergence with lesser iterations while providing uniform exploration of multi-dimensional objective space. In comparison with other algorithms, most of the times it tends to output variable solutions in the HV, and the MOEHO has got very nice and smooth transitions showing its ability to find the best solutions.By achieving fast convergence, excellent diversity, and the ability to adapt varied constraint environments, the MOEHO proves to be highly effective for complex multi-objective optimization problems. Its robust performance makes it particularly fit for answering challenging advanced engineering design challenges.

The Hypervolume (HV) values in Table 2 show the performance of MOEHO across different constraint classification problems, by comparison of its performance with other multi-objective optimization algorithms under the difficulty of the classification. For the simple 10-bar algorithm, MOEHO obtained a HV of 0.64142, a value higher than that reached by other algorithms, showing its first step in generating a well-distributed solution set. This trend continues with the 25-bar truss, where MOEHO achieved a HV of 0.69606, in line with its peers. As complexity rises with the 37-bar truss, MOEHO maintains its advantage, achieving an HV of 0.70015. This consistent performance signals MOEHO’s ability to cover the objective space effectively while maintaining high solution quality. For the 60-bar truss, MOEHO demonstrated robust performance with an HV of 0.52869, indicating its adaptability to handle larger structural design challenges without compromising on efficiency.

Table 2 Hypervolume of various Truss structures for different algorithms under consideration.

In the case of a 72-bar truss, MOEHO achieved a hypervolume (HV) value of 0.68197, maintaining its consistent performance in terms of convergence and diversity when compared to other algorithms. This trend continued with the 120-bar truss, where MOEHO recorded an HV of 0.55443, further confirming its capability to deliver high-quality solutions even as the complexity of the truss structures increased.

The accuracy and reliability of MOEHO tend to greatly improve with the increasing complexity of the optimization problem in consideration. Regarding the 200-bar truss, MOEHO recorded an impressive hypervolume (HV) value of 0.76864, proving its capability of exploring and optimizing even in quite large design space. This advantage was affirmed during the execution of the highly complex problem of the 942-bar truss, where the value of the hypervolume generated by MOEHO algorithm was HV = 0.74213, which is better than that of all other algorithms under consideration. These findings demonstrate that MOEHO can provide optimization services in an effective and dependable way even in most complex problem situations.

As shown in the Table 3, MOEHO steadily attained the highest HV across all assessed truss configurations emphasizing its superior convergence and Pareto front solutions diversity. This consistent execution illustrates its efficiency and versatility in solving problems of structural optimization. MOEHO’s ability to optimize with respect to different levels of problem difficulty, proves it as an effective algorithm for multi-objective optimization in structural engineering.

Table 3 showcases the remarkable strength of the MOEHO algorithm as the best performing algorithm for benchmark truss optimization problems considered in the research. Looking at the 10-bar truss, MOEHO records an excellent mean rank of 5.6667 which is much higher than the competing algorithms, with MOEA/D identified as the next best. The trend persists in the 25-bar truss where MOEHO also attains number one position with a score of six confirming its competent in higher order problems. For the 37-bar truss problem, MOEHO has an effective rank of 5.4444 which is still better than the performance of rival methods. When solving the 60-bar truss problem, the associated rank for MOEHO is 5.2963 demonstrating again its capability of producing best optimization results. The same trend persists in the 72-bar truss problem where MOEHO possesses a rank of 5 as well, further reinforcing its dominance in comparison to even the MOSAO approach. For 120-bar trusses that are even more intricate, MOEHO’s rank of 5.4074 indicates some upper hand over MOEA/D as it is also able perform well on more difficult optimization problems as well.

Table 3 P Values and RANK of various Truss structures for different algorithms under consideration.

This dominance has also been observed in the problem concerning the truss of 200 bars when most of the time the algorithm obtaining the rank 2 is MOEHO and the rank of this algorithm is 5.7037. And also exhibited in the analysis of the 942-bar truss problem, the most complicated one assessed, the ranking assigned to MOEHO was the highest at 5.7778 indicating its effectiveness in solving very complicated structural designs. Five additional algorithms are compared to MOEHO: NSGA-II, MOEA/D, MOGNDO, MOMPA, and MOSAO, employing the mean ranks over eight test sets. Data collected from such a case supports the statistical rankings conferred, with p-values between 8.84E-25 and 2.60E-16, stressing the significance of the MOEHO performance. These low p-values confirm the algorithm’s.

Diversity analysis by IGD metric

“Inverted Generational Distance: Assuming P* is the set of points evenly spaced on the Pareto front, P as the solution set obtained from an EMO algorithm. The Inverted Generational Distance (IGD) of the set P is given as follows:

$$\text{IGD }(\text{P},\text{ P}*) =\frac{\sum_{z\in P*}dist(z,P)}{\left|P*\right|}$$

(13)

where dist (z; P) is the distance in Euclidean space from the point z to the closest point of the set P. To perform this calculation, however, it is necessary to sample enough points from the PF to construct P*.”

Inverted Generational Distance (IGD) is an evaluation metric that computes the distance between a given generated Pareto front and the true Pareto front by determining the average distance between the points of the given generated Pareto front and the closest points of the true Pareto front. It is better to say that lower IGD values signify better convergence, which means that generated Pareto front solutions are close to the true Pareto front. This parameter is often employed for the evaluation and implementation of multi-objective optimization techniques as it offers a quantitative measure of how close the estimated Pareto front is to the considered ideal Pareto front⁶³.

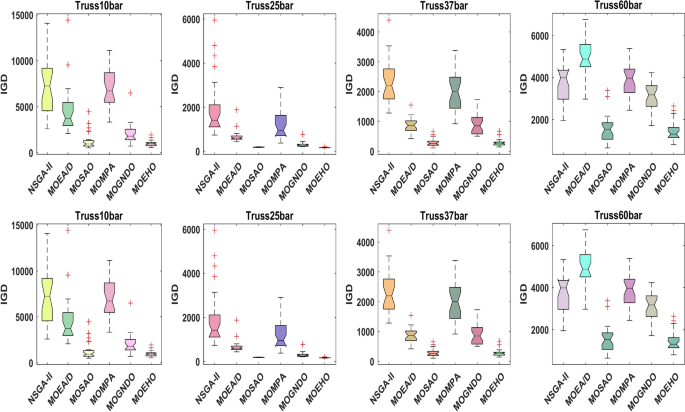
Boxplots present a simplified but effective depiction of the performance of the algorithm in a way that allows understanding both performance over time and the extent of the performance across time. With specific regard to Inverted Generational Distance (IGD), the use of boxplots provides an effective means of depicting the performance of algorithms on various ranges of truss design optimization problems. Policymakers can use comparisons involving boxplots to evaluate algorithm reproduction, performance variability and outliers, for example. Rather this analysis assists to detect those algorithms which do not only perform well but can be relied upon to give a close estimation of the True Pareto front.

In the evaluation of the boxplots, an algorithm that has a consistently less median IGD, a low value in the interquartile range (IQR), and few if any outliers for every truss design problem, will have good stability and good reliability. Such algorithms perform better when it comes to the task of moving along the Pareto front, and hence solve both trivial and sophisticated optimization problems with ease. The advantage of boxplots, in gauging how potent the algorithms are, is that they are used to record how well two performance metrics are sustained across different degrees of complexity of the design problems from the easiest to the toughest. Such a system of evaluating and comparing the efficiency of different algorithms is quite useful to engineers in determining the appropriate algorithm for a particular design work.

The boxplots represent results of the different configurations of the truss in such a manner that it includes Truss10bar, Truss25bar, Truss37bar, Truss60bar, Truss72bar, Truss120bar, Truss200bar and Truss942bar. This graphical representation analyses the performance and its deviation of the algorithms and complements other views of the Algorithm’s effectiveness including the overview of their use on truss optimization problems as shown in the Fig. 21.

Fig.21

Box plot of IGD values by considered algorithms for different truss structures.

The Inverted Generational Distance (IGD) is a decisive metric for evaluating the effectiveness of solutions in approximating the True Pareto front. A lower IGD value implies a closer position of the obtained solutions to the optimal front, implying better convergence and solution quality. In the Truss10bar optimization problem, MOEHO exhibits a remarkably low median IGD, featuring its strong convergence capabilities in simpler truss structures. Its boxplot shows the lowest IQR value among the algorithms, meaning a consistent performance with least variability between iterations and problems. In contrast, MOMPA and MOSAO have wider distributions of IGD, which imply failure to converge towards the Pareto front. MOEA/D, MOGNDO, and NSGA-II have higher values of IGD and wider spreads, which suggest that they cannot reliably approximate the optimal solutions.

Furthermore, this is further enhanced with the dominance of MOEHO in solving the Truss25bar problem. It showed the smallest median IGD and IQR, therefore, ensuring the stability and its repeat ability of generating high quality solutions. The MOMPA and NSGA II could not deliver on convergence, as the boxplots that had a larger area with outliers show many inconsistencies for efficient convergence toward the Pareto front. These outliers indicate the presence of a wide range of performance variability, while for MOEHO, the tight IQR in addition to the low median IGD indicated the potency of the algorithm in handling problems at any level of complexity. For Truss37bar, MOEHO persists with its superior performances. It becomes excellent in the treatment of structural optimization problems of moderate complexities that further ascertain its ability in dealing with challenging design landscapes. The Truss60bar configuration has very low median IGD and a narrow IQR; it is quite reliable concerning the handling of more challenging optimization tasks. The increase in problem complexity by means of larger design spaces and more constraints generally results in the fact that median IGD values for all algorithms increase. This pattern is very clear in the Truss72bar problem, where MOEHO continues to stand out by having a low median IGD and minimal variability, thus demonstrating consistency in producing reliable solutions despite increased complexity.

In the Truss120bar problem, the optimization task is more persistent. Although MOEHO achieves a competitive median IGD, its IQR expands by a small amount. Again, an increase in variance across all algorithms will be noted when applying the algorithms to more difficult problems. Even with this minor increase, MOEHO remains an assured performer. In the Truss200bar configuration, MOEHO again does a good job to achieve a low median IGD, though IQR increases a little. The results confirm that MOEHO is consistent in generating solutions close to the Pareto front even in large-scale structural optimization problems. Its performance is reflected in its adaptability and reliability in dealing with high-dimensional and constrained design optimization problems.

The Truss942bar problem is the most complex benchmark of the present work. Even at its extreme complexity, MOEHO displays a relatively low median IGD, just with a limited extension of the IQR. On the contrary, the distribution of the competitive algorithms shows more elevated IGD values, spreads, and an increased number of outliers, signalling that convergence might be problematic, especially for so difficult a problem. The performance of MOEHO on this complex problem highlights its amazing sturdiness and adaptability, making it a dependable algorithm even under the most challenging optimization conditions.

Consistent results with slight variability made MOEHO a dependable option for the solving of intricate problems in truss design optimization. The performance metrics of various MOOAs integrated in NSGA-II, MOEA/D, MOMPA, MOGNDO, MOSAO, and MOEHO, which are compared with the performance of the eight benchmark truss structure problems as shown in Fig. 22 while the benchmark problems are composed of a simple 10-bar truss problem and the most complex 942 bar truss problem. Plot of the increase in Inverted Generational Distance (IGD) values with an increase in function evaluations. IGD values lower are better since it more approximates the True Pareto Front, hence solutions obtained are of better quality and convergence.

Fig. 22

Convergence plot of IGD by considered algorithms for different truss structures.

Looking at the results, some algorithms seem to have a higher rate of convergence, that is, lower IGD values are realized with fewer function evaluations. The performances of MOEHO and MOSAO will always be at the upper range especially with respect to simple structures like the 10-bar and 25-bar trusses. They also exhibit a quick decrease in IGD and can get optimal solutions in a short time compared to others. However, this is not the case for MOMPA and NSGA II as they have a tendency of achieving lower convergence rate even with the simpler trusses. In the 200-bar and 942-bar trusses complex problems, the IGD values are still high indicating a poor approximation towards the Pareto front.

MOEHO outperforms others in all truss problems. Its IGDs remain minimum against the function evaluation over the problem complexity periphery. This behaviour reinforces the observations concerning the efficiency of MOEHO in addressing any given optimization problem. In addition, the way it achieves solutions within a short period of time with high accurateness for structural optimization problems makes this algorithm unique. On the other hand, while MOEA/D can compete well in simple designs problems. The ability of MOEHO to endure such simple and very complicated trusses designs illustrates its flexibility.

The results demonstrated in Fig. 22 illustrate more clearly the benefits of using MOEHO for multi-objective structural problems, its convergence curves show that the rate of convergence was faster and yet more stable. MOEHO produces diverse as well as the accurate approximations of the Pareto front. From these results, it may be concluded that MOEHO is an efficient and effective multi-objective truss design optimization algorithm.

Table 4 contains a comprehensive evaluation of the efficiency of MOEHO in the solution of the benchmark truss optimization problems anchored on the Inverted Generational Distance (IGD) metric. For the simple optimization problems such as the 10-bar truss, the algorithm exhibited an IGD of 9.5271e + 2. This illustrates MOEHO’s effectiveness in handling simple structural optimization problems. The algorithm is reliable and capable when dealing with simple truss structure problem–solution. The same is true for the problems that are slightly difficult, for instance, the 25-bar truss problem which had an IGD value of 1.6456 e + 2 for the MOEHO. This is a good demonstration of the method’s adaptability and robustness to handle the more challenging optimization problems and to perform well. For more complex structures within the moderate range, such as the 60-bar and 72-bar trusses, MOEHO attained IGD values of 2.7386 e + 3 and 1.4243 e + 3, respectively. It can easily be observed that the algorithm performed efficiently in solving the challenging optimization problem of approximating the Pareto optimal front.

Table 4 IGD of various Truss structures for different algorithms under consideration.

In problems of very high complexity, MOEHO’s real strength can be observed. For the 942-bar truss structure, the algorithm has an IGD value of 1.0793 e + 6, indicating that it is capable of handling complex optimization problems. These results highlight the flexibility and robustness of MOEHO in handling different levels of problem complexity. Despite MOEHO’s inability to regularly provide the least IGD for each test, its efficiency in finding approximate solutions makes it more suitable for addressing challenging optimization tasks. The overall performance of this algorithm indicates how reliable and versatile it is. This makes MOEHO an efficient tool to solve multi-objective structural optimization problems.

Table 5 gives an extensive analysis of rank based on IGD values and comparison of p-values for MOEHO and various MOOAs over 8 different truss optimization problems. The p-values show the statistical significance of MOEHO performance, which proves its efficiency when is used in optimization problems. For example, during the solution of the 10-bar truss problem, MOEHO algorithm was ranked 1.5161 and scored a p-value of 4.16E-25 giving strong significance. This general tendency is also observed in more complicated issues such as the case of 25-bar and 37-bar truss configurations where the ranks were 1.0968 and 1.6129 respectively and p-values were 1.11E-28 and 1.63E-27. These results clearly indicate the superiority of MOEHO over its competitors in different kinds of optimization processes.

Table 5 P Values and Rank based on IGD of various Truss structures for different algorithms under consideration.

As the Tusse structures become more complex, the MOEHO keeps giving better outcomes. For instance, consider the 60-bar and 72-way trusses. The observed p values of 1.08E-24 and 8.61E-24 respectively shows a significant effective difference in favour of MOEHO. In the complex 942-bar truss problem almighty MOEHO scored a p-value of 6.81E-24 again reinforcing its effectiveness under extreme cases. The presence of this pattern of p-values, which are quite low for many problems, is further indicative of the applicability of MOEHO computational tool in multi-objective truss optimization to be carried out optimally.

Moreover, the Friedman test ranks analysis shown in Table 5 also helps to view the performance of MOEHO in quantitative terms. Scores in the Friedman test are inversely related to performance with MOEHO scoring 1.5143 in 10-bar truss problem indicating best performance on simple problems. In the case of 60-bar truss problem, MOEHO scored 1.5429 confirming it as excellent performer. Despite the intricacies of the 942-bar truss problem, MOEHO earned a 1.1714 score evidencing its efficiency in solving complex optimization problems that are very difficult to solve.

From these observations, it can be inferred that besides ease of use, MOEHO is a flexible and strong tool when it comes to optimization procedures. Given the fact that it consistently records lower IGD values in addition to strong statistical performance in numerous truss setups, MOEHO is an effective optimization algorithm for solving complex problems in multi-objective optimization. MOEHO is combined with encouraging statistical results and effectiveness in its computation making it suitable for use by design engineers and researchers to solve problems in structural optimization.

Quality assessment of non-dominated solutions by spacing matrix

“Spacing (SP) measures the evenness of spacing between adjacent solutions along the Pareto front, aiming for a balanced distribution without clustering or excessive gaps. Lower SP values indicate more uniformly spaced solutions.

$$\text{Spacing}=\sqrt{\frac{1}{{N}_{0}-1}\sum_{i=1}^{{N}_{0}}{\left(mean\left({d}_{i}^{spacing}\right)-{d}_{i}^{spacing}\right)}^{2}}$$

(14)

where, ${N}_{0}$ denoted the number of pareto fronts and ${d}_{i}^{spacing}$ denotes the Euclidean distances between consecutive solutions in the objective space. Spacing assess the spread and distribution of solutions across the Pareto front”⁶⁴.

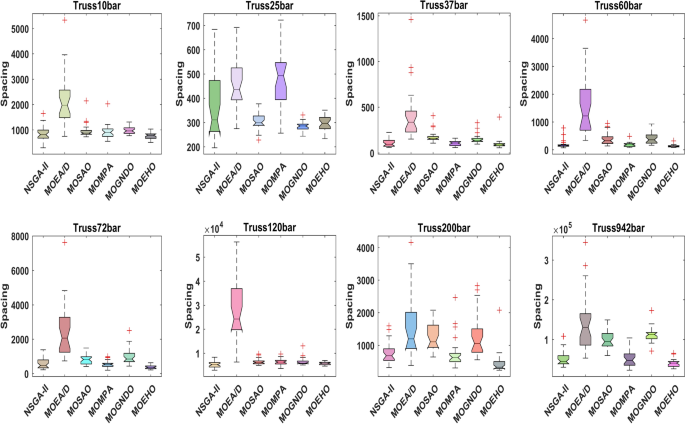
The box plots depicted in Fig. 23 illustrate the SP values corresponding to various optimization challenges in truss structures, as evaluated by multiple multi-objective algorithms, including NSGA-II, MOEA/D, MOMPA, MOGNDO, MOSAO, and MOEHO. The SP metric is an essential indicator of the uniformity of solution distribution along the Pareto front; lower SP values signify a more evenly distributed set of solutions, which is generally preferred in optimization scenarios. MOEHO stands out for its consistently superior performance across all tested truss structures, demonstrating an impressive capacity for both SP distribution and convergence.

Fig.23

Box plot of SP values by considered algorithms for different truss structures.

The boxplots indicate that MOEHO provides more low and stable SP values in comparison to the other methods, which also support a more uniform set of solutions on the Pareto front. This ability of the algorithm is critical to accurately locate the solution point, this helps to improve quality and reliability of the algorithm. The consistency across diverse truss problems and capacity to preserve this uniformity makes MEHO applicable for complex optimization problems.

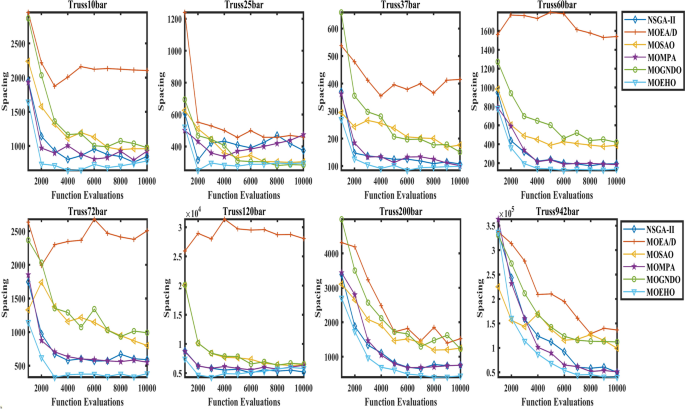
The convergence graph presented in Fig. 24 indicates that MOEHO offers higher speed and a stable solution distribution. The performance analysis of MOGNDO and NSGA-II shows that the convergence rate is slow and the solution’s reliable distribution cannot be achieved when MOGNDO and NSGA-II are used. This result indicates that they lack the capacity to create systemic (widespread) solution on complex problems.

Fig. 24

Convergence plot of SP Values by considered algorithms for different truss structures.

MOEHO’s capability to deliver lower development time, and sustainable solution plays a decisive role in truss design optimization. This capability of MOEHO to search the solution space in an efficient manner to yield diverse solutions for optimization problems of varying complexity makes it suitable for the multi-objective optimization problems of truss structures.

SP is quite important for multi-objective optimization since it measures the evenness of how the solutions are spread in the Pareto front. Very low values of SP suggest a good and desired distribution of solution set for optimum performance improvement. In optimization problems, uniform distribution is necessary because optimally it permits full representation of the Pareto front, since solutions are not overly dense in any area, but rather well and evenly spread throughout the solution space. A Comparative study of the SP values of some Algorithms: NSGA-II, MOEA/D, MOMPA, MOGNDO, MOSAO, MOEHO for several truss optimization problems shows how these algorithms could distribute the solutions satisfactorily. The SP results are presented in Table 6, where the MOEHO outperforms all other truss design problems considered.

Table 6 The SP of various Truss structures for different algorithms under consideration.

As an example, in the 200-bar truss problem, the MOEHO algorithm yields a SP value of 4.3566e + 2, while for the second-best method, MOMPA is equal to 7.7962e + 2. Since the SP value is considerably low for MOEHO, it can be presumed that the solutions proposed by MOEHO are more diversified and extended along the curve of the Pareto front, even in the more complicated and higher-dimensional optimization problems. It can therefore be inferred that the MOEHO executes its task extremely well. The MOEHO produces the solutions which are widely scattered even in the challenging situation, which is a major requirement to guarantee full optimization.

The difference in SP values between MOEHO and the rest of the algorithms confirms that the other algorithms generate more clustered solutions, which are indicated by higher SP values. Such clustering tendencies would hinder the comprehensive nature of optimization algorithm. A statistical evaluation of p-values shows the effectiveness of MOEHO in comparison with other state of the art constrained multi objective optimization techniques used on eight different truss designs. Analysis of the statistics produced p-values between 1.30E-24 and 6.14E-15 implying that the observed differences in the relative SP performance are very large.

Such statistical evidence strengthens the assertion that MOEHO is better than competing algorithms at generating solutions which are evenly spaced on the Pareto front. Such a benefit also demonstrates the potential of MOEHO in solving complex multi-objective optimization problems, particularly in design processes where the solutions must be evenly spread out and the entire solution space must be utilized. This spanning superiority is consistent with how spaced this algorithm is, proving its strength and the optimum and dependable solutions it can render within many optimization problems.

Table 7 displays the outcomes of the Friedman rank test, showcasing MOEHO’s impressive performance with consistently lower average ranks across various truss design challenges using the SP metric. These lower average ranks signify MOEHO’s superiority in maintaining a diverse and well-distributed range of solutions, crucial for efficient multi-objective optimization in intricate engineering scenarios.

Table 7 P Values and Rank based on SP of various Truss structures for different algorithms under consideration.

The favourable ranks achieved by MOEHO affirm its capacity to generate a broad spectrum of solutions that are appropriately distributed along the Pareto front the notable difference in ranks, supported by high P-values, underscores MOEHO’s dominance over its competitors concerning solution SP. This exceptional performance underscores MOEHO’s effectiveness in handling solution diversity, a vital aspect for the reliability and adaptability required in tackling intricate structural engineering design and optimization issues. The capability to produce a varied set of solutions not only enriches decision-making quality but also ensures a thorough exploration of the solution space.

The computational runtime for different truss structures across various algorithms reveals significant variations, particularly for complex structures with a higher number of elements. While NSGA-II demonstrates the highest runtime in most cases, MOEHO and MOGNDO exhibit relatively lower computational costs for larger structures, indicating their efficiency in handling increased complexity as shown in the Table 8.

Table 8 The Runtime of various Truss structures for different algorithms under consideration.

In MO optimization, it is generally a compromise between efficiency and solution quality. Although Table 8 indicates that MOEHO is not always the quickest algorithm, its slightly longer runtime is worthwhile for its better convergence performance, evident in the HV, IGD, and SP metrics. The extra computational expense comes from MOEHO’s adaptive strategies, such as dynamic parameter adjustment and an information feedback approach, that promote exploration and keep a diversified Pareto front. Compared to algorithms such as MOSAO and MOGNDO, they might gain quicker runtimes but may lose in solution diversity and convergence quality. To demonstrate this balance, a comparative study of runtime and performance measures is given, showing that MOEHO provides a better trade-off and, thus, is a competitive option for structural optimization with a moderate rise in computational time.

According to Table 8 the runtime analysis shows MOEHO does not achieve the fastest results for all truss structures. The balance between solution quality and runtime serves as an essential reason to accept MOEHO’s elevated computational costs in particular situations. The runtime performance of MOEHO shows slightly longer durations than MOSAO or MOGNDO for basic structures such as 10-bar and 25-bar trusses but proves its superiority through better solution quality and diversity when dealing with complex optimization problems. MOEHO shows competitive runtime performance across various complex structures such as the 200-bar and 942-bar trusses but produces superior solutions as confirmed through superior Hypervolume (HV) and Inverted Generational Distance (IGD) and Spacing (SP) metrics observations. MOEHO achieves an optimal balance between efficient computing and excellent solution quality which proves beneficial for cases requiring precise robust solutions that adequately explore diverse Pareto fronts.

The ability of MOEHO to maintain proper exploration–exploitation balance in engineering design applications prevents it from converging prematurely towards suboptimal solutions while ensuring solution accuracy and reliability. The success of traditional algorithms to produce diverse accurate Pareto front approximations becomes crucial in high-dimensional optimization problems with constraints. MOEHO’s slightly elevated computational requirements become worthwhile since it produces solutions that both match the true Pareto front more precisely and distribute solutions uniformly which helps decision-makers make confident optimal design selections. MOEHO demonstrates robust performance through adaptive parameter controls together with dynamic strategy-based selection features which enhances its ability to resolve complex engineering problems better than most other algorithms.

The analysis of essential trends in the figure captions delivers a thorough performance review of MOEHO when optimizing truss structures. The 10-bar truss problem in Fig. 11 demonstrates that MOEHO produces superior Pareto fronts than NSGA-II, MOEA/D, MOMPA, MOGNDO and MOSAO while maintaining excellent convergence and diversity. This algorithm produces a well-organized set of solutions that closely follows the true Pareto front because it demonstrates robustness when dealing with small-scale structural optimization problems. MOEHO generates a denser Pareto front for the 25-bar truss problem which spans across a wider area in the objective space as illustrated in Fig. 12. The algorithm proves its capability to solve medium-scale optimization problems while maintaining diverse solutions.

In the 37-bar truss problem of Fig. 13 MOEHO demonstrates a Pareto front with excellent distribution and minimal clustering because it effectively balances exploration and exploitation. The algorithm enhances promising solutions while preserving diversity which makes it suitable for moderately complex structural optimization problems. The MOEHO algorithm demonstrates scalability through its Pareto front generation for the 60-bar truss problem as shown in Fig. 14. The optimization process demonstrates effective handling of complex problems because solutions are distributed evenly while gaps and clusters remain minimal. The MOEHO algorithm demonstrates a uniform distribution of solutions in the Pareto front for the 72-bar truss optimization problem as shown in Fig. 15. The optimization algorithm demonstrates excellent search space exploration capabilities with precise results which makes it suitable for high-dimensional problems.

MOEHO demonstrates its capability to produce a properly distributed Pareto front for the 120-bar truss problem through minimal computational requirements as shown in Fig. 16. The algorithm manages exploration against exploitation activities to yield high-quality and diverse solutions. MOEHO demonstrates efficient performance in large-scale optimization problems through Fig. 17 by maintaining convergence and diversity in the Pareto front when solving the 200-bar truss. The results in Fig. 18 display how MOEHO outperforms competing algorithms with its exceptional ability to optimize the highly complex 942-bar truss system alike its superiority in solution quality alongside computational efficiency. MOEHO generates a Pareto front that spans a wide area of the objective space thus demonstrating its ability to address complex high-dimensional multi-objective optimization problems effectively.

The superiority of MOEHO in truss structure optimization problems becomes evident through Fig. 19 which shows box plots of Hypervolume (HV) values. The superior HV values obtained by MOEHO demonstrate its capability to effectively explore the objective space and create high-quality solutions. The small interquartile range (IQR) confirms both the stability and reliability of the results. Figure 20 illustrates how MOEHO achieves higher Hypervolume values during fewer function evaluations compared to alternative algorithms. The algorithm demonstrates quick discovery of promising search areas during its early optimization period because of its efficient space exploration capabilities.

The assessment of Inverted Generational Distance (IGD) as a Pareto front approximation quality metric occurs in Figs. 21 and 22. The box plots in Fig. 21 show MOEHO produces consistently lower IGD values which proves its superior ability to approximate the true Pareto front with diversity maintained. Figure 22 demonstrates that MOEHO efficiently reaches low IGD values through minimal function evaluations thus proving its ability to solve complex multi-objective problems effectively.

The spacing (SP) values presented in Figs. 23 and 24 demonstrate that MOEHO effectively produces solutions with uniform distribution. Figure 23 demonstrates MOEHO produces lower SP values throughout all trials which indicates its strong capability for maintaining solution diversity. Figure 24 shows that MOEHO finds diverse well-spaced solutions using fewer function evaluations thus demonstrating its efficiency in simultaneously reaching convergence and diversity.

The interpretations detail MOEHO performance trends through evaluations which demonstrate its solid convergence and diverse results and computational efficiency on different structural optimization problems. The algorithm shows potential for extending its application to various multi-objective optimization challenges which surpasses structural engineering fields.

The MOEHO algorithm proved to be successful in solving structural optimization problems of various complexity. It performs best in comparison with other algorithms since it has quality outputs, which are processed faster. The above performance in handling problems of varying complexity shows that MOEHO has practical applications where speed and good-quality results are needed. However, on larger truss structures such as the Truss72bar configuration, MOEHO suffers somewhat in terms of computational speed, but its quality of solution increases with the size of the problem. This balancing of computational speed and solution quality is important for the field of structural optimization where results need to be efficient as well as effective. Although MOEHO has been shown to have excellent performance in structural optimization, its extension to other fields is an open area for investigation. One of the limitations is its computational expense on large-scale problems, which, while compensated by better solution quality, can be further improved with parallel computing or surrogate-assisted modeling. Another area that has not yet been thoroughly investigated is the performance of MOEHO in fields like energy systems, aerodynamics, and robotics. Subsequent studies may entail modifying MOEHO for real-time and dynamic optimization problems and incorporating machine learning-based approaches to improve convergence rates and computational effectiveness, extending its applicability to a wide range of engineering disciplines.

The fact that MOEHO maintains a proper distribution of solutions even when the computational requirements increase reinforces its status as an effective and reliable choice for more complex multi-objective optimization problems. The consistency of MOEHO’s performance with problem sizes underlines its adaptability and robustness, making it a very useful tool for engineers who are dealing with complex structural design tasks. Thus, MOEHO is not only superior in providing solutions but also shows resistance in the face of increasing computational challenges.

MOEHO achieves fastest convergence speed against other algorithms during the optimization of benchmark truss structures. The hypervolume (HV) and inverted generational distance (IGD) metrics show that MOEHO achieves better high-quality solutions more quickly than NSGA-II, MOEA/D, MOMPA, MOGNDO, and MOSAO algorithms. MOEHO demonstrates enhanced early-stage optimization efficiency through its achievement of an HV value of 0.6414 in the 10-bar truss problem before other algorithms reach similar results. The rapid convergence rate of MOEHO continues throughout the optimization process of the 942-bar truss despite its complex structural nature.

The Pareto front diversity of MOEHO is demonstrated through its excellent performance in the spacing (SP) metric. The algorithm generates solutions with equal distribution which leads to complete coverage of the Pareto-optimal set. MOEHO demonstrates superior solution distribution in the 200-bar truss problem through its SP value of 4.4252e + 2 which surpasses alternative algorithms. A diverse set of solutions stands essential for engineering design because it supports better decision-making by providing various trade-offs between competing project objectives. The performance of MOEHO maintains its strength when the truss structures become progressively more complex. In solving the 10-bar truss problem MOEHO achieves superior performance with an HV of 0.6414 and an IGD of 9.6527e + 2 compared to other tested algorithms. The 942-bar truss structure presents no challenge to MOEHO which generates high-quality results with HV at 0.7421 and IGD at 1.0793e + 6. MOEHO displays its ability to expand into high-dimensional problems because of its flexible architecture that maintains operational reliability when handling multi-objective challenges.

The Friedman rank test establishes MOEHO as superior by showing consistently low average ranks in every test scenario. In the 25-bar truss problem MOEHO obtains a ranking position of 6 which demonstrates superior performance compared to other algorithms. The statistical significance of MOEHO’s performance becomes evident through its low p-values which reach 8.84E-25 in the 25-bar truss problem.

The study improves reproducibility by completely explaining MOEHO’s mathematical model which includes Pareto-Dominance Ranking and Crowding Distance Approach and Elite Retention and Adaptive Parameter Settings. The implementation approach includes both pseudo-code and flowcharts to help developers. Future researchers can replicate the findings because this research provides complete information about all algorithm-specific parameters and population size and maximum iterations. The study provides comprehensive descriptions of benchmark problems which include multiple truss structures from 10-bar to 942-bar that specify design variables together with constraints and loading requirements. The study defines HV, IGD, and SP formally to ensure consistent evaluation practices. The conclusions benefit from statistical robustness because the study employs the Friedman rank test together with p-values for validation.

The paper advances previous research through its addition of flowcharts and visual aids which demonstrate the operations of EHO and MOEHO. The optimization results become more understandable through visual representations of Pareto fronts that accompany each truss problem. The mathematical descriptions of MOEHO components including the rutting season and calving season and selection mechanisms appear in a clear fashion to guarantee methodological transparency. The research improves understandability through assessments utilizing boxplots and convergence plots as they display MOEHO’s efficiency through visual charts. The study defines technical terms alongside multi-objective optimization concepts in a way that makes the information understandable for both experts and non-experts in the field.

Conclusion and future scope

Based on its performance in solving challenging problems of multi-objective optimization, especially in engineering design, the MOEHO algorithm is a significant development. This work tests the performance of MOEHO on eight benchmark structural design problems: optimizing truss structures to minimize weight and compliance. MOEHO has demonstrated consistent superiority when compared to well-known algorithms, such as NSGA-II, MOEA/D, MOMPA, MOGNDO, and MOSAO, which demonstrates its effectiveness and reliability. Innovative in search process- MOEHO has one among its main properties, that being a dynamic approach of strategy-based selection. Its inclusion makes possible the convergence towards a point but at the same time keeping much diversity within that solution space as well. Thus, this permits MOEHO to explore a large spectrum of possible solutions but focuses on the best ones at every iteration to gain high efficiency in finding Pareto-optimal solutions and therefore, more profoundly explore the solution space than traditional approaches. From the above representation, its overall performance can also be viewed as being highly competitive especially on the critical Hypervolume (HV) measure which it can capture a large proportion of objective space along the Pareto front. Admirable values of HV scores reflect the capacities of MOEHO in producing high-quality solutions for a variety of optimization problems. Moreover, performance of MOEHO has further been tested using IGD, which is based on the closeness of obtained solutions to the ideal Pareto front.

The low consistently achieved IGD values by MOEHO affirm that the generated solutions are almost exact approximations to the true Pareto front and hence this is efficient with consistency. Good SP metric shows how well uniform is the spread of solutions up the Pareto front. Overall, MOEHO is highly competitive with any of the used algorithms in each scenario of designing a truss and therefore quite scalable and robust in multiobjective optimization. The quality of the overall optimization process improves with uniformity in the solutions by MOEHO, thus ensuring that the Pareto front is well represented. The Friedman rank test for the validation of MOEHO’s statistical robustness was 1.129, which not only proves the superiority of the algorithm but also emphasizes its ability to deliver reliable solutions across a wide range of problem contexts. Moreover, the computational complexity of MOEHO is competitive for solving small to medium-sized truss design problems. This makes it practical and relevant for real-world engineering applications.

For MOEHO, innovative search operators and dynamic strategy-based selection mechanisms are used to further improve the integration between solution space exploration and exploitation of promising regions.

This balanced strategy leads to rapid convergence rates and higher diversity of solutions with optimised runtime performance, making MOEHO an effective tool in constrained optimization for engineering problems. This algorithm helps in the better management of trade-off between exploration and exploitation. In the future, MOEHO might be able to surpass structural optimization in terms of adaptability and resilience toward high-dimensional optimization problems in energy systems, aerodynamics, and other complicated applications in engineering.

Intensive validation of MOEHO based on performance metrics such as HV, IGD, and SP, along with comprehensive statistical analysis, vindicates its status as a reliable, general-purpose algorithm that can be faced for solving real-world multi-objective optimization problems. Further along the road of traversal of the algorithm, in addition, more performance improvements, with a view to widen its applicability, will make it a solution in preference for solving a vast array of challenges toward efficiency and innovation in different industries.

The main drawback of MOEHO exists in its restrictions that apply to specific domains. The structural optimization problems where MOEHO has been tested mainly demonstrate its capabilities while its effectiveness for handling complex evolving constraints found in energy systems and aerodynamics remains untested. MOEHO requires adaptation to handle optimization tasks that need nonlinear dynamical analysis and real-time adjustment capabilities which are common in certain domains. The method faces difficulties when trying to scale up to problems with numerous dimensions. The promising outcomes of MOEHO in truss optimization tasks of small-to-medium scale do not provide clear indications about its ability to maintain diversity and convergence in large-scale problems such as aerodynamic shape optimization and energy distribution networks. The curse of dimensionality affects high-dimensional problems by reducing search efficiency of algorithms. MOEHO faces issues with operational speed as yet another significant challenge. Structural optimization tasks show runnable efficiency with MOEHO but its practical application in demanding applications such as CFD and energy network optimization has not been proven yet. The domain simulations demand high computational power along with notable processing times that might negatively affect MOEHO’s operational speed.

Future investigations should develop several new directions to expand the practical scope of MOEHO. Energy systems optimization represents an opportunity for MOEHO’s practical implementation. Multiple objectives occur within energy problems such as power grid stability and renewable energy integration and energy storage management due to opposing requirements that include cost reduction and efficiency optimization alongside environmental sustainability concerns. Through adaptation MOEHO can enhance the situating and control of renewable energy generation units and energy storage devices and grid stability mechanisms under unstable power supply and consumer patterns. Aerodynamic design optimization benefits from MOEHO because it solves airfoil shaping problems together with aircraft wing optimization by balancing the nonlinear objectives between drag reduction and lift increase and structural performance maintenance. MOEHO requires domain-specific constraints and surrogate modeling techniques to become suitable for handling complex problems.

The combination of MOEHO with machine learning approaches opens new opportunities to expand its efficiency and scalability for big-dimensional optimization issues. Machine learning models including neural networks along with Gaussian processes would integrate with MOEHO to produce approximations of costly objective functions which shortens processing duration without reducing solution quality. MOEHO requires modification to support dynamic and real-time optimization needs which enables its application in systems that need continuous re-optimization such as real-time energy management and adaptive control systems. The adoption of dynamic solution adjustment capabilities in MOEHO according to changing constraints and objectives would boost its practical application potential.

The general applicability of MOEHO should be confirmed through extensive testing on multiple optimization problems from different fields. Extensive testing of MOEHO on problems beyond structural optimization will reveal its performance characteristics across different scenarios and lead to required improvements. The method requires thorough examination of how algorithm parameters affect the optimization process. The robustness of MOEHO in structural optimization exists but its performance across other domains might require precise adjustments of bull rate and adaptive factors. More thorough parameter sensitivity tests would permit adjustments to maximize performance quality across different application scenarios. MOEHO integration with multi-physics simulations would allow its use for problems involving multiple physical domains like fluid–structure interaction and thermal-fluid dynamics. Future research in this area should focus on MOEHO as a potential solution because it handles complex multi-disciplinary problems with diverse constraints.

Future development of MOEHO through addressing its challenges and exploring new directions will make it a more versatile optimization tool that serves multiple engineering and scientific applications. The practical application value of MOEHO increases while its contribution to multi-objective optimization methodology development supports its effectiveness in solving complex real-world problems.