Bifurcation analysis and dynamical behavior of novel optical soliton solution of chiral (2 + 1) dimensional nonlinear Schrodinger equation in telecommunication system

Abstract

This study explores in detail the bifurcation and optical solitons of the third-order nonlinear chiral (2 + 1)-dimensional nonlinear Schrödinger equation (M-fCNLSE) with the M-fractional derivative in nonlinear media. We also discuss the properties of fractional derivatives in this context. Initially, bifurcation theory is utilized to analyze critical points and phase portraits, identifying transitions that give rise to new dynamical behaviors, such as stability shifts or the onset of chaotic motion. The first figure depicts the dynamics of soliton solutions undergoing a saddle-node bifurcation. There are two techniques, namely the polynomial expansion (PE) and the unified solver (US) techniques, that are applied to explore wave propagation in telecommunication systems, nonlinear optics, plasma physics, and quantum mechanics. These methods enable the creation of new optical soliton solutions using hyperbolic, rational, and trigonometric functions. Numerical results, presented in 2D and 3D diagrams, demonstrate the behavior of the solutions. The polynomial expansion technique generates diverse periodic optical soliton solutions, including double-periodic and lump wave solitons. The unified solver technique produces periodic breather waves, double-periodic waves, and other complex wave structures. Additionally, two-dimensional graphs display the effects of the truncated M-fractional parameters for $P=0.1, 0.5, 0.75, 0.9$. Overall, this investigation and the proposed techniques provide valuable tools for generating precise optical soliton solutions, which have significant applications in optical communications, nonlinear optics, and engineering.

Introduction

In the last decade, the research study designates that optical soliton wave pattern may symbolize a viable alternative for transmission with ultra-long-distance and high-capacity. From its experimental remark by Mollenauer in 1980 and its prophecy by Hasegawa in 1973^1,2,3, optical solitons have been the focus of extensive research. Actually, a solitary wave solution is an alternative form of soliton solutions that traverse propagation dimension deprived of run into any interference. Some interface procedures arise during the optical wave propagations due to the space are decreased between adjacent of optical solitons, the transmission speed and in high-speed communication system communication capacity are increased. Many researchers used optical soliton waves that transmit data across multiple channels in Communication systems^1,2,3,4,5, etc.

In present internet data, the most important infrastructure is the optical communication system. The optical fiber communication system is useful to the evolution and operation of long-distance communication networks, which have the benefits of long-distance broadcast with negligible signal damage and extremely high data-carrying capacity. The nonlinear models serve as mathematical frameworks that integrate diverse phenomena in optical fiber, fluid mechanics, nonlinear optics, and plasma physics^6,7,8,9,10. The increasing amount of study on solitons has led to a significant number of researchers concentrating on this area. Soliton solutions derivation, modeling of various natural physical processes, and solving nonlinear models have all gained a unique domain and importance. As a result of these investigations, certain disciplines have firmly adopted specific techniques and methods, while new approaches to problem-solving have emerged. Among the techniques are unified technique¹¹, sub-equation method¹², NMSE technique¹³, EMSE technique¹⁴, MHFE technique¹⁵, the (G′/G)-expansion technique and the GK technique¹⁶, Hirota bilinear method^17,18, modified auxiliary equation scheme¹⁹, MSE technique²⁰, NMH technique²¹ Generalized exponential approach²², Fan sub-equation (PFS-E) method²³, EMSE technique²⁴, the ${\Phi }^{6}$ Method²⁵ and^26,27,28,29.

This study investigates the bifurcation analysis and dynamic conduct of optical soliton for the M-fCNLSE in the specified form:

$$i{D}_{M,t}^{P, n}G+a ({G}_{xx}+{G}_{zz})+i \{{b}_{1} (G{G}_{x}^{*}-{G}^{*}{G}_{x}) +{b}_{2} (G{G}_{z}^{*}-{G}^{*}{G}_{z})\}G=0.$$

(1)

In Eq. (1) ${D}_{M,t}^{P, n}G$ is the evolution tenure, while $a$ embodies the quantity of dispersion, and ${b}_{1}$ and ${b}_{2}$ are the quantities of nonlinear coupler terms.

There are many researchers have investigated diverse solutions and applied different analytic methods. For example, Ghanbari et al. studied soliton solutions of conformable chiral (2 + 1)-D NLS model by GERF technique³⁰, Raza and Javid investigated dark and dark-singular solutions of chiral (2 + 1)-D NLSE by using EDA and ETE scheme³¹, Rehman et al. applied new EDAM and EHF method to solve the 2D CNLSE equation and integrate new soliton form³², Eslami applied the trial solution technique to (1 + 2)-dimensions CNSE equation³³, Awan et al. integrated (2 + 1)D CNSE and found multiple soliton pulse by functional variable technique and first integral technique³⁴, Javid and Raza used exp $(-\varphi (X))$-expansion and MSE scheme for Chiral solitons of the (1 + 2)-D CNSE³⁵, Abdelwahed et al. studied the Stochastic form of CNLSE by the sine–Gordon expansion technique to find the features of soliton wave pattern³⁶, Albosaily et al. applied Riccati–Bernoulli sub-ODE, He’s variational and sine–cosine approaches for the (2 + 1)-Dimensional Stochastic Chiral Nonlinear Schrödinger Equation³⁷, Rezazadeh et al. investigated exact solution to the (2 + 1)-D CNSE by using extended rational sin-cos and sinh-cosh technique³⁸, Bulut et al. investigated dynamics of soliton solutions in CNSE by sine–Gordon expansion method³⁹, Tariq et al. applied EMAEM and improved F-expansion and the unified techniques to (2 + 1)D CNSE⁴⁰, Tala-Tebue et al. investigated the solitons of the (1 + 1) and (2 + 1)-Dimensional CNSE with the Jacobi Elliptical Function Method⁴¹, while Hosseini et al. utilized the modified Jacobi Elliptical Function Method⁴².

The main goal of this study is to utilize bifurcation theory to analyze the critical points and phase portraits of the M-fractional chiral (2 + 1)-dimensional nonlinear Schrödinger equation, focusing on system transitions to new behaviors, including stability shifts and the emergence of chaos. To examine the solitary wave solutions and the impact of fractional derivatives, we employed polynomial expansion (NPE) and unified solver techniques on the M-fCNLSE. Furthermore, we illustrate the complex behaviors of the obtained solutions through three-dimensional, two-dimensional, and density diagrams. The influence of the fractional parameter is depicted in a two-dimensional diagram.

The work has been prescribed as the subsequent order:

Section “Truncated M-fractional derivative” elaborates on several assets and characteristics of the fractional operator.

Section “Methodology” presents the resolution methodology for NLEEs utilizing PE and US approaches.

Section “Mathematical analysis” provides the mathematical elucidation of the proposed model.

Section “Bifurcation analysis” delivers the stability and their phase portrait using bifurcation theory.

Section “Analytic optical soliton solution” employs the PE and US methodologies to derive optical soliton solutions for M-fCNLSE.

Section “Figure analysis” provides the fraction effect and dynamic analysis of optical wave patterns.

Section “Comparison and novelty” offers a comparison and the novelty of this work.

Section “Advantages and limitations of the proposed methods” provides the advantages and limitations of the MSE method for solving NLEEs.

Finally, section “Conclusion” provides a summary of the conclusion.

Truncated M-fractional derivative

Fractional derivatives are crucial for enhancing the efficacy of nonlinear models in diverse study fields. In contrast to conventional integer-order derivatives, fractional derivatives can incorporate memory effects and long-range dependencies, yielding a more precise depiction of intricate real-world systems. Their primary value is in their capacity to represent nonlocal interactions, enabling researchers to examine processes that span many spatial and temporal domains. This capacity is especially beneficial for examining anomalous diffusion and non-integer scaling tendencies, frequently encountered in both natural and artificial systems. Moreover, the use of fractional derivatives also makes nonlinear models more adaptable to showing complex behaviors. Researchers can better understand nonlinearities and memory effects in many fields by using fractional-order variables. These fields include physics, biology, socioeconomics, engineering, control systems, and mathematical physics^{43,44,45,46,47,48,49}. A developing field of research focuses on the exploration of solitary wave solutions, with the truncated M-fractional derivative receiving considerable interest. Research demonstrates that this derivative offers a more accurate depiction of solitary wave dynamics in some nonlinear systems than alternative fractional derivatives. This feature renders it very advantageous in scientific and engineering domains, such as electromagnetics, fluid dynamics, and signal processing. There are numerous fractional derivatives, including the Riemann–Liouville, Caputo, Atangana–Baleanu, conformable, and He’s fractal derivative, that have been extensively utilized in diverse contexts to characterize memory effects, hereditary features, and nonlocal behaviors in physical and engineering challenges^48,49. In this study, we select the M-fractional derivative for its beneficial characteristics in addressing nonlinear evolution equations. This derivative is especially advantageous for maintaining the essential properties of the original equation while integrating fractional-order effects, rendering it appropriate for the analysis of soliton dynamics and wave propagation in intricate media. The M-fractional derivative provides versatility in mathematical expressions and preserves a balance between local and nonlocal characteristics, which is crucial for accurately representing realistic physical processes^50,51,52,53. Consequently, the selection of the M-fractional derivative is warranted due to its capacity to yield more precise and physically significant solutions within the specified problem context.

Definition of M-fractional derivative

Consider $\Xi :\left(0, \infty \right)\to {\mathbb{R}}$ the TMD of $\upchi$ with order $n$ exhibit as:

$${D}_{M,t}^{P, n}\Xi \left(t\right)=\underset{h\to 0}{\mathit{lim}}\frac{\Xi \left(t{H}_{n}\left(h{t}^{1-P}\right)\right)-\Xi \left(t\right)}{h}; \quad 0<P<1, n>0.$$

We will now elucidate the characteristics of the truncated M-fractional operator ${D}_{M,t}^{P, n}$, where $n$ may denote a phase, angle, or other parameter that alters the operator, and $P$ is often linked to the order of the fractional derivative. It delineates the extent of the fractional operation, where $0<P<1$ typically signifies a fractional derivative, with $P=1$ reverting to the conventional first-order derivative. The variable $t$ denotes the temporal variable in the examined system, $M$ generally indicates the truncation point or order, and $D$ represents the fractional derivative operator.

Here ${\text{H}}_{\text{n}}\left(.\right)$ is a truncated Mittag–Leffler function of one parameter that is defined by⁵³:

$${H}_{n}\left(z\right)=\sum_{j=0}^{i}\frac{{z}^{j}}{\Gamma \left(nj+1\right).}$$

Characteristics

Let $0<P<1, n>0, l,m\in \mathfrak{R}$ and $\Xi ,\Theta , P-$ differentiable at a point $\text{t}>0,$ then

• (1) ${D}_{M,t}^{P, n}\left(l\Xi \left(t\right)+m\Theta \left(t\right)\right)=l{D}_{M,t}^{P, n}\Xi \left(t\right)+m{D}_{M,t}^{P, n}\Theta \left(t\right)$,

• (2) ${D}_{M,t}^{P, n}\left(\Xi \left(t\right)\Theta \left(t\right)\right)=\Xi \left(t\right){D}_{M,t}^{P, n}\Theta \left(t\right)+\Theta \left(t\right){D}_{M,t}^{P, n}\Xi \left(t\right)$,

• (3) ${D}_{M,t}^{P, n}\left(\frac{\Xi \left(t\right)}{\Theta \left(t\right)}\right)=\frac{\Xi \left(t\right){D}_{M,t}^{P, n}\Theta \left(t\right)-\Theta \left(t\right){D}_{M,t}^{P, n}\Xi \left(t\right)}{{\Theta \left(t\right)}^{2}}$,

• (4) ${D}_{M,t}^{P, n}\left(\Xi \left(t\right)\right)=0,$ where $\Xi \left(t\right)=a$,

• (5) ${D}_{M,t}^{P, n}\Xi \left(t\right)=\frac{{t}^{1-P}}{\Gamma \left(n+1\right)}\frac{d\Xi \left(t\right)}{dt}$.

Methodology

To explain the procedure of the analytic soliton solution of PDEs, we considered a PDE in the subsequent form:

$$S\left(R, {R}_{x}, {R}_{t}, {{R}_{xx},R}_{tt}, {R}_{xt},\dots \right)=0,$$

(2)

where $R$ is a function of $x, t$ and $S$ is the function of $R$ and its derivatives,

$$R\left(x,t\right)={e}^{i\phi }R\left(\varphi \right), \varphi =kx-\omega t, \phi =kx-t\epsilon .$$

(3)

At first, we use the relation in Eq. (3) into Eq. (2) for convert Eq. (2) in ordinary form as:

$$T\left(R, {R}^{\prime}, {R}^{\prime\prime}, {R}^{\prime\prime\prime},\dots \right)=0.$$

(4)

Now, we will explore two significant techniques:

The new polynomial expansion (NPE) technique

According to the NPE technique, we set the trial solution of Eq. (4) as the following form^54,55:

$$u(\varphi )={\beta }_{0}+{\sum }_{l=1}^{n}\left({\beta }_{l}{\left(H(\varphi )\right)}^{l}+{\alpha }_{l}{\left(H(\varphi )\right)}^{-l}\right).$$

(5)

The number $n$ can be executed by balancing the highest derivative term with the nonlinear term as follows:

$${u}^{p}\frac{{d}^{m}u}{{d\varphi }^{m}}=pn+\left(n+m\right)$$

(6)

and $H(\varphi )$ satisfies the ODE in

$${H}^{\prime}(\varphi )={\theta }_{1}H\left(\varphi \right)+{\theta }_{2}{H\left(\varphi \right)}^{2}+{\theta }_{3.}$$

(7)

1. If ${\theta }_{1}$= 0, ${\theta }_{2}=1$, ${\theta }_{3}> 0$,

$$H\left(\varphi \right)=\sqrt{{\theta }_{3}} tan\left(\varphi \sqrt{{\theta }_{3}}\right),$$

$$H\left(\varphi \right)=-\sqrt{{\theta }_{3}} cot\left(\varphi \sqrt{{\theta }_{3}}\right).$$

2. If ${\theta }_{1}=0$, ${\theta }_{2}=1$, ${\theta }_{3}<0$,

$$H\left(\varphi \right)=-\sqrt{-{\theta }_{3}} tanh\left(\varphi \sqrt{-{\theta }_{3}}\right),$$

$$H\left(\varphi \right)=\sqrt{-{\theta }_{3}} coth\left(\varphi \sqrt{-{\theta }_{3}}\right).$$

3. If ${\theta }_{2}=1, {\theta }_{3}\ne 0$, ${\theta }_{1}\ne 0$,

$$H\left(\varphi \right)=\frac{{\beta }_{1}-{\beta }_{2}{S}_{1}{e}^{({\beta }_{1}-{\beta }_{2})\varphi }}{1-{S}_{1}{e}^{({\beta }_{1}-{\beta }_{2})\varphi }}.$$

Also ${S}_{1}$ is integrating constant, and ${\beta }_{1}$ and ${\beta }_{2}$ are the roots of ${{\theta }_{2}}^{2}+p{\theta }_{1}+q{\theta }_{3}$, i.e.,

$${\beta }_{1}=\frac{-p+\sqrt{{p}^{2}-4q}}{2}, {\beta }_{2}=\frac{-p-\sqrt{{p}^{2}-4q}}{2}.$$

4. If ${\theta }_{1}\ne 0, {\theta }_{2}\ne 0, {\theta }_{3}=0,$

$$H\left(\varphi \right)= =\frac{-{\text{l}}_{2}\delta }{{\text{l}}_{3}\left(\delta +cosh\left({\text{l}}_{2}\left(\varphi +\delta \right)\right)-sinh\left({\text{l}}_{2}\left(\varphi +\delta \right)-\right)\right)},$$

$$H\left(\varphi \right)= \frac{{\theta }_{1}exp\left({\theta }_{1}\left(\varphi +\delta \right)\right)}{1-{\theta }_{2}exp\left({\theta }_{1}\left(\varphi +\delta \right)\right)}; {\theta }_{1}>0, {\theta }_{2}< 0,$$

$$H\left(\varphi \right)=-\frac{{\text{l}}_{2}exp\left({\text{l}}_{2}\left(\varphi +\delta \right)\right)}{1+{\text{l}}_{3}exp\left({\text{l}}_{2}\left(\varphi +\delta \right)\right)}{\theta }_{1}<0, {\theta }_{2}> 0.$$

5. If ${\theta }_{2}=1,$ ${\theta }_{1}=0$, ${\theta }_{3}= 0$,

$$H\left(\varphi \right)=\frac{-1}{\varphi }.$$

6. If ${\theta }_{2}=1$; ${\theta }_{1}\ne 0$, ${\theta }_{3}=0$,

$$H\left(\varphi \right)=\frac{-{\theta }_{1}}{{S}_{0}{e}^{-{\theta }_{1}\varphi }-1},$$

${S}_{0}$ Represents the constant of integration.

Step 2: To consider the solutions, first, we find out the balance number $n$. Then we insert Eqs. (5) and (6) in Eq. (4).

Step 4: After inserting, we get a polynomial. If we equate the coefficient on both sides, then the system of equations is obtained. Now, we solve the system of equations for the arbitrary constant in the trial solution. If we insert the values of the arbitrary constant, then the required solutions are obtained.

Unified solver technique

In this subsection, we examine the unified solver technique^56,57,58 for solving ordinary differential equations:

$${{\wp }}_{1}{u}^{\prime\prime}+{{\wp }}_{2}{u}^{3}+{{\wp }}_{3}u=0.$$

(8)

Here ${\wp }_{1}, {\wp }_{2}, {\wp }_{3}$ are real numbers. The solutions are:

1. We get trigonometric solutions when the parametric conditions are ${\wp }_{3}=0$ and $\frac{{\wp }_{2}}{{\wp }_{1}}<0$,

$$u\left(\varphi \right)=\pm \sqrt{\frac{-{\wp }_{2}}{2{\wp }_{1}}}\frac{1}{\varphi }.$$

2. We get trigonometric solutions when the parametric conditions are $\frac{{\wp }_{3}}{{\wp }_{1}}<0$ and $\frac{{\wp }_{3}}{{\wp }_{2}}>0$,

$$u\left(\varphi \right)=\pm \sqrt{\frac{ {\wp }_{3}}{{\wp }_{2}}}tan\left(\sqrt{\frac{- {\wp }_{3}}{2{\wp }_{1}}}\varphi \right),$$

$$u\left(\varphi \right)=\pm \sqrt{\frac{\mathfrak{R}}{{\wp }_{2}}}cot\left(\sqrt{\frac{-\mathfrak{R}}{2{\wp }_{1}}}\varphi \right).$$

3. We get trigonometric solutions when the parametric conditions are $\frac{{\wp }_{3}}{{\wp }_{1}}>0$ and $\frac{{\wp }_{3}}{{\wp }_{2}}<0$,

$$u\left(\varphi \right)=\pm \sqrt{\frac{-{\wp }_{3}}{{\wp }_{2}}}tanh\left(\sqrt{\frac{{\wp }_{3}}{2{\wp }_{1}}}\varphi \right),$$

$$u\left(\varphi \right)=\pm \sqrt{-\frac{{\wp }_{3}}{{\wp }_{2}}}coth\left(\sqrt{\frac{{\wp }_{3}}{2{\wp }_{1}}}\varphi \right).$$

Mathematical analysis

The (2 + 1)-D chiral NLS model is considered as follows:

$$i{D}_{M,t}^{P, n}\text{G}+a\left({G}_{xx}+{G}_{zz}\right)+i\left\{{b}_{1}\left(G{G}_{x}^{*}-{G}^{*}{G}_{x}\right)\left.+{b}_{2}\left(G{G}_{z}^{*}-{G}^{*}{G}_{z}\right)\right\}G=0\right..$$

(9)

To solve Eq. (9), we assume that its soliton solution is expressed in the following form:

$$G(x,z,\tau )=\psi (\varphi ){\text{e}}^{i\phi },$$

(10)

Here, $\phi \left(x,z,t\right)={m}_{1}x+{m}_{2}z+\omega \frac{\Gamma \left(n+1\right)}{P}{t}^{P}+\theta$, and $\varphi (x,z,t)={A}_{1}x+{A}_{2}z-\delta \frac{\Gamma \left(n+1\right)}{P}{t}^{P}$.

After inserting Eq. (10) in Eq. (9), the real and imaginary parts appear. Now, we separate them as follows:

$$a\left({A}_{1}^{2}+{A}_{2}^{2}\right)\frac{{\text{d}}^{2}\psi }{\text{ d}{\varphi }^{2}}-\left(a\left({m}_{1}^{2}+{m}_{2}^{2}\right)+\omega \right)\psi +2\left({m}_{1}{b}_{1}+{m}_{2}{b}_{2}\right){\psi }^{3}=0,$$

(11)

$$\left(-\delta +2a\left({m}_{1}{A}_{1}+{m}_{2}{A}_{2}\right)\right)\frac{\text{d}\psi }{\text{ d}\varphi }=0.$$

(12)

From Eq. (12), we get

$$\delta =2a\left({m}_{1}{A}_{1}+{m}_{2}{A}_{2}\right).$$

Bifurcation analysis

In this section, we investigate the bifurcation analysis of (2 + 1)-D Chiral NLS model. The bifurcation analysis^59,60 is used in this paper to systematically investigate the qualitative changes in the system’s dynamic behaviour under varying parameters. Its purpose is to identify critical parameter values at which the nature of the solutions changes, such as the transition from periodic to chaotic behavior or the emergence of soliton-like structures. By performing bifurcation analysis, we can gain deeper insights into the stability, existence, and classification of different solution types, essential for understanding the underlying physical phenomena modeled by the equation.

Equation (11) can be written as:

$$\frac{{\text{d}}^{2}\psi }{\text{ d}{\varphi }^{2}}-\frac{\left(a\left({m}_{1}^{2}+{m}_{2}^{2}\right)+\omega \right)}{a\left({A}_{1}^{2}+{A}_{2}^{2}\right)}\psi +\frac{2\left({m}_{1}{b}_{1}+{m}_{2}{b}_{2}\right)}{a\left({A}_{1}^{2}+{A}_{2}^{2}\right)}{\psi }^{3}=0.$$

(13)

Now, we execute the transformation of Galilean into Eq. (13) as the following form:

$$\left\{\begin{array}{l}\frac{d\psi }{d\varphi }=L,\\ \frac{dL}{d\varphi }=-{\Xi }_{1}{\psi }^{3}+{\Xi }_{2}\psi \end{array},\right.$$

(14)

where, ${\Xi }_{1}=\frac{2\left({m}_{1}{b}_{1}+{m}_{2}{b}_{2}\right)}{a\left({A}_{1}^{2}+{A}_{2}^{2}\right)}, {\Xi }_{2}=\frac{\left(a\left({m}_{1}^{2}+{m}_{2}^{2}\right)+\omega \right)}{a\left({A}_{1}^{2}+{A}_{2}^{2}\right)}$,

$$\mathcal{H}(\psi , L)=\frac{{ L}^{2}}{2}+\frac{{\Xi }_{1}{\psi }^{4}}{4}-\frac{{\Xi }_{2}{\psi }^{2}}{2}=h$$

and $h$ is the constant of Hamiltonian. From Eq. (14), the succeeding equations are:

$$\left\{\begin{array}{l}L=0,\\ -{\Xi }_{1}{\psi }^{3}+{\Xi }_{2}\psi =0.\end{array}\right.$$

(15)

From Eq. (15), the equilibrium points are:

$${p}_{1}=(\text{0,0}), {p}_{2}=\left(\sqrt{\frac{{\Xi }_{2}}{{\Xi }_{1}}},0\right), {p}_{2}=\left(-\sqrt{\frac{{\Xi }_{2}}{{\Xi }_{1}}},0\right).$$

The determinant of Jacobian matrix for Eq. (15) is:

$$j(\psi , L)=\left|\begin{array}{ll}0&\quad 1\\ -{\Xi }_{1}{\psi }^{3}+{\Xi }_{2}\psi &\quad 0\end{array}\right|=-\left(-3{\Xi }_{1}{\psi }^{3}+{\Xi }_{2}\psi \right).$$

We know that:

• 1. If $j(\psi , L)<0$, then the saddle point is $(\psi , L)$,

• 2. If $j(\psi , L)>0$, then the center is $(\psi , L)$,

• 3. If $j(\psi , L)=0$, then the point of the cuspidor is $(\psi , L)$.

The results are recorded below:

Case 1: ${\Xi }_{1}>0$ and ${\Xi }_{2}>0$.

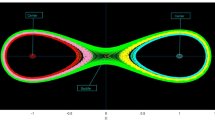
For ${\Xi }_{1}>0$ and ${\Xi }_{2}>0$, the system Eq. (14) has three equilibrium points. For $\text{a}=2, {m}_{1}=1, {b}_{1}=0.5, {m}_{2}=0.5, {b}_{2}=1, {A}_{1}=1, {A}_{2}=1$, $\upomega =-2$, we provide the phase portrait in Fig. 1a. The trajectories are not closed $\left(\text{0,0}\right)$, so this is a saddle and unstable point. The trajectories are closed at point $(-\text{1,0})$, and $(\text{1,0})$, so this works as a center and stable point.

Fig. 1

The phase portrait of the Eq. (14). (a) When ${\Xi }_{1}>0$, ${\Xi }_{2}>0$; (b) ${\Xi }_{1}<0$, ${\Xi }_{2}>0$; (c) ${\Xi }_{1}>0$, ${\Xi }_{2}<0$; (d) ${\Xi }_{1}<0$, ${\Xi }_{2}<0$.

Case 2: ${\Xi }_{1}<0$ and ${\Xi }_{2}>0$.

For ${\Xi }_{1}<0$ and ${\Xi }_{2}>0$, the system Eq. (14) has one equilibrium point. For $\text{a}=-2, {m}_{1}=1, {b}_{1}=1.5, {m}_{2}=1, {b}_{2}=1.5, {A}_{1}=1, {A}_{2}=1$, $\upomega =-8$, We provide the phase portrait in Fig. 1b. The trajectories are not closed at $\left(\text{0,0}\right)$, so this is a saddle and unstable point.

Case 3: ${\Xi }_{1}>0$ and ${\Xi }_{2}<0$.

For ${\Xi }_{1}>0$ and ${\Xi }_{2}<0$, the system Eq. (14) has one equilibrium point. For $\text{a}=-2, {m}_{1}=1, {b}_{1}=0.5, {m}_{2}=0.5, {b}_{2}=1, {A}_{1}=1, {A}_{2}=1$, $\upomega =2$, we provide the phase portrait in Fig. 1c. The trajectories are closed at $\left(\text{0,0}\right)$, so this point works as a center and stable point.

Case 4: ${\Xi }_{1}<0$ and ${\Xi }_{2}<0$.

For ${\Xi }_{1}>0$ and ${\Xi }_{2}>0$, The system Eq. (14) has three equilibrium points. For $\text{a}=-2, {m}_{1}=1, {b}_{1}=1.5, {m}_{2}=1, {b}_{2}=1.5, {A}_{1}=1, {A}_{2}=1$, $\upomega =10$, we provide the phase portrait in Fig. 1d. The trajectories are not closed $\left(\text{0,0}\right).$ Thus, this is a center and stable point. The trajectories are not closed at the points $(-\text{1,0})$, and $(\text{1,0})$, therefore, these points work as saddle and unstable points.

Analytic optical soliton solution

In this section, we apply two methods to solve the time M-fractional (2 + 1)-dimensional CNLSE equation.

The polynomial expansion technique

According to the technique, the solution of the Eq. (11) is:

$$\psi \left(\varphi \right)={\Xi }_{0}+{\Xi }_{1}H\left(\varphi \right)+\frac{{\mu }_{1}}{H\left(\varphi \right)}.$$

(16)

If we insert the Eq. (16) and its differential form in Eq. (6) into Eq. (11), then the following system of equations is obtained:

$$\left(2a{A}_{1}^{2}{\Xi }_{1}{\theta }_{2}^{2}+2a{A}_{2}^{2}{\Xi }_{1}{\theta }_{2}^{2}+2{\Xi }_{1}^{3}{b}_{1}{m}_{1}+2{\Xi }_{1}^{3}{b}_{2}{m}_{2}\right)=0,$$

$$\left(3a{A}_{1}^{2}{\Xi }_{1}{\theta }_{1}{\theta }_{2}+3a{A}_{2}^{2}{\Xi }_{1}{\theta }_{1}{\theta }_{2}\right.\left.+6{\Xi }_{0}{\Xi }_{1}^{2}{b}_{1}{m}_{1}+6{\Xi }_{0}{\Xi }_{1}^{2}{b}_{2}{m}_{2}\right)=0,$$

$$\begin{aligned}&\left(a{A}_{1}^{2}{\Xi }_{1}{\theta }_{1}^{2}+2a{A}_{1}^{2}{\Xi }_{1}{\theta }_{2}{\theta }_{3}+a{A}_{2}^{2}{\Xi }_{1}{\theta }_{1}^{2}+2a\right.{A}_{2}^{2}{\Xi }_{1}{\theta }_{2}{\theta }_{3} +6{\Xi }_{0}^{2}{\Xi }_{1}{b}_{1}{m}_{1}+6{\Xi }_{0}^{2}{\Xi }_{1}{b}_{2}{m}_{2}\\ &\quad+6{\Xi }_{1}^{2}{b}_{1}{m}_{1}{\mu }_{1}+6{\Xi }_{1}^{2}{b}_{2}{m}_{2}{\mu }_{1}+a{\Xi }_{1}{m}_{1}^{2}\left.+a{\Xi }_{1}{m}_{2}^{2}+a\omega {\Xi }_{1}\right)=0,\end{aligned}$$

$$\begin{aligned} &2a{\Xi }_{1}{\theta }_{1}{A}_{1}^{2}{\theta }_{3}+a{\mu }_{1}{\theta }_{1}{A}_{1}^{2}{\theta }_{2}+a{\Xi }_{1}{\theta }_{1}{A}_{2}^{2}{\theta }_{3}+a{\mu }_{1}{\theta }_{1}{A}_{2}^{2}{\theta }_{2}+2{\Xi }_{0}^{3}{m}_{1}{b}_{1}+2{\Xi }_{0}^{3}{m}_{2}{b}_{2}\\ &\quad+12{\Xi }_{0}{\Xi }_{1}{\mu }_{1}{m}_{1}{b}_{1}+12{\Xi }_{0}{\Xi }_{1}{\mu }_{1}{m}_{2}{b}_{2}+a{\Xi }_{0}{m}_{1}^{2}+a{\Xi }_{0}{m}_{2}^{2}+a{\Xi }_{0}\omega =0.\end{aligned}$$

$$\begin{aligned}& a{A}_{1}^{2}{\mu }_{1}{\theta }_{1}^{2}+2a{A}_{1}^{2}{\mu }_{1}{\theta }_{2}{\theta }_{3}+a{A}_{2}^{2}{\mu }_{1}{\theta }_{1}^{2}+2a{A}_{2}^{2}{\mu }_{1}{\theta }_{2}{\theta }_{3}+6{\Xi }_{0}^{2}{b}_{1}{m}_{1}{\mu }_{1}+6{\Xi }_{0}^{2}{b}_{2}{m}_{2}{\mu }_{1}\\ &\quad+6{\Xi }_{1}{b}_{1}{m}_{1}{\mu }_{1}^{2}+6{\Xi }_{1}{b}_{2}{m}_{2}{\mu }_{1}^{2}+a{m}_{1}^{2}{\mu }_{1}+a{m}_{2}^{2}{\mu }_{1}+a0{\mu }_{1}=0,\end{aligned}$$

$$3a{A}_{1}^{2}{\mu }_{1}{\theta }_{1}{\theta }_{3}+3a{A}_{2}^{2}{\mu }_{1}{\theta }_{1}{\theta }_{3}+6{\Xi }_{0}{b}_{1}{m}_{1}{\mu }_{1}^{2}+6{\Xi }_{0}{b}_{2}{m}_{2}{\mu }_{1}^{2}=0,$$

$$2a{A}_{1}^{2}{\mu }_{1}{\theta }_{3}^{2}+2a{A}_{2}^{2}{\mu }_{1}{\theta }_{3}^{2}+2{b}_{1}{m}_{1}{\mu }_{1}^{3}+2{b}_{2}{m}_{2}{\mu }_{1}^{3}=0.$$

By solving the resulting system of equations using Maple, we obtain three sets of solutions:

Case 1:

$$\begin{aligned}\omega &=-\frac{1}{4}\frac{1}{{b}_{1}^{2}{\mu }_{1}^{4}}\left({a}^{2}{A}_{1}^{4}{\theta }_{3}^{4}-{A}_{1}^{2}{b}_{1}^{2}{\mu }_{1}^{4}{\theta }_{1}^{2}-8{A}_{1}^{2}{b}_{1}^{2}{\mu }_{1}^{4}{\theta }_{2}{\theta }_{3}+4a{A}_{1}^{2}{\hslash }_{2}{m}_{2}{\mu }_{1}^{2}{\theta }_{3}^{2}+4{b}_{1}^{2}{\mu }_{2}^{2}{\mu }_{1}^{4}\right.\left.+4{b}_{2}^{2}{m}_{2}^{2}{\mu }_{1}^{4}\right),\\ {A}_{2}&=\frac{\text{I}{A}_{1}}{2},{\Xi }_{0}-\frac{1}{2}\frac{{\mu }_{1}{\theta }_{1}}{{\theta }_{3}},{\Xi }_{1}=\frac{{\mu }_{1}{\theta }_{2}}{{\theta }_{3}},{m}_{1}=-\frac{1}{2}\frac{u{A}_{1}^{2}{\theta }_{3}^{2}+2{b}_{2}{m}_{2}{\mu }_{1}^{2}}{{b}_{1}{\mu }_{1}^{2}} \end{aligned}$$

.

If ${\theta }_{1}$= 0, ${\theta }_{2}=1$, ${\theta }_{3}< 0$,

$$G\left(x,z,t\right)=-\left(\frac{{\mu }_{1}{\theta }_{2}}{{\theta }_{3}}\sqrt{-{\theta }_{3}} tanh\left(\varphi \sqrt{-{\theta }_{3}}\right)+\frac{{\mu }_{1}}{\sqrt{-{\theta }_{3}} tanh\left(\varphi \sqrt{-{\theta }_{3}}\right)}\right){\text{e}}^{i\phi },$$

(17)

$$G\left(x,z,t\right)=\left(\frac{{\mu }_{1}{\theta }_{2}}{{\theta }_{3}}\sqrt{-{\theta }_{3}} coth\left(\varphi \sqrt{-{\theta }_{3}}\right)+\frac{{\mu }_{1}}{\sqrt{-{\theta }_{3}} tanh\left(\varphi \sqrt{-{\theta }_{3}}\right)}\right){\text{e}}^{i\phi }.$$

(18)

If ${\theta }_{1}=0$, ${\theta }_{2}=1$, ${\theta }_{3}>0$,

$$G\left(x,z,t\right)=\left(\frac{{\mu }_{1}{\theta }_{2}}{{\theta }_{3}}\sqrt{{\theta }_{3}} tan\left(\varphi \sqrt{{\theta }_{3}}\right)+\frac{{\mu }_{1}}{\sqrt{{\theta }_{3}} tan\left(\varphi \sqrt{{\theta }_{3}}\right)}\right){\text{e}}^{i\phi },$$

(19)

$$G\left(x,z,t\right)=-\left(\frac{{\mu }_{1}{\theta }_{2}}{{\theta }_{3}}\sqrt{{\theta }_{3}} cot\left(\varphi \sqrt{{\theta }_{3}}\right)+\frac{{\mu }_{1}}{\sqrt{{\theta }_{3}} cot\left(\varphi \sqrt{{\theta }_{3}}\right)}\right){\text{e}}^{i\phi }.$$

(20)

If ${\theta }_{2}=1, {\theta }_{3}\ne 0$, ${\theta }_{1}\ne 0$,

$$G\left(x,z,t\right)=\left(\frac{{\mu }_{1}{\theta }_{2}}{{\theta }_{3}}\frac{{\beta }_{1}-{\beta }_{2}{S}_{1}{e}^{({\beta }_{1}-{\beta }_{2})\varphi }}{1-{S}_{1}{e}^{({\beta }_{1}-{\beta }_{2})\varphi }}+\frac{{\mu }_{1}}{\frac{{\beta }_{1}-{\beta }_{2}{S}_{1}{e}^{({\beta }_{1}-{\beta }_{2})\varphi }}{1-{S}_{1}{e}^{({\beta }_{1}-{\beta }_{2})\varphi }}}\right){\text{e}}^{i\phi },$$

(21)

Where ${S}_{1}$ is integrating constant, and ${\beta }_{1}$ and ${\beta }_{2}$ are the roots of ${{\theta }_{2}}^{2}+p{\theta }_{1}+q{\theta }_{3}$, i.e.,

$${\beta }_{1}=\frac{-p+\sqrt{{p}^{2}-4q}}{2}, {\beta }_{2}=\frac{-p-\sqrt{{p}^{2}-4q}}{2}.$$

If ${\theta }_{3}=0,$ then all solutions are rejected.

Here, $\phi \left(x,z,t\right)={m}_{1}x+{m}_{2}z+\omega \frac{\Gamma \left(n+1\right)}{P}{t}^{P}+\theta$, and $\varphi (x,z,t)={A}_{1}x+{A}_{2}z-\delta \frac{\Gamma \left(n+1\right)}{P}{t}^{P}$.

Case 2: ${A}_{2}=\text{I}{A}_{1},{\Xi }_{0}={\Xi }_{0},{\Xi }_{1}=0,{m}_{1}=-{b}_{2}\sqrt{\frac{-\omega }{\left({b}_{1}^{2}+{b}_{2}^{2}\right)}},{m}_{2}={b}_{1}\sqrt{\frac{-\omega }{\left({b}_{1}^{2}+{b}_{2}^{2}\right)}},{\mu }_{1}={\mu }_{1}$.

If ${\theta }_{1}$= 0, ${\theta }_{2}=1$, ${\theta }_{3}> 0$,

$$G\left(x,z,t\right)=\left(\frac{{\mu }_{1}}{\sqrt{{\theta }_{3}} tan\left(\varphi \sqrt{{\theta }_{3}}\right)}\right){\text{e}}^{i\phi },$$

(22)

$$G\left(x,z,t\right)=-\left(\frac{{\mu }_{1}}{\sqrt{{\theta }_{3}} cot\left(\varphi \sqrt{{\theta }_{3}}\right)}\right){\text{e}}^{i\phi }.$$

(23)

If ${\theta }_{1}=0$, ${\theta }_{2}=1$, ${\theta }_{3}<0$,

$$G\left(x,z,t\right)=-\left(\frac{{\mu }_{1}}{\sqrt{-{\theta }_{3}} tanh\left(\varphi \sqrt{-{\theta }_{3}}\right)}\right){\text{e}}^{i\phi },$$

(24)

$$G\left(x,z,t\right)=\left(\frac{{\mu }_{1}}{\sqrt{-{\theta }_{3}} tanh\left(\varphi \sqrt{-{\theta }_{3}}\right)}\right){\text{e}}^{i\phi }.$$

(25)

If ${\theta }_{2}=1, {\theta }_{3}\ne 0$, ${\theta }_{1}\ne 0$,

$$G\left(x,z,t\right)=\left(\frac{{\mu }_{1}}{\frac{{\beta }_{1}-{\beta }_{2}{S}_{1}{e}^{({\beta }_{1}-{\beta }_{2})\varphi }}{1-{S}_{1}{e}^{({\beta }_{1}-{\beta }_{2})\varphi }}}\right){\text{e}}^{i\phi },$$

(26)

where ${S}_{1}$ is integrating constant, and ${\beta }_{1}$ and ${\beta }_{2}$ are the roots of ${{\theta }_{2}}^{2}+p{\theta }_{1}+q{\theta }_{3}$, i.e.,

$${\beta }_{1}=\frac{-p+\sqrt{{p}^{2}-4q}}{2}, {\beta }_{2}=\frac{-p-\sqrt{{p}^{2}-4q}}{2}.$$

If ${\theta }_{1}\ne 0, {\theta }_{2}\ne 0, {\theta }_{3}=0,$

$$G\left(x,z,t\right)=\left(\frac{{\mu }_{1}}{\frac{-{\theta }_{1}\delta }{{\theta }_{3}\left(\delta +cosh\left({\theta }_{1}\left(\varphi +\delta \right)\right)-sinh\left({\theta }_{1}\left(\varphi +\delta \right)-\right)\right)}}\right){\text{e}}^{i\phi },$$

(27)

$$G\left(x,z,t\right)=\left(\frac{{\mu }_{1}}{\frac{{\theta }_{1}exp\left({\theta }_{1}\left(\varphi +\delta \right)\right)}{1-{\theta }_{2}exp\left({\theta }_{1}\left(\varphi +\delta \right)\right)}}\right){\text{e}}^{i\phi };{\theta }_{1}>0, {\theta }_{2}< 0,$$

(28)

$$G\left(x,z,t\right)=\left(\frac{-{\mu }_{1}}{\frac{{\text{l}}_{2}exp\left({\text{l}}_{2}\left(\varphi +\delta \right)\right)}{1+{\text{l}}_{3}exp\left({\text{l}}_{2}\left(\varphi +\delta \right)\right)}}\right){\text{e}}^{i\phi };{\theta }_{1}<0, {\theta }_{2}> 0.$$

(29)

If ${\theta }_{2}=1,$ ${\theta }_{1}=0$, ${\theta }_{3}= 0$,

$$G\left(x,z,t\right)={\mu }_{1}\varphi {\text{e}}^{i\phi }.$$

(30)

If ${\theta }_{2}=1$; ${\theta }_{1}\ne 0$, ${\theta }_{3}=0$,

$$G\left(x,z,t\right)=\left(\frac{-{\mu }_{1}}{\frac{{\theta }_{1}}{{S}_{0}{e}^{-{\theta }_{1}\varphi }-1}}\right){\text{e}}^{i\phi };{\theta }_{1}<0, {\theta }_{2}> 0,$$

(31)

where ${S}_{0}$ represents the constant of integration.

Here, $\phi \left(x,z,t\right)=-{b}_{2}\sqrt{\frac{-\omega }{\left({b}_{1}^{2}+{b}_{2}^{2}\right)}}x+{b}_{1}\sqrt{\frac{-\omega }{\left({b}_{1}^{2}+{b}_{2}^{2}\right)}}z+\omega \frac{\Gamma \left(n+1\right)}{P}{t}^{P}+\theta,$ and $\varphi (x,z,t)={A}_{1}x+\text{I}{A}_{1}z-\delta \frac{\Gamma \left(n+1\right)}{P}{t}^{P}.$

Unified solver technique

In this subsection, we employ the unified solver technique to analyze the (2 + 1)-dimensional CNSE, which is expressed in the following standard form:

$$a\left({A}_{1}^{2}+{A}_{2}^{2}\right)\frac{{\text{d}}^{2}\psi }{\text{ d}{\varphi }^{2}}-\left(a\left({m}_{1}^{2}+{m}_{2}^{2}\right)+\omega \right)\psi +2\left({m}_{1}{b}_{1}+{m}_{2}{b}_{2}\right){\psi }^{3}=0.$$

(32)

1. We get rational solutions when the parametric conditions are $\left(a\left({m}_{1}^{2}+{m}_{2}^{2}\right)+\omega \right) =0$ and $\frac{2\left({m}_{1}{b}_{1}+{m}_{2}{b}_{2}\right)}{a\left({A}_{1}^{2}+{A}_{2}^{2}\right)}<0$.

$$G\left(x,z,t\right)=\left(\sqrt{\frac{-2\left({m}_{1}{b}_{1}+{m}_{2}{b}_{2}\right)}{2a\left({A}_{1}^{2}+{A}_{2}^{2}\right)}}\frac{1}{\varphi }\right){\text{e}}^{i\phi },$$

(33)

2. We get trigonometric solutions when the parametric conditions are $\frac{-\left(a\left({m}_{1}^{2}+{m}_{2}^{2}\right)+\omega \right) }{a\left({A}_{1}^{2}+{A}_{2}^{2}\right)}<0$ and $\frac{-\left(a\left({m}_{1}^{2}+{m}_{2}^{2}\right)+\omega \right)}{2\left({m}_{1}{b}_{1}+{m}_{2}{b}_{2}\right)}>0$.

$$G\left(x,z,t\right)=\left(\sqrt{\frac{ -\left(a\left({m}_{1}^{2}+{m}_{2}^{2}\right)+\omega \right)}{2\left({m}_{1}{b}_{1}+{m}_{2}{b}_{2}\right)}}tan\left(\sqrt{\frac{\left(a\left({m}_{1}^{2}+{m}_{2}^{2}\right)+\omega \right) }{2a\left({A}_{1}^{2}+{A}_{2}^{2}\right) }}\varphi \right)\right){\text{e}}^{i\phi },$$

(34)

$$G\left(x,z,t\right)=\left(\sqrt{\frac{-\left(a\left({m}_{1}^{2}+{m}_{2}^{2}\right)+\omega \right) }{2\left({m}_{1}{b}_{1}+{m}_{2}{b}_{2}\right)}}cot\left(\sqrt{\frac{\left(a\left({m}_{1}^{2}+{m}_{2}^{2}\right)+\omega \right)}{2a\left({A}_{1}^{2}+{A}_{2}^{2}\right)}}\varphi \right)\right){\text{e}}^{i\phi },$$

(35)

3. We get trigonometric solutions when the parametric conditions are $\frac{-\left(a\left({m}_{1}^{2}+{m}_{2}^{2}\right)+\omega \right)}{a\left({A}_{1}^{2}+{A}_{2}^{2}\right)}>0$ and $\frac{-\left(a\left({m}_{1}^{2}+{m}_{2}^{2}\right)+\omega \right)}{2\left({m}_{1}{b}_{1}+{m}_{2}{b}_{2}\right)}<0$.

$$G\left(x,z,t\right)=\left(\sqrt{\frac{\left(a\left({m}_{1}^{2}+{m}_{2}^{2}\right)+\omega \right)}{2\left({m}_{1}{b}_{1}+{m}_{2}{b}_{2}\right)}}tanh\left(\sqrt{\frac{-\left(a\left({m}_{1}^{2}+{m}_{2}^{2}\right)+\omega \right)}{2a\left({A}_{1}^{2}+{A}_{2}^{2}\right)}}\varphi \right)\right){\text{e}}^{i\phi },$$

(36)

$$G\left(x,z,t\right)=\left(\sqrt{\frac{\left(a\left({m}_{1}^{2}+{m}_{2}^{2}\right)+\omega \right)}{2\left({m}_{1}{b}_{1}+{m}_{2}{b}_{2}\right)}}coth\left(\sqrt{\frac{-\left(a\left({m}_{1}^{2}+{m}_{2}^{2}\right)+\omega \right) }{2a\left({A}_{1}^{2}+{A}_{2}^{2}\right)}}\varphi \right) \right){\text{e}}^{i\phi },$$

(37)

Here, $\phi \left(x,z,t\right)={m}_{1}x+{m}_{2}z+\omega \frac{\Gamma \left(n+1\right)}{P}{t}^{P}+\theta$, and $\varphi (x,z,t)={A}_{1}x+{A}_{2}z-\delta \frac{\Gamma \left(n+1\right)}{P}{t}^{P}$.

Figure analysis

Recently, the study of optical soliton solutions in fiber optic communication systems has gained significance. Throughout the last two decades, there has been much research investigating optical solitons from diverse existing models. In addition, an important development of this century is the use of fiber amplifiers, optical solitons, and nonlinear processes in optical fiber for long-distance data transmission, even underwater. The increasing need for communication networks with high performance, large capacity, and ultra-wideband capabilities has spurred the creation of new technologies and given scientists new tasks to complete. Thus, it is essential to investigate the mathematical characteristics of soliton pulses. One will gain a greater comprehension of the engineering aspects associated with these solutions by doing this. In this study, various soliton structures, including bright periodic solitons, kink periodic solitons, dark periodic solitons, kinky-periodic solitons, anti-kink bright solitons, and interactions between kink and dark solitons, display unique characteristics that affect signal transmission efficiency and stability. Bright periodic solitons are crucial in optical fibers as they preserve their form while traversing a nonlinear medium. These solitons facilitate effective data transfer by mitigating dispersion effects, thereby enabling high-speed communication with little signal distortion. Dark periodic solitons, defined by localized intensity minima, are essential in optical fiber systems as they enable reliable transmission in defocusing environments. They are especially beneficial in wavelength-division multiplexing (WDM) systems, where they improve signal integrity and reduce cross-talk. Kinky-periodic solitons display a synthesis of kink-like and periodic characteristics, enhancing the resilience of optical signal transmission. Their distinctive characteristics enable the creation of stable, self-sustaining wave patterns, which can be utilized in optical logic gates and nonlinear signal processing applications. The coexistence of anti-kink and brilliant solitons improves optical communication efficacy by facilitating energy redistribution across the signal waveform. This interaction can be utilized for optical pulse shaping, resulting in enhanced signal quality in long-distance communication networks. The interplay between kink and dark solitons is especially pertinent in the development of all-optical signal processing systems. These soliton structures can be employed to create optical diodes, signal regeneration systems, and high-speed optical computer frameworks. The various soliton phenomena mentioned above are essential for the advancement of optical communication technology. Their capacity to sustain stability, regulate dispersion, and facilitate nonlinear signal processing renders them indispensable in contemporary communications networks.

The polynomial expansion technique

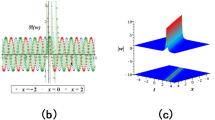
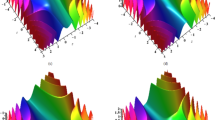
In this subsection, we analyze the numerical structure and dynamic characteristics of the solutions obtained for the (2 + 1)-dimensional CNSE model using the polynomial expansion technique. This approach allows for the exploration of various optical wave patterns, as illustrated in Figs. 2, 3, 4, 5, 6, including different forms of chaotic periodic waves, double-periodic waves, and periodic rogue wave patterns. The derived solitons propagate within a nonlinear dispersive fiber. Figure 2 demonstrates the anti-kink with bright soliton of Eq. (17) for the values $z={\theta }_{1}=1,{b}_{1}=0.2,a=0.5,{A}_{2}=-0.01, {m}_{1}=0.5,{\theta }_{2}=0,{m}_{2}=0.1,{b}_{2}=-0.1,{\mu }_{1}=1,\Omega =-0.01, n=1.5,{\theta }_{3}=-0.2$. In the 2D diagram, we present the impact of the fractional parameter along with x-axis and t-axis, respectively. Figure 3 illustrates the interaction of kink and dark soliton from Eq. (18) for the ideals $z={\theta }_{2}=1,{\theta }_{1}=0,{\theta }_{3}=-0.5,{b}_{1}=0.5,{b}_{2}=1.5,a=-0.5,{A}_{2}=1, {m}_{1}=-0.2,{m}_{2}=0.5,{\mu }_{1}=-0.5,\Omega =-0.1,n=1.5$. Figure 4, displays bright periodic soliton of the Eq. (19) for ideals $z={\theta }_{2}=1,{\theta }_{1}=0,{\theta }_{3}=1,{\mu }_{1}=0.5,{b}_{1}=-0.5,{b}_{2}=1.5,a=-0.5,{A}_{2}=1, {m}_{1}=-0.2,{m}_{2}=0.5,\Omega =-0.1,n=1.5$. In 2D diagram, the amplitude of the optical pulse is gradually decreased with the increased fractional parameter. Figure 5, exhibitions two-sided kink soliton of the Eq. (22) for ideals $z={\theta }_{2}=1,{\theta }_{1}=0,{\theta }_{3}=0.1,{\mu }_{1}=0.5,{b}_{1}=-4,{b}_{2}=1,a=0.5,{A}_{2}=0.5,{\Xi }_{0}=1, \omega =0.5,\Omega =0.1,n=1.5$. In 2D diagram, the amplitude of the optical pulse is gradually decreased with the increased fractional parameter. Figure 6 displays the 3D with density and 2D view of the solution Eq. (24) which is the kinky-periodic soliton for the parametric values $z={\theta }_{2}=1,{\theta }_{1}=0,{\theta }_{3}=1,{\mu }_{1}=0.5,{b}_{1}=1,{b}_{2}=0.5,a=0.5,{A}_{2}=-1,{\Xi }_{0}=1, \omega =-1,\Omega =0.1,n=1.5$.

Fig. 2

Visualize the optical wave view of Eq. (17).

Fig. 3

Visualize the optical wave view of Eq. (18).

Fig. 4

Visualize the optical wave view of Eq. (19).

Fig. 5

Visualize the optical wave view of Eq. (22).

Fig. 6

Visualize the optical wave view of Eq. (24).

Unified solver technique

In this subsection, we examine the numerical structure and the dynamic properties of the solutions derived for the (2 + 1) CNSE model using the Unified Solver technique. This method is applied to investigate various optical wave patterns, as shown in Figs. 7, 8, 9, including different forms of chaotic periodic breather waves, periodic waves, double periodic wave, and periodic breather waves with bright-type periodic soliton. The resulting solitons propagate through a nonlinear dispersive fiber. Figure 7 demonstrates the dark singular soliton of Eq. (34) for the ideals $z=1,{b}_{2}=1,{m}_{1}={m}_{2}=1,{b}_{1}=1,{A}_{1}=1,{A}_{2}=2,{\Xi }_{0}=1, \omega =-0.1,\Omega =-0.1,a=-0.5,n=1.5$. In 2D diagram, the periodicity increased and amplitude decreased with increasing the value of the fractional parameter. Figure 8 demonstrates kink with periodic wave of Eq. (36) for the ideals $z=1,{b}_{1}=0.1,{b}_{2}=-1.5,a=-0.5,{m}_{1}={m}_{2}=-1,{A}_{1}=-1,{A}_{2}=-2,{\Xi }_{0}=1, \omega =-13,\Omega =-0.1,n=1.5$. The influence of the truncated M-fractional parameters is illustrated through 2D plots, with the $x$-axis and $t$-axis representing the respective variables. In 2D diagram, the periodicity and amplitude are constant with increasing the value of the fractional parameter. Figure 9, displays anti-kink with periodic wave of Eq. (37) for ideals $z=1,{b}_{1}={b}_{2}=1,a=-0.5,{m}_{1}={m}_{2}=1,{A}_{1}=1,{A}_{2}=2, \omega =-0.1,\Omega =-0.1,n=1.5$. The influence of the truncated M-fractional parameters is illustrated through 3D with density and 2D plots along with the $x$-axis and $t$-axis representing the respective variables.

Fig. 7

Visualize the optical wave view of Eq. (34).

Fig. 8

Visualize the optical wave view of Eq. (36).

Fig. 9

Visualize the optical wave view of Eq. (37).

Comparison and novelty

In this section, we compare our results with those presented in high-quality studies referenced in^30,31,39.

Comparison

Ghanbari et al.³⁰ explored the fractional (2 + 1)-dimensional CNLSE using the generalized exponential rational function method, deriving novel soliton, periodic wave, and kink-type solutions exhibiting intricate structures. Raza et al.³¹ employed the extended direct algebraic method and the extended trial equation approach to analyze the (2 + 1)-dimensional CNLSE, obtaining bright soliton, dark soliton, and dark singular soliton solutions. Bulut et al.³⁹ utilized the sine–Gordon expansion method to examine the (1 + 1)-and (2 + 1)-dimensional CNLSE, identifying dark and bright soliton solutions.

Novelty

In this study, we employed polynomial expansion (NPE) and unified solver techniques to develop optical soliton solutions. Under specific parametric conditions, the derived solutions are articulated as rational, exponential, trigonometric, and hyperbolic function solutions. The numerical solutions produced include the bright periodic soliton, anti-kink with bright soliton, interaction of kink and dark soliton, kink and anti-kink with periodic soliton, dark periodic soliton, and kinky-periodic soliton solutions. This study examines the relationship between kink and dark solitons, as well as between kink and anti-kink with periodic solitons, dark periodic solitons, and kinky-periodic soliton solutions for the first time. Furthermore, we introduce the bifurcation analysis of the proposed model. The phase portrait is utilized to examine stable and unstable solutions. Furthermore, we examine the modulation instability of the suggested model. We also demonstrate the impact of the M-fractional derivative on the derived solutions for various orders of the fractional derivative for $P=0.1, 0.5,$ and $0.9$.

Advantages and limitations of the proposed methods

In this section, we present the advantages and limitations of the modified simple equation method for solving NLEEs.

Advantages of the polynomial expansion (NPE) and unified solver techniques

• Can be applied to different classes of nonlinear PDEs, including integrable and non-integrable systems.

• Unlike purely numerical approaches, these methods provide explicit solutions, aiding theoretical insights.

• The unified solver technique reduces the need for multiple separate methods, offering a streamlined way to obtain diverse solutions.

• The unified solver technique provides a framework that accommodates multiple types of solutions (e.g., rational, hyperbolic, and trigonometric solutions) under a single approach.

• The polynomial expansion method (e.g., the modified F-expansion method) allows for the systematic construction of exact analytical solutions, including periodic and soliton-like solutions.

Limitations of the polynomial expansion (NPE) and unified solver techniques

The limitations of the MSE Method are:

• These methods are most effective for integrable or near-integrable systems.

• If the equation lacks the Painlevé property or does not admit polynomial-based solutions, modifications are needed.

• As the degree of the polynomial increases, the algebraic system becomes more complicated, making solution extraction challenging.

• The unified solver method applies to all types of NLPDEs that have the ODE form in ${\wp }_{1}{u}^{{\prime}{\prime}}+{\wp }_{2}{u}^{3}+{\wp }_{3}u=0$.

Conclusion

The M-fraction chiral (2 + 1) dimensional NSE has been successfully studied in this framework by helping the bifurcation analysis and two effective techniques namely polynomial expansion (PE) technique and the unified solver technique. At first, the bifurcation analysis within the framework for the chiral (2 + 1) dimensional NSE is essential for comprehending the transition between stable and unstable soliton solutions. This signifies a pivotal juncture where two solution branches converge, resulting in the creation or destruction of single waves. This bifurcation offers critical insights into the stability and dynamics of wave propagation in nonlinear media, including optical fibers and plasma systems. Secondly, we applied the PE and US techniques to find the analytic solutions in the form of optical pulses as well as hyperbolic, rational, exponential, and periodic solutions. Under the different conditions, the obtained solutions by using the PE technique provided some complex phenomena including bright periodic soliton, anti-kink with bright soliton, interaction of kink and dark soliton solutions by unified solver technique provided kink and anti-kink with periodic soliton, dark periodic soliton, and kinky-periodic soliton solutions are obtained. In nonlinear optical fiber, the achieved optical soliton solutions in this study have physical significance. Compared to an ordinary soliton, this soliton exhibits a higher degree of manipulation complexity; however, it offers improved stability and flexibility when dealing with losses. By varying the values of the free parameters, the movement of the resultant solution is recorded as density plots, 2D plots, and 3D plots, as shown in Figs. 2, 3, 4, 5, 6, 7, 8, 9. In future research, we will investigate the chaotic nature^61,62, multi-stability, Poincare, layponov, and sensitivity analysis for the proposed model. It is anticipated that the acquired solutions will be essential to comprehending the fundamental physical concepts of evolutionary processes.