Simulation-based review of classical, heuristic, and metaheuristic path planning algorithms

Abstract

Path planning is the process by which an autonomous robot obtains information about its environment and chooses the best route from the start point to the target destination while avoiding obstacles. It is vital to the success of robot operation as it provides autonomous maneuverability within the environment, ensuring a collision-free and optimum path that guarantees efficient movement. This paper introduces and categorizes several notable path-planning algorithms used in robotics operations. We delve into their basic principles, key features, challenges, and real-world applications. Additionally, we provided a simulated comparison result of the notable path-planning algorithms. Finally, we analyze the outcomes, give a concise conclusion, and forecast the future trends in path planning techniques.

Introduction

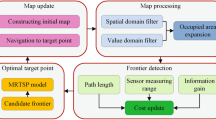
The importance of path planning in robotics and autonomous control has drawn the interest of researchers in recent years. Path planning aims to establish a collision-free and optimum path that guides a mobile robot from a start position to a target point¹. Different path planning algorithms exist with their inherent obstacle avoidance technique that guides the robot around an obstacle to avoid collision. Many obstacle avoidance techniques suit various situations, tasks, and environments. Still, they also come with limitations such as performance issues, increased path length, memory consumption, computational cost, and sometimes inability to reach goals. The primary aim of most of the notable path planning algorithms and techniques in robotics is to generate an optimal, collision-free path that is reliable, feasible, and computationally efficient^2,3,4 as depicted in Fig. 1. Path planning is a significant huddle in deploying mobile robots as it lays the foundation and directs solutions to other associated challenges in robotic navigation. The intricacy of path planning increases with the dimension and the number of obstacles in configuration area⁴, which influences the choice of the most appropriate planning technique.

Fig. 1

Robotic domain shows clearance around an obstacle and path length.

Adopting a path-planning technique requires a thorough assessment, understanding, mapping, and tracking of the robot’s position in its configuration area, as shown in Fig. 2.

Fig. 2

Robotic path planning processes from Start position to Goal position.

Contribution and organization of the paper

The significant contributions of this paper are as follows

• The paper introduces and classifies notable path-planning algorithms used in robotics.

• It highlights the basic principles, fundamental features, challenges, and real-life applications of conventional path-planning techniques.

• It provides simulated comparison and analysis of the results of selected conventional (Classical and Heuristic) path planning algorithms.

Finally, the paper projected the future outlook of path-planning techniques in robotics.

Path planning techniques and classifications

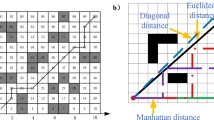
Researchers have categorized path-planning techniques based on adopted methodologies and other criteria. The various classifications of Path-planning techniques are Global or Local path planning based on the data received from the environment, offline (static path) planning, Online (dynamic path) planning based on the characteristics of the obstacles in the environment, and classic, Heuristic, and Metaheuristic planning based on the computational need⁴, as shown in Fig. 3.

Fig. 3

Path planning classification.

Classical approach

The Classical approaches to path planning can be broadly classified into search-based and sample-based methods. The search-based methods are classical approaches to path planning that systematically explore the search space to find an optimal or feasible path from a start point to a goal point. These methods are based on graph search algorithms. They include Breadth-First Search (BFS), Depth-First Search (DFS), Dijkstra’s Algorithm, Greedy Best-First Search, Bellman-Ford Algorithm, Iterative Deepening Search (IDS). The Sample-based methods are a class of path planning algorithms that rely on randomly sampling the configuration space to find feasible paths from a start to a goal point. These methods are particularly useful in high-dimensional spaces where traditional search-based methods may be inefficient. The sample-based methods include Probabilistic Roadmap (PRM), Rapidly-exploring Random Tree (RRT), RRT-Connect, RRT*, Expansive Space Trees (EST), and Lazy PRM^4,5,6,7. Some of the limitations of classical approaches is their high computational demand, inability to cope with unpredictability and challenges in dealing with large data from a wide environment.

Dijkstra algorithm

Edsger Wybe Dijkstra introduced Dijkstra’s algorithm in 1959. The algorithm applies a graph-based technique that uses a grid and lattice to map the environment as a graph, with nodes representing discrete positions or states in the environment while edges represent feasible transitions between nodes. This technique tends to be slow when applied to problem areas with high-dimensional spaces, such as robotic manipulators with many degrees of freedom^8,9,10. Figure 4 shows the path generated for a mobile robot using Dijkstra’s algorithm, illustrating its effectiveness in finding the shortest route.

Fig. 4

Robot path generated with Dijkstra’s algorithm.

Dijkstra’s algorithm effectively solves problems that require finding the shortest path from a start point to a destination within a graph. It has proven effective in problems that require finding the shortest possible path within a web of interconnected nodes. Such a problem is sometimes called the single-source shortest paths problem^11,12. It picks an unvisited vertex with the lowest distance, calculates the distance through it to other unvisited neighbors, and updates the neighbor’s distance if it is smaller than the previous distance. The traditional Dijkstra algorithm uses the breadth-first search strategy. It starts from the specified node and iteratively goes through all other nodes by weights to finally obtain the optimal path tree from the start to the goal nodes. The algorithm’s running time is O(n²)¹³. Equation 1 shows the Dijkstra’s algorithm function.

$${\varvec{f}}\left( {\varvec{n}} \right) = {\varvec{g}}\left( {\varvec{n}} \right)$$

(1)

where g(n) is the path cost from the start node to node n.

Dijkstra’s algorithm is one of the most classical and mature algorithms for searching the shortest path in the graph. However, the major drawback of this algorithm is that it has high time computation complexity, is computationally intensive, has low efficiency, weak obstacle avoidance, takes up larger storage space, and is less effective if the distance between the starting location and the destination is far from each other^13,14,15. Experts and scholars have conducted a reasonable amount of research and studies to overcome the shortcomings of Dijkstra’s algorithm, leading to extended versions, improved versions, and hybrids^{14,16,17,18,19}. Figure 5 illustrates a simple application of Dijkstra’s algorithm, showcasing how it calculates the optimal path within a graph-mapped domain. Dijkstra’s path planning algorithm is handy in autonomous vehicle navigation, robotics, GPS systems, network routing, and logistics for finding the shortest and most efficient paths.

Fig. 5

Dijkstra’s Algorithm.

WaveFront

The Wavefront algorithm is a path-planning algorithm popular in finding the optimum path in a discrete grid. The algorithm is a breadth-first search (BFS) based path planning algorithm that propagates the wavefront from the start point through the environment until it reaches the goal points while mapping the shortest path^20,21. A Wavefront environmental configuration for a robot showing a start point and goal point is depicted in Fig. 6, while Fig. 7 shows the generated path using the Wavefront algorithm. Each cell in the grid is assigned a value based on its distance from the start point. The algorithm updates the value of each cell as the wavefront propagates through the grid. By so doing, each new wave generates a higher value than the previous wave. The algorithm selects a target point on the map and follows the highest descent of wavefronts back to the sources to determine the shortest path^22,23. It analyzes the nearest neighbors first before extending the circle’s radius to distant regions. The algorithm discretizes its workspace as shown in Fig. 6 below (zero (0) designates a cell of free space, one (1) designates a cell fully occupied by an obstacle):

Fig. 6

Discretizes workspace of a Wavefront algorithm.

Fig. 7

Robot path generated with Wavefront Algorithm.

The Wavefront algorithm has good computation time, which is acceptable for real-time applications such as Unmanned Ground Vehicles (UGVs)²⁴. It is helpful in robotics for navigating complex environments, autonomous vacuum cleaners for efficient room mapping and cleaning, warehouse robotics for optimizing pick-and-place tasks, video game AI for character navigation, and disaster response robots for traversing hazardous areas²¹.

Rapidly-exploring random trees (RRT)

The RRT is a path-planning algorithm that uses a randomized data structure invented by Professor Dr. Steven LaVelle^25,26. It efficiently searches for paths in nonconvex high-dimensional spaces. RRT is constructed incrementally by expanding the tree to a randomly sampled point in the configuration space and avoiding obstacles. An RRT iteratively expands by attempting to connect a randomly selected node in the state space and a node in a tree closest to it. It randomly generates points and connects to the available node closest to the randomly generated point. When creating a vertex, it checks to ensure that it lies outside an obstacle and that the connecting path does not cross an obstacle, as shown in Fig. 9 below 25. The distribution of the vertices of an RRT is similar to the sampling distribution in a uniform distribution. Figure 8 depicts an RRT path. The RRT creates a graph and finds a path that may not be optimal (if evaluated based on time cost and path length). The RRT (Rapidly-Exploring Random Tree) path-planning algorithm is handy in autonomous vehicle navigation, mobile robot obstacle avoidance, warehouse logistics, robotic arm motion planning, and video game AI for efficient pathfinding.

Fig. 8

Robot path generated with Rapidly-Exploring Random Trees.

RRT algorithm picks the starting point of the robot (start configuration), marks it as the initial root node of the tree, and randomly selects a node based on the random sampling principle. It picks a new node along the direction of random nodes using the constraint conditions of the robot movement (such as step size and angle). The above process continues until the algorithm finds the goal point²⁷. The RRT algorithm expands as shown in Fig. 9 where x_start is an initial point; x_rand is a random point; x_nearest is a tree node closest to the random point, x_new and is a new node intercepted in steps on the line connecting x_nearest and x_rand.

Fig. 9

RRT Building process.

Algorithm 1

RRT Pseudo Code

Despite its weaknesses and limitations, RRT has some excellent properties that make it ideally suitable for various practical planning problems²⁵. These include,

• i. An RRT is probabilistically complete under very general conditions.

• ii. The expansion of an RRT is heavily biased toward unexplored portions of the state space.

• iii. The distribution of vertices in an RRT approaches the sampling distribution, leading to consistent and reliable behavior.

• iv. The RRT algorithm is relatively simple, facilitating performance analysis (this is also a preferred feature of the probabilistic roadmap).

• v. An RRT always remains connected, even though the number of edges is minimal.

• vi. An RRT can be considered a path-planning module that can be adapted and incorporated into various.

• vii. Planning systems.

RRT*

RRT* is an optimized version of RRT. Both algorithms operate on the same basic principle; however, RRT* has two additional key features that significantly differentiate it from RRT.

• i. RRT* keeps the distance of each vertex it has traveled relative to the parent vertex, referred to as the cost () of the vertex. After finding the closest node in the graph, then vertices in the neighborhood within a fixed radius from the new node are examined. If any node has a cheaper cost () than the proximal node, the cheaper node replaces the proximal node. This process continues until the goal point is reached, thus forming the robotic path. This feature eliminates RRT’s cubic structure, thereby yielding an optimized algorithm.

• ii. Additionally, in RRT*, after adding a vertex to the cheapest neighbor, the neighbors are re-examined to see if rewiring the newly added vertex will reduce the overall cost. If it does, the neighbor rewires to the newly added vertex. This feature smooths the generated path.

RRT* converges to the shortest path at the cost of more computation. The trees are probabilistically complete, meaning if a nonzero-width path exists, the tree will eventually find the path. It is of particular concern to researchers due to its asymptotic optimality. The main limitation of RRT* is that its convergence rate is slow, which makes it inefficient for applications. RRT* finds the initial path faster than RRT and optimizes it in subsequent iterations. When the number of iterations approaches infinity, an optimal or near-optimal path is generated²⁸. Figure 10 shows a mobile robot path generated with RRT*. RRT* may produce suboptimal paths and converge slowly for reasons below²⁹.

• i. In the initial iteration, the algorithm rejects the beneficial samples near the target region because, in the early iteration, it could not directly connect them to existing points in the tree;

• ii. Explore and sample in the whole configuration space so the sampling space is ample;

• iii. The number of points in the tree is large, and the memory demand is high;

• iv. Converge to the optimal path slowly.

Fig. 10

Robot path generated with RRT* Algorithm.

While an RRT algorithm can effectively find a feasible path, an RRT alone may not be appropriate to solve a path planning problem for a mobile robot as it cannot incorporate additional cost information such as smoothness or length of the path. Thus, it is a good component to incorporate into developing various planning algorithms, e.g., RRT*.

The RRT* path planning algorithm is helpful in autonomous vehicle navigation, mobile robot obstacle avoidance, warehouse logistics, video game AI, and UAV (Unmanned Aerial Vehicle) flight path optimization.

Artificial potential field (APF)

The APF algorithm is a path planning technique that creates a virtual force field (attractive and repulsive forces) around obstacles and the goal position in the environment that repels or attracts the robot depending on its position relative to the obstacle and the goal point. Equation 2 shows the APF function.

$${\mathbf{F}}\left( {\mathbf{q}} \right) = {\mathbf{F}}_{{{\mathbf{att}}}} \left( {\mathbf{q}} \right) + {\mathbf{F}}_{{{\mathbf{rep}}}} \left( {\mathbf{q}} \right)$$

(2)

The APF algorithm works on the principle that the target (goal position) creates a virtual potential that attracts and guides the robot towards it, and obstacles create a virtual potential that repels the robot. The repulsive potential is inversely proportional to the obstacle’s distance and makes a repulsive force that pushes the robot away from obstacles, as depicted in Fig. 11.

Fig. 11

APF forces around an obstacle.

The sum of all the forces acting on the robot moves it along the direction of the resultant force. The APF is one of the most significant and widespread path-planning algorithms due to its simplicity, elegance, easy implementation, use of a simple math model, low computational complexity, and good collision avoidance³⁰. The APF environmental configuration comprises attractive and repulsive potential that combine to guide the robot to the desired goal, as represented in Eq. 3.

$${\mathbf{U}}_{{{\mathbf{att}}}} \left( {\mathbf{q}} \right) + {\mathbf{U}}_{{{\mathbf{rep}}}} \left( {\mathbf{q}} \right) = {\mathbf{U}}\left( {\mathbf{q}} \right)$$

(3)

Oussama Khatib introduced the APF algorithm in 1985 as a potential-based approach for obstacle avoidance and path planning in his paper titled "Real-time obstacle avoidance for manipulators and mobile robots," which presented the fundamental principles of the APF method. The technique has a rich history in robotics and has undergone several advancements since its introduction. The successes of the APF in path planning for mobile robots have drawn the attention of several researchers whose aims are to extend, refine, and improve it, provide solutions to its limitations, and optimize its performance. These researches have yielded improved APF and hybrid techniques that handle dynamic obstacle avoidance, address local minima and deadlocks, and integrate with other path-planning and control techniques. These developments have made APF a versatile and widely used approach for path planning and obstacle avoidance in autonomous robotics in dynamic environments. As robotics advanced, researchers explored hybrid techniques by integrating the APF method with other planning and control techniques that improved path planning efficiency, handled complex environments, and considered robot dynamics²⁸. With the emergence of machine learning and deep learning techniques, researchers have also explored incorporating machine learning and other artificial intelligence techniques into the APF framework—for example, the combination of APF with reinforcement learning to optimize robots and the use of neural networks to learn and adapt the potential field representation²⁹.

The APF is a relatively mature algorithm, but it has some drawbacks. These include the robot getting trapped so it cannot progress towards the goal nor retract to the start point at a local minimum. The performance and effectiveness of APF heavily rely on the appropriate tuning of its parameters, oscillations, or vibrations when the robot approaches an obstacle or around local minima in the potential field, and the APF algorithm may struggle to handle dynamic obstacles because it is initially designed for a static environment. It is handy in Autonomous Vehicle Navigation (AVN), mobile robot obstacle avoidance, UAV (Unmanned Aerial Vehicle) flight path optimization, and cruise missile guidance systems.

Bug algorithm

The Bug algorithm is a class of motion planning algorithms that navigate a robot from a starting point to a goal in an environment with unknown obstacles. The key feature of Bug algorithms is that they work with the local sensing of the environment rather than global environmental knowledge by maintaining only local knowledge of the environment and a global goal position. The Bug algorithm performs its search for goal position using two essential behaviors: when not encountering obstacles, move along the line to the target (Bug1 Algorithm); when encountering obstacles, bypass the obstacles, use a specific judgment strategy to avoid obstacles, and continue to go straight towards the target (Bug2 Algorithm). By combining the two behaviors, the Bug algorithm can adjust the path planning strategy in real time to reach the endpoint. The main difference between different Bug algorithms is their obstacles bypassing and behavioral switching strategies. The Bug (Bug 1, Bug 2, and Tangent Bug) path planning algorithms are helpful in robotics for navigating unknown environments, warehouse logistics, and hazardous area exploration, particularly in rescue missions where robots need to find their way through dangerous areas autonomously^31,32,33,34.

Bug 1 algorithm

The basic principle of the Bug1 algorithm is that the algorithm obtains the shortest path along the line to the target (goal position) when there is no obstacle. When the algorithm encounters an obstacle, it first bypasses the entire border of the obstacle while marking the “leave point” (the closest position to the target point) and leaves obstacles from that point. Figure 12 shows the schematic diagram of the Bug1 algorithm. The algorithm marks the start point and the goal point. It then commences its navigation from the start point and continues to move along the line to the goal until it encounters an obstacle. When it encounters an obstacle, the position in which the robot hits the obstacle for the first time (the hit-point) is marked. Then, the robot detours the entire border of the obstacle and returns to the “hit point” while recording the closest point to the goal point (leave point") during the process of detouring. The robot moves to the point, leaves the obstacle from that point, and moves to the target along the line again^33,34.

Fig. 12

Robot path generated using Bug 1 Algorithm.

Bug 2 algorithm

The basic idea of the Bug2 algorithm is similar to the Bug1 algorithm. It optimizes the technique to bypass obstacles by creating a virtual straight line from the start to the goal point, usually called an "M-Line." When it encounters an obstacle, the path follows the border of the obstacle and then leaves the obstacle when it meets the M-line on the other side again. Figure 13 shows the schematic diagram of the Bug 2 algorithm. The algorithm marks the start and goal points and commences its navigation from the start point; the line connecting the start with the goal is called the M-line, which does not change with the robot’s movement. The robot continues to move along the line to the goal point until it encounters an obstacle. When it encounters an obstacle, the position where the robot meets the M-line closer to the goal point (the “leave point”) is marked. The robot moves to the point, leaves the obstacle without detouring the obstacle, and moves to the target along the line again^33,35.

Fig. 13

Robot path generated using Bug 2 Algorithm.

Tangent bug algorithm

The Tangent Bug Algorithm is a path-planning technique that is particularly effective when the robot has no global goal but only local information about the environment. It combines two behaviors: motion-to-goal and boundary following. In Motion-to-Goal, the robot moves directly toward the goal as long as there are no obstacles. When it encounters an obstacle, it follows the boundary of the obstacle until it can resume its motion toward the goal. Figure 14 depicts a robotic path generated with Tangent Bug Algorithms. The Tangent algorithm has three main features: the robot uses only the local information from its sensors (Local Knowledge), moves towards the goal or follows an obstacle boundary (Simple behavior), and guarantees that the robot reaches the goal if it exists^31,33.

Fig. 14

Robot path generated using Tangent Bug Algorithm.

Breadth-first search (BFS) algorithm

The Breadth-First Search (BFS) Algorithm is a fundamental graph traversal technique widely used in path planning, particularly effective in unweighted grid-based environments. It explores all nodes at the present depth level before moving on to nodes at the next depth level to ensure it finds the shortest path with the fewest edges. The BFS algorithm has been widely used in research to provide alternative solutions for the shortest path solution and intelligent route planning in industrial robotics to optimally find the fastest route/path (shortest path) for the robot to arrive at the endpoint (goal point). BFS path planning algorithms are commonly used for navigating autonomous robots through mazes and complex environments, as well as in swarm robotics, where multiple robots operate together in a coordinated manner to ensure efficient area coverage during tasks like search-and-rescue missions^36,37. Figure 15 depicts a BFS path for a mobile robot.

Fig. 15

Robot path generated using Breadth-First Search (BFS) Algorithm.

Depth-first search (DFS) algorithm

Depth-first search (DFS) is a graph search algorithm that explores each branch as far as possible in a depth-first manner before backtracking. DFS does not guarantee the shortest path to the goal node, but it can be more efficient than BFS in some instances, especially when the goal node is close to the initial node. DFS-based path planning methods use the Depth-First Search algorithm to explore the state space in a depth-first manner, which can lead to a shorter/optimal path⁵². DFS is a deterministic, non-heuristic algorithm that returns the first direct path between two points without assessing the environment to determine the best option. The algorithm explores a node and all its descendants at a time. It starts by selecting a node and expands its search onto the deepest nodes from the last until there are no more child elements to explore. If the deepest node does not contain the solution the algorithm is searching for, it reverses back to the start of the tree. It continues to the adjacent node on the right in the same “deep” format, traversing downward and, when necessary, “backtracking” upward to continue the search. The DFS algorithms in robotics are suitable for exploring unknown environments or mapping out all possible routes in complex terrains to ensure a thorough search of paths or obstacles. In addition to mapping out routes and exploring unknown terrains, DFS algorithms are also useful for robotic arm motion planning in industrial automation. It enables precise pathfinding through layers of complex tasks and AI-driven games where robots need to traverse intricate mazes or obstacles³⁸. Figure 16 shows a DFS-generated path in our sample environment.

Fig. 16

Robot path generated using DFS Algorithm.

Bidirectional depth-first search (BFS) algorithm

Bidirectional Breath-First Search (BFS) is an advanced search algorithm that enhances the traditional BFS by simultaneously exploring from both the start and goal nodes. Unlike the conventional BFS that explores all nodes at the present depth level before moving on to nodes at the next depth level, the dual approach aims to meet in the middle, thereby significantly reducing the search space and time complexity, as shown in Fig. 17 below. In practice, this has a massive positive impact on performance in most real-world applications that can be useful in specific scenarios where the goal lies at a deeper level of the graph. Bidirectional BFS algorithms are deployed in robots to optimize search and rescue operations. For example, robots deployed to find persons trapped in a collapsed building simultaneously search from both the entrance and the last known position of the person to find a path through the debris quickly. This two-way exploration reduces search time and improves the robot’s efficiency in critical scenarios^37,39.

Fig. 17

Robot path generated using Bidirectional BFS Algorithm.

Bidirectional A* (BA*) algorithm

The Bidirectional A* algorithm is an enhancement of the traditional A* search algorithm that simultaneously searches both forward from the initial state and backward from the goal and stops searching when the two searches meet in the middle to reduce the search space, time complexity, and improve efficiency significantly^40,41. In such a condition, bidirectional A* is usually faster than unidirectional A* in finding a route. The BA algorithms are used in warehouse automation, autonomous vehicle routing, and autonomous drone navigation, enabling efficient route planning for aerial surveillance and delivery services. They are also helpful in optimizing traffic flow for self-driving cars, allowing them to navigate urban environments swiftly and safely by reducing the computation time required to find the best routes. Whether in the skies or on the roads, BA ensures robots can make smart, quick decisions⁴². Figure 18 below depicts a bidirectional A* path.

Fig. 18

Robot path generated using BA Algorithm.

Voronoi road map (VRM)

Algorithm leverages the concept of Voronoi diagrams that logically partition the geometric space into regions (containing all points closest to a particular seed point) based on the distance to a set of predefined points, such that the boundaries of the resultant regions are as far away as possible from all obstacles. The partition creates a network of edges that are equidistant from the nearest obstacles and provides a natural clearance from obstacles. The VRM algorithm uses the edges of the Voronoi diagram to create a roadmap. The VRM uses the roadmap to find a path from the start to the goal position while ensuring the path maintains a safe distance from obstacles. The Voronoi Road Map (VRM) algorithms are deployed in robotics to navigate through dynamic environments by mapping out safe, collision-free pathways, making them ideal for applications like automated warehouse systems, agricultural robotics for precision farming, urban planning to optimize, smooth and collision-free paths in crowded pedestrian areas or parks, autonomous drone flight planning^43,44. Figure 19 shows a VRM path.

Fig. 19

Robot path generated using VRM algorithm.

The VRM path planning algorithm is handy in multi-robot region coverage, optimizing routes for efficient environmental sensing, target searching, and large-scale vehicle routing optimization with time constraints⁴⁵.

Heuristic algorithm

Heuristic algorithms help decrease the time complexity of NP problems and find quick solutions to such issues. They are commonly helpful in artificial intelligence problems that require an informed search, where additional information is available to guide the next step toward finding a solution. It may not produce the best solution, but it will give a near-optimal solution quickly. Heuristic algorithms are suitable where other techniques can not provide solutions. The heuristic path planning algorithms are well-suited for NP-Hard problems without known solutions. They employ a heuristic function to derive a heuristic value, guiding the technique toward an optimal solution by leveraging these values to move closer to the goal while seeking the optimal path^5,46. The heuristic approaches are more intelligent and innovative than classical methods because they can adapt to dynamic environments with uncertain or incomplete information. The main limitation of the heuristic method is its long learning phase and high computational time. Given the limited computational capacity of most robot controllers, these approaches increase computational cost. However, as with increasing computational power, this concern is mainly confined to small, fast robots.

A^* algorithm

Hart, Nilsson, and Raphael introduced the A* algorithm 1968. It derives its name from its two key features: "A" for "Admissible," referencing its use of an admissible heuristic to estimate distance costs, and "*" to signify its combination of actual and estimated costs for informed search decisions during the search process. It is renowned for using a heuristic function and an evaluation function f(n) to determine the next node to expand and to guide its search for the optimal path. Figure 20 shows an optimal path generated using the A* algorithm with obstacle avoidance features. The A* is famous for its completeness, optimality, and efficiency attributes. It guarantees finding a solution if one exists (completeness), finding the optimal path with the lowest cost (optimality), and efficiently exploring fewer nodes by utilizing heuristics (efficiency). It is a best-first search algorithm with the idea of maintaining a priority queue of nodes to be expanded based on the node with the lowest cost (shortest distance) using the function in Eq. 4 below^37,47.

$${\varvec{f}}\left( {\varvec{n}} \right) = {\varvec{g}}\left( {\varvec{n}} \right) + {\varvec{h}}\left( {\varvec{n}} \right)$$

(4)

Fig. 20

Robot path generated with A* Algorithm.

where g(n) is the cost of the path from the start node to node n, and h(n) is an estimate of the cost of the cheapest path from n to the goal.

The A* algorithm is an extension of the Dijkstra algorithm, as depicted in Fig. 21.

Fig. 21

A* Algorithm = Dijkstra’s algorithm + educated guess of distance from the current point to the goal position.

f(n) = the total cost estimate from the start note to the target node through the n node.

g(n) = actual cost from start node to n node.

h(n) = estimated cost from node n to target node (Heuristic function).

Like other algorithms, inherent limitations of the Dijkstra algorithm include slow planning speed, poor path smoothness, slow speed due to right-angle turns, and planned path too close to obstacles (poor clearance)^47,48. Much research has successfully improved or overcome some of the challenges of the A* algorithm^47,49,50. These challenges adversely affect the performance of the A* algorithm, which reduces the robustness of the planned path and limits its adoption; however, when successfully applied, it is very reliable and produces an efficient optimal path ⁴⁷. A* algorithm is handy in varying aspects and fields of life, such as autonomous vehicle navigation, robot arm manipulation, game AI, and Military and commercial applications^49,51,52. The running time of an A* algorithm is faster than that of Dijkstra’s algorithm because of its principle that selects the location point based on the best heuristic value. Finally, the complexity of Dijkstra’s and A* algorithms is considered equivalent⁵¹. The A* algorithm uses a best-first search technique to create a path with the least cost from a given start point to the goal point. It has high accuracy because it considers the already calculated sectors and finds the least-cost track to the sector, making it a best-first search algorithm⁵². The A* path planning algorithm is helpful in autonomous vehicle navigation, medical drug delivery, robotic vacuum cleaners, post-disaster rescue, robotics for optimizing autonomous navigation in dynamic environments, and mining detection due to its robust search capability and guaranteed path optimality.

D* (D (Dynamic A)**)

D* is a sensor-based algorithm that handles dynamic obstacles by transforming its edge’s weights to form a temporal map in real-time. Afterward, it moves the robot from its current place to the goal location in the shortest unblocked (obstacle-free) path. It helps generate collision-free paths in the presence of moving obstacles. Like A*, D ∗ assesses the navigation cost by considering the post-calculation and forward estimation. It preserves a list of states that it uses to propagate information about modifications of the arcs cost function⁴. Figure 22 depicts a D* robotic path from the start to the goal point. The main goal of D* is to find an optimal path while accounting for dynamic changes in the environment. It is reliable in problems requiring cost map modifications (representing obstacles and terrain) during execution. It is often referred to as a cost map repair algorithm because it incrementally repairs the cost map based on new environmental information, such as changes in obstacle positions, terrain conditions, and other environmental changes, allowing it to handle dynamic scenarios. The D* employs an informed incremental search strategy; rather than recalculating the entire path from scratch, it incrementally updates the existing path based on new information. This approach is efficient and suitable for real-time applications. The affected portions of the path are repaired rather than recomputation. This partial repair minimizes computational overhead and ensures responsiveness to dynamic changes. The D* considers moving obstacles by adjusting the path around them. It dynamically adapts to avoid collisions with these obstacles while maintaining optimality. Compared with A*, which assumes a static environment, D* accounts for changes. It is helpful in scenarios where obstacles move or the environment is uncertain. The D* is a valuable tool for mobile robots navigating dynamic environments. It combines informed search, cost map repair, and adaptability to provide efficient, collision-free paths.

Fig. 22

Robot path generated with D* Algorithm.

D* Lite

The D* Lite algorithm combines heuristic and incremental search techniques and implements navigation tasks in a dynamic environment. It offers a solution to avoid static obstacles that appeared initially or during the robot’s walking but cannot handle moving obstacles. Figure 23 shows a D* lite path for a mobile robot. The following are some of the biggest challenges of robot path planning using the D* lite in unknown environments⁵³:

• The D* lite gives a superior optimal solution if the map of its environment is static or changes slightly. When the map changes excessively, the time consumed for repairing and re-generating the path is usually longer than when re-planning afresh. The long re-planning time may lead to path search failure when there are repeated changes in the map.

• It may perform poorly when the map unexpectedly changes. The effectiveness may be low when the map has many dynamic obstacles. These are prevalent occurrences in a conflict-based search algorithm that adopts a centralized global planning strategy and requires preplanning for the paths.

• Few path planning algorithms can give superior performance in unknown dynamic environments for multi-metric evaluation, such as the success rate of pathfinding, the number of collision avoidances, the time step, etc.

Fig. 23

Robot path generated with D* Lite Algorithm.

The D* Lite path planning algorithms are helpful in robotics for dynamic path re-planning. They allow robots like autonomous vehicles and delivery drones to adapt to changes in their environment efficiently, ensuring smooth and uninterrupted navigation.

Metaheuristic algorithms

Metaheuristic algorithms are optimization algorithms used to find the optimal solution for complex problems where the information or knowledge of the problem under consideration is insufficient or unavailable. The algorithms draw inspiration from natural phenomena such as genetics, swarm behavior, and evolution. They are handy in most optimization problems, highly nonlinear and discrete problems. These algorithms can be classified based on different criteria such as nature-inspired vs. non-nature-inspired, single-solution vs. population-based, deterministic vs. stochastic, Trajectory-based vs. population-based, and local search-based vs. global search-base⁵⁴. Metaheuristics algorithms have been helpful to a wide range of optimization problems in various fields, such as engineering, finance, computer science, robotics, logistics, and healthcare.

Some of the merits of metaheuristic algorithms are that they can search large and complex solution spaces and find suitable solutions where other methods may not find a solution. They can handle nonlinear and non-differentiable problems because they do not require the objective function to be differentiable. Additionally, metaheuristic algorithms can help to exploit the power of modern parallel computing architectures. Furthermore, metaheuristic algorithms are generally robust to noise and uncertainties in the optimization problem. On the other hand, some demerits of metaheuristics are that they do not guarantee optimal solutions to an optimization problem. They may find a good solution, but it is usually not the best possible one. Metaheuristic algorithms can be computationally expensive, especially for large-scale optimization problems.

Additionally, finding optimal values for several parameters that require turning to achieve good performance is always challenging. Furthermore, metaheuristic algorithms do not expose their underlying structure; they are a black-box approach that searches for reasonable solutions without sharing information on its approaches [Overview of Metaheuristic Algorithms]. Incorporating appropriate strategies into their objective functions or fitness evaluations of Metaheuristic algorithms can be helpful in more complex problems^55,56.

Cuckoo search algorithm

The Cuckoo Search (CS) algorithm is a nature-inspired optimization algorithm developed by Xin-She Yang and Suash Deb in 2009. Its inspiration is from the brood parasitism of some cuckoo species, where they lay their eggs in the nests of other host birds. If a host bird discovers the eggs are not its own, it will either throw them away or abandon the nest and build a new one. The CS algorithm uses this behavior to find optimal solutions to complex optimization problems. If the eggs hatch successfully, the cuckoo chicks push the host’s eggs out of the nest during their growth process^54,57.

Algorithm 2

Cuckoo Search (CA) Pseudo Code

Firefly algorithm (FA)

Developed by Xin-She Yang in 2008, the FA is inspired by the flashing behavior of fireflies in nature (bioluminescence), emitting light to attract prey and mates or ward off enemies^54,56.

Algorithm 3

Firefly Algorithm (FA) Pseudo Code

Particle swam optimization (PSO)

Proposed by Ames Kennedy and Russell Eberhart in 1995. PSO Emulating the flocking behavior of birds or schooling of fish. Its population-based approach leverages the dynamic exchange of information between individual particles, akin to birds sharing their velocity and position within the flock^54,56.

Algorithm 4

Particle Swam Optimization (PSO) Pseudo code

Whale optimization algorithm (WOA)

Developed by Seyedali Mirjalili and Andrew Lewis in 2016, the WOA is inspired by humpback whales’ social behavior and bubble-net hunting strategy. This algorithm solves optimization problems by mimicking whale hunting behavior⁵⁴.

Algorithm 5

Whale Optimization Algorithm (WOA) Pseudo code

Genetic algorithm (GA)

GA is a natural-inspired optimization algorithm developed by John Holland in the 1960s and further refined by his students and colleagues. It is inspired by natural selection and genetics. GA solves optimization problems by evolving a population of candidate solutions over generations^54,58.

Algorithm 6

Genetic Algorithm (GA) Pseudo code

Ant colony optimization (ACO)

Marco Dorigo developed the ACO in the early 1990s. Its inspiration came from ants’ foraging behavior, particularly their ability to find the shortest path between their nest and a food source using pheromone trails. The ACO solves optimization problems by simulating how ants search for food and communicate with each other⁵⁸.

Algorithm 7

Ant Colony Optimization (ACO) Pseudo code

Tabu search (TS)

Tabu Search (TS) is a metaheuristic optimization algorithm developed by Fred W. Glover in 1986. It solves complex optimization problems by guiding a local search procedure to explore the solution space beyond local optimality. TS uses memory structures to avoid cycling back to previously visited solutions and to escape local optima⁵⁶.

Algorithm 8

Tabu Search (TS) Pseudo code

Harmony search (HS)

Harmony Search (HS) is a nature-inspired optimization algorithm developed by Zong Woo Geem, Joong Hoon Kim, and G. V. Loganathan in 2001. Its inspiration is from the musical process of searching for a perfect state of harmony, such as when musicians improvise to find a harmonious melody. HS is used to solve optimization problems by mimicking the way musicians adjust their pitches to achieve harmony⁵⁶.

Algorithm 9

Harmony Search (HS) Pseudo code

Differential evaluation (DE)

Differential Evolution (DE) is a population-based optimization algorithm developed by Rainer Storn and Kenneth Price in 1995. It solves complex optimization problems by iteratively improving a population of candidate solutions. DE is known for its simplicity, robustness, and efficiency in finding optimal solutions.

Algorithm 10

Differential Evalution (DE) Pseudo code

Dragonfly algorithm (DA)

The Dragonfly Algorithm (DA) is a metaheuristic optimization technique inspired by the static and dynamic swarming behaviors of dragonflies in nature. It was developed by Seyedali Mirjalili in 2015 and is designed to solve single-objective, discrete, and multi-objective optimization problems and find paths that avoid obstacles⁵⁶.

Algorithm 11

Differential Evalution (DE) Pseudo code

The strengths and challenges of path planning algorithms

Each of the three broad classifications of path planning algorithms have their strengths and challenges. These are summarized in Table 1 below^{54,55,57,59,60}.

Table 1 Summarized strengths and challenges of path planning classifications.

Experiments and results

In this section, we present the simulations and comparative implementation results of eighteen (18) notable path-planning algorithms in the same environmental configuration (the same number of obstacles in the same arrangement, the same start and goal points, etc.). Table 2 presents the different algorithms’ resultant path length and corresponding completion time.

Table 2 The results of the simulated planning algorithm in environmental configurations (_start (0,0) and _goal (167,140)) are shown in Fig. 24.

Fig. 24

Schematic show of first simulation environmental configuration.

Simulation environment configuration

The simulation environment’s configuration has obstacles arranged in strategically challenging positions, as depicted in Fig. 24, to ensure that the path generation employs obstacle avoidance techniques. All eighteen (18) planning algorithms were implemented using the Python development environment and simulated in the same environmental configuration shown below.

Simulation results

Consider the environmental configurations indicated in Eq. 5 below for the eighteen (18) planning algorithms.

$${\text{F}}\left( {q_{i} } \right) = {\text{Qi}}\left( {{\text{X}},{\text{ Y}},{\text{ Oj}}} \right)$$

(5)

where $i=1, 2, 3,\dots 18.$

The path planning algorithm commences from the initial position ${q}_{0}$, point (${x}_{0}$, ${y}_{0}$) in all the simulations. As the path generation progresses to the goal point, $\text{F}\left({q}_{i}\right)$ represents the positions of all the obstacles the ${O}_{j}$ = (${o}_{x}, {o}_{y}$) to generate an effective avoidance. The resultant path $\text{F}\left({q}_{i}\right)=(\left[{x}_{0}, {y}_{0}\right], \left[{x}_{1}, {y}_{1}\right], \dots \left[{x}_{n}, {y}_{n}\right] )$ with start point = $\left[{x}_{0}, {y}_{0}\right]$ and goal position = $\left[{x}_{n}, {y}_{n}\right]$ for each algorithm. The simulation implementation evaluates the path length and time to generate the path $\text{F}\left({q}_{i}\right)$.

The resultant path for the different planning algorithms is depicted in Fig. 25a–r below. Table 2 shows the measures (path length in meters and time in seconds) for the simulation results of the notable algorithms in the first simulation environment. Figure 26 and Fig. 27 are the bar chats of the notable algorithms’ path length and planning time, respectively. Table 3 depicts notable path planning algorithms’ performance evaluation results (clearance, collision risk, jerk, smoothness, curvature jerk, and others) in the first simulation environment. Figure 28 is the line chart of performance measures (Average Jerk, Average Curvature, Average Collision Risk, and Safety Scores) of notable path planning Algorithms. Figure 29 depicts the line chart of notable planning algorithms’ performance measures (Number of Turns/Bends and Average Clearance).

Fig. 25

(a) Dijkstra path. (b) A* path. (c) RRT path. (d) WaveFront path. (e) D* path. (f) RRT* path. (g) APF path. (h) Bug 1 path. (i) Bug 2 path. (j) D* path. (k) Tangental path. (l) BFS path. (m) DFS path. (n) PRM path. (O) Bidirectional A* path. (p) VRM path. (q) Bidirectional BFS. (r) Greedy BFS path.

Fig. 26

Chart of notable path planning Algorithms vs. time taken in seconds.

Fig. 27

Chart of notable path planning Algorithms vs. path Length in meters.

Table 3 Results of performance evaluation (clearance, collision risk, jerk, smoothness, curvature jerk, and others) of notable path planning algorithms in the first simulation environment.

Fig. 28

Chart of notable of performance measures (Average Jerk, Average Curvature, Average Collision Risk and safety Scores) of path planning Algorithms.

Fig. 29

Line chart of performance measures (Number of Turns/Bends and Average Clearance) of notable planning algorithms.

Explanation of simulation measures and parameters

In this section, we briefly explain our comparison measures and parameters.

(1) The planning time was recorded in seconds, starting from the commencement of the path planning to the point where the full path to the goal position was generated. It was built into the implementation code to ensure that the system pucks the start time and end time of each algorithm to ensure accuracy and eliminate human errors.

(2) Path Length: The total distance covered along a path. It measures how long a path is from the starting point to the goal position, including all the intermediate points or segments along the pathway. It is measured in meters and was computed by the system using the standard library in the Python program. The path length (L) function for a given points $\left( {x_{1} ,y_{1} } \right),\left( {x_{2} ,y_{2} } \right),...,\left( {x_{n} ,y_{n} } \right)$ is shown in Eq. 6.

$$L = \sum\limits_{k = 0}^{n} {\sqrt {\left( {x_{i + 1} - x_{i} } \right)^{2} + \left( {y_{i + 1} - y_{i} } \right)^{2} } }$$

(6)

For a parametric curve $r\left( t \right) = \left( {x(t),y(t)} \right)$, the path length L is shown in Eq. 7

$$L = \int\limits_{a}^{b} {\left( {\frac{dx}{{dt}}} \right)^{2} + \left( {\frac{dy}{{dt}}} \right)^{2} dt}$$

(7)

A shorter path is preferred because it is assumed to minimize energy consumption if all other variables are constant.

(3) Curvature: Measures how sharply a path bends or changes direction. A lower average curvature indicates a smoother path. Table 4 below shows the value range for curvature (k).

Table 4 Value range for curvature (k) of a robotic path.

(4) Number of Turn: The Number of Turns refers to the total count of directional changes or angular deviations in a path from the start point to the goal point. This metric is crucial for understanding the complexity and navigability of a path, especially for automated systems. Fewer turns usually mean a smoother path.

(5) Jerk: refers to the rate of change of acceleration over time. It is essentially the third derivative of position with respect to time or the first derivative of acceleration. Lower jerk values indicate smoother transitions. Table 5 below shows the value range classification for jerk in Robots.

Table 5 Value range for jerk (J) of a robotic path.

(6) Total Deviation: Represents the deviation from a straight line between start and goal points. Smaller deviations indicate smoother paths. Equation 8 is the function for total deviation of a path.

$${\text{Total Deviation }} = \sum\limits_{k = 0}^{n} {d_{i} }$$

(8)

where $d_{i}$ is the deviation at the $i^{ - th}$ point, and $n$ is the total number of points along the path.

(7) Collision Risk: evaluates the likelihood of robot to collide with an obstacle in the environment while moving through the generated paths. Table 6 below shows the value range that guided the interpretation of the outcomes of our simulation results.

Table 6 Value range for collision risk of a path.

(8) Safety Score: the safety score of the paths, which quantifies how safe a path is for a robot, taking into account various factors that could lead to collisions and helps to determine the collision risk level associated with the path as classified in Table 6^61,62.

Second simulation environment configuration

Figure 30 shows the configuration and obstacle arrangement for the second simulation, demonstrating that the planning algorithms’ obstacle avoidance techniques are in the new configuration. Similarly, Fig. 31a–h shows the generated path using selected algorithms in the second simulation environment. Figures 32 and 33 depict the Charts of the algorithms’ planning time and path length, respectively, as recorded in Table 7. Figures 34 and 35 show the performance measures (Average Jerk, Average Curvature, Average Collision Risk, Number of Turns (Bends), Average Clearance, and safety Scores) of notable path planning Algorithms in the second simulation environment as recorded in Table 8.

Fig. 30

Schematic show of second simulation environmental configuration.

Fig. 31

(a) Dijkstra path. (b) D* path. (c) Greedy BFS path. (d) Bidirectional BFS path. (e) RRT* path. (f) Bug 2 path. (g) PRM path. (h) Wavefront path.

Fig. 32

Chart of notable path planning Algorithms vs. time taken in seconds.

Fig. 33

Chart of notable path planning Algorithms vs. path length in meters.

Table 7 The results of the simulated planning algorithm in environmental configurations (start (0,0) and goal (167,140)) are shown in Fig. 30.

Fig. 34

Chart of notable path planning Algorithms’ Average Jerk, Average Curvature, Average Collision Risk and safety Scores.

Fig. 35

Chart of notable path planning Algorithms’ Number of Turns (Bends), and Average Clearance.

Table 8 Results of performance measures (clearance, collision risk, jerk, smoothness, curvature jerk and others) notable path planning algorithms in the second simulation environment.

Results and discussion

Each notable path-planning algorithm was simulated in the two simulation environment configured with obstacles arranged in strategically challenging positions, as depicted in Figs. 24 and 30. The simulation helps us evaluate the performance of the notable path-planning algorithms (in terms of path length and planning time). Figures 26a–r present the generated path for the mobile robot using the various path-planning algorithms. Table 2 presents the summarized result data for planning time and path length. Figure 26 and Fig. 27 represent the bar charts of the planning algorithms against planning time in seconds (s) and generated path length in meters (m), respectively.

The Wavefront planning algorithm recorded the shortest planning time of 0.21 s. However, its path length of 307 m was not the shortest compared to the 251.29 m length recorded by D* lite. The performance of the Wavefront algorithm is due to the simplicity of its path planning technique, where the wave expands uniformly from the start point and marks cells with increasing values until it reaches the goal point. Then, the path is traced back by following the steepest descent toward the adjacent cells with the lowest values to ensure the shortest path for robots^21,22,23.

On the other hand, RRT and RRT* recorded the longest planning time of 675.46 s and 641.12 s respectively, but yielded moderate path lengths of 281.52 m and 307.14 m respectively on average, because their paths change with every repeated simulation due to the inherent randomness in their path generation technique. The algorithms’ major limitation of high computational complexity, especially in a complex and extensive area like our simulation environment, may cause a high planning time of^63,64,65. The VRM is the second worst-performed algorithm in planning time, with a completion time of 494.31 s. However, it had a better path length of 331.02 m, shorter than some algorithms that finished in good record time, like the DFS algorithm that generated a path that was 423.91 m long but completed its planning in a record time of 54.50 s.

The Dijkstra, A*, and Bidirectional A* generated paths of equal length (263.99 m) to confirm their similarity in path generation technique and that A* is an extension/improvement on the Dijkstra algorithm⁷⁶. The above assertion is confirmed by the planning time of the two algorithms (205.53 for Dijkstra and 46.38 for A*, which shows excellent improvement in the planning time of the former). Similarly, the BFS Bidirectional BFS generated a path of equal length (263.99 M). However, the Greedy BFS yielded a longer path in a shorter time. The A* and the BFS path were equal to 262.99 m, affirming that the A* (A-star) algorithm is an informed search algorithm that combines the best features of both DFS and BFS³⁷.

Using a bidirectional approach to implement path planning techniques resulted in more significant improvements in planning time than using a unidirectional approach. This improvement was evident in the A* and Bidirectional A* results, which yielded 44.38 s and 4.93 s planning time, respectively. The manifestation is the same in BFS and Bidirectional BFS, with planning times of 12.45 s and 6.74 s, respectively^37,66.

The VRM took the longest time of 494.31 s to complete its planning. However, it yielded a path of 331.03 m length, which is way shorter than the 1336.0 m path length generated by Bug 1 in a shorter time of 212.56 s. The D* and D* lite showed similar results, with D* completing its planning in 14.45 s, which is less than 86.84 s taken by D* lite, but D* generated a path of 257.38 m long, while D* lite had a shorter route of 251.29 m long. BFS, DFS, PRM, and A* demonstrated a similar relationship. The planning technique with the worst planning time may not yield the worst (longest) path length; other factors, like the avoidance technique, search method, etc., affect the overall result.

Evaluation of the various performance measures for both simulation environment shows that all the paths are free of collision risk with good clearance score above 3, except bus 1 and Bug 2 algorithm in simulation environment two. Similarly, the jerk measure of the algorithms are within acceptable range except RRT and RRT* with Average jerk values of 2.9179 m/s³ and 3.2658 m/s³ respectively. In simulation environment two, the APF encountered oscillation issue and could not generate a path, even though a feasible path exists. Oscillation issues is one of the limitations of APF algorithm.

Future outlook of path planning algorithms

In recent years, technology has commenced a positive journey toward intelligent systems capable of conducting analysis and projections, making complex judgments based on past experiences, and making informed projections and decisions in their problem domains. Like every other field, mobile robots have witnessed rapid adoption of artificial intelligence (AI) techniques to make more intelligent and brilliant robots⁵⁸. These advancements have shifted the main aim of path planning from practical obstacle avoidance to path generation speed, efficiency of the optimum path, ability of the robot to apply previous knowledge to an entirely new environment, deal with emergencies, ability to extract information from the surrounding environment to make corresponding action decision. These potentials and the exciting possibilities of the future of this field have continued to attract researchers into different technology combinations (Machine learning (ML), AIs, Deep Learning (DL), Re-enforce Learning (RL), Deep re-enforce learning (DRL), etc.) will yield more efficient, intelligent and sophisticated path planning techniques for mobile robot. The current display of these outcomes in modern drone fighter planes, which exemplifies the use of AI technology in modern robot operations, is just the tip of the iceberg. Figure 36 shows both the domestic and foreign academic achievements of in mobile robot path planning in China⁶⁷.

Fig. 36

Mobile robot path planning academic achievements in China: (a) Domestic; (b) Foreign⁶⁷.

Conclusion

This paper carefully classifies notable path-planning algorithms, discusses their basic classifications, principles, fundamental features, and challenges, suggests some real-life applications, and implements each in a simulation environment configured with obstacles arranged in strategically challenging positions. The choice of a planning algorithm depends more on the nature of the problem, the complexity and size of the environment, the number of obstacles (single or multiple), and the arrangements of obstacles. The simulated results revealed that the algorithm with the best planning time did not generate the shortest path length. Similarly, those that yielded equal path length delivered it at different planning times. Robotic path planners should study the problem domain to choose the planning technique because the path planning time, path length, and other attributes of any path planning algorithm change, such as the dimension, nature, number, and arrangement of obstacles in the problem domain changes.