Abstract
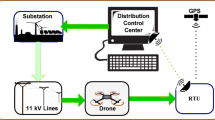
For the insulator discharge severity assessment at the line inspection site using edge-end computing equipment and UV cameras, this paper proposes an improved assessment algorithm based on the YOLOv8 algorithm. Firstly, LDConv is introduced to replace the convolution of the backbone network part of the network feature extraction, which effectively realizes the enhancement of the feature extraction ability of the algorithm in the case of model lightweighting; and then ACMix attention mechanism is introduced, which realizes better focusing of the model on the target with a very small performance loss; and finally, Shape-IoU is introduced to replace the loss function of the CIoU, which effectively improve the detection accuracy of the algorithm. The experimental results show that compared with the original YOLOv8, the RDIDSNet algorithm proposed in this paper achieves a detection speed of 61 Frames/s while realizing a detection accuracy of 78.1%, which can satisfy the demand for fast and accurate assessment of insulator discharge severity on edge devices.
Similar content being viewed by others
Introduction
Insulators are key components in the power system to ensure the safe operation of transmission lines, and their performance directly affects the stability and reliability of the power grid. However, in the process of long-term operation, affected by environmental pollution, aging and external damage and other factors, insulator surface discharge phenomenon may occur, and in serious cases, it may even lead to line failure, threatening the safety of the power grid. Therefore, timely and accurate assessment of the severity of insulator discharge is of great significance to ensure the reliable operation of the power system. In recent years, with the rapid development of deep learning technology, it has shown excellent performance in the field of image processing and pattern recognition. Applying deep learning technology to insulator discharge severity assessment can not only improve the detection accuracy, but also realize fast and automated fault diagnosis, providing an efficient and reliable solution for power inspection.
There has been substantial research on the detection and evaluation of insulator discharges. For instance, Guo et al.1 employed the Local Mean Decomposition(LMD) and Long Short-Term Memory(LSTM) machine learning methods to achieve precise classification and diagnosis of insulator discharge conditions. Tan et al.2 proposed utilizing multiple nonlinear transformations to improve the convolutional kernels for feature extraction, thereby lightening the model and significantly enhancing the accuracy of insulator discharge detection. Wang et al.3 and Lü et al.4 introduced ultraviolet discharge imaging and deep learning into the evaluation of insulator discharges, leveraging an adaptive learning rate update mechanism to optimize the Single Shot multibox Detectot(SSD) and YOLOv3 algorithms, which enabled high-accuracy diagnosis of insulator discharge severity. Furthermore, Yang et al.5 proposed improvements to the YOLOv8 algorithm model using the Mosaic-9 data augmentation method, the GhostNet network, as well as GeLU and Smoothed Intersection over Union(SIoU) loss functions. These enhancements significantly increased the inference speed of the model, achieving rapid evaluation of insulator discharges.
Although some research has been conducted on evaluating the severity of insulator discharges, most methods based on partial discharge signals rely on leakage current sensors. Due to their high cost and immobility, these sensors are unsuitable for on-site power inspection scenarios. While current studies on ultraviolet (UV) image-based methods have proposed lightweight severity evaluation algorithms based on YOLOv8, they primarily focus on model simplification without simultaneously improving both speed and accuracy.
To address the shortcomings of existing research and meet the on-site requirements for evaluating insulator discharge severity using edge devices, this paper proposes the Rapid Detection of Insulator Discharge Severity Network (RDIDSNet). Based on the YOLOv8 algorithm, the convolutional layers of the YOLOv86 network are enhanced by introducing Linear Deformable Convolution(LDConv), which significantly reduces the model’s overall parameters and computational cost while improving detection accuracy. Additionally, the self-Attention and Convolution Mixed module(ACMix) attention mechanism is integrated, allowing the model to focus on targets with minimal computational overhead, effectively addressing issues of poor localization and low detection accuracy. Finally, the model’s loss function is modified by replacing the Complete Intersection over Union(CIoU) loss function with the Shape-IoU loss function, which mitigates the interference of irregular discharge spot shapes in UV insulator images on the precision of bounding boxes. This results in a high-speed, high-accuracy method for rapid insulator discharge detection.
RDIDSNet network
YOLOv8 network
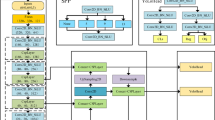
The YOLOv8 algorithm, developed by the YOLOv5 research team, is a State-Of-The-Art (SOTA) method in the field of object detection. YOLOv8 algorithm still follows the tradition of YOLO series in its structure, i.e., firstly, feature extraction is performed using the backbone CNN network, and then feature fusion is performed in the neck network, and some of the improved algorithms of the neck network will additionally add the attention mechanism7 in order to improve the detection accuracy of the algorithm, and finally, the head network is utilized for the detection and output. In the Backbone component, the algorithm incorporates a newly designed C2F module to enhance gradient flow richness. For the Neck component, it integrates concepts from BiFPN8 while removing the traditional head-to-tail convolutional connection layers. In the Head component, YOLOv8 draws inspiration from the YOLOX algorithm, adopting a decoupled head structure and an anchor-free framework. Additionally, it replaces the Intersection over Union (IoU)-based static sample assignment with the Task-Aligned Assigner9 dynamic sample assignment strategy for positive and negative sample allocation. The loss function combines distribution focal loss (DFL)10 with the CIoU loss function11, significantly improving YOLOv8’s detection accuracy.
Currently, YOLOv8 and its variants have been widely applied in power industry research12,13,14. Given the need to use edge computing modules and ultraviolet (UV) cameras to accurately locate and evaluate the severity of insulator discharges, it is crucial to achieve high processing speed and robust performance against irregular discharge spots. Therefore, YOLOv8 requires modifications tailored to practical application demands. The network structure is shown in the figure below.
LDConv
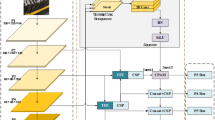
To address the above issues, we propose using the LDConv module15 to replace parts of the convolution layers in the feature extraction component of the model, specifically in the backbone network. This modification aims to improve the accuracy of feature extraction for targets at different scales, significantly reduce the model’s parameters and computational cost, and achieve a lightweight design. The operational process of LDConv is illustrated in Fig. 1.
As shown in Fig. 2a, LDConv first generates initial sampling coordinates for convolutions of arbitrary sizes. For regular convolutions, the sampling grid uses the convolution center as the origin, while for irregular convolutions, the top-left coordinate is adopted as the origin. After defining the origin coordinates, the initial shape of the convolution is proposed by the following Eq. (1):
where \(R\;and\;w\;and{\text{ }}x({P_0}+{P_n})\) represent the generated sampling grid, convolution parameters, and pixel values at corresponding positions, respectively.
We simultaneously establish the initial coordinates of the convolution kernel as \(({P_0}+{P_n}).\) The first step serves to generate sampling coordinates for the convolution kernel on the feature map. As shown in Fig. 1b, in the second step, we obtain the offset corresponding to the convolution kernel through convolution operations. This offset is added to the initial coordinates to generate new sampling coordinates for the convolution. The second step aims to determine the sampling shape for convolutions located at different positions on the feature map. Finally, LDConv acquires features at corresponding positions through interpolation and resampling, then achieves output through reshaping, convolution, normalization, and SiLU activation.
By leveraging a flexible convolution kernel structure and offset design, LDConv effectively adapts to targets of various sizes and shapes, improving the accuracy and efficiency of feature extraction. This approach significantly reduces the model’s parameters and computational cost while enhancing detection accuracy. Considering these characteristics and the need for model lightweighting in this study, we replaced the convolutional layers in the 2nd, 3rd, 4th, and 5th layers of the original YOLOv8, as shown in Fig. 2.
ACMix attention module
In the inspection of transmission lines, ultraviolet (UV) images of insulators often feature complex backgrounds or insulator regions that occupy a relatively small portion of the overall image. When deep learning algorithms are applied to identify discharge spots, the presence of small targets often results in a significant decline in accuracy. Therefore, it is essential to enhance the model’s focus on defect regions, directing more resources toward extracting feature information from these areas.
To address this issue, we incorporated the ACMix hybrid self-attention mechanism16. The underlying principle of ACMix is illustrated in Fig. 3.
As shown in Fig. 3a, the computational process of a standard convolution operation is as follows. Assume the convolution kernel size is \(K \in {R^{{C_{out}} \times {C_{in}} \times k \times k}}\), where k represents the kernel size, and \({C_{in}},{C_{out}}\) are the input and output channel dimensions, respectively. Let the input and output feature maps be represented as tensors \(F \in {R^{{C_{out}} \times {C_{in}} \times k \times k}},G \in {R^{{C_{out}} \times H \times W}}\), where HHH and WWW denote the height and width of the image. The feature tensor corresponding to pixel (i, j) in the input and output feature maps is denoted as \({f_{i,j}} \in {{\text{R}}^{{C_{in}}}},{g_{i,j}} \in {R^{{C_{out}}}}\), respectively. The computation process for standard convolution can then be expressed as Eq. (2):
where \({K_{p,q}} \in {{\text{R}}^{{C_{out}} \times {C_{in}}}},p,q \in \{ 0,1,\ldots,k - 1\}\) represents the kernel weight indexed at position (p, q).
To simplify the standard convolution operation, we introduce a Shift operation, as described in Eq. (3):
With the introduction of the Shift operation, the computation process of standard convolution can be summarized into two stages. In the first stage, the input feature map is linearly projected along the kernel weights at specific positions, equivalent to the operation of a standard 1 × 1 convolution. In the second stage, the projected feature map is shifted according to the kernel positions, followed by aggregation. The overall process is expressed in Eq. (4):
From Eq. (4) and Fig. 3(a), it can be observed that the majority of the computational workload in the convolution operation occurs during the 1 × 1 convolution stage, while the shifting and aggregation are lightweight operations.
Figure 3(b) illustrates the standard computation process of the self-attention mechanism. The output calculation formula for the standard self-attention module can be expressed as Eq. (5):
In this equation, \(W_{q}^{{(l)}},W_{k}^{{(l)}},W_{v}^{{(l)}}\)represent the projection matrices for the query, key, and value, respectively, and \(\parallel\)denotes the concatenation operation of multiple attention heads.
Similar to standard convolution, the computation process of the self-attention mechanism can also be divided into two stages. In the first stage, a 1 × 1 convolution is performed to project the input features into the query, key, and value feature matrices. In the second stage, attention weights are computed, and the value matrix is aggregated. Similar to convolution operations, the main computational load in the self-attention mechanism occurs during the 1 × 1 convolution in the first step.
From the analysis above and Fig. 3a and b, it is evident that the convolution operation and the self-attention mechanism are essentially identical in the 1 × 1 convolution projection of the input feature map. Therefore, we introduce the ACMix hybrid attention mechanism, the structure of which is shown in Fig. 3c. The main process is also divided into two stages. The first stage involves performing three 1 × 1 convolutions on the input feature map to obtain an intermediate feature set containing multiple feature maps. In the second stage, the process splits into two branches:
-
1.
The lower branch, which is the self-attention mechanism branch, aggregates the intermediate features from the 1 × 1 convolution into N groups, each containing three feature maps. These feature maps are then processed using the query, key, and value operations, as in the second step of the self-attention mechanism.
-
2.
The upper branch, which is the convolution operation branch, uses a fully connected layer to generate N groups of \({k^2}\)feature maps, which are then shifted and aggregated through the steps of the convolution operation.
Finally, the outputs from the two branches are summed, effectively combining the convolution layer and the self-attention mechanism.
The introduction of the ACMix method allows for effective focus on target points while incurring minimal loss in model inference speed. We integrate the ACMix module into the Neck-to-Head connection part, as shown in Fig. 2.
Shape-IoU loss function
As a critical component in the detection head of object detection algorithms, the bounding box regression loss plays a significant role in target detection. Compared to earlier versions of the YOLO series, the YOLOv8 algorithm introduces significant improvements in its network structure. However, it does not modify the IoU loss function and still uses the Complete-IoU (CIoU) loss function. The computation formula for CIoU is expressed as Eq. (6).
In this equation, the parameters \(w,h\)represent the width and height of the predicted bounding box, while \({w^{gt}},{h^{gt}}\)represent the width and height of the ground truth bounding box. The parameters \({W^i},{H^i}\)represent the width and height of the intersection area between the predicted bounding box and the ground truth bounding box, respectively. The parameters S represent the areas of the predicted and ground truth bounding boxes, respectively. Additionally, \({\gamma ^2}(b,{b^{gt}})\)denotes the distance between the center points of the predicted and ground truth boxes, and c represents the diagonal distance of the smallest enclosing rectangle that can encompass both boxes.
CIoU, like other commonly used bounding box loss functions, only considers the geometric relationship between the ground truth box and the predicted box, but it ignores the potential impact of the bounding box’s shape and scale on the bounding box regression. Paper17 demonstrated that when the ground truth box is not a square but a rectangle, and its offset and shape offset are identical and not all zero, the dimensions and shape of the predicted and ground truth boxes can lead to differences in the IoU value. For combinations of predicted and ground truth boxes with the same scale, the IoU for smaller-scale combinations is most significantly affected by the ground truth box.
Since the ultraviolet discharge images we are working with often contain irregularly shaped annotation boxes for discharge spots, the IoU is heavily influenced by the shape. To address this IoU discrepancy, we choose to introduce Shape-IoU17 to replace the original CIoU loss function. The computation formula for Shape-IoU is expressed as Eq. (7):
where scale is the scale factor, which is related to the scale of the labeled targets in the dataset, ww and hh are the weight coefficients in the horizontal and vertical directions respectively, whose values are closely related to the shape of the Ground Truth box. Due to the introduction of scale and the concepts of ww and hh, the IoU will take the size and shape concepts of the target and the labeled box into consideration when calculating, which can solve the problem that the traditional IoU is greatly affected by the shape.
Compared to the original CIoU loss function, the Shape-IoU method improves the model’s recognition of irregularly shaped or small-sized targets by focusing on the shape and scale of the predicted box when calculating the IoU loss.
Experiment and result analysis
Model metrics
To conduct a qualitative analysis and evaluation of the object detection algorithm model, this paper uses frames per second (FPS) commonly used in videos to evaluate the detection speed of the algorithm, The FPS we use the average of multiple experiments and video streaming detection throughout the whole process. For the model’s accuracy, the mean Average Precision (mAP) is used, where mAP is calculated using mAP@0.5, meaning the IoU threshold is set to 50%.
The definition of mAP is expressed in Eq. (8):
Insulator discharge UV spot dataset
Currently, there is no high-quality, large-scale publicly available dataset for research on ultraviolet discharge images. Therefore, in training deep learning models, it is necessary to construct a training dataset from scratch.
To obtain the ultraviolet discharge spot images of insulators required for training, this paper built a UV test platform for insulators. The experimental imaging equipment used was the CoroCAM504 ultraviolet camera. The insulators were placed in an artificially humidified environment with humidity up to 95%. The fog chamber lens used specialty glass with more than 95% ultraviolet transmittance.
The experiment selected porcelain insulators in an 8-piece series. The surface contamination was artificially adjusted to 0.2 mg/cm2, and different concentrations of salt-contaminated materials were applied to simulate light, moderate, and severe pollution. The equivalent salt deposit density (ESDD) was set to 0.1 mg/cm2, 0.2 mg/cm2, and 0.4 mg/cm2, respectively. After the contamination of the insulators, a constant voltage was applied, and ultraviolet discharge videos were recorded using an external monitoring camera while simultaneously collecting leakage current data. Subsequently, static images were extracted from the videos at a rate of one frame per second, with each image annotated with the corresponding leakage current value. This resulted in the creation of an initial dataset containing 2695 ultraviolet discharge images.
Based on this dataset, the images were categorized into the following three classes according to the spot area ratio and leakage current peak value of the ultraviolet images.
The labeling of discharge severity was based on the combination of spot area and leakage current peak value. When the spot area accounted for less than 20% of the total insulator area, and the leakage current peak was below 50 mA, it was defined as light discharge. If the spot area ratio was between 20% and 80%, and the leakage current peak was between 50 and 150 mA, it was classified as moderate discharge. When the spot area ratio exceeded 80%, and the leakage current peak was higher than 150 mA, it was considered severe discharge.
After labeling, the initial dataset contained 1556 light discharge images, 762 moderate discharge images, and 377 severe discharge images. However, due to the noticeable imbalance in the sample distribution, directly using this dataset might result in difficulties in feature extraction or overfitting during model training. Therefore, to enhance the model’s robustness and generalization ability, this paper applied data augmentation methods such as rotation and cropping to expand the dataset. The final enhanced dataset is named the Insulator Discharge UV Spot DataSet (IDUVSD), and its data statistics are shown in Table 1.
Experimental environment, hyperparameter settings and training results
Since the algorithm model designed in this paper needs to be considered for deployment in the edge computing module of field fiber cameras, high-performance training servers were used for training, and medium-performance edge devices were used for testing. The experimental environment in this paper is shown in Table 2.
Model training requires the manual setting of hyperparameters. The hyperparameters used in this study are shown in Table 3.
To prevent the issue of incomplete model convergence due to insufficient training epochs, a training batch of 2000 iterations was set, and the training was terminated if there was no more than a 0.5% improvement in mAP after 200 epochs.
The RDIDSNet model proposed in this paper was trained and tested on field discharge ultraviolet images to assess the severity of the discharges. The test image for the severity evaluation is shown in Fig. 4.
Ablation experiment
To analyze the effectiveness of the modules introduced in the proposed algorithm model for model lightweighting and accuracy improvement, experiments were conducted under the same deployment devices, and training datasets. The results are shown in Table 4.
As shown in Table 4, the original YOLOv8 network achieves a detection speed of 41 frames/s with an mAP@0.5 of 68.2%.
Network-1 replaces part of the feature extraction convolution in the backbone network with LDConv. Since LDConv allows for the flexible selection of kernel size and number, it significantly enhances the feature extraction capability of Network-1 while notably reducing the detection speed. Network-1 saw a 2.1% improvement in mAP and a 26-frame increase in speed.
Building upon Network-1, Network-2 introduces the ACMix attention mechanism, which combines convolutional layers with self-attention mechanisms. This fusion improves the model’s focus on the target with minimal computational cost, significantly enhancing the detection accuracy. The mAP increased from 70.3 to 75.2%, though the detection speed decreased by 3 frames/s due to the inevitable increase in overall model complexity.
Finally, Network-4, or RDIDSNet, further improves upon Network-3. Shape-IoU optimizes for datasets with complex shapes, leading to a significant boost in detection accuracy. The model trained on this dataset demonstrates stronger robustness.
The ablation study results indicate that the optimized YOLOv8 reaches a speed of 61 frames/s while improving detection accuracy by 9.9%, strongly validating the effectiveness of the proposed improvements to the YOLOv8 algorithm.
Algorithm comparison experiment
To further demonstrate the advantages of the RDIDSNet al.gorithm, several commonly used object detection models in the engineering field were selected for comparison, including Faster-RCNN18, DETR19, YOLOv5, YOLOv6 20, YOLOv7 21, and YOLOv8 6. These models were trained and performance-tested on the IDUVSD dataset. The experiments were conducted under the same hardware environment, and the results are shown in Table 5.
Based on Table 5, although Faster-RCNN achieves slightly higher accuracy compared to DETR and YOLOv5, its inference speed is limited to just 2 frames per second (fps) due to its two-stage architecture. DETR shows a slight improvement in speed over Faster-RCNN but still falls short in terms of frame rate, with its detection accuracy only reaching 59.9%, which is insufficient for practical use. YOLOv5 strikes a balance between detection speed and accuracy, offering an inference rate of 23 fps and a detection accuracy of 66.2%, but it still doesn’t meet the required performance. YOLOv6, YOLOv7, and YOLOv8 perform well on general datasets like COCO and VOC, but their effectiveness for insulator discharge detection is lacking. Among them, YOLOv7 shows the highest detection accuracy, but its inference speed is only 6 fps. In contrast, the RDIDSNet algorithm proposed in this paper excels in discharge detection tasks, achieving significantly higher accuracy than other models and is well-suited to meet the application needs for evaluating insulator discharge severity.
Comparative experiments with similar algorithms
To compare the performance of the proposed RDIDSNet algorithm with similar algorithms for discharge defect detection or power-related image detection, two related algorithms were selected and trained on the IDUVSD dataset. The experiments were conducted on the same test equipment, and the results are shown in Table 6.
From the data presented in Table 6, it is clear that although Network-1 from the literature achieves a similar inference speed to RDIDSNet at 55 frames per second, its detection accuracy is only 59.2%, which falls short of meeting the necessary requirements for discharge defect detection. On the other hand, the proposed RDIDSNet algorithm not only achieves a higher inference speed of 61 frames per second but also reaches a significantly better recognition accuracy of 78.1%, making it well-suited for on-site evaluation of insulator discharge severity.
This demonstrates that RDIDSNet provides an effective balance between detection speed and accuracy, addressing the demands of real-time monitoring and precise defect analysis in the power industry.
Conclusions
This paper proposes a rapid detection algorithm for insulator discharge severity evaluation based on the improved YOLOv8 algorithm, addressing the need for on-site assessment of insulator discharge severity. The main contributions are as follows:
-
1.
The introduction of LDConv to improve the convolutional layers of the YOLOv8 algorithm, significantly reducing the model’s overall parameter count and computational load while effectively improving detection accuracy. Next, the ACMix attention mechanism is introduced, achieving target focus with minimal performance cost, effectively solving issues of poor localization ability and low detection accuracy. Finally, the model’s loss function was modified by replacing the CIoU loss function with the Shape-IoU loss function, effectively addressing the interference of bounding box shape and scale due to irregular insulator discharge UV spot shapes.
-
2.
A UV discharge testing platform was built for capturing UV discharge images, and the images were labeled and augmented. Ultimately, a dataset consisting of 4404 insulator discharge UV images, categorized into three classes, was constructed.
-
3.
Experimental results demonstrate that the proposed algorithm outperforms the original YOLOv8 algorithm in both inference speed and detection accuracy. With a detection accuracy exceeding 75%, the detection rate achieved 61 frames/s. Furthermore, comparative experiments confirm that the proposed method outperforms current commonly used object detection algorithms and similar recognition algorithms.
Although our proposed RDIDSNet has achieved better results than currently commonly used object detection algorithms and similar recognition algorithms, it still has some shortcomings, and more research is needed to improve it in the future:
-
1.
The training of the model requires a large amount of data, but in practical applications, the amount of data is often too small to complete the training, so it is necessary to carry out improvement research on small-sample training in the later stage.
-
2.
At present, the model has a low recognition accuracy for discharge images between the two states, so it is necessary to further study the subdivision method for the classification of discharge severity images and improve the algorithm to achieve more accurate detection accuracy.
Data availability
Due to the need for confidentiality on the part of the article’s funders, the data presented in this study are available upon request from the corresponding author.
References
Guo, J., Zhao, Y., Wang, Z. & Ding, L. Recognition method of local discharge patterns of typical defects in pin-type insulators based on LMD and LSTM. South. Power Grid Technol. 15(8), 95–105. https://doi.org/10.13648/j.cnki.issn1674-0629.2021.08.012 (2021).
Tan, X., Chen, R., Ding, W. & Zhang, G. Non-destructive detection of electrical insulator discharges based on improved convolutional neural networks. Autom. Instrum. 38(4), 88–91. https://doi.org/10.19557/j.cnki.1001-9944.2023.04.018 (2023).
Wang, S., Dong, X., Wang, X., Jin, C., Sun, K. & Lü, F. Evaluation of discharge severity in suspension insulators based on improved SSD algorithm and UV imaging. J. North China Electr. Power Univ. (Nat. Sci. Edn.). 50(5), 35–44 (2023).
Lü, F., Niu, L., Wang, S. & Chu, Y. Evaluation of discharge severity in porcelain suspension insulators based on UV imaging and improved YOLOv3. High. Volt. Technol. 47(2), 377–386. https://doi.org/10.13336/j.1003-6520.hve.20200674 (2021).
Yang, Y., Geng, S., Cheng, C., Yang, X., Wu, P., Han, X. & Zhang, H. An edge algorithm for assessing the severity of insulator discharges using a lightweight improved YOLOv8. J. Electr. Eng. Technol. 20(1), 807–816. https://doi.org/10.1007/s42835-024-02021-4 (2025).
Varghese, R. & Sambath, M. YOLOv8: A novel object detection algorithm with enhanced performance and robustness. In International Conference on Advances in Data Engineering and Intelligent Computing Systems (ADICS) 1–6. https://doi.org/10.1109/ADICS58448.2024.10533619 (2024).
Yao, J. & Kowal, J. A. Multi-scale data-driven framework for online state of charge estimation of lithium-ion batteries with a novel public drive cycle dataset. J. Energy Storage 107, 114888. https://doi.org/10.1016/j.est.2024.114888 (2025).
Tan, M., Pang, R. & Le, Q. V. Efficientdet: Scalable and efficient object detection 10781–10790 (2020).
Feng, C., Zhong, Y., Gao, Y., Scott, M. R. & Huang, W. TOOD: Task-aligned one-stage object detection. IEEE Comput. Soc. 3490–3499. https://doi.org/10.1109/ICCV48922.2021.00349 (2021).
Li, X., Wang, W., Wu, L., Chen, S., Hu, X., Li, J., Tang, J. & Yang, J. Generalized focal loss: Learning qualified and distributed bounding boxes for dense object detection. In Advances in Neural Information Processing Systems Vol. 33, 21002–21012 (Curran Associates, Inc., 2020).
Zheng, Z., Wang, P., Liu, W., Li, J., Ye, R. & Ren, D. Distance-IoU loss: faster and better learning for bounding box regression. Proc. AAAI Conf. Artif. Intell. 34(07), 12993–13000. https://doi.org/10.1609/aaai.v34i07.6999 (2020).
Pei, S., Zhang, H., Zhu, Y. & Hu, C. Lightweight transmission line defect identification method based on OFN network and distillation method. IET Image Proc. 18(12), 3518–3529. https://doi.org/10.1049/ipr2.13191 (2024).
Hu, C., Pei, S., Liu, Y., Yang, W., Yang, R., Zhang, X. & Liu, H. A real-time defect detection method for transmission line edge devices based on LEE-YOLOv7. High Volt. Technol. 50(11), 5047–5057. https://doi.org/10.13336/j.1003-6520.hve.20230945 (2024).
Pei, S., Zhang, X., Hu, C., Yang, W. & Liu, Y. A cross-environment transmission line defect recognition method based on ER-YOLO algorithm. Trans. China Electrotech. Soc. 39(9), 2825–2840. https://doi.org/10.19595/j.cnki.1000-6753.tces.232073 (2024).
Zhang, X., Song, Y., Song, T., Yang, D., Ye, Y., Zhou, J. & Zhang, L. Linear deformable Convolution for improving convolutional neural networks. Image Vis. Comput. 149, 105190. https://doi.org/10.1016/j.imavis.2024.105190 (2024).
Pan, X., Ge, C., Lu, R., Song, S., Chen, G., Huang, Z. & Huang, G. On the integration of self-attention and convolution 815–825. (2022).
Zhang, H. & Zhang, S. Shape-IoU more accurate metric considering bounding box shape and scale (2024). https://doi.org/10.48550/arXiv.2312.17663
Ren, S., He, K., Girshick, R. & Sun, J. Faster R-C-N-N: Towards real-time object detection with region proposal networks. IEEE Trans. Pattern Anal. Mach. Intell. 39(6), 1137–1149. https://doi.org/10.1109/TPAMI.2016.2577031 (2017).
Carion, N., Massa, F., Synnaeve, G., Usunier, N., Kirillov, A. & Zagoruyko, S. End-to-end object detection with transformers. In Computer Vision—ECCV 2020; (eds Vedaldi, A., Bischof, H., Brox, T. & Frahm, J. M.) 213–229 (Springer International Publishing, Cham, 2020). https://doi.org/10.1007/978-3-030-58452-8_13.
Li, C., Li, L., Jiang, H., Weng, K., Geng, Y., Li, L., Ke, Z., Li, Q., Cheng, M., Nie, W., Li, Y., Zhang, B., Liang, Y., Zhou, L., Xu, X., Chu, X., Wei, X., Wei, X. YOLOv6: A single-stage object detection framework for industrial applications. https://doi.org/10.48550/arXiv.2209.02976 (2022).
Wang, C. Y., Bochkovskiy, A. & Liao, H. Y. M. YOLOv7: Trainable Bag-of-Freebies Sets New State-of-the-Art for Real- 7464–7475 (Time Object Detectors, 2023).
Haoyu, L., Shuguo, G., Xu, T., Qian, Z., Meng, G., Keyu, L., Shaotong, P. & Weiqi, W. Transformer abnormal heat accurate identification method based on AHIPDNet. Sci. Rep. 14(1), 29456. https://doi.org/10.1038/s41598-024-81286-1 (2024).
Funding
This research was funded by State Grid Hebei Electric Power Co., Ltd, Ultra High Voltage Branch, Grant No. SGHEJX00YJJS2250153.
Author information
Authors and Affiliations
Contributions
Conceptualization, Keyu Li; Data curation, Keyu Li and Yanhui Meng; Funding acquisition, Cheng Chi, Yanhui Meng, Yang Yang and Jining Zhao; Methodology, Cheng Chi, Keyu Li and Yang Yang; Project administration, Cheng Chi, Yanhui Meng and Shaotong Pei; Software, Cheng Chi; Su-pervision, Cheng Chi; Validation, Yang Yang; Visualization, Haosen Sun; Writing—original draft, Cheng Chi and Keyu Li; Writing—review and editing, Yanhui Meng, Jining Zhao, Shaotong Pei and Haosen Sun.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Chi, C., Keyu, L., Meng, Y. et al. Insulator discharge severity assessment algorithm based on RDIDSNet. Sci Rep 15, 11934 (2025). https://doi.org/10.1038/s41598-025-97010-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-025-97010-6