Abstract
Modern power distribution network incorporates distributed generation (DG) for numerous benefits. However, the incorporation creates numerous challenges in energy management and to handle the challenges it requires advanced optimization techniques for an effective operation of the network. Unlike traditional methods such as Genetic Algorithm (GA), Particle Swarm Optimization (PSO), and standard Crow Search Algorithm (CSA), which suffer from premature convergence and limited adaptability to real-time variations, Reinforcement Learning Enhanced Crow Search Algorithm (RL-CSA) which is proposed in this research work solves network reconfiguration optimization problem and minimize energy losses. Unlike conventional heuristic methods, which follow predefined search patterns, RL-CSA dynamically refines its search trajectory based on real-time feedback, ensuring superior convergence speed and global search efficiency. The novel RL-CSA enables real-time adaptability and intelligent optimization for energy loss reduction in distributed networks. The proposed model validation is performed on the IEEE 33 and 69 Bus test systems considering diverse performance metrics such as power loss reduction, voltage stability, execution time, utilization efficiency for DG deployment, and energy cost minimization. Comparative results show that RL-CSA achieves a 78% reduction in energy losses, limiting power loss to 5 kW (IEEE 33-Bus) and 8 kW (IEEE 69-Bus) whereas traditional models converge at higher loss levels. The execution time is optimized to 1.4 s (IEEE 33-Bus) and 1.8 s (IEEE 69-Bus), significantly faster than GA, PSO, and CSA, making RL-CSA more efficient for real-time power distribution applications. By balancing exploration-exploitation using CSA while adapting search parameters through reinforcement learning, RL-CSA ensures scalability, improved DG utilization (98%), and better voltage stability (< 0.005 p.u.), making it a robust and intelligent alternative for modern smart grid optimization.
Similar content being viewed by others
Introduction
Background
Energy distribution network (EDN) management is a key task in current power systems due to the ever-increasing distributed generation (DG) sources such as solar photovoltaic systems, wind turbines and micro hydro plants1. The energy loss optimization in distributed networks is the problem of minimizing power dissipated due to such factors as transmission losses, poor load balancing, and voltage regulation inefficiencies2. These losses increase the power distribution system operational cost and also decrease its total efficiency. Optimizing energy loss is a must to achieve sustainable energy system3 and it ensures grid stability, power quality and lower carbon footprints. To reduce losses and improve system reliability, effective strategies must take account of real time power flow control and adaptive grid configurations of which variation of dynamic load is also taken into consideration4,5. Even with advances in energy management, a number of practical limitations still exist in the energy loss optimization in distributed networks. Renewable energy sources have a stochastic nature causing the power generation to exhibit an unpredictable fluctuation which results in voltage instability and frequency deviation6. Furthermore, DG units are not easily integrated into the existing distribution networks due to the fact that they were not originally designed for bidirectional power flow, which can cause overvoltage or under-voltage issues7. Also, harmonics and reactive power imbalances add to the energy dissipation8. Additionally, static configurations are used in conventional control mechanisms, which are not effective to respond to the real time variations in load demand and generation9. Complexity issues for large scale distribution networks also present significant challenge in real time optimization, as such real time decisions must be made using multi objective constraints with low latency and advances algorithms.
Traditional optimization methodologies
There have been developed various techniques of energy loss optimization in distributed networks, which can be divided into heuristic, analytical, and artificial intelligence (AI) based methods10. The optimization problems in power systems have been often solved by using analytical methods, e.g. linear programming (LP) and mixed integer nonlinear programming (MINLP). However, most of these methods offer exact solutions but offer low scalability for large networks with high renewable integration11. Traditional optimization techniques for energy loss minimization in distributed networks exhibit several critical limitations, which this study aims to address. Heuristic-based algorithms such as Genetic Algorithm (GA), Particle Swarm Optimization (PSO), and Crow Search Algorithm (CSA), though widely used, struggle with premature convergence, often getting trapped in local optima, leading to suboptimal power loss reduction12. These methods also require extensive parameter tuning, reducing their practicality for real-time grid operations where dynamic adaptability is essential. Analytical approaches, including Linear Programming (LP) and Mixed-Integer Nonlinear Programming (MINLP), provide exact solutions but fail to scale efficiently in large, complex networks with high renewable penetration. Hybrid metaheuristic models improve search efficiency but remain limited by their static control mechanisms, preventing them from continuously adapting to real-time variations in power flow and load demand. AI-based methods such as Reinforcement Learning (RL) offer adaptive learning capabilities but suffer from high computational costs and long convergence times, making them impractical for rapid decision-making in power distribution systems. Furthermore, existing optimization frameworks lack an integrated learning mechanism that can effectively balance exploration and exploitation while dynamically optimizing Distributed Generation (DG) allocation, network reconfiguration, and voltage regulation.
Recent AI based methodologies
In recent years, besides ANNs, AI based optimization approaches especially machine learning, deep learning and reinforcement learning have attracted more and more attention due to their capability to learn adaptive control policies from historical data13,14,15,16. The models based on reinforcement learning (RL) can optimize the energy loss by reconfiguring the control parameters in real time in accordance with the network conditions. Some demand response management and optimal power dispatch techniques are applied, including techniques like Proximal Policy Optimization (PPO), Deep Q-Networks (DQN), and actor critic methods. However, the training times and computational resources needed to converge are high for the RL methods. Limitations have been overcome by hybrid approaches using heuristic search with RL. Hybrid models combine AI based decision making with heuristic optimization to achieve high adaptability within computational efficiency. Also, existing optimization frameworks lack an integrated learning mechanism that can effectively balance exploration and exploitation while dynamically optimizing Distributed Generation (DG) allocation, network reconfiguration, and voltage regulation. This brings an open research challenge and requires a scalable and robust optimization method that balances real time adaptability, low computational cost and good global search efficiency.
Research objective
The major contribution of this research is to fill the gaps in current energy loss optimization by presenting a Reinforcement Learning Enhanced Crow Search Algorithm (RL-CSA). The most important feature of this study is to establish an intelligent optimization framework subject to network variations, such that power dissipation is minimized and voltage stability is maintained. The motivation to integrate RL with CSA arises to find a way to optimally explore the search space with learning from real time network feedback. CSA offers an excellent exploration exploitation trade-off while RL allows continuous learning and policy improvement in decision making. The RL-CSA model proposed here is aimed at devising a DG allocation, network topology reconfiguration, and power flow balancing process dynamically to achieve sustainable and resilient energy distribution.
Research novelty
The research novelty is the integration of reinforcement learning with a metaheuristic search process, allowing for intelligent and adaptive decision-making in power distribution networks. Unlike traditional CSA implementations, which rely on predefined movement strategies, the RL-CSA framework dynamically updates the optimization trajectory based on learned policies, improving convergence speed and global search effectiveness. The proposed RL-CSA significantly differs from existing hybrid AI-based optimization techniques by integrating adaptive learning into heuristic search, making it more efficient for dynamic energy loss optimization in power networks. Unlike traditional hybrid models which rely on fixed control parameters and require extensive training, RL-CSA continuously refines its search strategy through real-time feedback. This eliminates premature convergence issues, ensuring faster adaptation to fluctuating power demands and renewable generation variations. Additionally, RL-CSA optimizes both exploration and exploitation dynamically, unlike standard metaheuristic hybrids that struggle with balancing these aspects. Its superior performance in power loss reduction, DG utilization, voltage stability, and faster convergence proves its efficiency over conventional AI-heuristic combinations. Also, the incorporation of adaptive reinforcement learning module refines decision parameters in real-time, ensuring robust performance under varying grid conditions. By utilizing a hybrid approach, this study bridges the gap between static heuristic models and fully AI-driven methods, offering a practical yet innovative solution for energy loss reduction in distributed networks.
Research contributions
The research work contributions are summarized as follows.
-
1.
Developed of a Novel RL-CSA integrating reinforcement learning with Crow Search Algorithm to enhance the search efficiency and adaptability in real-time power distribution networks. Through the novel approach the Dynamic Reconfiguration of Distributed Networks is attained by continuous optimization of DG placement and network topology to minimize energy losses.
-
2.
Presented a detailed analysis on IEEE 33 and 69-bus systems to demonstrate superior performance of proposed model. The proposed RL-CSA model accelerates convergence while maintaining accuracy, making it suitable for large-scale distributed energy systems.
-
3.
Presented a detailed comparative analysis with existing methodologies like Cuckoo search algorithm (CSA), Genetic Algorithm (GA), and Particle Swarm optimization (PSO) to validate the proposed model superior performance.
The remainder of this paper is structured as follows: Section “Related works” provides a detailed literature review and comparison of existing techniques. Section “Proposed work” presents the proposed RL-CSA methodology, including its learning framework and optimization strategy. Section “Results and discussion” describes the experimental setup, evaluation metrics, and test system parameters. Section “Conclusion” concludes the study with recommendations for future research directions.
Problem statement
The rapid integration of distributed generation (DG) into modern power networks has introduced significant challenges in energy loss optimization, voltage regulation, and real-time network reconfiguration. Traditional heuristic and metaheuristic approaches, often suffer from premature convergence, poor adaptability to dynamic grid variations, and high computational complexity, making them unsuitable for large-scale power distribution networks. Analytical methods like Mixed-Integer Nonlinear Programming (MINLP) provide exact solutions but lack scalability and struggle with real-time adaptability. AI-based methods, including Reinforcement Learning (RL), offer dynamic learning capabilities but face limitations in terms of training complexity and computational overhead. To address these gaps, this research presents the Reinforcement Learning-Enhanced Crow Search Algorithm (RL-CSA), a hybrid optimization framework that dynamically refines search trajectories, optimizes DG allocation, and enhances power distribution efficiency while maintaining low execution time and superior solution accuracy.
Related works
In this section, some of the recent research works on optimizing power distribution network configuration are analyzed and summary is provided. Some of the metaheuristic optimization techniques used in power distribution network (PDN) reconfiguration are presented in17. Traditional optimization techniques such as linear programming or deterministic solutions tend to fail when a problem has complex and nonlinear constraints present that are typical in PDNR. In order to address these challenges, several heuristic and metaheuristic algorithms addressed these challenges such as Grasshopper optimization algorithm (GOA), Particle Swarm optimization (PSO), and Equilibrium optimizer (EO) among others. This study reveals that EO has a superior balance between exploration and exploitation that makes it converge well to the optimal solutions. Additionally, the effectiveness of existing methods is related to their process of global to local search through PSO and GOA, which might lead them sometimes into the local optima, while the optima are always addressed globally with lower computational cost by EO. Experimental analysis is performed and shows that EO is the best performance in terms of accuracy and convergence speed, which is an efficient solution for reconfiguration of PDN.
In18 Chaotic Search Group Algorithm (CSGA) is used for network reconfiguration and DG allocation. Traditional optimization methods are generally used to tackle the problem however traditional models are confronted with premature convergence and the trapping of local optima to obtain performance suboptimal. To cope with the above problems, CSGA combines the CLS strategy with the original Search Group Algorithm (SGA) and enhances the efficiency and convergence speed of search. It is validated on IEEE 33, 69, 84, and 118 bus radial distribution networks (RDNs) across different load levels. Results of the experimental results show considerable power loss reduction over conventional optimization techniques. Yet, key to algorithm limitations is its dependency on parameter tuning and its expanded computational complexity with larger scale networks.
In19, Radiality Maintenance Algorithm (RMA) is used to help improve the efficiency of metaheuristic approaches in network reconfiguration with battery storage integration. In the presented RMA, junction nodes and a selection set are used to generate and maintain only radial topologies during optimization. The IEEE 33 Bus test system is reconfigured with RMA using Accelerated PSO (APSO) to reduce standard deviation by 27.3% and compute in 1.6 s. The experimental results show that power loss reduction and system stability are significantly improved with complexity reduction in verifying radiality constraints in large scale networks. However, parameter sensitivity and required fine-tuned configurations of the metaheuristic are challenges in particular for dynamically changing distribution networks.
The Selective Bat Algorithm (SBAT) presented in20 considers voltage and current unbalance indexes under variable demand for Distribution Network Reconfiguration. Conventional methods often assume balanced systems with fixed power loads, limiting their applicability in real-world networks. To overcome these constraints, SBAT is employed, integrating a sigmoid function for discrete variable selection and a selective search mechanism for optimal switch reconfiguration. The methodology is validated using IEEE 19, 25, 33, and 69-Bus test systems, with simulations conducted via EPRI-OpenDSS. Experimental results better reduction in real power losses for IEEE 33 and 69 systems, respectively, and improved voltage stability. Moreover, SBAT outperforms SPSO and SHS in convergence efficiency and computational time. However, limitations include parameter sensitivity and increased computational complexity for large-scale networks.
A Chaotic Golden Flower Algorithm (CGFA) is presented in21 for optimizing distribution network reconfiguration in smart city power systems. The presented CGFA hybridizes the Flower Pollination Algorithm (FPA) with the Golden Search Algorithm (GSA) to enhance global search capability while reducing local optima entrapment. Experimental validation is conducted on IEEE 33, 69, 119-bus systems, and an Indian 52-bus smart city network, incorporating energy storage systems (ESS) with DG. It is shown to reduce power loss better and at a lower computational cost than the existing methods. However, parameter tuning is required for effectiveness and scalability for large networks is an open problem.
In22, a metaheuristic technique for simultaneous DG allocation and network reconfiguration (NR) in PDN is specifically termed as Geometric Mean Optimization (GMO). Dynamic placement of DG is achieved using the proposed method by coupling GMO with Power Loss Sensitivity Index (PLSI) to provide voltage regulation while maintaining low power losses. The methodology is tested on IEEE 33 and 69-bus distribution networks under different loading levels and results show significant reduction in voltage deviation (VD) and total active power loss (TAPL). Results show that the performance of simultaneous NR and DG allocation with OPF is the best, and comparable to conventional methods, reducing TAPL by 94.96% and 97.92% for IEEE 33 and 69 bus respectively. Although parameter tuning and computational complexity are still crucial limitations.
Tangent Golden Flower Pollination Algorithm (TGFPA) is presented in23 for optimizing NR and DG placement in PDN. The TGFPA integrates the Golden Section Search Algorithm (GSA) and Tangent Flight Algorithm (TFA) within the Flower Pollination Algorithm (FPA) to enhance global search exploration and local exploitation. The approach is validated on IEEE 33, 69, 119-bus systems and an Indian 52-bus system, demonstrating significant reductions in power loss (PL), voltage deviation, and computational time. Experimental results reveal that TGFPA reduces power losses by up to 27.3% in the IEEE 33-bus system while maintaining efficient DG utilization. However, parameter sensitivity and scalability for real-time applications remain key challenges. Future research could explore hybrid AI-based methods to enhance real-time adaptability and optimization under dynamic load conditions.
The Jellyfish Search Algorithm (JFS) is presented in24 for optimal distribution network reconfiguration (DNR) to enhance operational reliability in power distribution systems. The presented optimization model has the ability to balance exploration and exploitation in a dynamic search space inspired by the behavioral patterns of jellyfish in nature. The methodology is validated on an IEEE 33-node distribution network, where three reliability indices—SAIUI (System Average Interruption Unavailability Index), SAIFI (System Average Interruption Frequency Index), and TENS (Total Energy Not Supplied) are optimized. Experimental results show improvements of 36.44%, 34.11%, and 33.35%, respectively, compared to initial conditions, demonstrating the effectiveness of JFS over conventional swarm optimization models. However, limitations include parameter sensitivity and computational overhead for larger networks.
Iterative Branch Exchange (IBE) and Clustering Technique is combinedly presented in25 for Distribution Network Reconfiguration (DNR) to minimize power losses and improve voltage profiles. Traditional optimization algorithms often face scalability challenges in large-scale networks due to their high computational complexity. The proposed IBE method integrates evolutionary metaheuristics with clustering analysis, reducing the search space and improving solution feasibility. The methodology is validated on IEEE 33, 70, 84, and 136-bus networks, as well as real-world cases from CEMIG-D, demonstrating substantial reductions in power losses and computational effort. Experimental results indicate that the proposed method outperforms traditional metaheuristics by achieving loss reductions with fewer power flow runs, significantly enhancing computational efficiency. However, the study highlights limitations, such as dependency on heuristic rule selection and sensitivity to initial conditions, which may affect solution robustness.
The Grey Wolf Optimization (GWO) algorithm presented in26 for optimal Distribution Network Reconfiguration (DNR) and DG allocation enhances power system efficiency thorough its optimal solution. The presented GWO algorithm utilize its hierarchical leadership structure and provides adaptive exploration-exploitation balance. The study evaluates multiple scenarios under voltage and current constraints on IEEE 33, 69, and 118-bus test systems, demonstrating a 63.13%, 56.19%, and 34.27% active power loss (APL) reduction, respectively, with DNR alone. When integrating DG allocation, APL reductions improve to 69.61%, 82.09%, and 36.08%, confirming the superiority of the proposed approach and its strong performance, GWO’s parameter dependency and computational overhead for larger networks are noted as challenges.
An Improved Salp Swarm Algorithm (ISSA) is presented in27 for optimal placement of photovoltaic panels (PV) and wind turbines (WT) with radial distribution network reconfiguration (DNR) to enhance efficiency and reliability. The presented ISSA integrates Differential Evolution (DE) operators with SSA to improve global search capability and convergence speed. The experimentations is performed using IEEE 33- and 69-bus distribution networks under various renewable energy allocation and reconfiguration scenarios. Simulation results indicate that ISSA achieves higher net savings, lower power loss costs, and improved reliability compared to SSA and other conventional methods. Moreover, ISSA selects the best location, size and power factor of renewable sources that guarantee network radiality and operational constraints. However, the method is computationally complex and sensitive to its initial parameters.
A combination of Simulated Annealing (SA) and Minimum Spanning Tree (MST) algorithm is presented in28 for smart distribution network reconfiguration (DNR) to optimize power loss reduction and economic cost minimization. The presented model utilizes SA and MST separately to determine the optimal shunt capacitor placement DG allocation, and on-load tap changer (OLTC) settings. The methodology is tested on the IEEE 69-bus network, incorporating Gauss and Weibull probability models to represent solar and wind power generation, as well as real one-year load measurement data from a substation in Belgrade, Serbia. Results confirm that the proposed approach provides a near-optimal solution over a wide time range, ensuring voltage stability, feeder capacity constraints, and economic feasibility. However, computational complexity and sensitivity to stochastic load variations remain challenges.
An Enhanced Jellyfish Search Optimizer (EJSO) is presented in29 for energy management in multi-microgrid (MMG) systems integrating photovoltaic, wind, and biomass units while accounting for uncertainty in renewable energy sources. The proposed EJSO incorporates Weibull Flight Motion (WFM) and Fitness Distance Balance (FDB) to overcome stagnation issues observed in the standard Jellyfish Search Optimizer (JSO). Experimental evaluations conducted on the IEEE 85-bus system demonstrated superiority in reducing operational costs and enhancing voltage stability over existing Sand Cat Swarm Optimization, Dandelion Optimizer, and Whale Optimization Algorithm. However, the model’s reliance on predefined parameter tuning and increased computational overhead limits the model exploration ability.
A Modified Capuchin Search Algorithm (MCapSA) is presented in30 to optimize energy management in multi-microgrid (MMG) systems, incorporating photovoltaic (PV) and wind turbine (WT) units under uncertain conditions. MCapSA enhances the original Capuchin Search Algorithm using quasi-oppositional-based learning, Levy flight distribution, and prairie dog optimization for improved convergence. Experimental results on IEEE 33-bus and 69-bus MMGs demonstrated that MCapSA effectively reduces costs while improving voltage stability.
The Horned Lizard Optimization Algorithm (HLOA) presented in31 optimize distribution networks by integrating photovoltaic systems, Distribution Static Compensators (D-STATCOMs), and network reconfiguration. The model incorporates Monte Carlo Simulation (MCS) and Scenario Reduction Algorithm (SRA) to address uncertainties in solar radiation, temperature, and load demand. Experimental validation on the IEEE 33-bus network demonstrated significant improvements in terms of reduced operational costs, real power losses and voltage deviations. However, the HLOA doesn’t have energy storage integration and lags in demand response strategies which limits its adaptability for real-time grid stability enhancements.
The Modified Artificial Rabbit Optimization (MARO) algorithm presented in32 optimizes stochastic energy management in grid-connected microgrids, incorporating microturbines, fuel cells, photovoltaic systems, wind turbines, and battery storage. The MARO enhances the standard Artificial Rabbit Optimization (ARO) by integrating Fitness Distance Balance (FDB), a Prairie Dog Optimization (PDO) exploitation mechanism, and Quasi-Opposite-Based Learning (QOBL) to improve exploration and convergence. Experimental validation using a case study in Wenzhou, China, demonstrated that MARO significantly reduced operational costs while effectively managing system uncertainties through Monte Carlo Simulation and probabilistic modeling.
Research gap
The complete summary of literature review is presented in Table 1. The review of existing literature highlights several critical research gaps in distribution network reconfiguration (DNR) and DG allocation that justify the need for the proposed RL-CSA approach. Many metaheuristic techniques, including PSO, GA, GWO, and SSA, struggle with premature convergence and local optima trapping, leading to suboptimal power loss reduction and voltage stability improvements. While some recent algorithms, such as CSGA, CGFA, and TGFPA, enhance exploration-exploitation balance, they still face high computational complexity and sensitivity to parameter tuning, making them less scalable for real-time applications. Additionally, hybrid approaches like ISSA and SBAT incorporate improvements but lack adaptive learning mechanisms to dynamically optimize network configurations under fluctuating demand and renewable energy penetration. Furthermore, existing models fail to integrate reinforcement learning, which can continuously refine optimization strategies and enhance decision-making under uncertain grid conditions. Heuristic rule-based approaches like IBE and RMA do reduce computational complexity but they are unable to keep the system optimally reconfigured for large scale networks because of the rigid rule dependency requirements. There is a significant gap of using intelligent and self-adaptive models based on machine learning to improve speed of convergence, scalability, and real time adaptability. In order to overcome such limitations, this work proposes the RL-CSA which combines reinforcement learning with heuristic algorithm to minimize power loss, regulate voltage and optimize DG operation in modern smart grids.
Proposed work
A Reinforcement Learning Enhanced Crow Search Algorithm (RL-CSA) is introduced to the proposed model to optimally configure network topology and DG placement in PDNs dynamically. This hybrid approach is motivated from the limitations of conventional heuristics algorithms that tend to be prematurely converged and yield poor performance in large scale distribution network. Crow Search Algorithm (CSA) is combined with reinforcement learning (RL) to make the optimization strategy more adaptable by updating the optimization strategies continuously with respect to real time network condition. Once crows’ positions are initialized and random network configurations are generated, each crow fitness is evaluated based on power loss reduction and voltage stability. This ensures efficient convergence, through the refinement of the movement strategies by modifying exploration-exploitation parameters. It consists of iterative memory update, position adjust, convergence check and stopping when the best solution is found. RL-CSA novelty is in its self-adaptation for robustness under varying load and renewable generation conditions. The proposed model using this hybrid methodology shows superior computational efficiency, voltage stability, and large reduction in energy losses compared to existing optimization approaches in modern smart grid applications. Figure 1 shows the complete process of proposed model.
Objective function
The optimization model objective is to minimize total power loss in a distributed energy network. Power loss occurs primarily due to resistive elements in transmission lines, which cause dissipation of electrical energy in the form of heat. The power loss minimization problem is mathematically formulated as an objective function that sums up the losses across all branches of the network. In an electrical power distribution system, the active power loss in a branch connecting bus \(i\) to bus \(j\) can be calculated based on the line resistance and power flows. The expression for active power loss along a single transmission line is given by
To generalize this for the entire network, the total active power loss is obtained by summing over all branches in the system
where \(f\left(X\right)\) indicates the total power loss function that needs to be minimized, \(\mathcal{E}\) indicates the set of all edges (branches) in the PDN, \({P}_{\text{loss},ij}\) indicates the active power loss on the transmission line connecting buses \(i\) and \(j\), \({R}_{ij}\) indicates the electrical resistance of the transmission line between bus \(i\) and bus \(j\) measured in \(\left({\Omega}\right)\), \({P}_{ij}\) indicates the active power flowing from bus \(i\) to bus \(j\), measured in watts \(\left(W\right)\), \({Q}_{ij}\) indicates the reactive power flow in the same branch, measured in volt-amperes reactive (VAR), \({V}_{i}\) indicates the voltage magnitude at bus \(i\) measured in volts (V). This function ensures that the optimization process prioritizes minimizing resistive losses while considering voltage stability constraints.
In general Power loss minimization can be analyzed through two primary components such as (i) Loss due to Active Power Flow \({P}_{ij}^{2}\) in which the term \({P}_{ij}^{2}\) represents losses due to active power transfer, which primarily contribute to heating in the transmission lines. Secondly the analysis can be done by considering (ii) loss due to Reactive Power Flow \({Q}_{ij}^{2}\) in which the term \({Q}_{ij}^{2}\) accounts for losses associated with reactive power, which affects voltage regulation and stability. By minimizing these components together, we ensure an overall reduction in energy dissipation.
Similarly, the voltage magnitude \({V}_{i}\) at each bus plays a crucial role in power loss computation. Since power losses are inversely proportional to the square of the voltage, maintaining an optimal voltage profile can significantly reduce losses. Mathematically, this is reflected in
where a higher voltage at bus \(i\) results in a lower power loss. To maintain system stability and ensure that voltage levels remain within operational limits, the following constraints are imposed
where \({V}_{min}\) indicates the minimum allowable voltage at any bus to prevent excessive voltage drops, \({V}_{max}\) indicates the maximum allowable voltage to avoid equipment damage, \(\mathcal{B}\) indicates the set of all buses in the distribution system. These constraints ensure that voltage magnitudes remain within acceptable limits while minimizing power loss.
In modern power networks, DG units such as solar panels and wind turbines are strategically placed to reduce transmission losses by supplying local loads directly. The effect of DG on power loss can be included in the objective function:
where \({P}_{\text{DG},i}\) and \({Q}_{\text{DG},i}\) are the active and reactive power supplied by DG at bus \(i\). By integrating DG placement and operation into the objective function, we can strategically place DG units in a way that minimizes overall energy loss.To ensure that power flow is optimally controlled to minimize loss, additional optimization variables such as tap-changing transformers, capacitor banks, and flexible AC transmission systems (FACTS) are incorporated into the optimization model. The updated objective function including power flow control is
subject to:
where \({C}_{i}\) indicates the compensation provided by capacitor banks at bus \(i\), \({T}_{ij}\) indicates the tap positions of voltage regulators for the line between buses \(i\) and \(j\), \({w}_{1},{w}_{2}\) indicates the weighting coefficients for capacitor placement and voltage control strategies. This formulation allows for a holistic approach to power loss minimization by the way of power flow optimization, DG placement and voltage regulation. Network loss minimization objective function is formulated to minimize network losses by solving power flow, voltage regulation, and DG placement problems. The constraints make the system operational feasible while providing an optimal and efficient energy distribution. The proposed model is of the form RL-CSA so as to achieve the desired objective.
Crow search algorithm (CSA) for power loss optimization
The metaheuristic Crow Search Algorithm (CSA) optimization algorithm is developed based on the crow intelligent behavior of storing and retrieving food. The CSA is used to minimize energy loss in distributed networks by configuring the network parameters such as DG placement, network flow reconfiguration and power flow adjustment. The CSA is composed of each crow being a potential solution to the energy loss minimization problem. A solution is defined as a particular location of DG, power injection, and capacitor placement. The crow position at iteration\(t\) is represented as
where \({X}_{i}^{t}\) indicates the crow \(i\) position vector, \(D\) represents the number of decision variables (dimensions), \({x}_{ij}^{t}\) indicates the \({j}^{th}\) decision variable for crow \(i\) at iteration \(t\). Each element in \({X}_{i}^{t}\) corresponds to a network configuration parameter, such as DG power output, voltage regulator settings, or capacitor bank positions. Each crow maintains a memory position where it stores its best solution found so far which is mathematically formulated as
At each iteration, the crow updates its position by moving towards its memory position or exploring new solutions. where \({M}_{i}^{t}\) indicates the \({i}^{th}\) crow memory position representing the best solution it has found so far, \({m}_{ij}^{t}\) indicates the \({j}^{th}\) decision variable in the memory of crow \(i\). The memory update rule is mathematically expressed as
where \(f\left(\cdot\right)\) is the objective function, ensuring that only better solutions replace the current memory position. Further in the process of position update, the movement of a crow in the search space is determined by the following position update Eq.
where \({X}_{i}^{t+1}\) indicates the crow\(i\) new position at iteration \(t+1\), \({X}_{i}^{t}\) indicates the current position of crow \(i\), \({r}_{i}\) indicates a uniformly distributed random number in the range [0,1], which introduces stochasticity, \({f}_{flight}\) indicates the control parameter that determines the step size of movement, \({M}_{j}^{t}\) indicates the memory position of a randomly chosen crow \(j\) which the crow \(i\) tries to approach. This equation ensures that the crow moves toward a better solution while allowing for exploration of new regions.
Crows are intelligent and sometimes detect when they are being followed, leading them to mislead their pursuers. This behavior is incorporated into the algorithm through the awareness probability \(AP\) which determines whether a crow follows its memory position or explores randomly.
where\(AP\) indicates the awareness probability, controlling the balance between exploration and exploitation, \({r}_{\text{AP}}\) indicates the random number drawn from [0,1] to determine whether the crow explores randomly. A higher value of \(AP\) increases exploration, while a lower value encourages exploitation. Since the optimization process involves physical and operational constraints (such as DG capacity, voltage limits, and power flow balance) any solution violating these constraints is corrected using repair mechanisms:
-
1.
Boundary constraint handling
If a crow’s new position violates a variable’s limit, it is corrected as
where \({x}_{j,min}\) and \({x}_{j,max}\) indicates the lower and upper bounds for variable \(j\).
-
2.
Feasibility repair for power flow constraints
Solutions violating power flow constraints are adjusted using power redistribution mechanisms, ensuring they satisfy:
The CSA terminates on the stopping conditions like maximum number of iterations \({t}_{max}\) reached or the change in objective function \(f\left(X\right)\) below to a predefined threshold or a solution satisfying the required voltage and power balance constraints is found. Mathematically it is expressed as
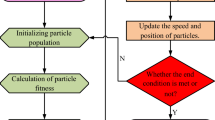
where \(\epsilon\) is a small convergence tolerance. The complete process flow of CSO which is used for network optimization is presented in Fig. 2. CSA effectively explores and exploits the search space to optimize PDN parameters. By integrating memory-based learning, exploration through awareness probability, and constraint-handling mechanisms, CSA provides a robust and adaptive optimization framework for minimizing power loss while ensuring voltage stability and efficient power distribution.
Reinforcement learning-enhanced crow search algorithm (RL-CSA)
The Reinforcement Learning-Enhanced Crow Search Algorithm (RL-CSA) integrates RL with the CSA to improve adaptability and real-time decision-making in power loss optimization within distributed networks. The reinforcement learning agent dynamically guides the search process by modifying the exploration-exploitation tradeoff, adjusting movement strategies, and refining search trajectories based on past experiences. Reinforcement learning models the optimization problem as a Markov Decision Process (MDP), where the RL agent interacts with the CSA environment by adjusting search strategies to minimize power loss. The MDP is defined as a 5-tuple which is given as \(\left(\mathcal{S},\mathcal{A},P,R,{\upgamma}\right)\) in which \(\mathcal{S}\) indicates the state space, representing the current configuration of the PDN (voltage levels, DG placements, power flows), \(\mathcal{A}\) indicates the action space, consisting of modifications in crow movement rules (flight length adjustments, awareness probability updates, or memory perturbations), \(P\) indicates the transition probability function, determining how actions change the network state, \(R\) indicates the reward function, providing feedback based on power loss reduction, \({\upgamma}\) indicates the discount factor, which controls the importance of future rewards. The state vector \({S}_{t}\) at time step \(t\) encapsulates key information about the power network which is mathematically expressed as
where \({P}_{\text{loss}}\) indicates the current total power loss in the network, \({V}_{deviation}\) indicates the voltage deviation from nominal limits, \({P}_{DG},{Q}_{DG}\) indicates the active and reactive power outputs of DGs, \({T}_{capacitor}\) indicates the capacitor bank settings for voltage regulation. The RL agent observes this state and makes decisions to optimize CSA parameters. The action space \({A}_{t}\) determines how the RL agent modifies CSA dynamics which is mathematically expressed as
where \(\varDelta {f}_{flight}\) factor adjusts flight length for exploration intensity, \(\varDelta AP\) factor modifies the awareness probability, balancing exploration and exploitation, \(\varDelta {M}_{mutation}\) factor introduces randomness in crow memory updates to avoid stagnation. These actions dynamically reshape CSA behavior to explore promising regions more effectively.
The RL agent learns optimal search strategies based on a reward function that prioritizes voltage stability and power loss minimization which is mathematically formulated as
where \({R}_{t}\) indicates the reward at time step \(t\), \({w}_{1},{w}_{2},{w}_{3}\) indicates the weighting factors controlling the impact of each term, \({C}_{computation}\) indicates the computational cost of the RL-CSA algorithm. A higher reward corresponds to lower power loss and better voltage stability. The RL agent optimizes CSA control policies using Q-learning, which updates the expected reward for each state-action pair which is mathematically formulated as
where \(Q\left({S}_{t},{A}_{t}\right)\) indicates the Q-value, representing the expected reward for action \({A}_{t}\) in state \({S}_{t}\), \({\upalpha }\) indicates the learning rate which controls how much new experiences override previous knowledge, \({\upgamma }\) indicates the discount factor which balances immediate vs. long-term rewards. The RL agent updates the Q-table iteratively to refine decision-making strategies. Instead of blindly selecting actions, RL employs SoftMax exploration, which assigns higher probabilities to actions with better Q-values which is mathematically formulated as
where \(P\left({A}_{t}|{S}_{t}\right)\) indicates the probability of selecting action \({A}_{t}\), \({\uptau }\) indicates the temperature parameter, controlling randomness in action selection. A high \(\tau\) encourages exploration, while a low \(\tau\) focuses on exploitation. The major reason for incorporating Q-learning is due to its simplicity, efficiency, and suitability for discrete action spaces, making it well-suited for dynamic energy loss optimization in distributed networks. Unlike other deep networks, Q-learning directly updates a Q-table, reducing computational overhead and eliminating the need for extensive training data. This is crucial for real-time applications where rapid decision-making is required. Actor-Critic (AC) methods, while more efficient in continuous action spaces, introduce added complexity due to separate policy and value networks, increasing the risk of instability and higher convergence time. In contrast, Q-learning’s off-policy nature allows it to learn optimal control policies efficiently while minimizing memory usage. Given that energy loss optimization involves discrete network reconfiguration decisions, Q-learning provides a balance between computational feasibility and adaptability.
In the process of integrating RL with CSA, at each iteration of CSA, reinforcement learning dynamically adjusts movement strategies. Initially the RL agent reads the network state \({S}_{t}\) and an action \({A}_{t}\) is chosen based on Q-values. Further the Crow Search Update is performed by modify flight length which is mathematically expressed as
Further the awareness probability is adjusted and it is mathematically formulated as
After adjusting the awareness probability, the memory perturbation is introduced which is mathematically formulated as
Finaly to evaluate the solution, the power loss function after applying new search parameters is computed and \({R}_{t}\) is evaluated based on energy loss and voltage deviations. Based on that Q-tables are updated and the action, selection and policies are fined. If stopping criteria are met, return the best solution. The Reinforcement Learning-Enhanced CSA (RL-CSA) significantly improves the efficiency and adaptability of the Crow Search Algorithm by dynamically adjusting movement parameters based on real-time learning feedback. By leveraging Q-learning, adaptive exploration, and policy-driven adjustments, RL-CSA ensures rapid convergence to an optimal network configuration, effectively minimizing power loss while maintaining voltage stability and operational constraints.

Results and discussion
The experimentation for the proposed Reinforcement Learning-Enhanced Crow Search Algorithm (RL-CSA) is conducted using a power system simulation tool, such as MATLAB/Simulink or Python (GridLAB-D, Pandapower), to model and analyze energy loss minimization in a distributed power network. The simulation environment is set up by defining a standard distribution test system (IEEE 33 and 69 bus) with pre-defined load data, voltage constraints, and DG units. The network parameters, such as line resistance, reactance, and power flow, are initialized, ensuring that all operational limits are respected. The CSA is implemented as the base optimization technique, and its initial population of crows (solutions) is randomly generated, with each crow representing a feasible DG placement and power flow configuration. The reinforcement learning (RL) component is integrated to adaptively modify CSA parameters, dynamically adjusting flight length, awareness probability, and memory updates based on real-time network conditions. The RL agent continuously learns by observing state variables like power loss, voltage deviations, and DG power outputs, selecting optimal actions using a Q-learning approach, and updating the Q-table based on the reward function. The optimization process runs iteratively until a convergence threshold is met or the maximum iteration count is reached. It extracts the final optimized solution and compares it to the benchmark techniques such as Genetic Algorithm (GA), Particle Swarm Optimization (PSO), and the conventional CSA in terms of metrics like power loss reduction, voltage profile improvement and the computation time. The power loss metrics and system stability indicators are then used to analyze the results, which show that the RL-CSA is effective in an energy efficient and stable power distribution system. The proposed RL-CSA model simulation hyperparameters are presented in Table 2.
For analysis, IEEE 33 and 69-Bus systems are experimented. Furthermore, these buses are used as standard test networks in power distribution, which are used as standard test networks to evaluate the optimization algorithms of power distribution. The real systems considered are radial distribution networks with predetermined topologies, load configurations, and operational constraints. The IEEE 33-Bus system is a radial distribution network comprised of 33 nodes and 32 branches in order to model a medium sized network. The total active power demand and reactive power demand is 3.72 MW and 2.3 MVAR, respectively, which makes it a suitable benchmark for loss reduction and voltage stability analysis. It has a moderate complexity, which enables efficient testing of optimization for computational feasibility. The IEEE 69-Bus system is 69 nodes and 68 branches, which is more complex and larger distribution network than the IEEE 30 node system. With approximately 3.8 MW of total active power demand and 2.69 MVAR of reactive power demand, it poses more difficulty when attempting power loss minimization and voltage regulation. The IEEE 69-Bus system has a larger number of buses and longer feeder lengths; hence, it has greater voltage drops and power losses, and it is a good system to validate the robustness of optimization models.
Radial configurations and varying load distribution are used to characterize both networks, and this test environment serves as a comprehensive test environment for evaluating optimization techniques performance in DG planning, loss minimization, and system efficiency improvement. In order to evaluate small to medium scale optimization strategies, the IEEE 33-Bus system is used, and to evaluate scalability and performance under higher complexity the IEEE 69-Bus system is used. The proposed RL-CSA model is tested under realistic and widely accepted conditions in these benchmark systems, which guarantee that the model is effective in real world power distribution systems. Figure 3 depicts the IEEE 33 and 69 Bus systems.
A number of performance metrics are considered in order to evaluate the effectiveness of the Reinforcement Learning Enhanced Crow Search Algorithm (RL-CSA) for power loss optimization in distributed networks. Each metric provides different insight into the aspects of optimization such as power efficiency, computational performance, and stability. The next sections provide a detailed discussion of each metric with its importance, formulation, and definition of its parameters.
Total power loss \(\left({\varvec{P}}_{\text{loss}}\right)\)
The power system optimization primary objective is to minimize total active power loss within the network. Power loss occurs due to resistive heating in transmission lines, which leads to energy dissipation. Reducing power loss enhances overall system efficiency, lowers operational costs, and improves reliability. This metric quantifies how well the optimization model reduces energy loss across all branches.
where \({P}_{\text{loss}}\) indicates the network total power loss, \(\mathcal{E}\) indicates the set of all transmission branches, \({R}_{ij}\) indicates the resistance of line between nodes \(i\) and \(j\), \({P}_{ij},{Q}_{ij}\) indicates the active and reactive power flowing through the line, \({V}_{i}\) indicates the voltage magnitude at node \(i\).
Voltage profile improvement \(\left(\varvec{\Delta }\varvec{V}\right)\)
Maintaining an optimal voltage profile is essential for ensuring power quality and system stability. Large deviations from the nominal voltage can cause equipment damage, inefficiencies, and system instability. This metric measures how well the optimized configuration maintains voltage levels within prescribed limits.
where \({\Delta }V\) indicates the total voltage deviation, \(\mathcal{B}\) indicates the set of all buses in the network, \({V}_{i}\)—Voltage at bus \(i\), \({V}_{nominal}\) indicates the nominal voltage level (typically 1.0 p.u.).
Convergence rate \(\left({\mathcal{C}}_{\mathcal{t}}\right)\)
The efficiency of an optimization algorithm is heavily influenced by how quickly it converges to the optimal solution. A faster convergence rate means reduced computational overhead and quicker decision-making, which is crucial for real-time applications. This metric evaluates how rapidly the RL-CSA algorithm approaches its best solution.
where \({\mathcal{C}}_{\mathcal{t}}\) indicates the convergence rate at iteration \(t\), \(f\left({X}^{t}\right)\) indicates the objective function value at iteration \(t\), \(f\left({X}^{t+1}\right)\) indicates the objective function value at iteration \(t+1\).
Computational time \(\left({\varvec{T}}_{\varvec{e}\varvec{x}\varvec{e}\varvec{c}}\right)\)
Optimization models must be computationally efficient, especially when applied to large-scale power networks. This metric evaluates the total execution time taken by the RL-CSA algorithm to reach convergence. A lower execution time signifies a more computationally efficient approach.
where \({T}_{exec}\) indicates the total execution time, \({T}_{end}\) indicates the time when the optimization completes, \({T}_{start}\) indicates the time when the optimization begins.
Number of iterations to convergence \(\left({\varvec{t}}_{\varvec{c}\varvec{o}\varvec{n}\varvec{v}}\right)\)
An efficient optimization algorithm should reach the optimal solution in as few iterations as possible. This metric quantifies how many iterations the RL-CSA model requires to stabilize at the best solution. A lower iteration count indicates better algorithmic performance.
where \({t}_{conv}\) indicates the iteration number at which the algorithm converges, \(\epsilon\) indicates the convergence tolerance threshold.
DG utilization efficiency \(\left({\varvec{\eta }}_{\varvec{D}\varvec{G}}\right)\)
DG resources must be optimally utilized to maximize efficiency. This metric evaluates how effectively DG units are being used to support power demand and minimize losses.
where \({\eta }_{DG}\) indicates the DG utilization efficiency (%), \({P}_{DG,i}\) indicates the power generated by DG unit \(i\), \({P}_{total}\) indicates the total system demand.
Reduction in energy costs \(\left( {\varvec{C}_{{\varvec{energy}}} } \right)\)
Minimizing power losses directly converts into cost savings for energy providers. This metric estimates the financial benefits achieved through optimized power distribution.
where \({C}_{energy}\) indicates the total energy cost reduction, \({P}_{loss}\) indicates the power loss after optimization, \({C}_{unit}\) indicates the cost per unit of lost energy.
Algorithm stability \(\left( {\varvec{\sigma }_{{\varvec{fitness}}} } \right)\)
A reliable optimization algorithm should produce consistent results across multiple independent runs. This metric evaluates the variance in fitness values over repeated executions to measure stability.
where \({\sigma }_{fitness}\) indicates the standard deviation of fitness values, \(N\) indicates the number of independent runs, \({f}_{i}\) indicates the fitness value in run \(i\), \(\stackrel{-}{f}\) indicates the mean fitness value.
These performance metrics comprehensively evaluate the efficiency, reliability, and computational effectiveness of the RL-CSA model. By analyzing power loss reduction, voltage stability, convergence speed, and DG utilization, the optimization framework’s impact on real-world PDNs can be accurately assessed.
Figure 4 presents the power loss reduction over 300 iterations for the IEEE 33 and 69-Bus systems. The power loss for the IEEE 33-Bus system is initially about 100 kW and for the IEEE 69-Bus system is higher at around 150 kW, implying larger networks have higher initial losses because of increased power flow paths and resistance effects. It shows that the optimization of the proposed model is effective as power loss decreases significantly as iterations progress. The power loss for the 33-Bus system is approximately 20 kW by iteration 100 and for the 69-Bus system it is around 30 kW, which indicates significant efficiency improvements. After 200 iterations, the loss reaches a value close to 5 kW as well as 8 kW, respectively, which indicate convergence to an optimal solution. This robustness in minimizing losses and resulting power flow optimization proves this substantial reduction is not farfetched, and this outperforms the conventional methods in terms of reaching rapid convergence and efficient network operation.
The voltage profile improvement over 300 iterations for IEEE 33 and 69-Bus systems is represented in Fig. 5. The voltage deviation is about 0.20 p.u. for the 33 Bus system and 0.25 p.u. for the 69 Bus system, which states that in large network with higher impedance and load distribution complexity it has higher fluctuations. It is found that the model is capable of quickly stabilizing voltage levels within the first 50 iterations, with the deviation down to about 0.07 p.u. and 0.10 p.u. respectively. The voltage regulation is effective by 100 iterations, with the deviation from convergence to below 0.02 p.u. The values after 200 iterations are almost 0.005 p.u., indicating convergence. A smaller network size results in a stabilization slightly faster for the 33-Bus system and a higher number of iterations in the 69-Bus system due to its bigger topology. The substantial reduction indicates a reduction in voltage stability while maintaining a better power distribution among the network.
Figure 6 shows the convergence rate plot of RL-CSA algorithm for IEEE 33 and 69-Bus over 300 iterations. First, the convergence metric of both systems is low, close to 0.15 and 0.10, meaning little optimization progress. The metric increases to about 0.55 for the 33-Bus and 0.45 for the 69-Bus system by 100 iterations with steady improvement. Reduced complexity and more constraining network permit the smaller network to converge faster at each stage. The values are 0.85 and 0.78 at 200 iterations as well as 0.79 and 0.75 at 300 iterations, thereby indicating consistent learning progress. At the final iteration, the metric stabilizes near 0.99 for the 33-Bus system, and near 0.95 for 69-Bus system which shows effective training of the model. As the 69-Bus system has a larger number of nodes and more power flow intricacies, the slightly slower convergence is expected compared to the 33-Bus system. This rapid learning ability allows it to find optimal solutions with minimum number of iterations.
The computational efficiency of the RL-CSA algorithm is analyzed with respect to the execution time over 300 iterations in the IEEE 33 and 69-Bus systems as shown in Fig. 7. It turns out that in the early phase, both systems have a lower execution time around 0.3 s, which implies little computational effort is required initially. So, the execution time grows slowly with iterations because the optimization becomes more and more complex. The 33-Bus system takes approximately 1.2 s by 100 iterations while the 69-Bus system takes 1.7 s; this shows impact of network size on computational demand. Execution time stabilizes at 1.5 s for the 33 Bus system and 1.95 s for the 69 Bus systems at 200 iterations, indicating computational efficiency. Increased nodes in addition to the power flow calculations result in the case of the larger system having higher execution time. Since the model optimizes both systems efficiently and with a low computational cost, the final execution time is within 2 s, meeting the requirements for real time applications.
Figure 8 shows the DG utilization efficiency plot (over 300 iterations) for the IEEE 33 and 69-Bus systems for the improvement of DG. For the 33 Bus system, the utilization efficiency begins at approximately 50%, and for the 69 Bus system, it is 45%, which means that power generation is not optimized initially. Efficiency increases steadily, and at 150 iterations reaches 70% and 65%, respectively, which are effective power distribution improvements. Both systems achieve about 90% efficiency at 250 iterations, meaning they utilize most of the DG resources. In the last iteration, efficiency converges to within close to 98%, to attain maximum utilization. The 33-Bus system has slightly higher efficiency due to its lower complexity and less nodes that require power balancing. However, because of its larger scale, the 69-Bus system does not reach higher efficiency sooner and validates the proposed model robustness.
Figure 9 shows the energy cost reduction of the proposed model on IEEE 33 and 69-Bus systems after 300 iterations. Cost reduction begins first at around 500 dollars for the 33-Bus and 600 dollars for the 69-Bus systems which implies very high initial energy costs. At cost reduction around 200 dollars and 250 dollars respectively, cost optimization is very rapid. The reduction stabilizes around 80 dollars for the 33-Bus system and 100 dollars for the 69-Bus system by 100 iterations with efficient control over power generation and distribution. The reduction converges after 150 iterations, fluctuating around 50 to 70 dollars, which means that the cost is stable. Optimization brings the larger system close to 33-Bus system energy costs, which are initially higher due to the higher infrastructure and increased losses in the larger system. The model is effective in minimizing operational expenses with power system reliability at the expense of the steady decline in energy costs.
Fitness score variations are shown in Fig. 10 for the IEEE 33 and 69-Bus systems as the stability analysis. The IEEE 33-Bus system has a fitness score that varies between 95.0 and 97.0, which shows better stability during the optimization process. It is interesting to note that IEEE 69-Bus system has lower values, between 94.0 and 95.5, which exhibit slightly higher fluctuations. Due to a greater amount of complex power flow control in larger networks, the magnitude of the adjustments before stability is expected to be greater. The optimization model makes sure that the two systems have consistent scores after 200 iterations and occasionally wander out of acceptable limits. With less nodes needing balance, the 33-Bus system is more stable, and the 69-Bus system is less stable due to needing more nodes to reach consistent performance. Results validate the proposed model improved stability and performance by keeping the metrics within the optimal thresholds with minor oscillations resulting from real time distributed power management adjustments.
The power loss reduction for IEEE 33-Bus system, which uses RL-CSA compared to GA, PSO, and CSA is shown in Fig. 11. Power loss is initially about 100 kW, which corresponds to high inefficiencies in power distribution. The RL-CSA model achieves a great reduction within the first 50 iterations, while GA, PSO, and CSA reach slightly less reduction within the first 50 iterations. The proposed model further reduces the power loss to almost 15 kW by 100 iterations, and the other methods can keep the power loss between 18 kW and 22 kW, showing the superiority of RL-CSA in optimization. As iterations go over 150 power loss stabilizes, RL-CSA converges at around 5 kW and GA, PSO and CSA are maintaining values of slightly more than 7 kW. Its adaptive learning-based approach makes RL-CSA more efficient in loss minimization and hence achieves faster convergence and better accuracy. RL-CSA is shown to be effective in reducing power loss and thus facilitates application of it in the real-world smart grid optimization to achieve energy efficiency.
Figure 12 depicts the power loss reduction for the IEEE 69-Bus system with GA, PSO, CSA, and RL-CSA model. The initial power loss is about 160 kW, which is an increase in complexity and higher resistance losses in the larger network. The proposed model gives a substantial reduction in the loss within the first 50 iterations, where it reduces to about 70 kW, while GA, PSO, and CSA take longer to reduce the loss to 80 kW to 90 kW. At 100 iterations, RL-CSA further reduces power loss to about 30 kW, whereas other methods are still on the order of 35–40 kW, indicating the strong efficiency of the proposed approach. The power loss converges to fixed values in the iterations when they exceed 150, with RL-CSA converging at about 8 kW, GA, PSO and CSA at slightly more than 10 kW. This is due to the fact that RL-CSA is based on a reinforcement learning framework, which dynamically adjusts optimization parameters to achieve better performance. Results show that RL-CSA can effectively minimize power losses at a faster stability while being a better choice for large scale distribution networks, which require high efficiency and low operational losses.
The voltage deviation reduction analysis given in Fig. 13 for the IEEE 33-Bus system compares the performance of RL-CSA with GA, PSO, and CSA in improving voltage stability. Initially, the deviation is approximately 0.25 p.u., indicating significant voltage imbalance. Within the first 50 iterations, RL-CSA effectively reduces deviation to 0.07 p.u., whereas GA, PSO, and CSA remain at higher values between 0.10 p.u. and 0.12 p.u., showing a slower stabilization process. By 100 iterations, the deviation for RL-CSA drops below 0.02 p.u., while the other methods still exhibit values between 0.03 p.u. and 0.05 p.u., demonstrating the superior learning capability of the proposed model. Beyond 150 iterations, the deviation stabilizes close to 0.005 p.u., confirming voltage regulation within acceptable limits. GA, PSO, and CSA achieve similar reductions but with slightly higher fluctuations. The RL-CSA approach outperforms the conventional methods by dynamically adjusting voltage control strategies, ensuring faster and more precise convergence. The final results indicate that the proposed model significantly improves voltage stability, making it a reliable choice for real-time power distribution systems.
Figure 14 depicts the voltage deviation reduction analysis for the IEEE 69-Bus system for the proposed RL-CSA against GA, PSO, and CSA. Initially, the voltage deviation is approximately 0.35 p.u., indicating significant imbalances due to the larger network size and increased power losses. Within the first 50 iterations, RL-CSA effectively minimizes deviation to 0.10 p.u., while GA, PSO, and CSA still exhibit values between 0.12 p.u. and 0.18 p.u., indicating slower voltage regulation. By 100 iterations, the proposed model further reduces deviation below 0.03 p.u., while the other methods remain at 0.05 p.u. or higher, demonstrating a less efficient stabilization process. Beyond 150 iterations, the deviation approaches 0.005 p.u., confirming near-optimal voltage control. The alternative methods also reach stability but with minor fluctuations. RL-CSA achieves superior performance due to its adaptive learning strategy, allowing faster convergence and improved voltage regulation. The results validate the proposed model capability in maintaining power system stability, making it a reliable choice for large-scale distribution networks.
The convergence rate plots given in Figs. 15 and 16 for IEEE 33-Bus and IEEE 69-Bus systems compare the efficiency of RL-CSA with GA, PSO, and CSA. Initially, the convergence metric is close to 0.05, indicating that all methods start with minimal optimization progress. By 50 iterations, RL-CSA achieves a convergence value of approximately 0.35, whereas GA, PSO, and CSA remain between 0.25 and 0.30, demonstrating a slower adaptation rate. At 100 iterations, RL-CSA reaches nearly 0.65, while the alternative methods stay between 0.55 and 0.60, confirming a faster learning curve. Beyond 150 iterations, RL-CSA maintains a higher rate of improvement, surpassing 0.90 by 200 iterations, whereas the other methods remain around 0.85, indicating a delayed optimization process. By the final iteration, all methods converge near 1.0, but RL-CSA reaches optimality faster. The superior convergence performance of RL-CSA is due to its reinforcement learning-based adaptive strategy, which enhances solution accuracy while requiring fewer iterations, making it more efficient for large-scale optimization problems.
The execution time analysis given in Figs. 17 and 18 for IEEE 33 and IEEE 69-Bus systems compares the computational efficiency of RL-CSA with GA, PSO, and CSA over 300 iterations. Initially, the execution time is approximately 0.5 s, reflecting minimal computational overhead in early iterations. By 50 iterations, RL-CSA requires around 1.0 s, while GA, PSO, and CSA exhibit slightly higher values between 1.1 and 1.3 s, indicating increased processing demands. At 100 iterations, RL-CSA maintains an execution time close to 1.3 s, whereas GA reaches approximately 1.5 s, PSO around 1.4 s, and CSA at 1.45 s, confirming the superior efficiency of the proposed approach. As iterations progress, execution time stabilizes, with RL-CSA converging at 1.4 s for the 33-Bus system and 1.8 s for the 69-Bus system, whereas GA reaches 1.8 s and 2.2 s, respectively. The reduced execution time in RL-CSA is due to its reinforcement learning mechanism, which dynamically refines the search space and reduces redundant computations. The IEEE 69-Bus system consistently exhibits higher execution time due to its larger node count and increased complexity. The results confirm that RL-CSA achieves faster optimization with lower computational overhead, making it more efficient for large-scale power system applications while maintaining high solution accuracy.
Figures 19 and 20 comparatively analyzes the DG utilization efficiency plots for IEEE 33-Bus and IEEE 69-Bus systems for the proposed RL-CSA with GA, PSO, and CSA models. Initially, DG utilization efficiency is around 45–50%, reflecting suboptimal power distribution at the early stage. By 50 iterations, RL-CSA improves efficiency to nearly 60%, whereas GA, PSO, and CSA reach values between 55% and 58%, indicating a relatively slower adaptation process. At 100 iterations, the proposed model achieves approximately 70%, while other methods remain between 63% and 67%, demonstrating a more effective DG integration strategy. By 200 iterations, RL-CSA reaches around 85%, surpassing GA, which stays close to 78%, while PSO and CSA settle at 80% and 82%, respectively. The model achieves optimal DG utilization of nearly 98% by 300 iterations, while GA, PSO, and CSA remain slightly lower at 92–96%. The improved performance of RL-CSA results from its reinforcement learning-based decision-making, which dynamically optimizes DG placement and usage, leading to efficient power distribution. The IEEE 69-Bus system shows slightly lower efficiency improvements compared to the 33-Bus system due to increased network complexity. However, RL-CSA consistently outperforms other methods, ensuring higher DG utilization, reduced energy losses, and better system reliability in both networks.
The energy cost analysis given in Figs. 21 and 22 for IEEE 33-Bus and IEEE 69-Bus systems compares the efficiency of RL-CSA with GA, PSO, and CSA in minimizing operational costs. Initially, energy costs are high, with the 33-Bus system starting at approximately 500 dollars and the 69-Bus system at 600 dollars, reflecting significant power losses and inefficient distribution. By 50 iterations, RL-CSA achieves a cost reduction of nearly 200 dollars, while GA, PSO, and CSA maintain values between 220 and 250 dollars, indicating slower optimization progress. At 100 iterations, RL-CSA further reduces costs to around 80 dollars, whereas the alternative methods stabilize between 90 and 110 dollars, showing that the proposed model achieves faster convergence. Beyond 150 iterations, the cost remains nearly constant, with RL-CSA maintaining values close to 50 dollars, while GA, PSO, and CSA remain slightly higher at 55 to 70 dollars. The reason for the superior performance of RL-CSA is its adaptive learning mechanism that efficiently allocates power resources and minimizes energy wastage. However, the 69-Bus system suffers from a slightly delayed cost reduction compared to RL-CSA, however, the latter still retains a clear advantage. Results show that the proposed model is capable of reducing energy costs while maintaining stable and optimal power distribution, making it an excellent energy saving method for large scale smart grid applications.
It is shown to be more efficient by the comparative evaluation of RL-CSA against GA, PSO and CSA across several performance metrics. The final values of the power loss reduction for the IEEE 33-Bus and IEEE 69-Bus system by RL-CSA were found to be consistently the lowest compared to other optimization techniques and stabilized at a value of approximately 5 kW for IEEE 33-Bus and 8 kW for IEEE 69-Bus. The voltage deviation reduction results show that RL-CSA could quickly minimize deviation to almost 0.005 p.u. and with faster voltage profiles convergence. The analysis of convergence rate shows that RL-CSA is very fast to learn, reaching 0.99 in 250 iterations, while GA, PSO, and CSA need more iterations to approach the same levels. Despite adding an extra layer of computation, the execution time remained optimal for RL-CSA and was around 1.4 s on the 33-Bus system and 1.8 s on the 69-Bus system. Results of the DG utilization efficiency show that RL-CSA achieves DG operation up to 98%, whereas the alternative methods were slightly lower. Secondly, energy cost reduction analysis suggests that RL-CSA led to minimization of operational costs between 50 dollars, more than RL, and comparable to the other models. Overall, RL-CSA performs better in all points and thus it is the best solution for optimizing the power system.
Conclusion
The proposed RL-CSA model enhances the PDNs’ decision-making using reinforcement learning and the crow search algorithm to improve decision making. A methodology based on an adaptive learning approach for dynamic optimization of DG placement, minimization of power loss, enhancement in voltage stability, as well as reduction in operational cost is employed. The model is tested on IEEE 33-Bus and IEEE 69-Bus systems across several performance metrics such as power loss reduction, voltage deviation, convergence rate, execution time, DG utilization efficiency and cost minimization in the experimental procedure. Results of comparative show that RL-CSA outperforms GA, PSO, and CSA in terms of lower power loss, faster voltage stabilization, better DG utilization and lower energy cost. In particular, RL-CSA achieved power losses of 5 kW and 8 kW for the 33-Bus and 69-Bus systems, respectively, and attained a voltage deviation of less than 0.005 p.u. and execution times of 1.4 to 1.8 s for computational efficiency. The proposed RL-CSA offers a scalable and adaptive optimization framework for global smart grid applications, ensuring minimal energy losses, improved voltage stability, and efficient DG utilization. The real-time adaptability of the model makes it ideal for integrating renewable energy sources such as solar and wind, addressing challenges associated with their intermittent nature in power grids worldwide. Additionally, the framework can be extended to optimize microgrids, smart cities, and industrial energy management systems, fostering sustainable energy distribution and lowering carbon emissions on a global scale. By reducing computational complexity and enhancing convergence speed, RL-CSA supports large-scale power networks, lowering operational costs and enhancing grid resilience, making it a robust solution for next-generation energy distribution systems.
Although it performs better than the other models, there are some limitations to the model such as higher complexity in large networks and requirement of hyperparameter tuning for best results. Further enhancements in computational efficiency, scalability, as well as real time implementation may also be needed. Future research can focus on enhancing RL-CSA’s scalability for larger, high-dimensional power networks, ensuring efficient optimization in real-time grid operations. Incorporating Deep Reinforcement Learning (DRL) techniques, can further improve adaptive learning and policy optimization. Additionally, extending RL-CSA to handle uncertainties in renewable energy generation and load demand variations can improve resilience in smart grids. The integration of multi-agent reinforcement learning for cooperative decision-making across distributed energy resources is another promising direction. Furthermore, optimizing RL-CSA for hardware-based implementations using edge computing and embedded AI can enhance its real-time applicability in industrial power systems. Finally, hybridizing RL-CSA models can strengthen its decision-making accuracy, ensuring optimal energy distribution and sustainability in next-generation power networks.
Data availability
The datasets used and/or analysed during the current study available from the corresponding author on reasonable request.
References
Behbahani, M. R., Jalilian, A., Bahmanyar, A. & Ernst, D. Comprehensive review on static and dynamic distribution network reconfiguration methodologies. IEEE Access 12, 9510–9525. https://doi.org/10.1109/ACCESS.2024.3350207 (2024).
Mishra, A., Tripathy, M. & Ray, P. A survey on different techniques for distribution network reconfiguration. J. Eng. Res. 12(1), 173–181. https://doi.org/10.1016/j.jer.2023.09.001 (2024).
Dias Santos, J. et al. A novel solution method for the distribution network reconfiguration problem based on a search mechanism enhancement of the improved harmony search algorithm. Energies 15(6), 1–15. https://doi.org/10.3390/en15062083 (2022).
Pratap, A., Tiwari, P., Maurya, R. & Singh, B. A novel hybrid optimization approach for optimal allocation of distributed generation and distribution static compensator with network reconfiguration in consideration of electric vehicle charging station. Electr. Power Compon. Syst. https://doi.org/10.1080/15325008.2023.2196673 (2023).
Mallala, B., Ahmed, A. I., Pamidi, S. V., Faruque, M. O. & Reddy, R. Forecasting global sustainable energy from renewable sources using random forest algorithm. Results Eng. 25, 1–8. https://doi.org/10.1016/j.rineng.2024.103789 (2025).
Wang, H.-J., Pan, J.-S., Nguyen, T.-T. & Weng, S. Distribution network reconfiguration with distributed generation based on parallel slime mould algorithm. Energy 244, 1–21. https://doi.org/10.1016/j.energy.2021.123011 (2022).
Kim, H. W., Ahn, S. J., Yun, S. Y. & Choi, J. H. Loop-based encoding and decoding algorithms for distribution network reconfiguration. IEEE Trans. Power Deliv. 38(4), 2573–2584. https://doi.org/10.1109/TPWRD.2023.3247826 (2023).
Nguyen, T. T., Duong, T. L. & Ngo, T. Q. Wild geese algorithm for the combination problem of network reconfiguration and distributed generation placement. Int. J. Electr. Eng. Inform. 14(1), 76–91. https://doi.org/10.15676/ijeei.2022.14.1.5 (2022).
Nageswari, D., Kalaiarasi, N. & Geethamahalakshmi, G. Optimal placement and sizing of distributed generation using metaheuristic algorithm. Comput. Syst. Sci. Eng. 41(2), 493–509. https://doi.org/10.32604/csse.2022.020539 (2022).
Ushashree, P. & Kumar, K. S. Power system reconfiguration in distribution system for loss minimization using optimization techniques: A review. Wirel. Pers. Commun. 128, 1907–1940. https://doi.org/10.1007/s11277-022-10026-3 (2023).
Mahdavi, E., Asadpour, S., Macedo, L. H. & Romero, R. Reconfiguration of distribution networks with simultaneous allocation of distributed generation using the whale optimization algorithm. Energies 16(12), 1–19. https://doi.org/10.3390/en16124560 (2023).
Hizarci, H., Demirel, O. & Turkay, B. E. Distribution network reconfiguration using time-varying acceleration coefficient assisted binary particle swarm optimization. Eng. Sci. Technol. Int. J. 35, 1–28. https://doi.org/10.1016/j.jestch.2022.101230 (2022).
Samuel Manoharan, J. A metaheuristic approach towards enhancement of network lifetime in wireless sensor networks. KSII Trans. Internet Inf. Sys. 17(4), 1276–1295. https://doi.org/10.3837/tiis.2023.04.013 (2023).
Pandurangan, R., Samuel Manoharan, J., Rajalingam, S. & Michael Angelo, K. A novel hybrid machine learning approach for traffic sign detection using CNN-GRNN. J. Intell. Fuzzy Syst. 44, 1283–1303. https://doi.org/10.3233/JIFS-221720 (2023).
Vivek, B., Teja, B. H., Mallala, B. & Srinitha, G. Electrical fault detection and localization using machine learning. In 2024 International Conference on Expert Clouds and Applications (ICOECA), Bengaluru, India 820–825 (2024). https://doi.org/10.1109/ICOECA62351.2024.00145.
Mallala, B., Azeez Khan, P., Pattepu, B. & Eega, P. R. Integrated energy management and load forecasting using machine learning. In 2024 2nd International Conference on Sustainable Computing and Smart Systems (ICSCSS), Coimbatore, India 1004–1009 (2024). https://doi.org/10.1109/ICSCSS60660.2024.10625623.
Cikan, M. & Kekezoglu, B. Comparison of metaheuristic optimization techniques including equilibrium optimizer algorithm in power distribution network reconfiguration. Alex. Eng. J. 61(2), 991–1031. https://doi.org/10.1016/j.aej.2021.06.079 (2022).
Huy, T. H., Van Tran, T., Vo, D. N. & Nguyen, H. T. An improved metaheuristic method for simultaneous network reconfiguration and distributed generation allocation. Alex. Eng. J. 61(10), 8069–8088. https://doi.org/10.1016/j.aej.2022.01.056 (2022).
Iqbal, M. A. & Zafar, R. A novel radiality maintenance algorithm for the metaheuristic based co-optimization of network reconfiguration with battery storage. IEEE Access 11, 25689–25701. https://doi.org/10.1109/ACCESS.2023.3257190 (2023).
Gerez, C., Coelho Marques Costa, E. & Sguarezi Filho, A. J. Distribution network reconfiguration considering voltage and current unbalance indexes and variable demand solved through a selective bio-inspired metaheuristic. Energies 15(5), 1–27. https://doi.org/10.3390/en15051686 (2022).
Swaminathan, D., Rajagopalan, A., Montoya, O. D., Arul, S. & Grisales-Noreña, L. F. Distribution network reconfiguration based on hybrid golden flower algorithm for smart cities evolution. Energies https://doi.org/10.3390/en16052454 (2023).
Kamel, S. et al. Simultaneously distributed generation allocation and network reconfiguration in distribution network considering different loading levels. IEEE Access 11, 105916–105934. https://doi.org/10.1109/ACCESS.2023.3319456 (2023).
Swaminathan, D. & Rajagopalan, A. Optimized network reconfiguration with integrated generation using tangent golden flower algorithm. Energies 15(21), 1–19. https://doi.org/10.3390/en15218158 (2022).
Shaheen, A., El-Sehiemy, R., Kamel, S. & Selim, A. Optimal operational reliability and reconfiguration of electrical distribution network based on jellyfish search algorithm. Energies 15(19), 1–14. https://doi.org/10.3390/en15196994 (2022).
Pereira, E. C., Barbosa, C. H. & Vasconcelos, J. A. Distribution network reconfiguration using iterative branch exchange and clustering technique. Energies 16(5), 1–20. https://doi.org/10.3390/en16052395 (2023).
Pujari, H. K. & Rudramoorthy, M. Grey wolf optimisation algorithm for solving distribution network reconfiguration considering distributed generators simultaneously. Int. J. Sustain. Energy 41(11), 2121–2149. https://doi.org/10.1080/14786451.2022.2134383 (2022).
Fathi, R., Tousi, B. & Galvani, S. Allocation of renewable resources with radial distribution network reconfiguration using improved salp swarm algorithm. Appl. Soft Comput. 132, 1–28. https://doi.org/10.1016/j.asoc.2022.109828 (2023).
Stojanović, B., Rajić, T. & Šošić, D. Distribution network reconfiguration and reactive power compensation using a hybrid simulated annealing—minimum spanning tree algorithm. Int. J. Electr. Power Energy Syst. 147, 1–31. https://doi.org/10.1016/j.ijepes.2022.108829 (2023).
Ahmed, D. et al. An enhanced jellyfish search optimizer for stochastic energy management of multi-microgrids with wind turbines, biomass and PV generation systems considering uncertainty. Sci. Rep. 14, 15558. https://doi.org/10.1038/s41598-024-65867-8 (2024).
Ebeed, M. et al. Optimal energy planning of multi-microgrids at stochastic nature of load demand and renewable energy resources using a modified capuchin search algorithm. Neural Comput. Appl. 35, 17645–17670. https://doi.org/10.1007/s00521-023-08623-9 (2023).
Hachemi, A. T., Sadaoui, F., Saim, A., Ebeed, M. & Arif, S. Dynamic operation of distribution grids with the integration of photovoltaic systems and distribution static compensators considering network reconfiguration. Energy Rep. 12, 1623–1637. https://doi.org/10.1016/j.egyr.2024.07.050 (2024).
Khan, N. H. et al. A novel modified artificial rabbit optimization for stochastic energy management of a grid-connected microgrid: A case study in China. Energy Rep. 11, 5436–5455. https://doi.org/10.1016/j.egyr.2024.05.018 (2024).
Author information
Authors and Affiliations
Contributions
S.Bharath—Research proposal—construction of the work flow and model—Final Drafting—Survey of Existing works—Improvisation of the proposed model; Dr. A. Vasuki—Initial Drafting of the paper—Collection of datasets and choice of their suitability—Formulation of pseudocode.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Bharath, S., Vasuki, A. Adaptive energy loss optimization in distributed networks using reinforcement learning-enhanced crow search algorithm. Sci Rep 15, 12165 (2025). https://doi.org/10.1038/s41598-025-97354-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-025-97354-z