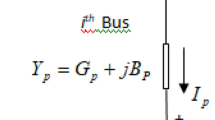Optimal allocation of hybrid PVDG and DSVC devices into distribution grids using a modified NRBO algorithm considering the overcurrent protection characteristics

Abstract

The never-ending issue of inadequate energy availability is constantly on the outermost layer. Consequently, an ongoing effort has been made to improve electric power plants and power system configurations. Photovoltaic Distributed Generators (PVDG) and compensators such as Distributed Static Var Compensator (DSVC) are the center of these recent advances. Due to its high complexity, these devices’ optimum locating and dimensions are a relatively new issue in the Electrical Distribution Grid (EDG). A modified version of Newton Raphson Based Optimizer (mNRBO) has been carried out to optimally allocate the PVDG and DSVC devices in tested IEEE 33 and 69 bus EDG. The mNRBO algorithm integrates four parameters to enhance NRBO’s performance by addressing its limitations in balancing exploration and exploitation. The article suggested novel Multi-Objective Functions (MOF), which have been considered to optimize concurrently the overall amount of active power loss (APL), voltage deviation (VD), relays operation time (TR_ELAY), as well as improve the coordination time interval (CTI) between primaries and backup relays set up in EDG. The proposed mNRBO algorithm surpasses its basic NRBO version, as long as another alternative algorithm, while providing very good results, such as minimizing the APL from 210.98 kW until 26.482 kW and 224.948 kW until 18.763 kW for the IEEE 33 and 69 bus respectively. Which proves the capability of the mNRBO algorithm of solving such power system challenges.

Introduction

General context

Over the past several decades, there has been a global emphasis on creating renewable energy sources (RESs) and integrating them into electrical power networks due to the growing need for energy¹. The International Energy Agency (IEA) predicts that by 2050, the global capacity will have reached 4674 GW².

Expanding the use of Renewable Energy Sources (RESs) requires distributed generation (DG). However, the erratic and unpredictable character of RESs can result in many severe problems with electricity quality. Consequently, several attempts have been made to address these problems by optimizing the placements and sizes of DG in the Electrical Distribution System (EDS).

Due to renewable energy’s intermittent and unpredictable nature, installation locations and the size of RES power plants must be carefully chosen and incorporated into EDS in optimum DG allocation studies³.

The ideal number and placement of DG units in a power system depend on several important variables. These elements are considered throughout the optimal DG allocation process to find the best configuration⁴. The ideal placement and size of DG units depend heavily on the load profile and power consumption patterns. By placing DG units close to buses with significant distribution system losses, optimal DG allocation can lower losses, enhance voltage profiles, and boost system efficiency.

Though system design and configuration are comparatively less important, Recent research on new distribution power systems focuses on system-wide investigations highlighting operational management methods and energy dispatch optimization. Studies have also been done on the centralized dispatch model, distribution network topology, and DG unit location and capacity determination⁵.

However, after incorporating DGs, the unidirectional power flow in traditional energy systems has changed to a bidirectional power flow. Variable power generation, excessive short circuit current, and an unwanted voltage rise can all result from bidirectional power flow⁶. Reverse power flow is enhanced by more and larger distributed generators (DGs) on the network, adversely affecting the coordination of protective relays configured and built for unidirectional power flow. For example, bidirectional power flow might impact relays’ fault current and tripping time settings, leading to inaccurate protection or prolonged disruptions⁷.

Motivation

Relays must be configured optimally under fluctuating fault current levels to provide enough and appropriate protection, avoid unintentional disruptions, and function immediately⁸. The main issue affecting electrical networks is short circuits. When there’s a short circuit in the transmission network, it can cause a sudden voltage drop, often leading to a voltage sag or dip. This may cause Distributed Generation (DG) units, such as solar, wind, or gas-powered generators, to detach or disconnect from the grid to protect themselves from potential damage. When DG units disconnect, it may result in a loss of power supply in the affected area. The consequences of this can be pretty significant, including voltage sag and grid stability issues.

Short circuit analyses should be used to verify the power transmission lengths of busbars and lines and their short circuit resistance capacity before DG integration to choose the appropriate protective equipment⁹. Additionally, in controlled islanding, islanding caused by short circuits should be regulated by regulating life safety and the system against dangers¹⁰.

Modern power systems use numerous renewable energy sources in addition to traditional generators. Power electronics are also the basis for various devices; one such example is the Flexible Alternating Current Transmission System (FACTS) devices, the most sophisticated reactive energy compensation devices available today¹¹.

Due to these issues and expenses, utilities engage in renewable energy, mainly photovoltaic distributed generation (PVDGs) or distributed static var compensator (DSVCs). These hybrid PVDG-DSVC units must meet strict technological and regulatory requirements for the distribution network to remain safe, stable, and effective. Reduced operation and maintenance costs of system components, enhanced dependability, maximized the benefits of renewable energy integration, minimizes power losses, enhances grid stability, and improves overall performance are the primary advantages of PVDG-DSVC units with EDSs. Poor placement can lead to inefficiencies, increased costs, and potential system instability, highlighting the importance of strategic placement for both economic and technical reasons¹².

State-of-the-art review

Recently, many optimization algorithms have been applied to find the optimum allocation of PVDG and DSVC in EDG, such as applying the External Particle Swarm Optimization algorithm (EPSO) to optimize some economic savings across different IEEE standard grids¹³, the Water Cycle Algorithm (WCA) to minimize multiple objective functions represented as power losses, voltage deviation, energy cost and pollution emissions in the IEEE 33, and 69 bus grids¹⁴, the Mutated Salp Swarm Algorithm (MSSA) to minimize the losses in active power¹⁵, the application of Improved Gey Wolf Optimizer (IGWO) to optimize the losses in power, voltage deviation and the investment costs in different standard distribution networks¹⁶.

The Constriction Factor Particle Swarm Optimization algorithm (CF-PSO) was also applied to optimize different objective functions of losses in active powers, voltage deviation and the voltage stability index across multiple standard networks of IEEE 33- and 136-bus¹⁷, an Improved Particle Swarm Optimization (IPSO) to minimize both of the voltage deviation and voltage harmonics in standard distribution systems¹⁸, also the Jellyfish Search Algorithm (JSA) to minimize losses in active powers and the pollution emissions, as an objective function¹⁹, The Slime Mould Algorithm (SMA) to reduce some objective functions represented as power losses, voltage deviation and cost of investment²⁰, applying the Bald Eagle Search Algorithm (BESA) to optimize the losses in power, the voltage deviation and stability index, along the heavy standard 118-bus²¹, and the Adaptive African Vultures Optimizer (AAVO) to optimize multiple objective functions of power losses, loading margin and voltage variation along the standard systems of IEEE 33, 85 and 141 bus²².

Main contributions

The Newton–Raphson-Based Optimizer (NRBO)²³ is an innovative optimization approach designed to tackle complicated optimization issues by combining Newton’s method with contemporary optimization methods. Historically, Newton’s method operates to identify the function roots by continually enhancing initial estimates using gradient data. This successfully guides the search for solutions. The Newton–Raphson Search Rule (NRSR) and the Trap Avoidance Operator (TAO), together with a few groups of matrices to further investigate the best results, are the two rules that the Newton–Raphson search rule algorithm uses to explore the complete search process.

Recently, there are several current Newton–Raphson method and algorithm implementations available in power system engineering topics for optimal droop-based islanded microgrid with DG integration²⁴, parameter extraction of photovoltaic cell models in six various models²⁵, graph attention network-based static voltage stability margin prediction technique²⁶, power harmonics parameters estimation²⁷, asymmetric multi-level inverter with selective harmonic reduction²⁸, calculate the incremental losses due to unbalanced operation for a given distribution system²⁹, the distribution network’s optimal impact on charging stations for electric vehicles³⁰, state estimate for railway power supply systems using pseudo-measurement techniques³¹, ideal load distribution issue for islanded microgrids taking frequency fluctuations into account³², optimal power flow with integrated electric power and natural gas system³³, and recently, optimal scalar speed control of the induction motors³⁴.

The objectives for operation in this article are contradictory. Consequently, determining which to allocate hybrid PVDG and DSVC is a complex multi-objective function (MOF) problem that must be addressed while balancing competing objectives. Yet, the primary findings made by this study may be summed up in the following points:

• Developing a modified NRBO algorithm to solve the formulated problem,

• Implementing different evaluations and benchmark tests to assess the proposed algorithm,

• Optimal planning of hybrid PVDG and DSVC devices,

• The MOF considers the overcurrent protection characteristics,

• The proposed methodology is implemented on two EDG test grids.

Structure of the paper

The article is structured as follows: Section"Modeling the hybrid system"conveys the modelling system parts; Section"Multi-objective design"is devoted to formulating the allocating issues; Section"Proposed newton–raphson-based optimizer (NRBO)"covers the assessment of the suggested method; Section"Application and optimized results"unveils its implementation and outcomes; and Section"Conclusion"finishes with a conclusion.

Modeling the hybrid system

Model of PVDG

The Probability Density Function (PDF) symbolizes a model of solar radiation over the entire day’s hours calculated using historical information³⁵. In the genuine investigation, the PDF for the solar radiation was established for each hour time frame as follows:

$${f}_{b}\left(s\right)=\left\{\begin{array}{c}\frac{\Gamma \left(A+B\right)}{\Gamma \left(A\right)\Gamma \left(B\right)}{s}^{(\alpha -1)} \quad 0\le s\le 1, A,B\ge 0\\ 0 \quad \quad Otherwise\end{array}\right.$$

(1)

Equations (2) and (3) define the parameters B and A as follows:

$$B=(1-\mu )\left(\frac{\mu (1-\mu )}{{\sigma }^{2}}-1\right)$$

(2)

$$A=\frac{\mu \times B}{1-\mu }$$

(3)

where σ and μ represent the average deviation and mean, accordingly³⁵. The probability of the solar radiation state at any point in time might be expressed as follows:

$${P}_{s}\left\{G\right\}={\int }_{{s}_{1}}^{{s}_{2}}{f}_{b}\left(s\right) ds$$

(4)

The PV panel’s power output may be expressed as follows^35,36:

$${P}_{{PV}_{^\circ }}\left(s\right)=N\times FF\times {V}_{y}\times {I}_{y}$$

(5)

$$FF=\frac{{V}_{MPP}\times {I}_{MPP}}{{V}_{oc}\times {I}_{sc}}$$

(6)

$${V}_{y}={V}_{oc}\times {K}_{v}\times {T}_{cy}$$

(7)

$${I}_{y}=s\left[{I}_{sc}\times {K}_{i}\times {(IT}_{cy}-25)\right]$$

(8)

$${T}_{cy}={T}_{A}+s\left(\frac{{N}_{OT}-20}{0.8}\right)$$

(9)

N is the module quantity, T_A and T_cy are the atmosphere and cell temperatures, and K_v and K_i tend to be the current and voltage the temperature values, accordingly N_OT represents the cell’s nominative temperature of operation, FF is the fill variable, and I_sc and V_oc are the short-circuit electrical current as well as the voltage in the open circuit, accordingly I_MPP and V_MPP denote the current state and voltage at MPPT, respectively.

The overall generated power of the solar panel is determined by the requirements and radiation features as follows:

$${P}_{PV}(t)={\int }_{{s}_{1}}^{{s}_{2}}{P}_{{PV}_{^\circ }}\left(s\right){P}_{s}\left\{G\right\} ds$$

(10)

Model of DSVC

Figure 1 shows the overall circuit framework of the DSVC^20,37. The DSVC is made up of a thyristor-controlled reactor and a permanent capacitor.

Fig. 1

DSVC device’s model: (a). Circuit framework, (b). Equivalent model.

The firing angle (α) of the thyristors determines the corresponding susceptance of the DSVC equipment (B_DSVC)³⁷. This may be conveyed in the following manner:

$${B}_{DSVC}={B}_{L}\left(\alpha \right)+{B}_{C}$$

(11)

$${B}_{L}\left(\alpha \right)=-\frac{1}{L.\omega }\left(1-\frac{2\alpha }{\pi }\right), {B}_{C}=C.\omega$$

(12)

B_C is capacitor reactance, and B_L remains the series induction reactance. C and L represent the capacitor’s capacity and the reactor’s inductance. Accordingly, V_j represents the voltage that exists at node j.

The DSVC gadget controls the reactive energy and current, as shown in the subsequent formulas:

$${Q}_{DSVC}=-{B}_{DSVC}.{V}_{J}^{2}$$

(13)

$${I}_{DSVC}=-{B}_{DSVC}.{V}_{J}$$

(14)

Whenever a system’s load is capacitance, the DSVC uses thyristor-controlled springs to absorb Q_DSVC; alternatively, if the system’s load is primarily inductive, the DSVC uses parallel-coupled capacitors to provide Q_DSVC, thereby improving voltage levels.

The formulated problem incorporates the appropriate limits of DSVC as part of the reactive power (capacitive or inductive) operation:

$${-Q}_{DSVC}^{max}\le {-Q}_{DSVC}\le {+Q}_{DSVC}^{max}$$

(15)

where –Q_DSVC^max and + Q_DSVC^max represent the DSVC’s introduced reactive power restricts (capacitive or inductive functioning modes, accordingly).

Multi-objective design

Multi-objective functions

The Multi-Objective Function (MOF) was designed to effectively find and dimension either PVDG and DSVC components within both EDG through reducing simultaneously and concurrently the technical parameters such as overall Active Power Loss (APL), overall Voltage Deviation (VD), overall Operating Time of the overcurrent relays (T_RELAY), and the overall Coordination Time Interval (CTI) between the installed relays. The MOF could be established as follows:

$$MOF=Minimize\left[\left({\sum }_{i=1}^{{N}_{Bus}}{\sum }_{j=2}^{{N}_{Bus}}{APL}_{i,j}+{\sum }_{j=2}^{{N}_{Bus}}{VD}_{j}+{\sum }_{i=1}^{{N}_{PR}}{T}_{RELAY,i}+ {\sum }_{i=1}^{{N}_{PR}}{\sum }_{i=j}^{{N}_{BR}}{CTI}_{i,j}\right)\right]$$

(16)

The APL³⁸, could be formulated as follows:

$${APL}_{i,j}={\alpha }_{ij}\left({P}_{i}{P}_{j}+{Q}_{i}{Q}_{j}\right)+{\beta }_{ij}\left({Q}_{i}{P}_{j}+{P}_{i}{Q}_{j}\right)$$

(17)

And,

$${\alpha }_{ij}=\frac{{R}_{ij}}{{V}_{i}{V}_{j}}\text{cos}({\delta }_{i}-{\delta }_{j})$$

(18)

$${\beta }_{ij}=\frac{{R}_{ij}}{{V}_{i}{V}_{j}}\text{sin}\left({\delta }_{i}-{\delta }_{j}\right)$$

(19)

R_ij represents the line’s resistance, and N_bus denotes the number of buses. (δ_i, δ_j) and (V_i, V_j) represent the angles and voltages, accordingly. (P_i, P_j) and (Q_i, Q_j) denotes active and reactive powers, respectively.

The VD³⁹, might be formulated as follows:

$${VD}_{j}=\left|1-{V}_{J}\right|$$

(20)

The T_RELAY could be formulated as in^40,41. For this research we have selected the characteristic of Normal Inverse, based on the standard IEC 60,255–3.

$${T}_{RELAY}=TDS.\left(\frac{A}{{M}^{B}-1}\right)$$

(21)

$$M=\frac{{I}_{F}}{{I}_{P}}$$

(22)

$${I}_{F}=\frac{{V}_{F}}{{Z}_{F}}$$

(23)

where T_RELAY represents the relay operating time, and TDS denotes the time dial setting. The relay constants, A and B, have been adjusted to 0.14 and 0.02, accordingly. M is a multiple of pickup current. I_F and I_P denote the fault and pickup current, accordingly. V_F represents the faut voltage magnitude, Z_F is the line impedance where the fault current occurred. Also, N_PR represents the quantity of primaries overcurrent relays, and N_BR represents the quantity of backups overcurrent relays.

The Coordination Time Interval (CTI) between primaries and backups OCRs could be represented as⁴¹:

$$CTI={T}_{RELAY-Backup}-{T}_{RELAY-Primary}$$

(24)

The constraints of equality

Equality constraints could be defined through the equilibrium powers formulas below:

$${P}_{Sub-station}+{P}_{PVDG}={P}_{Load}+APL$$

(25)

$${Q}_{Sub-station}+{Q}_{DSVC}={Q}_{Load}+RPL$$

(26)

P_Sub-station and Q_Sub-station represent the sub-stations overall active/reactive powers. P_Load and Q_Load represent the overall active/reactive load demand power. APL and RPL constitute the EDS loss of power. P_PVDG and Q_DSVC are the resulting powers generated by PVDG and DSVC units, accordingly.

The constraints of inequality

The unequal constraints over distribution systems could be established as follows:

$${V}_{min}\le \left|{V}_{i}\right|\le {V}_{max}$$

(27)

$$\left|{1-V}_{j}\right|\le \Delta {V}_{max}$$

(28)

$$\left|{S}_{ij}\right|\le {S}_{max}$$

(29)

V_min and V_max represent the min and max limits of bus’s voltage, respectively. ΔV_max represents the max drop in voltage. S_ij and S_max denote the apparent electrical power in the power distribution line as well as the highest level of it, accordingly.

The constraints for PVDG and DSVC devices

The constraints for hybrid PVDG and DSVC devices may be expressed as below:

$${P}_{PVDG}^{min}\le {P}_{PVDG}\le {P}_{PVDG}^{max}$$

(30)

$${Q}_{DSVC}^{min}\le {Q}_{DSVC}\le {Q}_{DSVC}^{max}$$

(31)

$$\sum_{i=1}^{{N}_{PVDG}}{P}_{PVDG}(i)\le \sum_{i=1}^{{N}_{bus}}{P}_{Load}\left(i\right)$$

(32)

$$\sum_{i=1}^{{N}_{DSVC}}{Q}_{DSVC}(i)\le \sum_{i=1}^{{N}_{bus}}{Q}_{Load}\left(i\right)$$

(33)

$${2\le PVDG}_{Position}\le {N}_{bus}$$

(34)

$${2\le DSVC}_{Position}\le {N}_{bus}$$

(35)

$${{N}_{PVDG}\le N}_{PVDG.max}$$

(36)

$${{N}_{DSVC}\le N}_{DSVC.max}$$

(37)

$$n_{PVDG,i} /Location \le 1$$

(38)

$$n_{DSVC,i} /Location \le 1$$

(39)

where (P_PVDG^min, Q_DSVC^min) represents the minimum power output delivered by PVDG and DSVC, accordingly. (P_PVDG^max, Q_DSVC^max) represent the maximum power delivered by PVDG and DSVC, accordingly (N_PVDG, N_DSVC) represent the PVDG and DSVC devices numbers, accordingly. (n_PVDG, n_DSVC) represent the positions of PVDG and DSVC devices on bus i, accordingly.

Tested distribution grids

Many standard evaluation grids, including the IEEE 33-bus and 69-bus EDG, as mentioned in Fig. 2⁴², were employed to gauge the efficacy of comparable NRBO and mNRBO algorithms. In electric power systems, testing grids are frequently used to benchmark and compare optimization algorithms.

Fig. 2

Single line diagram of tested distribution grids: (a). IEEE 33-bus, (b). IEEE 69-bus.

The IEEE 33-bus grid consists of 33 buses and 32 branches, with a combined load of 3715.00 kW and 2300.00 kVar. The IEEE 69-bus grid comprises 69 buses and 68 branches, with a combined load of 3790.00 kW and 2690.00 kVar. The nominal and standard voltage for tested grids is 12.66 kV.

These test grids’ buses are safeguarded via an overcurrent relay, with the initial test grid requiring 32 relays while the subsequent tested grid requires 68 relays.

Insofar as the fundamental network is represented via an unchanged power load, load variation must be simulated frequently to examine load fluctuations. The efficacy of each of the applied algorithms in solving the optimum power flow problem must be evaluated with these conventional test grids.

The optimal power flow issue aims to identify the ideal point of functioning over a power system by enhancing production and load distribution while meeting numerous requirements such as power balance, voltage limitations, and device operational constraints. Multiple indicators of performance have been employed to assess the algorithm’s effectiveness.

The results from these assessments may provide useful insights into the algorithms’ shortcomings and advantages. Assisting researchers as well as practitioners in determining the most effective technique for a given problem.

Proposed newton–raphson-based optimizer (NRBO)

Newton–raphson-based optimizer (NRBO)

The Newton–Raphson-Based Optimizer (NRBO) is a new metaheuristic technique prompted by Newton–Raphson’s technique²³. It examines the complete search procedure by employing the Newton–Raphson Method (NRM) to identify the search region via several vector puts of: the Newton–Raphson Search Rule (NRSR) as well as the Trap Avoidance Operator (TAO), in addition to some sets of matrices to investigate the most effective outcomes more thoroughly.

Newton–raphson method (NRM)

Newton’s approach, referred to the Newton–Raphson Method (NRM), serves as a root-finding process which locates the base of a function f(x) by using the initial few elements of its Taylor Series (TS) in the vicinity of an assumed root.

NRM is essentially akin to Horner’s approach to polynomials, such as f(x). The NRM begins at an initial location (x₀) then uses the TS assessed at x₀ to find an additional point close to the original solution. The process continues till a suitable solution has been identified. The TS of f(x) about the point (x = x₀ + ∈) is depicted as following.

$$f\left({x}_{0}+\in \right)=f\left({x}_{0}\right)+f^{\prime}\left({x}_{0}\right)\in +\frac{f^{{\prime}{\prime}}\left({x}_{0}\right){(\in )}^{2}}{2!}+\frac{f^{{\prime}{\prime}{\prime}}\left({x}_{0}\right){(\in )}^{3}}{3!}+\dots$$

(40)

$$f\left({x}_{0}+\in \right)\approx f^{\prime}\left({x}_{0}\right)\in +\frac{f^{{\prime}{\prime}}\left({x}_{0}\right){(\in )}^{2}}{2!}$$

(41)

The formula (42) may be used to determine the offset ∈ needed to get nearer than the root starting from x₀. Assume f(x₀ + ∈) = 0 and Eq. (42) solved for ∈ ≡ ∈₀ gives:

$${\in }_{0}=\frac{f^{\prime}\left({x}_{0}\right)}{f^{{\prime}{\prime}}\left({x}_{0}\right)}$$

(42)

Equation (43) represents the second-degree adjustment to the root’s location. When permitting x₁ = x₀ + ∈₀, find the subsequent location of the root and recite the process up until it merges to the optimum root employing Eq. (44).

$${\in }_{n}=\frac{f^{\prime}\left({x}_{n}\right)}{f^{{\prime}{\prime}}\left({x}_{n}\right)}$$

(43)

Unfortunately, this procedure may be disproportionate close to a local peak or horizontal asymptotic. However, the approach may be used repeatedly to identify the subsequent approximate with the correct starting point.

$${x}_{n}+1={x}_{n}-\frac{f^{{\prime}}\left({x}_{n}\right)}{f^{{\prime}{\prime}}\left({x}_{n}\right)}, n=1, 2, 3 \dots$$

(44)

In NRM, a rough zero (x₀) was an initial location that guarantees the algorithm’s secure convergence.

Initialization

Consider a particular situation: The optimization is carried out using an unencumbered single-objective optimization issue via a next specification.

$$Minimize :f({x}_{1},{x}_{2}, {x}_{3},\dots , {x}_{n})$$

$$lb\le {x}_{j}\le ub, j=1, 2, \dots ,dim$$

(45)

f(x) is the function of fitness that needs to be reduced, x_j is the decision vector, dim is the issue’s dimension, lb indicates the lower bounds, and ub reflects the upper bounds.

Similar to additional metaheuristic computations, NRBO begins its search over the optimum outcomes by generating initial random populations within the boundaries of the potential options. Given the assumption which there are multiple N_p populations, every single one which contains dim decision variables/vectors. Thus, the random population is created via Eq. (46).

$${x}_{j}^{n}=lb+rand\times \left(ub-lb\right), n=1, 2, \dots , {N}_{P} \ and\ j=1, 2, \dots , dim$$

(46)

xⁱ_j is the position of j^th dimension of n^th population, rand represents the random number along (0,1). Equation (47) denots the population matrix which may portray the populations in all dimensions.

$${X}_{n}=\left[\begin{array}{ccc}{x}_{1}^{1}& {x}_{2}^{1} \cdots & {x}_{dim}^{1}\\ \vdots & \ddots & \vdots \\ {x}_{1}^{Np}& {x}_{2}^{Np} \cdots & {x}_{dim}^{Np}\end{array}\right]$$

(47)

Newton–Raphson search rule (NRSR)

The NRSR controls the vectors, resulting in more precise exploration of a viable area and improved positioning. The NRSR depends on the concept of how the NRM is put forward to encourage exploration and accelerate convergence. Because many methods of optimization aren’t distinguishable, the concept of NRM is employed to substitute the written description of the function in these cases.

The NRM starts out with an assumed initial solution and moves on to a subsequent place in a specific path. To obtain the NRSR via Eq. (45), the second order derived has to be determined with the TS. The TS for f (x—Δx) and f (x + Δx) is presented as next.

$$f\left(x+\Delta x\right)=f\left(x\right)+{f}^{\prime}\left({x}_{0}\right)\Delta x+\frac{1}{2!}{f}^{{\prime}{\prime}}\left({x}_{0}\right){\Delta x}^{2}+\frac{1}{3!}{f}^{{\prime}{\prime}{\prime}}\left({x}_{0}\right){\Delta x}^{3}+\dots$$

$$f\left(x-\Delta x\right)=f\left(x\right)-{f}^{\prime}\left({x}_{0}\right)\Delta x+\frac{1}{2!}{f}^{{\prime}{\prime}}\left({x}_{0}\right){\Delta x}^{2}-\frac{1}{3!}{f}^{{\prime}{\prime}{\prime}}\left({x}_{0}\right){\Delta x}^{3}+\dots$$

(48)

Trap avoidance operator (TAO)

The TAO was added to enhance the efficiency of the proposed NRBO for dealing with real-world issues, which constitutes an altered and improved operator. The position of x_n^IT+1 can be significantly changed through the use of TAO. It generates a solution of higher quality X_TAO^IT through the combination of the ideal position X_b and the present vector location. X_n^IT. The solution X_TAO^IT is generated if the number of rand is lesser than Deciding Factor (DF) employing Eq. (49).

$${x}_{n}^{IT+1}={x}_{TAO}^{IT}$$

(49)

rand is a standard number that occurs among (0,1), θ₁ and θ₂ are standard random numbers among (1, 1) and (0.5, 0.5), respectively, DF represents the deciding factor that manages the NRBO efficacity, μ_1, and μ₂ are random numbers, and it is generated employing Eq. (50) and Eq. (51), respectively.

$${\mu }_{1}=\left\{\begin{array}{c} 3\times rand, \quad if \ \Delta <0.5\\ 1, \quad \quad \quad Otherwise\end{array}\right.$$

(50)

$${\mu }_{2}=\left\{\begin{array}{c}rand, \quad if \ \Delta <0.5\\ 1, \qquad Otherwise\end{array}\right.$$

(51)

Modified NRBO (mNRBO)

Despite the NRBO technique being a strong metaheuristic, it, like other optimization methods, may suffer from early convergence when tackling intricate optimization issues. This is undesirable since it gets trapped at a local optimum rather than identifying the optimal global solution to that issue. Local optimum traps tend to occur due to insufficient exploration of searching space.

In optimizing, exploration implies searching extensively throughout the solution space in search of various areas that might hold better solutions. In contrast, exploitation relates to improving potential solutions after they have been discovered. The mNRBO algorithm improves NRBO’s achievement by tackling its drawbacks in managing exploration and exploitation: linear time operator (ω), enhanced encircling phase of RSA with Gaussian mutation, chaotic local search (CLS), and improved solution reliability of the RUN algorithm.

Linear time operator (${\varvec{\omega}}$)

The created strategy employs an interim operator to accomplish an excellent balance of exploration and exploitation. The Transition Operator, shortened as ω, may be determined as shown in Eq. (52):

$$\omega =\text{exp}(-\frac{t}{T})$$

(52)

t is the present iteration, and T is the highest and maximum iteration.

Enhanced encircling phase of RSA with gaussian mutation

Large step motion during the exploration phase is necessary to cover the search space. However, NRBO’s exploration phase falls short in this regard because it updates agent positions solely based on the best agent in the swarm and their current location, which prevents the agents from moving in large steps across the given region. In this part, we suggest the following exploration phase based on the Reptile Search Algorithm (RSA).

Good exploration strategies are based on the random selection of agents incorporated with Gaussian mutation and linear time operator. Gaussian mutation shows superior local search capabilities since it has a more focused mutation operator. The updated solution is given by:

$${X}_{t+1,j}=\left\{\begin{array}{c}\begin{array}{cc}{X}_{r2,j}+\omega *Gaussian(\text{0,1})*\left|{X}_{best,j}-{X}_{t,j}\right|& t<T/4\end{array}\\ \begin{array}{cc}{X}_{r2,j}+\omega *Gaussian\left(\text{0,1}\right)*\left({X}_{best,j}-{X}_{t,j}\right)-\beta *r*R& t<\frac{T}{2}\&t>T/4\end{array}\\ \begin{array}{cc}{X}_{best,j}& otherwise\end{array}\end{array}\right.$$

(53)

$${R}_{i,j}=\frac{{X}_{best,j}-{X}_{r1,j}}{{X}_{best,j}+\varepsilon }$$

(54)

$\beta ={e}^{-3}$, $r$=rand [0,1], j is the dimension, r₁ and r₂ are two random selected agents.

Chaotic local search (CLS)

Combining chaotic dynamics with a local search strategy and allowing an additional search in the neighboring area can enhance the effectiveness of the optimization process by facilitating more thorough exploration of the solution space.

This approach is particularly useful in complex optimization problems where finding the global optimum or near-optimum solutions is challenging. The Chaotic local search (CLS) is given by:

$${X}_{t+1}=\left(1-\omega \right).{\text{X}}_{\text{best}}+\omega .{C}_{r}$$

(55)

$${C}_{r}=LB+rand.\left(UB-LB\right)$$

(56)

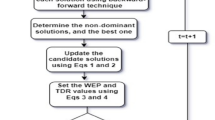
Algorithm 1. Pseudo code of the proposed mNRBO algorithm.

Experimental

Benchmark validation

This part demonstrates the significance of the mNRBO algorithm in optimization problems. It applies the algorithm to a range of test functions and proves its superior performance using a set of evaluation measures.

Benchmark description

As part of our research, we tested our mNRBO algorithm with some tricky optimization problems called CEC2022 test suites⁴³. These problems come in four types: unimodal, multimodal, hybrid, and composite functions.

The settings for the test are the number of iterations equal to 1000, and the number of populations being 50 in each try. To be sure of the results, we did this test with 30 independent runs. We looked at the average and the varied results. The best results are shown in bold.

Table 1 describes these functions’ names, search ranges, optimum values, and dimensions (dim). Furthermore, Fig. 3 visualizes the search spaces of some random benchmark functions.

Table 1 Specifics about the benchmark functions.

Fig. 3

CEC’2022 benchmark functions.

Testing results and discussion

Statistical results

Table 2 shows each algorithm’s final ranking, standard deviation, best, worst, and mean based on 30 independent runs on the 12 CEC’2022 benchmark functions.

Table 2 Comparison of different algorithms in solving the benchmark functions.

Based on the analysis of the table, the best answer marked in bold demonstrates that mNRBO demonstrates superior performance in achieving optimal solution accuracy on a significant majority of the test problems.

Specifically, out of the 12 test problems evaluated, mNRBO achieves optimal solutions in 10 cases. This indicates that mNRBO algorithm possesses robust and competitive search capabilities compared to other methods that were likely evaluated alongside it in the study.

Lastly, the nonparametric Wilcoxon test⁴⁴ was used to compare the approaches, with a significance threshold of 0.05. Table 3 showed statistically significant differences of mNRBO compared to other algorithms presents the statistical findings. This performance superiority was consistent across various comparisons, indicating that the mNRBO method proposed in the study outperforms others and demonstrates the best overall performance.

Table 3 p-value of Wilcoxon sum test between mNRBO and its competitors.

Convergence analysis

The convergence curves in Fig. 4 demonstrate how mNRBO compares with competing algorithms in achieving optimal solutions over iterations. mNRBO consistently showed faster convergence towards near-optimal solutions compared to its competitors across various benchmark functions.

Fig. 4

Convergence curves of mNRBO algorithm with competitors.

Specifically, in a comparison across twenty test functions, mNRBO exhibited the fastest convergence in ten cases, highlighting its superior performance in solving these optimization problems.

Boxplot analysis

Boxplots provide a clear visual representation of data distribution and variability. In the context of comparing algorithm performance, Fig. 5 shows narrower boxplots for the mNRBO algorithm indicate less variability and potentially more consistent performance across multiple benchmark functions.

Fig. 5

Boxplots of mNRBO algorithm with competitors.

Figure 6 represents the flowchart for the proposed mNRBO algorithm.

Fig. 6

Flowchart for mNRBO algorithm.

Application and optimized results

Following the completion of the section in which the performance of the mNRBO algorithm is evaluated and contrasted with different optimization methods, the outcomes show that the two algorithms NRBO and mNRBO algorithms accomplish the best achievement.

The mNRBO algorithm is proposed to handle more complex optimization problems, including those involving uncertainties like changing loads or the integration of Photovoltaic (PV) systems and DSVCs into power grids. For our proposed system where PV and DSVC devices are integrated, there can be significant variability in both generation and demand. The mNRBO can enhance robustness by adjusting its optimization process to better accommodate the nonlinear and dynamic nature of these systems. This includes refining the algorithm to respond to fluctuating power outputs from PV systems or varying load conditions. By incorporating additional considerations such as sensitivity to changing load patterns or real-time adjustments to DSVC settings, mNRBO offers greater flexibility and stability in optimizing grid performance.

To demonstrate its effectiveness and authority, we selected to carry on the application by solving a power system issue (Optimum PVDG-DSVC devices incorporation) and contrasting it to the identical methods used in the optimization part.

Tables 4 and 5 indicate the results of optimization employing the selected optimization techniques, contrasting the scenarios before and after the installation of PVDG and hybrid PVDG-DSVC devices in IEEE 33 and 69-bus EDG, accordingly.

Table 4 Optimized outcomes for the IEEE 33-bus.

Table 5 Optimized outcomes for the IEEE 69-bus.

Numerous simulations were performed via the MATLAB program to demonstrate the effectiveness of each of the chosen methods in producing the most favorable results for the two investigated EDG. The primary observation is that the mNRBO algorithm surpasses its fundamental variant as well as all other methods, resulting in the lowest Multi-Objective Function (MOF) scores of 54.569 and 74.381 for the two examined EDG, accordingly.

Furthermore, when speaking of every parameter on itself, the mNRBO algorithm delivered the ideal outcomes for all of them, along the hybrid PVDG-DSVC scenario. The previous debate verified the fact that mNRBO has been the most effective algorithm because, besides providing the successfully and minimum MOF scores, it additionally offered the ideal and lowest values of every parameter individually.

Whereas employing mNRBO algorithm for the optimum inclusion of hybrid PVDG-DSVC devices reduced APL until 26.482 kW and 18.763 kW, accordingly, the voltage deviation until 0.238 p.u. and 0.336 p.u., respectively, and the T_RELAY until the values of 20.149 s and 38.434 s for both IEEE 33 and 69 buses, accordingly, with the maintaining of the coordination time interval in its nominal limits.

Figures 7 and 8 show the convergence characteristics of MOF reduction using comparable techniques to optimize the incorporation of distributed units in the two tested grids.

Fig. 7

Convergence curves of the applied competitor algorithms for the IEEE 33-bus: (a). PVDG Case, (b). Hybrid PVDG-DSVC Case.

Fig. 8

Convergence curves of the applied competitor algorithms for the IEEE 69-bus: (a). PVDG Case, (b). Hybrid PVDG-DSVC Case.

Following numerous runs and applications, all comparable algorithms keep converging in fewer than 100 iterations to resolve the suggested power system issue, which is the justification for setting that maximum number of iterations. All algorithms performed well in terms of MOF reduction. In addition, the mNRBO showed faster convergence times across the studied cases and grids. It was clearly shown that the mNRBO surpassed the conventional NRBO algorithm.

The mNRBO algorithm achieved its highest fitness scores within its first iterations across all investigated cases owing to the enhancements provided by those versions of NRBO. Consequently, the mNRBO improved the NRBO algorithm’s efficiency, problem-solving ability, and convergence rate.

Figure 9 shows an analysis of the bus voltage levels in the fundamental case and the remaining investigated scenarios for the optimum incorporation into the two testing grids EDG according to the results acquired by the mNRBO algorithm.

Fig. 9

Voltage profiles with suggested cases for both tested grids: (a). IEEE 33-bus, (b). IEEE 69-bus.

Figure 8 depicts the impact of every studied scenario for the optimum incorporation on the voltage levels of the two tested grids. Following the integration of all of the studied scenarios, the voltage profiles enhanced nearly everywhere across both EDG’s buses.

Furthermore, outstanding outcomes and substantial enhancements were obtained when incorporating hybrid PVDG and DSVC components into either EDG. The effects and improvement have been linked to the reduction of voltage deviation until 0.238 p.u. and 0.336 p.u. in IEEE 33 and 69 bus EDG, respectively. Insofar as it demonstrates the actual amount of the EDG’s voltage and how far it deviates compared to the nominal voltage’s amount of 1 p.u.

Figure 10 depicts the influence of the optimum integration across all investigated scenarios on the active power loss variance for every single branch of both tested EDG.

Fig. 10

Active power losses with the suggested cases for both tested grids: (a). IEEE 33-bus, (b). IEEE 69-bus.

Given the axial structure for both of the tested distribution grids, active losses in power occur more frequently in most of the grids’ branches, making it vital to reduce them to accomplish a lot of techno-economic advantages.

The illustrations in Fig. 10 show that incorporating each scenario examined across both tested grids significantly minimized active losses in power nearly in every branch across both EDG.

The hybrid PVDG and DSVC devices produced the most effective outcomes in mitigating APL in every branch of the two EDG when they combined active and reactive powers.

The optimum incorporation of hybrid PVDG and DSVC devices additionally decreased overall active losses in power from 210.987 kW to 26.482 kW for the IEEE 33-bus and from 224.945 kW to 18.763 kW for the IEEE 69-bus.

Figures 11 show the difference in fault current between the scenarios before and after incorporating PVDG and DSVC devices into the two testing grids.

Fig. 11

Fault current variation after the suggested cases for both tested grids: (a). IEEE 33-bus, (b). IEEE 69-bus.

The optimum incorporation of all investigated scenarios has been noticed to have an immediate effect on fault current, boosting it across all buses over each of the tested grids, including the highest impact from the case of hybrid PVDG and DSVC devices. For instance, within the standard IEEE 33-bus, via buses 11 and 19, the fault current raised approximately 4.6 kA and 5.2 kA, respectively.

Furthermore, compared with the fundamental scenario for IEEE 69-bus, it’s observed that following the incorporation of hybrid PVDG and DSVC devices, the fault current jumped to approximately 140.11 kA and 84.50 kA in buses 18 and 69.

The setting up of PVDG and DSVC devices immediately affects the fault current across all buses over the two testing grids. The latter increases because of the inverse relationship between it and the bus voltage, which increases following the incorporation of investigated scenarios in the tested grids, as previously stated and due to the formula (23).

Figure 12 shows the disparity in primary overcurrent relay operating time across the fundamental scenario and the remaining examined scenarios with the optimum incorporation into both tested EDG.

Fig. 12

Relay’s operating time after suggested cases for both tested grids: (a). IEEE 33-bus, (b). IEEE 69-bus.

The primary function of overcurrent relays is to identify fault currents via lines and promptly isolate and safeguard the entire system. Reducing the operating time of those OCRs is both technically advantageous (protecting the system’s components) and economically profitable (extending the gadget’s lifetime).

The optimum implementation of every studied scenario using the mNRBO algorithm resulted in the reduction of operating time across all OCR set up in the two EDG standards, just like in Fig. 11 through ∆T_Relay. This reflects the disparity among each OCR’s operating time during the fundamental scenario and following every scenario investigated for optimum incorporation into both EDG.

Additionally, it becomes apparent that the incorporation of hybrid PVDG and DSVC devices was the most effective scenario for this reduction, resulting in an overall T_RELAY decrease from 20.574 s to 20.149 s over the initial standard EDG and from 38.772 s to 38.434 s for the subsequent standard IEEE 69-bus.

The effect was immediately associated with an upsurge in fault current, which was influenced by the boost of voltage levels stated in formulas (22 and 23). In this case, the OCR operates more quickly as the fault current rises.

Figure. 13 depicts the coordination time interval across the existing relays in the scenarios before and after incorporating PVDGs and DSVC devices into tested EDG.

Fig. 13

Coordination time interval after suggested cases for both tested grids: (a). IEEE 33-bus, (b). IEEE 69-bus.

The findings shown in Fig. 13 indicate that CTI dropped following the optimum incorporation of both studied scenarios into tested EDG stipulated through the mNRBO algorithm. The CTI was dropped across all systems’ primary and backup OCR, with respect to the permitted margins of the minimum CTI score of 0.2 s.

The decrease was caused by reducing the OCR’s primary operating time. Furthermore, it appears obvious that the optimum inclusion of hybrid PVDG and DSVC devices in the tested grids had the most significant impact on lowering CTI to 7.698 s and 16.717 s for both studied EDG, respectively.

Insofar as the CTI is regarded as the distinction between the primary and backup OCRs, reducing and maintaining it over the lowest permitted margin enhances the protection system by preventing miscoordination among the OCRs, as mentioned earlier.

Conclusion

The modified Newton Raphson-based optimizer algorithm significantly enhanced the reliability of electrical distribution grids. It successfully tailored the placement of hybrid PVDG and DSVC devices, decreasing active losses by up to 26.48 kW and 18.26 kW for the IEEE 33 and 69 bus systems, respectively.

The implementation of the mNRBO algorithm resulted in higher voltage levels throughout distribution grids after minimizing the voltage deviation until 0.238 p.u. and 0.336 p.u. for both tested IEEE 33 and 69 bus grids, which enhanced overall system resilience and accuracy, especially during peak load limitations.

Meanwhile, the protection system based on overcurrent relays can be improved by minimizing operating time and maintaining coordination within adequate limitations, extending equipment lifetime, system selectivity, and safe service continuity. Distribution grids benefited from decreased environmental impact by integrating hybrid PVDG and DSVC devices. They enhanced their capacity to cope with greater demands while preserving voltage stability, causing an essential move towards sustainable energy targets.

By retaining this information throughout the discovery procedure, the mNRBO algorithm ensures an ongoing exploration process, yielding superior outcomes compared to the original method and other comparable computations in terms of effectiveness and capacity to attain more minor multi-objective function rankings.

The convergence features demonstrated the following: overall optimized outcomes were obtained in a shorter period than the rest of the algorithms. The practical implementation of the mNRBO algorithm for hybrid device placement broadens new research avenues.

Prospective studies might investigate incorporating other renewable sources and battery storage, including charging stations for electric cars, and addressing various technological and financial obstacles to improve distribution grid performance and reliability.