Development of an integrated reactor model package for optimizing the operating modes of the sulfur production unit

Abstract

Complex technological systems in oil refining and other industries, consisting of numerous interconnected units, are often characterized by the uncertainty of initial information required for modeling and optimizing their operating modes. This study addresses the issue of uncertainty in the development of models for such technological systems with fuzzy input, operational, and output parameters, which remain relevant yet underexplored and unresolved. The paper proposes a concept for developing a model package of interconnected units for technologically fuzzy systems and describes the implementation algorithm of the proposed concept. Based on this algorithm, hybrid models of interconnected reactors in the sulfur production unit at the Atyrau refinery were developed, consisting of statistical, fuzzy, and linguistic models. These models allow the determination of the sulfur volumes produced in the reactors and their fuzzy quality indicators depending on the reactors’ operating modes. The developed models of interconnected reactors, including the Claus thermal reactor and Cold Bed Absorption, are combined into a single model package according to the sulfur production process and the technological scheme of the research object. The resulting model package enables systematic modeling of reactor systems and the selection of optimal operating modes. For this purpose, a software suite was created to simulate various operating modes of the reactor system on a computer to optimize their operation. The results of systematic modeling and optimization of the sulfur production unit demonstrate the advantages of the proposed approach compared to known methods.

Introduction

Oil refining production and the oil industry, in general, are the main sources of energy and driving forces of the economy of Kazakhstan and many other countries. However, these productions are also major sources of environmental pollution. Recently, due to the tightening of environmental standards for motor fuels and oil products¹, the task of optimizing the operating modes of oil refining technological objects based on economic and environmental criteria has become particularly relevant². It is known that the functioning of oil refining technological systems and the use of obtained oil products significantly deteriorate the environmental state. This is because oil refining processes release many harmful and toxic substances, such as hydrogen sulfide, carbon monoxide, nitrogen oxides, carbon dioxide, heavy metals, and other wastes, spreading into the atmosphere and contaminating soils³. These emissions from oil refining negatively impact human health and other living organisms⁴, poisoning them, and certain doses can be lethal⁵. Other oil refining wastes also pollute the environment, significantly worsening its ecological state.

The models being researched and developed in this work are the sulfur obtaining block (SOB) of the sulfur production unit (SPU) of Atyrau refinery are intended for collecting and processing hydrogen sulfides and other harmful gases from oil refining to produce a useful product—granular sulfur. нeфтeпepepaбoтки c цeлью пpoизвoдcтвa oт ниx пoлeзнoгo пpoдyктa − гpaнyлиpoвaннoй cepы. Such SPUs, which process sulfur-containing harmful gases emitted during oil refining and convert them into useful products, are operated not only at other oil and gas processing plants in Kazakhstan but also in other countries.

From sulfur, many demanded products are further produced, such as medicines, paints, gunpowder, pyrotechnics, road construction materials (sulfur asphalt, sulfur concrete), fertilizers for agriculture, and more.

In this proposed study, the problems of sulfur treatment processes have been identified, and an approach to solving them based on mathematical modeling methods has been justified. This approach is theoretically grounded and, with the help of computers, enables efficient and rapid control of sulfur production processes at SPUs. Thus, research on the development of mathematical models for the SOB, considering uncertainty in sulfur quality indicators, which is directly produced in the SOB, is particularly important and relevant for optimizing its operating modes. This is due to the fact that a priori models, which describe all processes and introduce noise, are insufficient for modeling sulfur production processes, as they do not account for the uncertainties in sulfur quality indicators. The relevance of developing a model package that incorporates available fuzzy information for optimizing SOB operating modes is increasing, as it allows for addressing both environmental and economic challenges faced by oil refining enterprises.

When developing models for poorly formalized, complex technological systems, challenges arise due to uncertainty caused by the stochastic nature and fuzziness of input data. To address these uncertainties, it is necessary to apply scientifically grounded methods, including: System analysis methodology, Expert evaluation methods,Fuzzy set theory⁶. The system analysis methodology, based on the integrated use of formal and informal methods, leverages artificial intelligence technologies, including fuzzy set theory methods, machine learning with neural networks, evolutionary algorithms, and other approaches. The synergistic effect of combining these methods enables a more effective resolution of uncertainties when studying and developing models for complex systems.

Fuzzy modeling methods for poorly formalized complex objects are based on fuzzy set theory, incorporating expert evaluation methods. Expert evaluation methods are used to collect and formalize fuzzy information, which represents the knowledge, experience, and intuition of domain experts in the given field. The obtained fuzzy information is then processed using fuzzy set theory methods, implementing operations on fuzzy sets through membership functions, which formalize the collected fuzzy information for computational processing.

With the increasing share of sulfurous and high-sulfur oils, the tasks of improving the efficiency of the sulfur production unit at oil refineries, strictly adhering to environmental standards and reducing their impact on the environment, are of primary importance. The most effective approach to solving these tasks is scientifically grounded methods based on modern mathematical methods (modeling and optimization) using the capabilities of information technology methods and tools. Solving these tasks in practice is complicated by the complexity of oil refining objects, as they consist of many interconnected units with numerous interrelated parameters affecting their operating modes and quality. Additionally, optimization tasks for oil refining technological systems based on their models must be carried out according to a vector of economic and environmental criteria, complicating the processes of model development and optimization. Moreover, when developing models and optimizing the sulfur production unit and other objects, additional problems arise in practice related to the lack of necessary initial information and its fuzziness⁶. For example, important parameters of the sulfur production process that determine the quality of the target product (sulfur color, mass fraction of sulfur, ash, organic substances, and water in the product) are not measured by instruments. These important indicators defining sulfur quality are determined by production personnel (technologists, operators, laboratory specialists) based on their experience, knowledge, and intuition in natural language, i.e., they are fuzzy. All this motivates the conduct of this study dedicated to the development of models for complex technological systems, exemplified by the sulfur production unit in oil refining, allowing through systematic modeling to optimize its operating modes by a vector of criteria under conditions of information deficit and fuzziness. Furthermore, the motivation for conducting this study was the lack of a formalized methodology and a concept for developing a package of interconnected models for technological system units in existing research.

It is known that production objects often operate under uncertainty due to the random or fuzzy nature of their technological parameters characterizing their operation. The randomness of their values arises due to various interferences, deviations in measurements, etc. The cause of the fuzziness of their values is that some parameters are immeasurable and can be estimated by the human operator, production personnel, based on their experience, knowledge, and observations fuzzily in natural language, i.e., they are fuzzy information. In case of randomness of parameter values, uncertainty problems can be solved using probabilistic methods⁷ and mathematical statistics methods⁸. If parameter values are estimated fuzzily⁹, then to solve the uncertainty problem¹⁰, it is necessary to apply expert evaluation methods¹¹ and the mathematical apparatus of fuzzy set theory¹².

Fuzzy methods can also effectively solve uncertainty problems due to the random nature of parameter values since often the collection and processing of statistical data on the operation of production objects turn out to be very complex and economically impractical. This position justifies the practical importance and relevance of developing a model package of interconnected units of technologically fuzzy systems used to optimize their operating modes and motivates the necessity of conducting this study.

Thus, the aim of this study is to create a concept for developing a model package of technological system units based on a systematic approach using available diverse information, allowing to optimize their operating modes. Based on the created concept, using available statistical and fuzzy information, a model package of reactors of the sulfur production unit at the Atyrau refinery will be synthesized, allowing to optimize its operating modes.

In recent times, research on the development of models for complex technological systems and the optimization of their parameters using developed models has intensified¹³. Ostrovsky et al., in¹⁴, studied the methodology for modeling technological systems and the optimization of chemical-technological system design, considering random constraints through an iterative approach. The issues of dynamic modeling and optimization of industrial sulfuric acid plant processes were explored in¹⁵. In their study, Anqi¹⁶ proposed an approach to optimizing the process of reducing environmental pollution in sulfur production processes using machine learning. Additionally, Khan et al.¹⁷ investigated forecasting and optimization of SPUs using machine learning techniques.

Under the guidance of Ghahraloud and Mounaam, modeling and optimization of the industrial sulfur production process at the Claus unit¹⁸ and optimization issues of the sulfur burning unit at oil refineries¹⁹ were conducted. The authors of²⁰ proposed approaches to optimizing the parameters of a high-sulfur gas purification plant, and in²¹ the issues of environmental optimization of sulfur production technology were investigated. However, in the analyzed above and many other studies, the conditions for the availability or accessibility of initial information for model development and optimization process were considered, i.e., deterministic conditions. In addition, they have not sufficiently studied the solutions to the problems of developing a package of models of interconnected units.

In the analyzed works and some other studies, approaches to developing models²² and optimization considering process dynamics and uncertainty due to the random nature of some parameters were investigated²³. However, they did not consider the problems of developing mathematical models for optimizing the operating modes of technological systems such as the sulfur production unit, whose product quality parameters are described fuzzily. And in the optimization, only a single-criteria situation is assumed, i.e., optimizing the operating modes of units and the sulfur production unit is carried out only by one criterion. Several studies have explored the problems of multi-criteria optimization in sulfur production processes and proposed approaches to their solution. For example, in²⁴, approaches to solving the multi-criteria optimization problem of the thermal section in the Claus process were investigated using a kinetic model. In²⁵, the oxidation process of sulfur dioxide was optimized based on multiple criteria using model-based approaches. Shang et al.²⁶ proposed an approach to multi-objective optimization of high-sulfur gas purification plants, while²⁷ explored the multi-objective optimization of sulfur recovery processes using a reaction mechanism to reduce energy consumption.

However, in these and other works, attention is not paid to the problems of fuzziness of some parameters of multi-criteria optimization tasks (e.g., criteria constraints, etc.) and the contradiction of these criteria in the effective solution domain. In such cases, it is necessary to formulate the multi-criteria optimization tasks as decision-making problems in a fuzzy environment and develop methods for solving them.

Additionally, in the analyzed studies and existing research, the formalization of a methodology and the concept of developing a package of interconnected models for technological system units has not been sufficiently considered or explored. This gap in research also motivated the current study, which aims to formalize and develop a concept for creating a package of interconnected models for the main units of a technological system. Such an approach enables the synthesis of a model package for complex systems, facilitating their efficient modeling and optimization.

Thus, it is extremely necessary to develop methods for model development and solving multi-criteria optimization tasks, i.e., decision-making based on economic and environmental criteria under conditions of fuzzy initial information or its part. The proposed work develops precisely the methods for developing a package of interconnected models of complex fuzzy described objects on the example of the sulfur production unit and decision-making methods for selecting optimal operating modes based on fuzzy and available information of other nature.

Materials and methods

The object of study in this work is the reactors of the SOB sulfur production unit (SPU) at the Atyrau refinery, which belongs to a complex technological system consisting of many interconnected and interacting units. The quality of the sulfur produced is characterized by fuzziness. To optimize the sulfur production process under these conditions, it is necessary to develop a package of interconnected models of the main SOB units, taking into account the fuzziness of some of the initial information, allowing for systematic modeling and finding the optimal operating mode. The SOB reactor model package is created by integrating the developed models of reactors and condensers, considering the sulfur production process occurring within them and aligning with the technological scheme of the SPU.

The materials used in the study include available data on the object of study and its operating modes: theoretical information, experimental-statistical data, fuzzy information obtained from expert specialists and decision makers who manage the sulfur production process, such as operator-technologists. Additionally, the concept of developing a package of models of technological system units based on a systematic approach, created in this work, is used. This concept is applied to synthesize a package of interconnected models of reactors and other SPU units used to optimize their operating modes.

The proposed systematic approach to modeling complex systems, based on the developed concept, is applied to synthesize a package of interconnected models for reactors and other SOB units under uncertainty conditions arising from the stochastic and fuzzy nature of input data. This systematic approach is based on fuzzy set theory, system analysis methodology, and expert evaluation methods, which are theoretically justified by their respective theorems, such as the theorem on the adequacy of fuzzy models²⁸ and the theorem on the convergence of expert opinions²⁹.

For effective identification of the membership function structure, the following adaptive formula is proposed:

$$\mu_{{B_{j} }}^{t} \left( {\tilde{y}_{j} } \right) = exp\left( {Q_{{\tilde{B}_{j} }}^{t} \left| {\left( {y_{j} - y_{j}^{md} } \right)^{{N_{{\tilde{B}_{j} }}^{t} }} } \right|} \right).$$

In this nonlinear dependence:

• t –is the term number in the term set, describing the variation of the fuzzy parameter.

• ${Q}_{{\widetilde{B}}_{j}}^{t}$- is the coarse-tuning parameter, identified at the α = 0.5 level, which allows for rapid adaptation of the function to the membership function graph.

• ${N}_{{\widetilde{B}}_{j}}^{t}$– is the fine-tuning parameter, enabling slow but more precise approximation of the membership function graph.

• ${y}_{j}^{md}-$ is the variable that most accurately corresponds to the selected term, determined by the condition: ${\mu }_{{\widetilde{B}}_{j}}\left({\widetilde{y}}_{j}\right)=\underset{j}{\text{max}}{\mu }_{{\widetilde{B}}_{j}}^{t}\left(\widetilde{{y}_{j}}\right).$

The proposed membership function structure is universal and, by adjusting the tuning parameters, allows for the construction of a more adequate function for different values of fuzzy parameters. In the proposed concept for developing a package of interconnected models for technological system units based on a systematic approach, this structure is used for defining membership functions in the fuzzy model development process.

We present the technological system of the SPU at the Atyrau refinery and describe the basis of the granular sulfur production process according to the technological scheme of the object of study, shown in Fig. 1.

Fig. 1

Technological diagram of the sulfur production unit of Atyrau SPU refinery.

A sulfur production installation with a capacity of 26 tons per day, utilizing hydrogen sulfide from sour gases based on Claus and Cold Bed Absorption (CBA) reactor technology, is one of the new units at the Atyrau refinery. The feedstock for the SPU is hydrogen sulfide contained in the sour gas obtained after amine regeneration and stripping of sour water.

A saturated hydrogen sulfide amine solution from other refinery units is supplied. Liquid hydrocarbons from the upper layer of the amine solution are periodically drained through hydrocarbon traps into the underground tank 31-D-003 as they accumulate. Carbon vapors containing sour gas (H₂S) are directed to the reflux drum 31-D-002 (see Fig. 1). In the regenerator 31-V-001, the dissolved hydrogen sulfide is stripped from the amine solution.

Due to the difference in density, non-evaporated liquid carbons are separated from the water and, as they accumulate, are manually removed from the middle part of the reflux tank 31- D-002 through the oil product separator into the buried tank 31—D-003.

To maintain the necessary concentration of the amine solution, fresh amine solution is supplied to the separator 31-D-002 when levels decrease due to water being carried away with the acid gas. The regenerated amine solution from the bottom of the regenerator 31-V-001 sequentially enters the inter-tube space of the condenser 31-E-002, where it is cooled by a counterflow of the saturated amine solution. The amine solution from the separator 31-D-003 is fed into the separator 31-D-002 to replenish the system.

The following main stages of the technological process for sulfur production have been identified:

• 1. The Claus thermal conversion stage, where acid gas flows are burned in the main burner of the 33—F -001 thermoreactor.

• 2. The Claus catalytic conversion stage takes place in a Claus 33—R-001 reactor in the presence of a catalyst on an aluminum oxide carrier.

• 3. The stage of liquefaction of sulfur obtained at the stage of thermal and catalytic conversion is carried out in a sulfur condenser 33—E-001.

• 4. The conversion step in CBA reactors is a cyclic process that uses a catalyst to both promote the reaction ${2\text{H}}_{2}\text{S}+{\text{SO}}_{2}\to 2{\text{H}}_{2}+3/8{\text{ S}}_{8}$ and adsorb the sulfur produced. The process takes place in reactors CBA 33—R-002, 33—R-003 . Regeneration of the activity of the CBA catalyst is carried out by supplying hot process gas from the Claus 33- R-001 reactor to heat the catalyst and desorption of sulfur, followed by its condensation in the 33-E-002 condenser.

• 5. Sulfur degassing stage. The main parameter of the degassing process is the duration of stay of sulfur in the degassing compartment of the sulfur pit 33-TK-001, from where liquid sulfur is sent to the crystallization unit and production of granulated sulfur. And the released H₂ S from 33-TK-001 is disposed of in waste incinerator 33- F-002 ( see Fig. 1 ).

The volume of sulfur produced and its quality indicators depend on the values of the input, operating parameters, the described main units of the SPU reactors R³⁰, separators D , condensers E and furnace F those. on their operating modes³¹ . In this regard, in order to make decisions on choosing the optimal operating mode of the SPU, a package of models of its main units should be developed, describing the dependence of the quantity and quality of sulfur on the values of input and operating parameters . Then, by implementing these models in software through computer modeling of various operating modes of the SPU and its main units, it is possible to select the values of the input and operating parameters that ensure the optimal mode of its operation. In this case, the optimal mode of operation of the SPU is considered to be that which allows obtaining the maximum volume of sulfur with the best quality indicators while observing the technological regulations of the facility and the imposed restrictions.

In this study, the following methods are used to collect and analyze experimental data on the operating modes of the Atyrau Oil Refinery SOB and the initial available fuzzy information:

• Methods of passive and active experiment and mathematical statistics for collecting and processing statistical data on the state and operating modes of SPU units^32,33,34;

• Experimental-statistical methods for constructing models^35,36,37;

• Methods of expert assessments^32,33,34and mathematical tools of fuzzy set theories^38,39,40 for collecting⁴¹ and processing fuzzy information based on a systems approach⁴².

The experimental data on the operating modes of the SOB at the Atyrau refinery were analyzed using regression analysis methods and mathematical statistics techniques. The obtained analysis and processing results of the experimental data from the Atyrau refinery, based on passive and active experiments, were used in the development of statistical models that determine the production volumes of the main SOB units. For passive experiments, statistical data on input, operating, and output parameters were recorded by the process operator (DM) every two hours in operational logs under normal SOB operating conditions. For active experiments, which provide reliable data under various, including extreme, operating conditions, data were obtained by implementing a pre-designed experimental plan based on the mathematical experiment planning method.

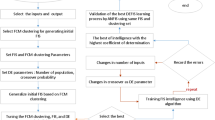
Next, we provide a description of the proposed concept for developing a package of models of technological system units based on a systems approach. The main stages of the proposed concept for developing a package of models based on available information of various types are:

• (1) Determining the purpose of modeling, since various problems can be solved by modeling, for example, predicting the operation of an object, optimizing its parameters, control, etc. And depending on the purpose, the requirements for the models being developed can also be different.

• (2) System analysis of the operation of technological system units and determination of connections and the mutual influence of their parameters, collection and processing of available information of various nature, including fuzzy information necessary for the development of models in accordance with the goal.

• (3) Determination of criteria for selecting the most effective type of developed models for each unit of the technological system, taking into account the set goal. Here, in addition to the standard criteria: accessibility, efficiency of obtaining the necessary information for developing a certain type of model; required level of adequacy; development costs ; suitability for optimization, etc., it is recommended to include in the criteria the ease of combining the type of models being developed into a single package of models.

• (4) Organization and conduct of expert assessment according to the compiled criteria for ranking models developed for each unit of the technological system. Then, based on the value of the integrated criterion, select the most effective type of model for each unit of the technological system. For convenience, the results of the expert assessment are generally recommended to be presented in the form of the following Table 1 (in accordance with stage 4 of the proposed concept).

  Moreover, this stage of the concept includes the following substages:

  • 4.1 If, according to the value of the integrated criterion for a specific aggregate, a deterministic model is effective (gains the maximum rank, i.e., score), then a deterministic model is developed for this aggregate based on theoretical information and other data. Such a model can be developed based on analytical methods. Then the adequacy of the model is checked at stage 11, if the condition for the development of deterministic models is not met, then proceed to the next substage.

  • 4.2 If statistical data is available for the aggregate under consideration and according to the value of the integrated criterion, statistical models gain the maximum score, then statistical models are developed for this aggregate based on experimental statistical methods. Then the adequacy of the developed model is checked at stage 11. If it is impossible to develop statistical models for the aggregate in question, proceed to the next substep.

  • 4.3 The condition for the effectiveness of fuzzy linguistic models is checked. If, according to the value of the integrated criterion, fuzzy linguistic models have the maximum value, then based on a systems approach, expert assessment methods and fuzzy set theories, these models are developed for the selected aggregate. Moreover, if both the input and output parameters of the unit are fuzzy, then its linguistic models are synthesized at stages 6–8. A With clear input and fuzzy output parameters, to develop a fuzzy model of this unit, go to stage 5.

  • 4.4 If theoretical, statistical and fuzzy information for developing an aggregate model is not enough and according to the value of the integrated criterion, hybrid models have the maximum score, then using the available information of various types, hybrid models are developed based on the hybrid method.

• (5) With clear ${x}_{i}\in X,\hspace{0.33em}i=\overline{1,n,}$ inputs and fuzzy outputs ${\widetilde{y}}_{j}\in {\widetilde{B}}_{j},\hspace{0.33em}j=\overline{1,m,}$ where ${\widetilde{A}}_{i}\in X,$ the parameters of aggregates, the structures of fuzzy models are identified in the form of multiple regression equations ${\widetilde{y}}_{j}={f}_{j}\left({x}_{1},\dots ,{x}_{n}, {\widetilde{a}}_{0},{\widetilde{a}}_{1},\dots ,{\widetilde{a}}_{n}\right),\hspace{0.33em}j=\overline{1,m}$. To do this, we can apply the idea of the approach of sequential inclusion of regressors⁴³. Identification of the value of fuzzy parameters (regression coefficients) ${\widetilde{a}}_{0},{\widetilde{a}}_{1},...,{\widetilde{a}}_{n}$ of models ${\widetilde{y}}_{j},$ can be produced based on set level αand modified least square method⁴⁴. Then the transition to stage 11 is carried out to check the adequacy of the resulting model. Otherwise, i.e. in the case of vagueness and input, operating parameters ${\widetilde{x}}_{i}\in {\widetilde{A}}_{i},\hspace{0.33em}i=\overline{1,n}$ move on to the next point.

• (6) Based on the methods of expert assessments using DM , the object is described and the term set of fuzzy parameters is determined $T({X}_{i},{Y}_{j})$ and their membership functions ${\mu }_{{\widetilde{A}}_{i}}\left({\widetilde{x}}_{i}\right)$, are constructed ${\mu }_{{\widetilde{B}}_{j}}\left({\widetilde{y}}_{j}\right).$The following adaptable formula is recommended for constructing the accessory function, for example, output parameters:

  $$\mu_{{B_{j} }}^{t} \left( {\tilde{y}_{j} } \right) = exp\left( {Q_{{\tilde{B}_{j} }}^{t} \left| {\left( {y_{j} - y_{j}^{md} } \right)^{{N_{{\tilde{B}_{j} }}^{t} }} } \right|} \right),$$

  (1)

  where t – term number;${Q}_{{\widetilde{B}}_{j}}^{t}$ – coefficients identifiable at the set level α = 0.5 degree and allowing you to quickly adapt dependence (1) to the graph of the membership function; ${N}_{{\widetilde{B}}_{j}}^{t}$– coefficient that allows you to slowly but more accurately approximate the graph of the membership function ; ${y}_{j}^{md}$– a variable that more accurately corresponds to the selected term is determined from the condition: ${\mu }_{{\widetilde{B}}_{j}}\left({\widetilde{y}}_{j}\right)=\underset{j}{\text{max}}{\mu }_{{\widetilde{B}}_{j}}^{t}\left(\widetilde{{y}_{j}}\right).$ In this case, the process of constructing the membership function can be accelerated if it is possible to select a suitable type of function from the standard functions of the Fuzzy Logic Toolbox application of the MATLAB system, for example, a Gaussian type function (gaussmf) .

• (7) Fuzzy mappings are formalized ${\widetilde{R}}_{ij},$ to determine the connections between $\tilde{x}_{i}$ and ${\widetilde{y}}_{j},$ which are linguistic variables characterized by the input and output parameters of the unit .

• (8) Based on the rule of compositional inference, fuzzy sets are defined, characterized by fuzzy output parameters ${\widetilde{B}}_{j}={\widetilde{A}}_{i}^\circ {\widetilde{R}}_{ij},$ where ${\widetilde{A}}_{i}$−are fuzzy sets that describe the fuzzy input parameters of the unit. For ease of definition ${\widetilde{B}}_{j}$ on a computer, you can formalize them using the accessory function:

  $$\mu _{{B_{j} }}^{t} \left( {\tilde{y}_{j}^{*} } \right) = \mathop {\max }\limits_{{x_{i} \in X}} \left\{ {{\text{min}}\left[ {\mu _{{A_{i} }}^{t} \left( {\tilde{x}_{i}^{*} } \right),\mu _{{\tilde{R}_{{ij}} }}^{t} \left( {\tilde{x}_{j}^{*} ,\tilde{y}_{j} } \right)} \right]} \right\}$$

  (2)

  In expression (2):${\mu }_{{B}_{j}}^{t}\left({\widetilde{y}}_{j}^{*}\right)$ – membership function of fuzzy output parameters described by terms t Then, clear values of the output parameters of the unit from the fuzzy set of their values ${y}_{j}^{**}$ can be determined based on (2) using the formula: ${y}_{j}^{**}=\text{arg}\underset{{\widetilde{y}}_{j}^{*}}{\text{max}}{\mu }_{{B}_{j}}^{*}\left({\widetilde{y}}_{j}^{*}\right).$ The structure of linguistic models is formalized on the basis of fuzzy rules of conditional inference in the form:

  $$IF \tilde{x}_{1} \in \tilde{A}_{1} and \tilde{x}_{2} \in \tilde{A}_{2} and \ldots and \tilde{x}_{n} \in \tilde{A}_{m} , THEN \tilde{y}_{1} \in \tilde{B}_{1} , and \tilde{y}_{2} \in \tilde{B}_{2} and \ldots and \tilde{y}_{m} \in \tilde{B}_{m} ,$$

  (3)

  where ${\widetilde{x}}_{i},i=\stackrel{-}{1,n},$ ${\widetilde{y}}_{j},j=\stackrel{-}{1,m}$ −the linguistic variables discussed above, which describe the fuzzy input and output parameters of units;${\widetilde{A}}_{i},i=\stackrel{-}{1,n}$ and ${\widetilde{B}}_{j},j=\stackrel{-}{1,m}$ −fuzzy sets in which they are defined accordingly ${\widetilde{x}}_{i},i=\stackrel{-}{1,n},$ ${\widetilde{y}}_{j},j=\stackrel{-}{1,m}.$

• (9) Checking the condition of model adequacy, for example, according to the criteria $R=\underset{i}{\text{min}}{\left({y}_{j}^{m}-{y}_{j}^{E}\right)}^{2}\le {R}_{D},$ where $R$ And ${R}_{D}$ – the value of the adequacy assessment criterion and the permissible deviation − is a small value, for example 0.005, determined, for example, depending on the purpose of the modeling or according to the table; ${y}^{M}$ And ${y}^{E}$- the values of the output parameters obtained from the model ( ${y}^{M}$) and from the results of experiments ( ${y}^{E}$), in the case of fuzzy linguistic models, they are determined by defuzzifying their fuzzy values. It is clear that the values of ${y}^{M}$ and ${y}^{E}$ must be obtained with the same values of the input parameters. If the condition is met $R=\underset{i}{\text{min}}{\left({y}_{j}^{m}-{y}_{j}^{E}\right)}^{2}\le {R}_{D}$, the developed models are considered adequate and are recommended for use in practice to solve the problem.

If this condition is not met, then the reasons for the inadequacy of the model are determined and, starting from the previous stages of the concept described, they are eliminated and the next iteration to ensure the adequacy of the developed models is repeated until adequacy is achieved. Further in the next section we develop models of the SOB reactor package based on the concept proposed above

Table 1 A general form for formatting the results of an expert assessment of the effectiveness of various models that are being developed for the main units of the technological system.

Results

The main units of the SPU that affect its operating modes and the processes of sulfur production include: Claus reactors and CBA R ; capacitors E; oven F and pump SOB. We develop their models based on available fuzzy and other data using the concept of developing a package of models of technological system units proposed in the previous section.

System analysis and expert assessment of various types of models developed for the main units of the SPU

Table 2 below contains the results of an expert assessment of various types of models that can be developed for the above main units SOB, according to which the most effective type of model developed for these units is selected.

Table 2 Results of system analysis and expert assessment of the types of models developed for the main units of a sulfur obtaining block.

The results of systematic analysis and expert evaluation of the main units of the sulfur production block at the Atyrau refinery, along with the types of models that can be developed for its individual units, indicate the following (see Table 1):

• Due to the complexity and difficulty of studying the ongoing processes and obtaining the necessary information, the development of deterministic, fuzzy, or hybrid models for determining product volumes from the reactors is practically challenging or economically unfeasible. Based on the maximum value of the integrated criterion, it is evident that for reactors, the most effective type of model for determining product volumes at their outputs is a statistical model, developed using experimental-statistical data. These statistical models are built using available statistical data from passive experiments recorded in the SOB operational logs and additional active experiments conducted specifically for this study⁴⁵.

• Based on the study results, it can be concluded that due to the uncertainty in the practically available data, the fuzzy assessment of sulfur quality parameters at the CBA reactor output necessitates the synthesis of fuzzy models.

• The systematic analysis and expert evaluation presented in Table 2 indicate that, given the availability of initial statistical data and the relative ease of collecting additional experimental-statistical data for the SOB condensers, the most effective model type for these units is also a statistical model.

We present the results of the development of selected effective models based on expert assessment (Table 2) for the F-001 − thermoreactor (TR), R-001 − Claus reactor (RC) and parallel connected reactors CBA R-002 (RCBA-2), R-003 (RCBA-2) SOB.

Models of thermal reactor, Claus, CBA reactors and condensers

Statistical models of the thermoreactor, Claus reactors and CBA are developed using available statistical experimental data obtained on the basis of active experiments. As a result of processing the collected experimental and statistical data, using the idea of ​​the method of sequential inclusion of regressors based on the concept of developing a package of object models proposed in Section "Materials and methods", the structures of the models that determine the volumes of semi-finished products and products from the output of TR, RC and RCBA are identified. The structure of these models is identified in the form of the following system of multiple nonlinear regression Eqs. (4) –(5):

$$y_{TR} = a_{0} + \mathop \sum \limits_{i = 1}^{4} a_{i} x_{i} + \mathop \sum \limits_{i = 1}^{4} \mathop \sum \limits_{k = 1}^{4} a_{ik} x_{i} x_{k} ,$$

(4)

$$y_{RC, RCBA} = a_{0} + \mathop \sum \limits_{i = 5}^{7} a_{i} x_{i} + \mathop \sum \limits_{i = 5}^{7} \mathop \sum \limits_{k = i}^{7} a_{ik} x_{i} x_{k} ,$$

(5)

where ${y}_{TR}$ is the volume of liquid sulfur from the thermoreactor (semi-finished product); ${y}_{RC,CBA}$– the volume of liquid sulfur at the output of Claus reactors, CBA and the quality indicators of the sulfur obtained from them; input, operating parameters of reactors affecting sulfur production processes for a thermoreactor: ${x}_{1}$– volume of raw materials in the thermoreactor; ${x}_{2} \text{and} {x}_{3}$– temperature and pressure of the raw material in TR; ${x}_{4}$ – combustion air consumption at the thermoreactor TR; for Claus and CBA reactors: ${x}_{5}$– volume of raw materials; ${x}_{6}$– temperature in reactors; ${x}_{7}$– pressure in reactors.

Fuzzy models that determine the fuzzily assessed key quality indicators of the produced sulfur at the CBA reactor output (sulfur and water content in sulfur) have been synthesized based on fuzzy information, which represents the experience, knowledge, and judgments of the decision-maker (DM) and expert specialists, expressed in natural language. The collection and processing of such fuzzy expert information was carried out using expert evaluation methods and fuzzy set theory, in accordance with Step 5 of the proposed concept presented in the previous section on the development of a complex system model package. The structure of the fuzzy sulfur quality assessment models, based on a modified idea of the sequential inclusion of regressors method, has been identified in the form of the following system of equations for multiple nonlinear fuzzy regression:

$$\tilde{y}_{RCBA}^{s} = \tilde{a}_{0} + \mathop \sum \limits_{i = 5}^{7} \tilde{a}_{i} x_{i} + \mathop \sum \limits_{i = 5}^{7} \mathop \sum \limits_{k = i}^{7} \tilde{a}_{ik} x_{i} x_{k} ,$$

(6)

$$\tilde{y}_{RCBA}^{W} = \tilde{a}_{0} + \mathop \sum \limits_{i = 5}^{7} \tilde{a}_{i} x_{i} + \mathop \sum \limits_{i = 5}^{7} \mathop \sum \limits_{k = i}^{7} \tilde{a}_{ik} x_{i} x_{k} ,$$

(7)

where ${\widetilde{y}}_{RCBA}^{s}$ – unclear value of the mass fraction of sulfur from the output of the CBA reactors (depending on the type, at least from $\widetilde{97}$ to $\widetilde{98}$%); ${\widetilde{y}}_{RCBA}^{W}$ – fuzzy value of the mass fraction of water from the output of the CBA reactors (no more than from $\widetilde{0.3}$ to $\widetilde{0.9}$%), where $\widetilde{(\cdot )}$ − the tilde sign, hereinafter, means that the corresponding parameters are unclear; input, operating parameters of reactors affecting sulfur production processes for CBA reactors: ${x}_{5}$– volume of raw materials; ${x}_{6}$– temperature of the raw material at the reactor inlet; ${x}_{7}$– pressure in reactors; ${a}_{0l},{a}_{i},{a}_{ik},l=1.2, i=\stackrel{-}{\text{1,4}},k=i, \text{and} {\widetilde{a}}_{0l},{\widetilde{a}}_{i},{\widetilde{a}}_{ik},l=\text{3,4}, i=\stackrel{-}{\text{5,7}},k=i$ – unknown clear and fuzzy parameters (regression coefficients) to be identified, respectively: free term (${a}_{0l}, {\widetilde{a}}_{0l}$); taking into account linear influences (${x}_{i}$), square and mutual influences (${x}_{ik}$), on the volume of liquid sulfur and on its qualities.

Thus, models that determine the yield of sulfur have the form of multiple nonlinear regression, identified by experimental and statistical methods, and models that evaluate the quality of sulfur have the form of fuzzy multiple regression equations and are obtained on the basis of fuzzy information from DM, specialist experts.

Unknown parameters of models (4)–(5) were identified using modified least squares methods using the REGRESS software package⁴⁶. Results of parametric identification of models that determine the dependence of the volume of sulfur from the output of the thermoreactor TR, Claus reactor RC and reactors RCBA (R-002, R-003):

$$\begin{aligned} y_{TR} = & 0.68679x_{1} + 0.0125x_{2} - 0.05200x_{3} - 0.02600x_{4} + 0.02592x_{1}^{2} + 0.00001x_{2}^{2} - 0.00021x_{3}^{2} \\ \quad & - 0.00005x_{4}^{2} + 0.00047x_{1} x_{2} - 0.00059x_{1} x_{4} + 0.0000250x_{2} x_{4} - 0.000104x_{3} x_{4} , \\ \end{aligned}$$

(8)

$$\begin{aligned} y_{RC} = & 0.67123x_{5} + 0.01714x_{6} - 0.01292x_{7} + 0.0788140x_{5}^{2} + 0.00006x_{6}^{2} - 0.00003x_{7}^{2} \\ \quad & - 0.00157x_{5} x_{6} - 0.00059x_{5} x_{7} + 0.00004x_{6} x_{7} \\ \end{aligned}$$

(9)

$$\begin{aligned} y_{RCBA} = & 2.600 + 0.098859316x_{5} + 0.013928571x_{6} + 4.875000000x_{7} + 0.000033163x_{6}^{2} \\ \quad & + 4.062500x_{7}^{2} + 0.123574144x_{5} x_{7} + 0.00004x_{6} x_{7} \\ \end{aligned}$$

(10)

As seen from the results of systematic analysis and expert evaluation, conducted in accordance with the proposed concept for developing a model package (Table 2), the most effective type of models for the heat exchangers E-002 and E-004 of the SOB are deterministic models based on theoretical data. As a result of various theoretical studies, the heating process models proposed in^47,48 were selected and adapted for the SOB heat exchangers. The obtained deterministic models of the SOB heat exchangers (condensers) were integrated into the SOB model package for simulating and optimizing its operating modes.

To construct the SOB condenser models, the following notations are introduced:: ${G}_{1}^{0}$ − Volume of the heated flow (intermediate product); ${T}_{11}^{0}, {T}_{12}^{0}$ − temperatures of the heated flow at the inlet and outlet; ${T}_{21}^{0}, {T}_{22}^{0}$ − temperatures of the heating flow at the inlet and outlet. Thus, the volume of the heated flow at the condenser outlet ${G}_{2}^{0}$, can be determined based on the heat balance condition as follows:

$$G_{2}^{0} = \left( {{\raise0.7ex\hbox{${(T_{11}^{0} - T_{12}^{0} )}$} \!\mathord{\left/ {\vphantom {{(T_{11}^{0} - T_{12}^{0} )} {\left( {T_{21}^{0} - T_{22}^{0} } \right)}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\left( {T_{21}^{0} - T_{22}^{0} } \right)}$}}} \right)G_{1}^{0} .$$

To account for the dynamics of the condenser operation, the mathematical models must be formulated as the following system of differential equations, describing the temperature changes of the heat carrier as it moves through the condenser.

$$\left\{ {\begin{array}{*{20}l} {\frac{{{\text{d}}T_{1} }}{{{\text{d}}z}} = \frac{{T_{2} - T_{1} }}{{c_{1} RG_{1} }}} \hfill \\ {\frac{{{\text{d}}T_{2} }}{{{\text{d}}z}} = \frac{{T_{2} - T_{1} }}{{c_{2} RG_{2} }}} \hfill \\ \end{array} .} \right.$$

(11)

In the given system of differential Eqs. (11): ${T}_{1}$ − temperature of the heat carrier flow in the first circuit; ${T}_{2}$ − temperature of the heat carrier flow in the second circuit; $z$ − relative distance traveled by the heat carrier inside the heat exchanger; ${{c}_{1},c}_{2}$ − heat capacities; R − Average thermal resistance of the partition between the heat carriers. In this system of equations, all parameters except RRR are determined on-site through measurement or reference data.

The above initial data are sufficient to provide the initial conditions for the given differential equations, including:${G}_{1}^{0},{T}_{11}^{0}, {T}_{12}^{0}{T}_{21}^{0}, {T}_{22}^{0}$ for initializing the conditions R − average thermal resistance of the partition R. The proposed model will be sufficiently accurate for the SOB heat exchangers (condensers). This is because, in this case, the thermal resistance remains constant along the length of the tube and corresponds to the average value, while for sufficiently long tubes, edge effects can be neglected.

Thus, the solution to the system of differential equations modeling the heat exchangers will have the following form:

$$\left\{ {\begin{array}{*{20}l} {T_{1} \left( z \right) = T_{m} + \left( {T_{11} - T_{21} } \right)c_{2} G_{2} R_{m} e^{{\frac{1}{R}\left( {\frac{1 - z}{{c_{1} G_{1} }} + \frac{z}{{c_{2} G_{2} }}} \right)}} } \hfill \\ {T_{2 } \left( z \right) = T_{m} + \left( {T_{11} - T_{21} } \right)c_{1} G_{1} R_{m} e^{{\frac{1}{R}\left( {\frac{1 - z}{{c_{1} G_{1} }} + \frac{z}{{c_{2} G_{2} }}} \right)}} } \hfill \\ \end{array} .} \right.$$

(12)

In the obtained heat exchanger model (12): m = 1,2 − input and output parameters of the heat exchangers and their corresponding thermal resistance numbers,

$$\begin{aligned} T_{m} = & R_{m} \left( {e^{{\frac{1}{{c_{2} G_{2}^{0} R}} }} c_{1} G_{1}^{0} T_{11}^{0} - e^{{\frac{1}{{c_{1} G_{1}^{0} R}} }} c_{2} G_{2}^{0} T_{21}^{0} } \right), \\ R_{m} = & \left( {e^{{\frac{1}{{c_{2} G_{2}^{0} R}} }} c_{1} G_{1}^{0} - e^{{\frac{1}{{c_{1} G_{1}^{0} R}} }} c_{2} G_{2}^{0} } \right). \\ \end{aligned}$$

From the equation $T_{1} \left( 1 \right) = T_{12}^{0}$ the average thermal resistance can be determined as follows:

$$R = \frac{{(T_{11}^{0} - T_{12}^{0} ) - (T_{22}^{0} - T_{21}^{0} )}}{{c_{1} G_{1}^{0} (T_{11}^{0} - T_{12}^{0} ){\text{ln}}\left( {\frac{{T_{11}^{0} - T_{12}^{0} }}{{T_{22}^{0} - T_{21}^{0} }}} \right) }}.$$

Thus, based on the developed mathematical models of the heat exchangers (condensers) of SOB, we can determine the values of their key output parameters (product temperatures at the outlet) as follows:

$$T_{12} = T_{1} \left( 1 \right); T_{22} = T_{2} \left( 1 \right),$$

(13)

where ${T}_{12}, {T}_{22}$ –temperature of the product and the heating flow, i.e. the coolant at the outlet of the heat exchangers.

Figure 2 shows a graph of the dependence of the volume of the sulfur semi-product at the output of the TR (F-001) thermoreactor on its temperature.

Fig. 2

Dependency graph ${y}_{TR}={f}_{1}\left({x}_{2}\right), {x}_{1}, {x}_{3}, {x}_{4}$–fixed.

Table 3 presents the simulation results of the Claus reactor using the developed models based on the proposed model package development concept for technological system units, as described in "Materials and methods" section. This concept is based on a systematic approach and is compared with known models proposed in reference⁴³.

Table 3 Simulation results using the developed models based on the model package development concept for technological system units, following a systematic approach, and known models.

The graphical dependence of the volume of high-quality sulfur ${(y}_{RCBA})$ from the output of parallel-connected CBA reactors (RCBA-2, RCBA-3) on their temperature $({x}_{6})$ is presented at fixed values of raw material volume and pressure in the CBA reactors (${x}_{5},{x}_{7}$). From the graphical dependence, it can be concluded that the optimal temperature for the CBA reactors is 280 °C, which ensures the maximum volume of high-quality sulfur (26 tons/day) at nominal fixed values of the remaining input and operating parameters of the reactors. To increase the number of validation points for the model while simultaneously varying all input and operating parameters, the developed CBA reactor model (10) is used. This model allows for the determination of the volume of high-quality sulfur based on the input and operating parameters of the reactors. Figure 3 presents the graphical dependence of the volume of high-quality sulfur ${(y}_{RCBA})$ from the output of parallel-connected CBA reactors (RCBA-2, RCBA-3) on their temperature $({x}_{6})$ at fixed values of the raw material volume and pressure in the CBA reactors (${x}_{5},{x}_{7}$). From this graphical dependence, it can be concluded that the optimal temperature for the CBA reactors is 280 °C, which ensures the maximum volume of high-quality sulfur (26 tons/day) at nominal fixed values of the remaining input and operating parameters of the reactors. To determine the volume of high-quality sulfur while simultaneously varying the input and operating parameters across multiple points, the developed CBA (10) reactor model is used. This model enables the prediction of high-quality sulfur output under varying operating conditions.

Fig. 3

Dependency graph ${y}_{RCBA}=f\left({x}_{6}\right), {x}_{5}, {x}_{7}$–fixed.

To identify the unknown fuzzy parameters of models (6), (7): ${\widetilde{a}}_{0l},{\widetilde{a}}_{i},{\widetilde{a}}_{ik},l=3.4, i=\stackrel{-}{\text{5,7}},k=i$ to assess the quality of sulfur from the output of the Claus reactor, the values of the membership function are taken, constructed according to formula (1) fuzzyly describing the quality of sulfur, on level sets ${\alpha }_{q}=\left(0.5; 0.8; 1\right).$ In this case, i.e. level set b e det since ${\alpha }_{q}=\left(0.5; 0.8; 1;0.8;0.5\right),$ the constructed membership functions according to formula (1) are symmetric, where $0.5; 0.8 -$ the levels of the left side of the function, 1 − is the maximum value, and $0.8;0.5$ − levels of their right side. For each level of ${\alpha }_{q},$ models of fuzzy sulfur quality indicators (6) –(7), can be represented as a system of multiple regression equations, then the problems of parametric identification of their clear coefficients ${{a}_{i}}^{{\alpha }_{q}}, i=\stackrel{-}{\text{5,7}}, q=\stackrel{-}{\text{1,3}}$ can be solved by well-known methods for solving parametric identification problems, for example, the least squares method.

We used the above-mentioned software package REGRESS, which implements the modified least squares method. The obtained clear values of the coefficients of ${{a}_{i}}^{{\alpha }_{q}}, i=\stackrel{-}{\text{5,7}}, q=\stackrel{-}{\text{1,3}}$ fuzzy models (6), (7) are then combined using the following expression of fuzzy set theories:

$$\tilde{a}_{i} = \mathop \cup \limits_{{\alpha \int {\left[ {0.5, 0.8, 1} \right]} }} a_{i}^{{\alpha_{q} }} \;or\;\mu_{{\tilde{A}_{i} }} \left( {\tilde{a}_{i} } \right) = SUP\mathop {\min }\limits_{{\alpha \int {\left[ {0.5,1} \right]} }} \left\{ {\alpha ,\mu_{{\tilde{A}_{i} }} \left( {\tilde{a}_{i} } \right)} \right\}, where a_{i}^{{\alpha_{q} }} = \left\{ {a_{i} |\mu_{{\tilde{A}_{i} }} \left( {\tilde{a}_{i} } \right) \ge \alpha } \right\}.$$

(14)

Thus, models describing the fuzzy dependence of the qualitative indicators of sulfur at the output of the reactors CBA, for example, the mass fraction of sulfur ${\widetilde{y}}_{s}$ on its input, operating parameters (${x}_{5}$ −inlet temperature (200 − 290, ^oC);${x}_{6}$ – combustion air flow (200 − 700 nm/m³); ${x}_{7}$– reactor temperature RCBA (280 − 300, ^oC) have the form;

$$\begin{aligned} \tilde{y}_{s} = & \left( {\frac{0.5}{{0.037008}} + \frac{0.8}{{0.037019}} + \frac{1}{0.037034} + \frac{0.8}{{0.037045}} + \frac{0.5}{{0.037058}}} \right)x_{5} \\ \quad & + \left( {\frac{0.5}{{0.076884}} + \frac{0.8}{{0.76900}} + \frac{1}{0.076917} + \frac{0.8}{{0.076920}} + \frac{0.5}{{0.076940}}} \right)x_{6} \\ \quad & - \left( {\frac{0.5}{{0.169435}} + \frac{0.8}{{0.169458}} + \frac{1}{0.169477} + \frac{0.8}{{0.169495}} + \frac{0.5}{{0.169520}}} \right)x_{7} \\ \quad & + \left( {\frac{0.5}{{0.000010}} + \frac{0.8}{{0.000020}} + \frac{1}{0.000025} + \frac{0.8}{{0.000035}} + \frac{0.5}{{0.000043}}} \right)x_{5}^{2} \\ \quad & + \left( {\frac{0.5}{{0.000092}} + \frac{0.8}{{0.000110}} + \frac{1}{0.000120} + \frac{0.8}{{0.000229}} + \frac{0.5}{{0.000140}}} \right)x_{6}^{2} \\ \quad & - \left( {\frac{0.5}{{0.000007}} + \frac{0.8}{{0.000060}} + \frac{1}{0.000577} + \frac{0.8}{{0.000584}} + \frac{0.5}{{0.000610}}} \right)x_{7}^{2} \\ \quad & + \left( {\frac{0.5}{{0.000050}} + \frac{0.8}{{0.000070}} + \frac{1}{0.000080} + \frac{0.8}{{0.000090}} + \frac{0.5}{{0.000100}}} \right)x_{5} x_{6} \\ \quad & - \left( {\frac{0.5}{{0.000045}} + \frac{0.8}{{0.000065}} + \frac{1}{0.000075} + \frac{0.8}{{0.000085}} + \frac{0.5}{{0.000105}}} \right)x_{5} x_{7} \\ \quad & - \left( {\frac{0.5}{{0.000173}} + \frac{0.8}{{0.000110}} + \frac{1}{0.000210} + \frac{0.8}{{0.000220}} + \frac{0.5}{{0.000245}}} \right)x_{6} x_{7} \\ \end{aligned}$$

(15)

Then, combining the identified clear values (15) of the fuzzy parameters of the model (6) according to expression (11), we obtain the following model, suitable for computer modeling and determining the values ${\widetilde{y}}_{s}$ depending on the values ${x}_{5}, {x}_{6},{x}_{7}$ in the following form:

$$\begin{aligned} \tilde{y}_{S} = & 0.037035x_{5} + 0.076916x_{6} - 0.169480x_{7} + 0.000025x_{5}^{2} + 0.000122x_{6}^{2} - 0.000578x_{7}^{2} \\ \quad & + 0.000080x_{5} x_{6} - 0.000077x_{5} x_{7} - 0.000215x_{6} x_{7} . \\ \end{aligned}$$

(16)

Similarly, the fuzzy parameters of the model (7) were identified; the following model was obtained, which allows us to determine the values ${\widetilde{y}}_{w}$ −mass fraction of water in sulfur depending on ${x}_{5}, {x}_{6},{x}_{7},$ convenient for computer modeling:

$$\begin{aligned} \tilde{y}_{W} = & 0,180 + 0.0002222x_{5} + 0.000120x_{6} + 0.00040x_{7} \\ \quad & + 0.0000008x_{5}^{2} + 0.0000002x_{6}^{2} + 0.0000007x_{7}^{2} . \\ \end{aligned}$$

(17)

Now we will consider the results of the synthesis of linguistic models (in accordance with stages 6 − 8 of the proposed concept for developing a package of models), which allow us to assess the quality of the produced sulfur. Applying the idea of the method of logical rule of conditional inference and the developed base of rules, the structures of linguistic models used to assess the quality of sulfur from the output of reactors R-002, R-003 in a fuzzy environment are identified. The developed linguistic models make it possible to assess the influence of the mass fractions of sulfur, ash, organic substances and water in the composition of sulfur on the quality of the resulting sulfur from SOB. The structure of these linguistic models is determined by expression (8) and synthesized on the basis of rules of the production model type, taking into account the requirements of sulfur quality standards and consists of the following basic rules:

$$\begin{aligned} & IF~MF_{s} \tilde{ \ge }99.96\% ~and~MF_{a} \tilde{ \le }0.023\% ~and~MF_{{om}} \tilde{ \le }0.015\% ~and~MF_{W} \tilde{ \le }0.23\% ,~THEN~SQ = hh,~ELSE~ \\ & IF~MF_{s} \tilde{ \ge }99.94\% ~and~MF_{a} \tilde{ \le }0.032\% ~and~MF_{{om}} \tilde{ \le }0.033\% ~and~MF_{W} \tilde{ \le }0.25\% ,~THEN~SQ = ab\_av,~ELSE \\ & IF~MF_{s} \tilde{ \ge }99.90\% ~and~MF_{{aZ}} \tilde{ \le }0.06\% ~and~MF_{{om}} \tilde{ \le }0.07\% ~and~MF_{W} \tilde{ \le }0.27\% ,~THEN~SQ = av,~ELSE \\ & IF~MF_{s} \tilde{ \ge }99.50\% ~and~MF_{a} \tilde{ \le }0.22\% ~and~MF_{{om}} \tilde{ \le }0.27\% ~and~MF_{W} \tilde{ \le }0.29\% ,~THEN~SQ = bel\_av,~ELSE \\ & IF~MF_{s} \tilde{ \ge }99.20\% ~and~MF_{a} \tilde{ \le }0.43\% ~and~MF_{{om}} \tilde{ \le }0.50\% ~and~MF_{W} \tilde{ \le }1.32\% ,~THEN~SQ = lw \\ \end{aligned}$$

(18)

In synthesized linguistic models (18): ${MF}_{s}, {MF}_{a},{MF}_{om} \text{and} {MF}_{w}$– mass fractions, respectively, of sulfur; ash; organic substances and water containing sulfur from R-001 reactors. R-003;$\widetilde{\ge }$ and $\widetilde{\le }$ − accordingly, fuzzy restrictions “no more” ; and “no less”; $SQ$−sulfur quality; terms $\text{hh}$– high; $\text{ab}\_\text{av}$− above average; av − average; ${\text{bel}}_{\text{av}}$– below average, lw – low.

In production, the quality of sulfur primarily depends on the mass fraction of sulfur − ${MF}_{s}.$ Depending on the value, ${MF}_{s},$ subject to the requirements for other indicators (${MF}_{a},{MF}_{om}, {MF}_{w})$ sulfur is classified into the following grades; highest grade; 1st grade; 2nd grade; 3rd grade and 4th grade. If ${MF}_{s}\widetilde{\ge }99.96\%$, then the quality of sulfur is assessed as “high”, i.e. sulfur is of the highest grade. In the case where ${MF}_{s}\widetilde{\ge }99.94\%$ the quality of sulfur is “above average” and the − sulfur − is classified as 1st grade.${MF}_{s}\widetilde{\ge }99.90\%,$ “average” and the sulfur refers to 2-grade, and if ${MF}_{s}\widetilde{\ge }99.50\%$, then the quality of the sulfur is − “below average,” i.e., 3-grade sulfur. And when ${MF}_{s}\widetilde{\ge }99.20\%,$ the quality of sulfur is assessed as “low”, and the sulfur belongs to the 4th grade. In practice, if the requirements for the mass fraction of ash, organic substances or water are violated , then ${MF}_{a},{MF}_{om}, {MF}_{w},$ the quality of sulfur is rated one grade lower. In such cases, to assess the quality of sulfur, additional rules are added to the rule base of linguistic models, for example:

$$\ \begin{aligned} & IF~MF_{s} \tilde{ \ge }99.96\% ~and~MF_{a} \tilde{ \le }0.023\% ~and~MF_{{om}} \tilde{ \ge }0.015\% ~and~MF_{W} \tilde{ \ge }0.23\% ,~THEN~SQ = ab\_av,~ELSE~ \\ & IF~MF_{s} \tilde{ \ge }99.94\% ~and~MF_{a} \tilde{ \ge }0.032\% ~and~MF_{{om}} \tilde{ \ge }0.033\% ~and~MF_{W} \tilde{ \le }0.25\% ,~THEN~SQ = av,~ELSE \\ & IF~MF_{s} \tilde{ \ge }99.90\% ~and~MF_{{aZ}} \tilde{ \ge }0.06\% ~and~MF_{{om}} \tilde{ \le }0.07\% ~and~MF_{W} \tilde{ \ge }0.27\% ,~THEN~SQ = bel\_av,~ELSE \\ & IF~MF_{s} \tilde{ \ge }99.50\% ~and~MF_{a} \tilde{ \ge }0.22\% ~and~MF_{{om}} \tilde{ \ge }0.27\% ~and~MF_{W} \tilde{ \ge }0.29\% ,~THEN~SQ = lw~ \\ \end{aligned}$$

The resulting linguistic models, based on a rule base, make it possible to assess the quality and grade of sulfur produced from SOB. The membership functions of fuzzy sulfur quality indicators are constructed in the form of a trapezoidal function based on expert assessment methods. For example, membership functions that vaguely evaluate the quality of sulfur as $hh$(“high quality”), according to the indicators ${MF}_{s},$ ${MF}_{a},{MF}_{om}, {MF}_{w}$:

(19)

where ${\mu }_{{MF}_{s}}\left(x\right), {\mu }_{{MF}_{a}}\left(x\right), {\mu }_{{MF}_{om}}\left(x\right)\text{ and} {\mu }_{{MF}_{w}}\left(x\right)$ are the membership functions, respectively, vaguely describing the mass fractions of sulfur, ash, organic substances and water in the composition of the sulfur obtained from the BPS.

As can be seen from the developed models of SOB reactors, in accordance with the concept for developing a package of models of technological system units proposed in Section "Materials and methods", based on available information of various nature, models were obtained that consist of statistical, fuzzy and linguistic models that determine the volume and quality indicators of sulfur produced from the Atyrau SOB refinery.

A package of reactor models for the sulfur production unit for system modeling and optimization of their operating modes. For system modeling and optimization of operating modes of SOB reactors, it is necessary to combine the developed models of the F-001 thermoreactor and R-001, R-002 and R-003 into a single package of models in accordance with their relationships and the flow of the sulfur production process based on the SOB process flow diagram. The scheme for combining models of SOB reactors is presented in Fig. 4. In the given scheme for combining the developed and used models of the main units of SOB into a single package: MTR F-001 − thermoreactor models; MRC R-001, MRCBA R-002 and MRCBA R-003 − according to the Claus reactor model R-001and reactors CBA models: R-002, R-003. In addition to the listed models of SOB reactors developed above, the circuit also uses models of capacitors E-001 and E-004 (MC E-001, MEH E-004), proposed and adapted for the conditions of the Atyrau SOB refinery in⁴⁹.

Fig. 4

Scheme of combining models of the main DCU units into a single system of models.

From the compiled scheme for combining SOB reactor models into a single package of models, it can be seen that the results of modeling one SOB unit, i.e. the output of its model, is the initial data for the models of other units. Results of modeling the operating modes of the thermoreactor − output MTR F-001 is the input data for the capacitor model MC E-001, its results are the input of MEH E-004. Next, the obtained capacitor modeling results are used as input data for the Claus reactor model MRC (R-001), and the results of its simulation are the input data for the parallel-connected CBA reactors MRCBA-1 (R-002) and MRCBA-2 (R-003).

To automate the process of determining the optimal operating modes of SOB reactors, it is necessary to develop special optimization algorithms that allow decisions to be made on choosing the most effective operating mode based on the models and computers developed above and used.

Modeling the process of obtaining sulfur from the SOB to determine the optimal operating modes of the reactors of this unit

Programs have been compiled that implement the developed models of SOB reactors on a computer, allowing one to determine the optimal operating mode of the SOB. This mode of operation is understood as providing the maximum volume of the target − sulfur product from the output of the SOB with the required quality in the Jupyter environment Notebook (Anaconda 3), a programming language Python. Results of computer simulation to determine the best operating mode for SOB Atyrau UPS reactors refinery based on the models of SOB rectors developed above and their comparison with known results and with real data obtained experimentally from the research object are shown in Table 4.

Table 4 Comparison of the results obtained based on the developed models using available information of various types, known deterministic models⁵⁰, developed models and real data obtained experimentally at the SOB Atyrau refinery.

We present the mathematical formulations for optimizing the operating modes of the SOB reactor based on computer modeling. The optimization of SOB reactor operating modes is performed using the developed models of the main SOB units (8)–(12) and (16)–(18), which are integrated into a unified model package following the designed scheme (Fig. 4). The optimization process is carried out by the SOB process operator (DM) using computer modeling. The optimization criterion (objective function) for maximizing production volume with a given quality is the volume of sulfur produced at the CBA reactors of SOB, calculated using model (10), depending on the values of input and operating parameters. Meanwhile, the sulfur quality assessment models (16)–(18) are used as constraints, ensuring that the desired product quality is maintained. When optimizing for improved sulfur quality, the criteria may include maximizing the sulfur content in the final product or minimizing the ash, organic compounds, and water content in the produced sulfur. In this case, the total sulfur output is considered a constraint, ensuring the required production volume is met. The ranges of input and operating parameters, determined according to the technological regulations of SOB, are also taken into account as constraints in the optimization process. Thus, the development of the mathematical model package for the main SOB units, computer modeling, optimization, and analysis of results by the decision-maker (DM) enable the creation of effective models for optimizing the SOB reactor’s operating modes and making well-founded decisions based on mathematical analysis and computer simulations.

Analyzing the data presented in Table 4, obtained from computational experiments using the developed model package, known deterministic models, and experimental data from the SOB at the Atyrau refinery, the following conclusions can be drawn:

• The computational experiment results obtained using the developed model package align more accurately with the experimentally obtained real data compared to the results from known models, indicating that the developed models are more adequate.

• The fuzzy models for sulfur quality assessment, developed based on the proposed systematic approach, enable the determination of fuzzy quality indicators of the produced sulfur that cannot be identified using known deterministic models.

• As shown in Table 4, the optimal sulfur production process achieved through the developed model package requires 0.2 tons/day less raw material consumption than known methods and reduces heat energy consumption by 0.05 °C. This demonstrates that the developed model package, based on the proposed approach, is more efficient, as it enables better process optimization with lower raw material and energy costs.

All these findings confirm the effectiveness of the proposed approach for model development and optimization of complex technological system operations under uncertainty conditions.

Given in Table 3 shows the results of modeling based on the developed models in a fuzzy environment with sufficiently high accuracy that they coincide with real data obtained experimentally at the SOB of Atyrau refinery and are better than the results of known deterministic models.

The developed package of reactor models and other SOB units, along with its software implementation, enables the simulation of various SOB operating modes and facilitates the identification and selection of the most efficient operating conditions. To achieve this, the SOB process operator (decision-maker) can simulate different operating modes of the main SOB units on a computer and analyze the obtained results. This allows them to determine the optimal operating mode, ensuring maximum sulfur output with the highest quality standards, meeting or exceeding the required specifications.

Discussion

The proposed concept for developing a package of interconnected models for technological system units is based on the idea of a systematic approach. By integrating various modeling methods, it enables the development of models for complex, poorly formalized technological systems under conditions of limited and uncertain input data.

The proposed systematic approach leverages available data of various types to develop deterministic, statistical, fuzzy, and linguistic models of technological units, depending on the nature of the available information. Initially, through system analysis and expert evaluation, the most effective model type is selected for each unit based on the characteristics of the accessible data and predefined model evaluation criteria. Then, considering the sequence of technological processes in the system and its technological framework, the developed unit models are integrated into a unified model package, allowing for a systematic simulation of a complex technological system.

Due to the synergy and emergent effects, the developed system of interconnected models for the main SOB units enables effective and adequate systemic modeling and optimization of operating conditions, justifying the superiority of the synthesized model package over other models.

Furthermore, the developed fuzzy and linguistic models are more informative, accurate, and efficient, as they account for deep, hidden relationships between various input and output parameters by utilizing the knowledge, experience, and intuition of expert specialists. Additionally, these models allow for the determination of non-measurable and poorly formalized indicators of technological objects, which cannot be identified using other types of models.

In practice, the qualitative indicators of the produced sulfur are not measured directly by instruments but are evaluated with human participation (specialists) in laboratory conditions based on their experience and knowledge and are characterized by fuzziness. Therefore, to determine the qualitative indicators of sulfur, fuzzy linguistic models are developed based on the proposed concept and methods of expert assessment and fuzzy set theory. Mathematical models for determining the volumes of liquid sulfur from the thermoreactor and Claus reactors of the sulfur production unit are identified as statistical models in the form of nonlinear regression equations. Thus, the package of models for the reactors of the sulfur production unit is developed based on available statistical and fuzzy information.

The optimization of the operating modes of the SOB reactors based on the developed package and their software implementation is carried out by simulating various operating modes on a computer and selecting the best mode by comparing the obtained results. The practical significance of the research results lies in the possibility of exporting them to similar technological processes in oil refining, petrochemicals, and other industries.

Based on the analysis and discussion of the obtained modeling results and the determination of the optimal operating mode of the reactors using both known and newly developed models presented in Table 4, the following advantages of the proposed systematic approach to developing a model package can be noted:

• The developed package of SOB reactor models, based on the proposed concept and a systematic approach to modeling a complex of interconnected units within a technological system using various available data, is more adequate for real-world objects compared to known models. The modeling results for optimizing the studied object in a fuzzy environment more accurately correspond to the real data obtained experimentally from the SOB at the Atyrau refinery than the results of existing modeling methods.

• The systematic modeling of interconnected SOB reactors and optimization of their operating modes allows for the determination of the most efficient reactor operating conditions. As a result of computer modeling and optimization of SOB reactor operation modes, compared to the results obtained using known modeling and optimization methods, sulfur output has increased by 2 tons per day, or 8% per day. Furthermore, as shown in the comparison results (Table 4), the developed models in a fuzzy environment improve the quality characteristics of the obtained sulfur, which cannot be determined using other known models. Based on the obtained results, the developed fuzzy models allow increasing the sulfur content in the final product by 0.05%, minimizing the ash content to 0.002%, and reducing the organic matter content to 0.016%. Thus, the developed models increase the amount of recovered sulfur while improving its quality characteristics, meaning more high-grade sulfur is produced. This provides a significant economic benefit from selling higher-quality sulfur and significantly improves environmental conditions.

• A crucial task in modeling and optimizing technological production facilities is determining and controlling the quality of the produced product. The developed models, which optimize the operating modes of the studied SOB reactors in a fuzzy environment, allow for the assessment of the quality indicators of the produced sulfur, including the mass fraction of sulfur, ash, organic matter, and water, which cannot be determined using existing methods. These quality indicators are assessed based on the experience, knowledge, and intuition of domain experts and specialists, which is another key advantage of the proposed approach.

The novelty and advantages of the proposed systematic method for modeling complex systems, compared to existing methods, lie in the application of a systemic approach that integrates deterministic, statistical, fuzzy modeling, expert assessments, and fuzzy set theory. The proposed systematic method accounts for uncertain and fuzzy parameters, enhancing the prediction of the performance of complex, poorly formalized technological systems, such as sulfur production blocks.

A key innovation of the study is the application of a combination of formal and informal systemic analysis methods, along with the proposed systematic method for developing a package of effective models for interconnected technological system units. The proposed concept for developing a package of interconnected elements in a complex system introduces new approaches to modeling poorly formalized objects under conditions of limited and fuzzy input data. The newly developed approaches to fuzzy modeling allow for the creation of fuzzy or linguistic models based on corresponding operations and rules of fuzzy set theory, depending on the fuzziness of the input and output parameters of the objects.

The obtained research results provide operational improvements for SPU (Sulfur Production Units) at oil refineries by selecting optimal operating conditions that increase sulfur output with the best quality indicators while minimizing energy consumption. This optimized operation of SPU leads to significant economic benefits through the sale of high-quality sulfur and environmental improvements, as it allows for the more efficient processing of harmful sulfur-containing gases, reducing their environmental impact.

To improve the quality and reliability of the models, an analysis and discussion of error sources in the models were conducted. The main sources of errors in the developed models were identified as follows:

•  Data errors due to the lack of sufficient reliable data on the operating modes of the main SOB units and the stochastic nature of the available data.

• Model errors related to the incorrect selection of the model type and improper identification of model structure and parameters.

• Interpretation errors that may lead to incorrect conclusions.

These errors negatively affect the final modeling results, reducing the quality and reliability of the developed models. The proposed concept for developing a package of interconnected technological system models, based on a systematic approach, includes methods for preventing and eliminating the identified error sources. The proposed systematic approach ensures that the most effective model type for each unit is selected and developed using available data of various types, combining systematic analysis and expert evaluation. These models are then integrated into a unified package. The proposed concept also includes procedures for verifying and ensuring the adequacy of the developed models, while systematic modeling based on the model package allows for the correct interpretation of modeling results.

The main limitations of the proposed approach to modeling and optimizing the operating modes of the research object can be:

• The complexity of assessing the degree of membership and constructing membership functions that fuzzily describe unmeasured parameters and adequately describe them.

• Possible difficulties for the decision maker in the operational optimization of the object’s operating modes, related to the lack of time for modeling various operating modes of the object, comparing the obtained results, and selecting the best mode.

To eliminate these limitations of the proposed systematic approach, the authors plan the following in further research:

• The design and creation of a computer system supporting the process of assessing membership degrees and constructing adequate membership functions that fuzzily describe unmeasured parameters in dialogue with the decision maker and domain experts. Such a computer system significantly accelerates and supports the process of analysis and selection of the best operating mode in the management of the studied object by automating a significant part of these tasks.

• To facilitate the function of the decision maker in the processes of operational optimization of the object’s operating modes by modeling various operating modes and comparing the obtained results to select the best mode, it is necessary to additionally develop and apply decision-making methods. These methods should promptly, taking into account the preferences of the decision maker, select the optimal operating mode and should be functional in a fuzzy environment.

Conclusion

During the research conducted, the following main results were obtained:

• 1. A concept for developing a package of models for interconnected units of a technological system based on a systematic approach has been proposed. This concept is grounded in the use of available information of various natures and allows for the creation of a package of models for complex technological systems characterized by information deficit and fuzziness.

• 2. Systematic analysis and expert evaluation of different types of models developed for the main units of the sulfur production plant were carried out, and the most effective type of model for each unit was determined, developed, and used.

• 3. The most effective models for the thermoreactor, Claus reactors, and CBA of the sulfur production unit have been developed and combined into a unified model package based on the proposed concept of developing a package of models for interconnected units of a technological system.

• 4. Software implementation of the developed models for the thermoreactor, Claus reactors, and CBA was carried out, and computer simulation was conducted to select the optimal operating mode of the SOB. The simulation results based on the developed package of SOB reactor models, known models, and experimental data from the SOB at the Atyrau refinery were compared. The advantages of the developed models over known deterministic models were identified in the discussion section.

The novelty of the obtained results lies in the development of a concept for a package of models for interconnected units of a technological system using available information of various natures based on a systematic approach, allowing for the synthesis of effective models of the units of the studied system. The developed models for the sulfur production unit reactors allow for systematic modeling of the interconnected reactor complex and the determination of their optimal operating modes. The proposed concept for developing a package of effective models for complex systems, based on using available information of various natures, enables the creation of a package of models for complex technological systems characterized by information deficit and fuzziness. The resulting system of reactor models, due to the synergistic effect and emergent properties of the system, ensures the high efficiency of the proposed systematic approach to modeling a system of interconnected units in conditions of information deficit and fuzziness necessary for developing their models.

The reliability of the results, scientific principles, and conclusions obtained in the work is confirmed by the correctness of the research methods used, based on the scientific principles of system analysis and modeling theory, and by the adequacy and good agreement of the obtained results with the experimental and industrial research results.