Introduction

In recent years, organic semiconductors have garnered significant attention in the fields of electronics and photonic devices due to their versatile applications in optoelectronics, space technology, sensor fabrication, solar cells, and memory devices1. These materials are particularly advantageous because their π-electron systems allow them to transition into a conducting state, which is highly dependent on their unique chemical structures1,2. Among these, Acid Magenta stands out as a promising organic semiconductor. Naturally, it exhibits a polycrystalline structure with an anorthic type lattice, making it both environmentally friendly and cost-effective. Additionally, its ease of synthesis and handling enhances its appeal for various applications.

Fuchsine (\(\:{C}_{20}{H}_{19}{N}_{3}HCl\left[m,\:n\right]\)) is a triamine salt with two main amines and a secondary amine. A blend of rosaniline, pararosaniline, new fuchsine, and magenta II makes up basic fuchsine. Acid Magenta (C20H17N3Na2O9S3[m, n]) is a combination of homologues of basic fuchsine that have had sulfonic groups added to them. This modification not only imparts the dye with a distinctive greenish-yellow hue and high metallic luster but also makes it exceptionally soft, comparable to or softer than talc. Acid Magenta is widely used as a histological dye to enhance contrast in microscopic and electron microscopic examinations, helping to visualize specific cellular components, such as nuclei and cytoplasm. Its ability to differentiate cells from surrounding connective tissues further underscores its utility in biological and medical research.

In the context of chemical graph theory, the molecular structure of compounds like Acid Magenta can be represented numerically using topological indices, which capture the underlying topology of a molecule’s graph. These indices are crucial in establishing correlations between molecular structures and their physico-chemical properties, playing an essential role in quantitative structure-activity relationships (QSAR) and quantitative structure-property relationships (QSPR). Among the earliest and most widely studied topological descriptors are the Zagreb indices, originally introduced to estimate the total π-electron energy of molecules. These indices are calculated from the degrees of vertices within the molecular graph, offering insights into the electronic structure and reactivity of the compounds. It was demonstrated that the total π-electron energy \(\:\left(E\right)\) of a molecule \(\:M\) depends on the quantity \(\:\:\sum\:_{y\in\:V\left(G\right)}{\delta\:\left(y\right)}^{2}\) (now a days called the first Zagreb index), where \(\:G\) is the graph of the molecule \(\:M,\:\) \(\:V\left(G\right)\) corresponds to the vertex set of \(\:G\) and \(\:\delta\:\left(y\right)\) corresponds to degree of the vertex \(\:y\) (number of vertices adjacent to a vertex \(\:y\) in a graph \(\:G\) is equal to its degree). In molecular graph theory, chemical structure of a chemical compound /molecule is represented by its molecular graph. The molecular structure descriptor correlates with many physico-chemical characteristics of the concerned chemical compounds. These descriptors of molecular structure are commonly called as topological indices which are numeric parameters derived from molecular graphs that are invariant under automorphism. Thus, topological indices are an important tools for distinguishing isomers, and they have also demonstrated their utility in QSPR and QSAR3, and nanotechnology including drug discovery and design4. In mathematical chemistry, topological indices have various categories; distance-based indices5,6,7,8,9, spectrum-based indices10,11,12,13,14, vertex-degree-based indices15,16,17,18,19,20,21 and connection-based indices22,23,24,25,26.

In 1947, Wiener introduced the concept of a topological index during his studies on the boiling points of paraffins, coining it the Wiener index27. This foundational work laid the groundwork for subsequent research in molecular graph theory. Building on Wiener’s contributions, M. Darafsheh28 developed methods to calculate both the Wiener and Szeged indices across various graph structures. In addition, A. Ayache29 extended these concepts by calculating topological indices specifically for mk-graphs, while Wei Gao et al.30 explored eccentricity-based topological indices within the cycloalkane family. Topological indices that are based on vertex degrees have proven particularly effective for correlating molecular structures with their physico-chemical properties. These indices are essential in establishing quantitative relationships between structure and behavior in chemical compounds. Ullah and Zaman have made significant contributions in this area, conducting extensive research on degree-based topological descriptors for a wide range of molecular structures31,32,33,34,35,36,37,38,39,40,41,42,43,44. For additional insights into the topological characterization of molecular and microstructures, the refs45,46,47,48,49,50,51,52,53,54. offer a comprehensive exploration of this subject.

The 1st Zagreb index55 is the oldest vertex degree based index, defined as:

$$\:{M}_{1}\left(G\right)=\:\sum\:_{y\in\:V\left(G\right)}{\delta\:\left(y\right)}^{2}$$

This index, along with its extensions such as the multiplicative Zagreb indices, exponential Zagreb indices, and other vertex-degree-based descriptors, has been extensively studied for its utility in understanding molecular properties. Notably, these indices are invaluable for distinguishing isomers and optimizing molecular structures for applications in fields such as drug discovery, nanotechnology, and materials science. For detailed understanding of these indices, reader can consult refs56. and citations therein. Though in the literature, many types of Zagreb indices are introduced but the 1st and 2nd multiplicative Zagreb indices57, Zagreb Co-indices58, and59 are most valued. The multiplicative exponential Zagreb indices, the 1st exponential Zagreb index, and 2nd exponential Zagreb index for \(\:{C}_{n}\:,\:\:{K}_{n}\:,\:{P}_{n}\:,\:{S}_{n}\:,\:{W}_{n}\:\)are studied in60. Notations and terminology can be found in refs45,46,61. except if otherwise stated, are not defined here.

Consider G is a molecular graph, \(\:V\left(G\right)\) and \(\:E\left(G\right)\) are vertex and edge sets of a graph \(\:G\). The degree of vertex in any graph G refers to number of edges connected to a given vertex. It is represented by \(\:\delta\:\left(y\right)\).

Gutman and Trinajstić introduced the 1st Zagreb index over 30 years ago55, and is defined as

$$\:{M}_{1}\left(G\right)=\:\sum\:_{y\in\:V\left(G\right)}{\delta\:\left(y\right)}^{2}$$
(1)

The 1st Multiplicative Zagreb Index, presented by Todeschini et al.62, can be defined as

$$\:\:\:{\prod\:}_{1}G=\:\prod\:_{y\in\:V\left(G\right)}{\delta\:\left(y\right)}^{2}$$
(2)

The modified 1st Zagreb index was proposed in63, it is defined as

$$\:{M}_{1}^{*}\left(G\right)=\:\sum\:_{y\in\:V\left(G\right)}\frac{1}{{\delta\:\left(y\right)}^{2}}$$
(3)

The forgotten topological index64 can be defined as

$$\:{F}_{N}\left(G\right)=\:\sum\:_{y\in\:V\left(G\right)}{\delta\:\left(y\right)}^{3}$$
(4)

The inverse degree index65, a vertex based graph invariant is defined as

$$\:ID\left(G\right)=\sum\:_{y\in\:V\left(G\right)}\frac{1}{\delta\:\left(y\right)}$$
(5)

The first exponential Zagreb index60, introduced by Nihat Akgunes and Busra Aydin, is define as

$$\:{EM}_{1}\left(G\right)=\sum\:_{y\in\:V\left(G\right)}{e}^{{\delta\:\left(y\right)}^{2}}$$
(6)

Multiplicative exponential Zagreb index60 can be defined as

$$\:E{\prod\:}_{1}\left(G\right)=\:\prod\:_{y\in\:V\left(G\right)}{e}^{{\delta\:\left(y\right)}^{2}}$$
(7)

This study is driven by the substantial industrial significance and diverse applications of Acid Magenta, particularly in dye manufacturing, histology, and materials science. Our primary objective is to leverage chemical graph theory to model the molecular structure of Acid Magenta using vertex partitioning techniques. By doing so, we aim to compute a series of topological descriptors, including those mentioned above (Eqs. 1–7), and derive closed-form expressions for them. This mathematical representation will provide a deeper understanding of the structural properties of Acid Magenta, enhancing its potential for applications in QSAR/QSPR analysis, thus paving the way for future innovations in the design of organic semiconductors and related materials.

Molecular topological modeling of acid magenta

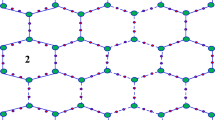
The 2D graph of Acid Magenta molecular structure is given in Fig. 1. We define \(\:m\) as the number of linked unit cells in a row and \(\:n\) as the number of associated rows with each number of \(\:m\) cells. The order of the following molecular graph is \(\:38mn+m+n,\:\)and total number of edges are \(\:42mn\). To abstract the topological indices mentioned in Sect. 1, we have partitioned the total number of vertices in three different sets, say \(\:{V}_{1}\), \(\:{V}_{2}\:,\) and \(\:{V}_{3}\). The set \(\:{V}_{1}\) contains those vertices which have degree\(\:\:1\). Set \(\:{V}_{2}\) contain the vertices with degree two and set \(\:{V}_{3}\) contain the vertices with degree three, respectively. Table 1 shows vertex partition of Acid Magenta’s graph.

Fig. 1
figure 1

Chemical structure of Acid Magenta (a) 3D (b) 2D (c) Graph theoretic model of the chemical structure of Acid Magenta, C20H17N3Na2O9S31.

Full size image
Table 1 Vertex partition of acid magenta.
Full size table

Main results

Derivation of closed formulae for the topological indices of acid magenta

Consider the graph \(\:G\cong\:\:\) C20H17N3Na2O9S3[m, n] of molecular structure of Acid Magenta with \(\:m,\:n\ge\:1,\:\)then;

  1. (1)

    \(M_{1} \left( G \right) = ~220mn - 2m - 2n\)

  1. (2)

    \(\mathop \prod \limits_{1} \left( G \right)~ = ~~~1584mn\left( { - m + 2mn - n} \right)\left( {m + 7mn + n} \right)\)

  1. (3)

    \(M_{1}^{*} \left( G \right) = ~\frac{{305mn}}{{18}} + \frac{{7m}}{4} + \frac{{7n}}{4}\)

  1. (4)

    \(F_{N} \left( G \right) = ~624mn - 6m - 6n\)

  1. (5)

    \(ID\left( G \right) = ~\frac{1}{6}\left( {9n + m\left( {9 + 134n} \right)} \right)\)

  1. (6)

    \(EM_{1} \left( G \right) = 178415.096mn - 49.162m - 49.162n\)

  1. (7)

    \(E\mathop \prod \limits_{1} \left( G \right)~ = 52909000mn\left( {2mn - m - n} \right)\left( {7mn + m + n} \right)\)

Proofs

Consider \(\:G\:\)as graph of Acid Magenta. By the help of Table 1 and Eqs. 1–7 we will compute the following TIs and will derive formulas for them.

  1. (1)

    The first Zagreb index

    By Table 1 and Eq. (1), value of 1st Zagreb index is;

    $$M_{1} \left( G \right) = \sum\limits_{{y \in V\left( G \right)}} {\delta \left( y \right)} ~^{2}$$
    $$\begin{aligned} M_{1} \left( G \right) = & ~\mathop \sum \limits_{{y \in V_{1} \left( G \right)}} \delta \left( y \right)^{2} + ~\mathop \sum \limits_{{y \in V_{2} \left( G \right)}} \delta \left( y \right)^{2} + ~\mathop \sum \limits_{{y \in V_{3} \left( G \right)}} \delta \left( y \right)^{2} \\ ~ = & ~~\left( 1 \right)^{2} \left( {14mn + 2\left( {m + n} \right)} \right) + \left( 2 \right)^{2} \left( {2mn - m - n} \right) + ~\left( 3 \right)^{2} \left( {22mn} \right) \\ ~ = & ~~220mn - 2m - 2n \\ \end{aligned}$$
  2. (2)

    The first multiplicative Zagreb index

    By Table 1 and Eq. (2), the value of 1st multiplicative Zagreb index is;

    $$\:{\prod\:}_{1}\left(G\right)=\:\prod\:_{y\in\:V\left(G\right)}{\delta\:\left(y\right)}^{2}$$
    $$\begin{aligned} \mathop \prod \limits_{1} \left( G \right) = ~ & \mathop \prod \limits_{{y \in V_{3} \left( G \right)}} \delta \left( y \right)^{2} \times ~~\mathop \prod \limits_{{y \in V_{2} \left( G \right)}} \delta \left( y \right)^{2} \times ~\mathop \prod \limits_{{y \in V_{3} \left( G \right)}} \delta \left( y \right)^{2} \\ = & \left( 1 \right)^{2} \left( {14mn + 2\left( {m + n} \right)} \right) \times \left( 2 \right)^{2} \left( {2mn - m - n} \right) \times ~\left( 3 \right)^{2} \left( {22mn} \right) \\ ~ = & ~~1584mn\left( { - m + 2mn - n} \right)\left( {m + 7mn + n} \right) \\ \end{aligned}$$
  3. (3)

    The modified first Zagreb index

    We compute the modified 1st Zagreb index by Table 1 and Eq. (3) as;

    $$\:{M}_{1}^{*}\left(G\right)=\:\sum\:_{y\in\:V\left(G\right)}\frac{1}{{\delta\:\left(y\right)}^{2}}$$
    $$\begin{aligned} M_{1}^{*} \left( G \right) = & ~\mathop \sum \limits_{{y \in V\left( G \right)}} \frac{1}{{\delta \left( y \right)^{2} }} + \mathop \sum \limits_{{y \in V\left( G \right)}} \frac{1}{{\delta \left( y \right)^{2} }} + \mathop \sum \limits_{{y \in V\left( G \right)}} \frac{1}{{\delta \left( y \right)^{2} }} \\ ~ = & \left( {14mn + 2m + 2n} \right) + \frac{1}{4}\left( {2mn - m - n} \right) + \frac{1}{9}\left( {22mn} \right) \\ = & ~\frac{{305mn}}{{18}} + \frac{{7m}}{4} + \frac{{7n}}{4} \\ \end{aligned}$$
  4. (4)

    The forgotten topological index

    The value of forgotten topological index is computed using Table 1 and Eq. (4) as follow

    $$\:{F}_{N}\left(G\right)=\:\sum\:_{y\in\:V\left(G\right)}{\delta\:\left(y\right)}^{3}$$
    $$\begin{aligned} F_{N} \left( G \right) = ~ & \mathop \sum \limits_{{y \in V_{1} \left( G \right)}} \delta \left( y \right)^{3} + ~\mathop \sum \limits_{{y \in V_{2} \left( G \right)}} \delta \left( y \right)^{3} + ~\mathop \sum \limits_{{y \in V_{3} \left( G \right)}} \delta \left( y \right)^{3} \\ ~ = & ~~\left( 1 \right)^{3} \left( {14mn + 2\left( {m + n} \right)} \right) + \left( 2 \right)^{3} \left( {2mn - m - n} \right) + ~\left( 3 \right)^{3} \left( {22mn} \right) \\ ~ = ~ & ~624mn - 6m - 6n \\ \end{aligned}$$
  5. (5)

    The inverse degree index

    We compute the inverse degree index by the help of Table 1 and Eq. (5) as;

    $$\:ID\left(G\right)=\sum\:_{y\in\:V\left(G\right)}\frac{1}{\delta\:\left(y\right)}$$
    $$\begin{aligned} ID\left( G \right) = & \mathop \sum \limits_{{y \in V_{1} \left( G \right)}} \frac{1}{{\delta \left( y \right)}} + \mathop \sum \limits_{{y \in V_{2} \left( G \right)}} \frac{1}{{\delta \left( y \right)}} + \mathop \sum \limits_{{y \in V_{3} \left( G \right)}} \frac{1}{{\delta \left( y \right)}} \\ = & ~\left( {14mn + 2m + 2n} \right) + \frac{1}{2}\left( {2mn - m - n} \right) + \frac{1}{3}\left( {22mn} \right) \\ = & ~\frac{1}{6}\left( {9n + m\left( {9 + 134n} \right)} \right) \\ \end{aligned}$$
  6. (6)

    The first exponential Zagreb index

    We compute 1st exponential Zagreb index using Table 1 and Eq. (6) as;

    $$\:{EM}_{1}\left(G\right)=\sum\:_{y\in\:V\left(G\right)}{e}^{{\delta\:\left(y\right)}^{2}}$$
    $$\begin{aligned} EM_{1} \left( G \right) = & \mathop \sum \limits_{{y \in V_{1} \left( G \right)}} e^{{\delta \left( y \right)^{2} }} + \mathop \sum \limits_{{y \in V_{2} \left( G \right)}} e^{{\delta \left( y \right)^{2} }} + \mathop \sum \limits_{{y \in V_{3} \left( G \right)}} e^{{\delta \left( y \right)^{2} }} \\ ~ = ~ & ~e^{{\left( 1 \right)^{2} }} \left( {14mn + 2m + 2n} \right) + e^{{\left( 2 \right)^{2} }} \left( {2mn - m - n} \right) + e^{{\left( 3 \right)^{2} }} \left( {22mn} \right) \\ ~ = & ~~178415.096mn - 49.162m - 49.162n \\ \end{aligned}$$
  7. (7)

    The multiplicative exponential Zagreb index

    We compute the multiplicative exponential Zagreb index by using Table 1 and Eq. (7) as;

    $$\:E{\prod\:}_{1}\left(G\right)=\:\prod\:_{y\in\:V\left(G\right)}{e}^{{\delta\:\left(y\right)}^{2}}$$
    $$\begin{aligned} E\mathop \prod \limits_{1} \left( G \right)~ = ~ & \mathop \prod \limits_{{y \in V_{1} \left( G \right)}} e^{{\delta \left( y \right)^{2} }} ~ \times ~\mathop \prod \limits_{{y \in V_{2} \left( G \right)}} e^{{\delta \left( y \right)^{2} }} \times ~\mathop \prod \limits_{{y \in V_{3} \left( G \right)}} e^{{\delta \left( y \right)^{2} }} \\ = ~ & ~e^{{\left( 1 \right)^{2} }} \left( {14mn + 2m + 2n} \right) \times e^{{\left( 2 \right)^{2} }} \left( {2mn - m - n} \right) \times e^{{\left( 3 \right)^{2} }} \left( {22mn} \right) \\ = & 52909000mn\left( {2mn - m - n} \right)\left( {7mn + m + n} \right) \\ \end{aligned}$$

Numerical analysis and graphical visualization of computed topological indices

The applications of Degree-based topological indices are extensive across various fields, like pharmaceuticals, chemistry, biomedical sciences, and computer science. These indices provide scientists with valuable numerical and graphical insights into the analyzed data. In this study, we have numerically calculated various degree-based topological indices for Acid Magenta at diverse values of m and n. To facilitate comparison, we also compiled a table (Table 2) that presents these indices for varying m and n values, enabling a straightforward numerical comparison of the molecular structure. As observed in Table 2, the indices consistently increase in value as the parameters m and n grow.

Table 2 Comparison of computed TIs for acid magenta.
Full size table

The graphical representation and comparison of our calculated results for varying values of m, and n in C20H17N3Na2O9S3 [m, n] can be seen in the Figs. 2, 3 and 4. It is evident from the Table 2; Figs. 2, 3 and 4, values of all given indices are increasing as we increase the corresponding values of m, n.

Fig. 2
figure 2

Comparison of 1st Zagreb index and Modified 1st Zagreb index.

Full size image
Fig. 3
figure 3

Comparison of 1st exponential Zagreb index and the forgotten topological index.

Full size image
Fig. 4
figure 4

Comparison of inverse degree index, multiplicative exponential Zagreb index and the 1st multiplicative Zagreb index.

Full size image

Testing the property prediction potential and effectiveness of the considered topological indices in QSPR analysis

Topological indices considered here can be used to predict some physicochemical properties and various substance parameters, including the acentric factor, B.P (boiling point), enthalpy of vaporization and entropy. According to guidelines of ‘The International Academy of Mathematical Chemistry (IAMC)’ to assess the effectiveness of any topological index in modeling physicochemical attributes regression analysis is commonly employed66. Octane isomers are particularly useful due to their structural diversity, which results in branching patterns, non-polar properties and forms. These organic compounds are ideal for statistical testing due their ample number of structural isomers and the availability of comprehensive experimental data for each of them. As noted by Randić and Trinajstić67, linking theoretical invariants to experimentally found physicochemical properties of octane isomers is beneficial for determining the predictive power of an invariant68,69.

In this study, firstly we computed topological indices for eighteen octane isomers and investigated the correlation of the calculated values and experimental parameters to evaluate the predictive potential and practical applicability of these indices. The experimental values were sourced from PubChem, Chemspider databases and study66. The calculation of topological indices for these isomers were carried out by following methods similar to those described in Sect. 3.1.

Through linear fitting, we investigated four physicochemical characteristics of eighteen octane isomers. The analysis and visualization of results were conducted using Origin, MATLAB, and Excel softwares. The correlations of the physicochemical characteristics of octane isomers and their topological indices are illustrated in Figs. 5, 6, 7, 8, 9 and 10. The values of correlation coefficients are presented in Table 3.

It can be seen from Figs. 5, 6, 7, 8, 9 and 10; Table 3 that M1(G), FN(G) and ID(G) have strong correlations with all the four physical properties, M1*(G) has good correlation value for HVAP (Enthalpy of Vaporization) and EM1(G) has good correlation for DHVAP (Standard Enthalpy of Vaporization) and HVAP. It can also be seen that, among all these indices, ID(G) is the best predictor of entropy, Acentric Factor and DHVAP, and M1(G) is the best predictor of HVAP having strongest correlation. However, ∏_1(G) index does not show good correlation to model and predict any property. Here, the weaker associations of some indices with certain properties indicate that they are influenced by factors beyond the scope of these specific topological indices alone, such as intermolecular interactions or external conditions that are not fully encapsulated by concerned indices.

Fig. 5
figure 5

The Correlation of FN(G) with experimental properties of octane isomers.

Full size image
Fig. 6
figure 6

The Correlation of M1(G) with experimental properties of octane isomers.

Full size image
Fig. 7
figure 7

The Correlation of ID(G) with experimental properties of octane isomers.

Full size image
Fig. 8
figure 8

Correlation of EM1(G) with experimental properties of octane isomers.

Full size image
Fig. 9
figure 9

The Correlation of M1*(G) with experimental properties of octane isomers.

Full size image
Fig. 10
figure 10

The Correlation of \(\:{\prod\:}_{1}\left(G\right)\) with experimental properties of octane isomers.

Full size image
Table 3 Values of the correlation coefficients.
Full size table

Conclusion

Molecular descriptors offer crucial insights into the chemical structure of molecules, playing a significant role in analyzing the QSPR (Quantitative Structure–Property Relationships) and QSAR (Quantitative Structure–Activity Relationships). These models are essential for correlating molecular structures or properties with descriptors that can predict chemical and biological activities. In this study, we focused on modeling and topologically characterizing the molecular structure of Acid Magenta using vertex partitioning techniques. We successfully computed and derived various expressions for several key topological indices; the 1st Zagreb index, 1st Multiplicative Zagreb index, Forgotten Topological index, Modified 1st Zagreb index, Inverse Degree index, 1st Exponential Zagreb index, and Multiplicative Exponential Zagreb index. The numerical results obtained from these models, across various values of m and n, demonstrated the effectiveness of all these topological indices to predict the physicochemical properties. To test the predictive potential of the above mentioned indices, we investigated four physicochemical characteristics of all the eighteen octane isomers through linear fitting. The results show that, the indices M1(G), FN(G) and ID(G) have strong correlations with all the four physical properties, M1*(G) has good correlation with HVAP and EM1(G) has good correlation with HVAP and DHVAP. Among all these indices, ID(G) is the best predictor of entropy, Acentric Factor and DHVAP, and M1(G) is the best predictor of HVAP having strongest correlation. These findings underscore the importance of the derived formulas in accurately modeling the molecular structure of Acid Magenta, providing valuable tools for future QSAR/QSPR analysis.