Introduction

Mechanical tunneling remains extensively utilized in mining and civil engineering applications, particularly in light of the rapid development of underground space infrastructure in recent years. However, severe tool wear and low cutting efficiency persist as critical challenges during hard rock excavation. In practice, tunneling efficiency constitutes the primary limiting factor for overall mining productivity. The dominant cutting tools employed in mechanical hard rock excavation include conical picks, chisel picks, and indenters. During the cutting process, these tools engage with the rock mass through continuous linear contact. Specifically, conical and chisel picks fragment rock by generating tensile or shear cracks through tangential scratching with controlled penetration depth. In contrast, indenters operate via normal indentation into the rock surface, initiating localized crushing zones that subsequently propagate to achieve rock fragmentation. As the chisel pick forms tensile cracks using its sharp edge, the application of chisel pick is limited to excavating low-to-medium strength and non-abrasive rocks1. The conical pick features a blunter tip geometry compared to the chisel pick, a design compromise that enhances structural integrity at the expense of requiring substantially higher thrust forces to break rock. The conical pick is composed of the tungsten carbide head and steel support with differential wear rates, where accelerated wear of the steel support frequently leads to tungsten carbide head detachment. Consequently, conical picks have primary application in excavating high-strength, non-abrasive rock formations where structural durability outweighs operational efficiency considerations. In contrast, the rolling disc cutter applied on the tunnel boring machine (TBM) demonstrates distinct performance characteristics. Despite exhibiting lower cutting efficiency relative to chisel/conical picks under equivalent thrust conditions, disc cutters dominate hard rock excavation projects in civil engineering.

Compared with the cutting tools introduced above, the oscillation disc cutter (ODC) is rarely used in practice at present. The schematic of the cutting process of ODC is shown in Fig. 1. As the cutter is installed eccentrically on the spindle, the cutting process of ODC is discontinuous. The oscillating impact on rock results in tensile cracks with short contact time. Besides, ODC can revolve around its axis caused by friction, so that it wears evenly to increase the service life of the cutter. It combines the advantages of a chisel pick (low thrust force) and a rolling disc cutter (high wear resistance). However, the complexity and low production rate of the machine-assembled ODC limited its application. Consequently, more work should be done to study the cutting mechanics of ODC to improve the structure of the excavation machine. ODC was first applied to mining machinery by CRCMining2 in the early 1990s, and has recently garnered increasing attention for hard rock excavation applications. The ODC technology was implemented in Joy Global’s hard rock mining machine, i.e. Dynacut. Subsequently, Sandvik Ltd. Introduced the MX650, a hard rock excavation machine featuring multiple ODCs, as depicted in Fig. 2a, which utilized large eccentricities and low rotation frequencies for enhanced performance. Contrastingly, Komatsu Ltd. introduced the MC51 hard rock excavation machine in 2021, which employs a single ODC. This design is characterized by its small eccentricity and high rotation frequency, as illustrated in Fig. 2b.

Fig. 1
figure 1

Schematics of ODC cutting process.

Full size image
Fig. 2
figure 2

Excavation machine with ODC technology.

Full size image

From the perspective of rock cutting mechanics with ODC, Hood et al.3, Pickering et al.4,5 and Karekal6 investigated the cutting parameters on the cutting performance of ODC by experiments. The results consistently implied that oscillation can efficiently reduce the cutting force of the disc cutter. Hood et al.7 theoretically studied the crack propagation and failure process during cutting with ODC, but the authors did not consider the kinematics of the cutter. Dehkhoda et al.8 proposed a theoretical model to estimate the cutter forces based on kinematical and geometrical analysis of ODC. This model was built by calculating the contact surface between the cutter and rock coupling with the simple cutter/rock interaction models to estimate the cutter forces. Then they conducted a series of cutting tests on limestone with ODC to assess the prediction and validate the assumptions of this theoretical model9. Subsequently, Dehkhoda et al.10 improved the theoretical model by taking cutter clearance angle into consideration, and obtained the extended model taking into account the variation of cutting depth in estimating cutter forces. Based on the ultimate strength of unit fracture surface and the criterion of minimum energy method, Liu et al.11 proposed the theoretical cutting model of ODC. The dynamic relationship between the caving area of rock and the equivalent caving angle is analyzed, which provides a basis for optimizing the tool structure. This research only concerned the axial vibration of the disc cutter, and the effect of the radial vibration on rock breaking was not considered. Liu et al.12 studied the effects of multi factors on the load spectrum by experiments, and established the models between the radial, axial and total forces of the disc cutter and the feed speed, amplitude and frequency. Subsequently, they constructed the rock cutting model of ODC with inclined tool posture, and analyzed the correlation between cutting force characteristics and rock breaking characteristics and rock breaking mode under different cutting posture inclination angles through numerical simulation and experiment13. However, the above researches mainly studied the prediction of cutting force and the influence of cutting parameters on cutting force and fracture morphology. The study on the influence of rock properties and kinematic parameters on cutting efficiency of ODC is still insufficient. Based on the cutting parameters and rock properties, the evaluation of cutting efficiency and parameter optimization are of great significance to the engineering application of ODC. With the research of in-situ evaluation technology of rock mass properties14,15,16,17,18,19,20, it provides convenience for the acquisition of rock mechanical properties, especially for deep mining conditions.

This paper aims to investigate the influence of kinematic parameters and rock properties on the cutting process with ODC based on the discrete element method (DEM). It is organized as follows: the rock cutting model was established by a DEM software, i.e. PFC3D, and validated by experiments. The micro parameters of the rock model were calibrated according to rock properties. Furthermore, the effects of kinematic parameters (i.e., eccentric ratio, velocity ratio, cutting depth) and rock properties (i.e., uniaxial compressive strength, Young’s modulus) on ODC cutting force, fracture mode and energy consumption are analyzed. The results of this research will enhance the understanding of the cutting mechanism of ODC, and provide a theoretical foundation for ODC parameter design in practical applications.

Modeling of rock cutting with ODC

Calibration of rock models

Four kinds of hard rocks, i.e. red sandstone, limestone, red granite, and white granite, were selected to study the cutting performance of ODC. The rock samples in dimensions of Φ50 × 100 mm and Φ50 × 25 mm were prepared for uniaxial compressive tests and Brazilian tensile tests, respectively. The failure patterns of these rocks in experimental tests are shown in Figs. 3 and 4. The macro properties of uniaxial compressive strength (UCS), Brazilian tensile strength (BTS), Young’s modulus (E) and Poisson’s ratio (μ) of these rocks were obtained and summarized in Table 1. According to Potyondy21, due to the inherent defects formed by the insufficient restriction of the parallel bond model in PFC2D on the relative rotation between particles, the ratio of UCS to BTS is smaller than the true value. Therefore, the calibrated BTS is larger than that obtained by experiment in Table 1.

Fig. 3
figure 3

Failure patterns in uniaxial compressive tests.

Full size image
Fig. 4
figure 4

Failure patterns in Brazilian tensile tests.

Full size image
Table 1 Macro properties of rock samples obtained by experiment and simulation.
Full size table

The particle flow code in three dimensions (PFC3D) was used for rock cutting simulation, and the parallel bond contact model was used for modeling rock samples. The calibration is a process of trial and error by simulating the uniaxial compressive test and Brazilian tensile test shown in Fig. 5 to match the macro properties. The details of the calibration process can be referred to Lei et al.22 and Li et al.23. The macro properties and micro parameters of these four kinds of rocks are summarized in Tables 1 and 2, respectively.

Fig. 5
figure 5

DEM models for calibration of micro parameters.

Full size image
Table 2 The calibrated micro parameters of rock models.
Full size table

Rock-cutting model

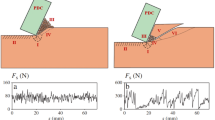
The rock-cutting model with ODC is established by PFC3D as depicted in Fig. 6. The rock model dimensions conform to a 300 mm length, 200 mm width, and 100 mm height, with a hierarchical structure implemented to enhance both simulation accuracy and computational efficiency. The radii of the outer and inner particle layers range between 3.5 ~ 4.5 mm and 1.5 ~ 2.0 mm, respectively, totaling 40,603 particles within the rock model. The ODC is represented as a rigid wall element with a specified radius of 50 mm. During the simulation, comprehensive data including three-dimensional cutting forces, generated cutting chips, and the entire cutting sequence are recorded. Post-simulation, the torque (T) experienced by the ODC and the specific energy (SE) are computed using Eqs. (1) and (2). The SE, a pivotal metric in assessing the efficacy of excavation tools, quantifies the energy required per unit volume of rock excavated, thereby offering insights into the cutting process’s efficiency.

$$T = Fy \cdot e\sin \theta + Fx \cdot e\cos \theta$$
(1)
$$SE = \frac{{T_{m} \cdot \Theta }}{V}$$
(2)

where Fy and Fx are cutting forces along X-axial and Y-axial, e is the eccentricity, θ is the position angle, Tm is the mean torque, Θ is the total rotation angle, V is the volume of rock fragments.

Fig. 6
figure 6

Cutting model with ODC established by PFC3D.

Full size image

Validation of the rock-cutting model

Laboratory set-up with ODC

The rock-cutting tester with ODC is depicted in Fig. 7 developed based on a full-scale linear rock-cutting testing system fabricated by the Collaborative Innovation Center for Intelligent Mining Equipment at China University of Mining and Technology. Figure 8 illustrates the detailed schematics of the testing apparatus alongside the ODC mounting assembly. The eccentric rotation of ODC is obtained by the eccentric shaft sleeve. The experimental setup employs an ODC with a specified radius of 50 mm. The tester is designed to accommodate rock specimens with dimensions reaching 1.0 m in length, 0.7 m in both width and height. The forces exerted during cutting are captured by a high-capacity 3D force sensor capable of measuring up to 50 tons. Additionally, a torque sensor, sensitive up to 200 Nm, is employed to quantify the torque experienced by the ODC. Cutting dynamics, including forces, torque, and displacement, are logged via a data acquisition system, which also governs the test parameters such as cutting direction and velocity. The system has a sampling frequency adjustable up to 1 MHz, ensuring comprehensive and precise data capture.

Fig. 7
figure 7

Photo of the rock-cutting tester with ODC.

Full size image
Fig. 8
figure 8

Schematics of the cutting tester and ODC holder.

Full size image

Validation by rock cutting tests

According to Dehkhoda8, two dimensionless parameters, i.e. eccentric ratio (RE) and velocity ratio (RV), are used for reducing the variables and facilitating analysis. RE is a scaled eccentricity and 2πRV represents the average penetration per revolution scaled by the eccentricity (e). RE and RV are calculated as Eq. (5). In the experiments, the constant is RE of 0.02. The variables are RV and cutting depth (d) listed in Table 3. The mean cutting force and mean torque of ODC are calculated and summarized in Tables 3 and 4. Figures 9 and 10 show the correlation relationships of the mean cutting force and mean torque between the experiment and the simulation. Although the mean cutting force and mean torque of the simulation are less than the experimental results, linear relationships are found between the experimental and the numerical results. Consequently, it’s valid and reasonable to investigate the influence of kinetic parameters of ODC on cutting performance using this DEM cutting model.

$$\left\{ \begin{gathered} R_{E} = \frac{e}{a} \hfill \\ R_{V} = \frac{v}{e\omega } \hfill \\ \end{gathered} \right.$$
(5)

where e is the eccentricity, a is the radius of ODC, ω is the rotation speed and v is the cutting velocity.

Table 3 Mean cutting forces obtained from experiment and simulation.
Full size table
Table 4 Mean torque of ODC obtained from experiment and simulation.
Full size table
Fig. 9
figure 9

Correlation relationship of mean cutting forces obtained from experiment and simulation.

Full size image
Fig. 10
figure 10

Correlation relationship of mean torques obtained from experiment and simulation.

Full size image

Numerical simulation and discussion

The numerical simulations are divided into two groups. The parameters are listed in Table 5. In the first group, the rock sample is red sandstone. The variables under examination include eccentricities of 1.0, 2.5, and 4.0 mm, alongside rotation speeds ranging from 125 to 1250 rad/s in increments of 250, 200, 300, and 500 rad/s, with the aim of elucidating the effects of RE and RV on the rock cutting performance. To maintain experimental consistency, constant parameters are set as follows: a uniform cutting depth of 5 mm, an ODC radius of 50 mm, and a consistent cutting speed of 250 mm/s. In the second group, the variables are rock types and cutting depth of 3, 5, 10, 12, and 15 mm to investigate the influence of rock properties and cutting depth on cutting performance. The constants are set at an eccentricity of 1.0 mm and a rotation speed of 500 rad/s with all other parameters remaining consistent with those of the first group.

Table 5 Summary of simulation experiment parameters.
Full size table

Influence of R E and R V on cutting performance

The eccentric ratio (RE) and velocity ratio (RV) are the main parameters affecting the cutting performance of ODC8. The first group of simulations listed in Table 5 is conducted to investigate the influence of RE and RV on cutting forces, crack count, and specific energy. Taking the cutting condition of RE = 0.02, RV = 0.5, and d = 5 mm as an example, Fig. 11 illustrates the detailed evolution of cutting force and torque experienced by the ODC, with a focus on the magnified initial crushing phase. During the initial crushing phase, there are two primary peaks in the curves representing two separate instances of rock being crushed. The pre-peak phase is characterized by a pronounced fluctuation in cutting force, particularly notable in the vicinity of the peak. During this phase, microfractures are initiated ahead of the cutter. Subsequently, a rapid decline in cutting force accompanies the generation of substantial chips, suggesting the brittle fracture mode of red sandstone.

Fig. 11
figure 11

Curves of cutting force and torque with an enlarged display of the first crushing process in the condition of RE = 0.02, RV = 0.5, and d = 5 mm.

Full size image

The mean cutting force (Fm) and mean torque (Tm), under different cutting conditions were calculated. The impact of RE and RV on cutting forces exhibits comparable trends, as depicted in Fig. 12. Both Fm and Tm demonstrate an ascending trajectory with the increase of RE and RV. Nevertheless, a notable shift occurs in the increasing rate of Fm with RV beyond 0.5, which progresses at a more gradual pace. This phenomenon can be attributed to an extended contact duration between ODC and the rock, which mitigates the immediacy of impact. Under continuous contact conditions, the cutting dynamics resemble those of a chisel pick or conical pick.

Fig. 12
figure 12

Influence of RE and RV on (a) mean cutting force and (b) mean torque.

Full size image

The fracture patterns of red sandstone under different cutting conditions are shown in Fig. 13. The red disks and yellow disks are shear fractures and tensile fractures in the graph, respectively. The blue disks are particles displayed in the section view across the rock model. According to the graphs, there are many micro-fractures in front of ODC. As the shear strength is less than the tensile strength of bonds between particles, the crush zone is composed of shear fractures primarily company with few tensile fractures. According to Fig. 13a, when RV is constant, the crush zone increases with the increase of RE and extends along Y and Z axes. When RE is constant, the strain inside the rock model increases with the increasing RV shown in Fig. 13b. It suggests that more energy is consumed in the form of accumulated strain energy in the condition of high cutting velocity or low rotation speed.

Fig. 13
figure 13

Fractures and stress distribution under different cutting conditions.

Full size image

The count of micro fractures during cutting is recorded shown in Fig. 14. The fracture count exhibits a stepwise increment, suggesting the concurrent generation of fractures, followed by a phase of particle separation with limited fracture formation. It is consistent with the process of rock fragmentation. Before rock fragmentation, the cracks are initiated and propagate company with fracture formation and cutting force increasing (Fig. 11) till the fragment is separated from the rock mass. As shown in Fig. 14a, the length of steps in the curves increases with the increase of RE suggesting that fewer but larger chips are formed with large eccentricity. However, RV has little influence on the fracture count according to Fig. 14b. From the specific energy (SE) perspective, SE increases with the increase of RV and RE shown in Fig. 15. As analyzed above, more energy is consumed in the form of accumulated strain energy rather than broken rock with the increasing RV which results in the reduction of impact effect and the increase of SE. Although an enlarged RE contributes to the formation of larger chip segments, the cutting force demonstrates a disproportionately rapid escalation relative to the growth in chip volume, consequently resulting in elevated SE.

Fig. 14
figure 14

Curves of fracture count during the cutting process.

Full size image
Fig. 15
figure 15

Relationships between specific energy and RV, RE on red sandstone.

Full size image

Influence of cutting depth on cutting performance

The simulations investigating the impact of cutting depth on cutting performance have been conducted on red sandstone. The relationships between cutting depth and mean cutting force, and mean torque are illustrated in Fig. 16. The graph shows that mean cutting force and mean torque increase with cutting depth. And the linear relationships are found with correlation coefficients of R2 ≥ 0.813. Figure 17 shows the curves of cutting forces and fracture count in the initial crushing phase. According to these figures, there are high correlation between fluctuation characteristics of cutting force and fracture count. The peak cutting forces appear at the start of the rising side of the steps in the curve of fracture count. It suggests that the cutting force is maximum at the crack initiation stage and decreases during crack propagation which is consistent with the analysis of Li et al.24. Besides, the curves of cutting force and fracture count become smooth shown in Fig. 17c due to the fracture mode changes from ductile to brittle company with fewer tiny chips in the condition of large cutting depth25.

Fig. 16
figure 16

Relationships between cutting depth and mean cutting force, mean torque.

Full size image
Fig. 17
figure 17

Curves of cutting forces and fracture count in the first crushing process under different conditions of cutting depths.

Full size image

The fractures and stress distribution with different cutting depths are shown in Fig. 18. It can be seen that with the increase of cutting depth, the crushing zone beneath ODC expands towards the interior and sides of ODC. Combined with the cutting force curve (Fig. 17), with the increase of cutting depth, the cutting force curve tends to be smooth, indicating that the formation of large chips increases, and the rock fracture mode transitions from ductile to brittle. Although the cutting force increases with the increase of cutting depth, the proportion of large chips increases, which reduces the surface energy consumption. Therefore, the specific energy (SE) decreases with the increase of cutting depth shown as Fig. 19.

Fig. 18
figure 18

Fractures and stress distribution with different cutting depths.

Full size image
Fig. 19
figure 19

Relationship between SE and cutting depth for red sandstone.

Full size image

Influence of rock properties on specific energy

The investigation into the effects of rock properties on specific energy (SE) during ODC cutting has been undertaken through simulations with different rock types. Figure 20 shows the relationships between SE and UCS, E with different cutting depths. The figures illustrate that SE exhibits a positive correlation with UCS and E, whereas it demonstrates an inverse relationship with the cutting depth. As analyzed in Sect. 4.2, the rock fracture mode transitions from ductile to brittle as the cutting depth increases, which consequently leads to a reduction in the proportion of fine chips produced. Consequently, less energy is consumed to generate new surface leading to the decrease of SE. Besides, SE exhibits a strong linear correlation with E, whereas SE increases exponentially with the increase of UCS. Consequently, the elastoplastic properties of the rock are more suitable to evaluate the cutting efficiency of ODC. However, for conical picks, the linear relationships were found between SE and UCS, BTS while nonlinear relationships were obtained between SE and other properties26. From the perspective of the interaction process, it can be concluded that the oscillation impact process with ODC is proportionally related to E, while the continuous cutting process with a conical pick is proportionately related to strength properties, i.e. UCS, BTS. The relational equations of SE and cutting depth, UCS, and E are obtained by multiple regression analysis with a correlation coefficient of R2 > 0.8 as shown in Fig. 21.

Fig. 20
figure 20

Relationships between specific energy and UCS, E

Full size image
Fig. 21
figure 21

Multiple regression analysis between SE and cutting depth, UCS and E.

Full size image

Conclusions

This study establishes a numerical rock-cutting model of oscillation disc cutter (ODC) using PFC3D, validated through experimental verification, to investigate its unique tensile fracture mechanism and cutting efficiency. Three fundamental findings emerge from the analysis:

  1. (1)

    The eccentric ratio (RE) and velocity ratio (RV) demonstrate proportional relationships with specific energy (SE). Increasing RE from 0.02 to 0.08 raises SE from 0.40 to 21.2 MJ/m3 due to accelerated cutting force escalation despite reduced chip quantity. Simultaneously, higher RV extends tool-rock contact duration, promoting strain energy accumulation over fracture generation. These findings suggest optimal operation within RE = 0.02–0.05 and RV = 0.08–0.45 ranges to balance cutting efficiency and energy expenditure.

  2. (2)

    Positive linear correlations between cutting force (R2 = 0.81), torque (R2 = 0.95) and cutting depth were obtained. Fracture evolution analysis identifies distinct stages: the peak cutting forces occur during crack nucleation, followed by the reduction of cutting force during propagation. The fracture mode transitions from ductile to brittle with increasing cutting depth, accompanied by the reduction of SE.

  3. (3)

    Multiple regression analysis establishes SE = 14.98 − 0.26UCS − 0.39d + 0.002UCS2 + 0.011d2 (R2 = 0.84) and SE = 1.672 + 0.117E − 0.2d (R2 = 0.82), where UCS and E show exponential and linear influence on SE, respectively.

These results provide theoretical foundations for ODC system optimization, particularly in matching kinematic parameters with geological conditions. Future research should address scale effects in field applications and tool wear patterns under prolonged operation.