Hybrid physics-AI outperforms numerical weather prediction for extreme precipitation nowcasting

Abstract

Precipitation nowcasting, which is critical for flood emergency and river management, has remained challenging for decades, although recent developments in deep generative modeling (DGM) suggest the possibility of improvements. River management centers, such as the Tennessee Valley Authority, have been using Numerical Weather Prediction (NWP) models for nowcasting, but they have been struggling with missed detections even from best-in-class NWP models. While decades of prior research achieved limited improvements beyond advection and localized evolution, recent attempts have shown progress from so-called physics-free machine learning (ML) methods, and even greater improvements from physics-embedded ML approaches. Developers of DGM for nowcasting have compared their approaches with optical flow (a variant of advection) and meteorologists’ judgment, but not with NWP models. Further, they have not conducted independent co-evaluations with water resources and river managers. Here we show that the state-of-the-art physics-embedded deep generative model, specifically NowcastNet, outperforms the High Resolution Rapid Refresh (HRRR) model, which is the latest generation of NWP, along with advection and persistence, especially for heavy precipitation events. Thus, for grid-cell extremes over 16 mm/h, NowcastNet demonstrated a median critical success index (CSI) of 0.30, compared with median CSI of 0.04 for HRRR. However, despite hydrologically-relevant improvements in point-by-point forecasts from NowcastNet, caveats include overestimation of spatially aggregate precipitation over longer lead times. Our co-evaluation with ML developers, hydrologists and river managers suggest the possibility of improved flood emergency response and hydropower management.

Introduction

Flooding, a prevalent weather hazard, impacts numerous regions globally, causing economic damage and disruption each year. In the United States alone, between 1980 and 2019, flooding resulted in losses totaling $146.5 billion and claimed the lives of 555 individuals, as reported by NOAA’s National Centers for Environmental Information¹. The impacts of floods and especially flash floods extend beyond immediate human and infrastructural losses to encompass critical infrastructure such as hydropower operations and dam management². In the Southeastern United States (SEUS), flash floods are a major concern due to their sudden and severe nature^3,4. The Tennessee Valley Authority (TVA), which manages the Tennessee River system in Tennessee and six surrounding states in the SEUS, has to often deal with flash floods, primarily triggered by mesoscale convective systems (MCSs). A noteworthy example is the devastating flood in middle Tennessee, in August 2021, which resulted in the loss of 20 lives and more than $100 million in property damage⁵. Similarly, the Damodar Valley Corporation, modeled after the TVA⁶, manages the Damodar River in West Bengal, India, and has been struggling with unpredictable floods⁷ despite infrastructural advancements. Other examples of river management centers dealing with deadly flash floods includes the Società Adriatica di Elettricità in Italy (1963 Vajont Dam failure, 2000 people killed)⁸, the Nile River Basin Authority in Egypt (2015 Alexandria and Nile Delta floods, 17 deaths)⁹, and the Kerala Water Resources Department in India (2018 flood in Kerala, 400 deaths)¹⁰. To address the challenges posed by emergency flash flood management, short-term Quantitative Precipitation Forecasts (QPF) serve as vital tools by driving the hydrologic and hydraulic models which predict runoff and flooding downstream^11,12. Traditional forecasting methods have employed persistence, advection of radar echoes¹³, Numerical Weather Prediction (NWP) models¹⁴, and data-driven extrapolation-based methods¹⁵, either individually or in combination¹⁶. Although short-term QPFs offer well-documented advantages, this field has long been acknowledged as one of the most challenging in hydrometeorology. Even leading NWP models such as High Resolution Rapid Refresh (HRRR), often struggle to accurately predict extreme precipitation events^17,18, prompting organizations like the TVA to opt for alternative forecasts with coarser spatial and temporal resolution. However, in recent years, with advancements of machine learning, studies have demonstrated that deep learning methods can surpass traditional approaches like persistence, advection, and optical flow^16,19,20,21.

Current machine learning methods treat forecasting as an image-to-image translation problem, employing computer vision tools to generate nowcasts²². The latest development in such physics-free nowcasting approaches comes from Google DeepMind²³. Their physics-free AI model, known as Deep Generative Model of Rainfall (DGMR), is trained on historical weather data and can rapidly analyze patterns and make predictions without explicit knowledge of atmospheric physics. However, while DGMR offered accurate forecasts in comparison to previous methods, it struggled to accurately predict extreme precipitation events²⁴. A more recent study improved nowcasting of extreme precipitation by combining physical-evolution schemes such as the conservation of mass for precipitation fields over time and space and conditional-learning methods into a neural-network framework called NowcastNet²⁴. It addresses both advective and convective processes, which was previously deemed challenging in DGMR.

In this study, we assess the performance of the state-of-the-art physics-conditioned deep generative model in predicting precipitation patterns during record-breaking flood events as well as heavy precipitation events in the Tennessee Valley. Due to its exposure to extreme storms and extensively dammed rivers, the Tennessee Valley is a critical focus area for evaluating NowcastNet’s effectiveness in flood prediction and disaster management. In this study, we evaluate the following methods:

• NowcastNet²⁴, state-of-the-art physics embedded DGM, provides forecasts at 10 min interval for 3 h at 1 km resolution. NowcastNet merges convective-scale details observed through radar data with mesoscale patterns dictated by physical laws into a neural-network framework.

• High Resolution Rapid Refresh (HRRR)^25,26, state-of-the-art NWP model, developed by NOAA, provides hourly forecasts at 3 km resolution utilizing complex physics based equations and data assimilation.

• Baseline approaches:

  • — Advection or Optical Flow, represented by the PySTEPS²⁷ algorithm, which uses an advection scheme influenced by the continuity equation. It predicts future motion fields and intensity residuals by iteratively advecting past radar data.

  • — Persistence, which assumes precipitation intensity and location will remain the same over increasing lead time.

While developers of physics free or physics-conditioned deep generative models of nowcasting, have compared their approaches with optical flow in terms of skill scores as well as judgment of meteorologists, they have not compared with NWP models and did not do independent evaluations for hydrologic use. This study compares NowcastNet with HRRR, which is widely used in many river basins^28,29 but has not previously been evaluated against NowcastNet. Although there are studies comparing deep learning models with NWP models for precipitation forecasting¹⁷, these comparisons often overlook the differences in phenomenon space and time scales. Earth system prediction problems vary depending on these scales, and challenges in weather and hydrological forecasting cannot be directly compared across different space-time scales³⁰.

Accurate nowcasting impacts integral areas in hydrology such as river management, dam operations, and flash flood prediction, which affect the lives and property of human directly. We evaluated NowcastNet using extreme storms relevant to the stakeholders, employing both standard skill metrics and hydrologically relevant metrics co-developed with river managers. Skill scores measure how well the model’s predictions outperform a baseline or reference model and are essential for early detection and issuing emergency alerts like flood warnings. However, for predicting exact flood levels or calculating the specific volume of water to release from a dam, error-based metrics are crucial. We also employ the Contiguous Rainfall Area (CRA) method to break down errors into pattern, volume, and displacement components, providing a detailed understanding of where predictions diverge from observed events. Additionally, the use of median, quartiles, and outliers of scores quantifies uncertainty across extreme storms in the TVA region, giving river managers insights into the reliability of forecasts and helping them respond effectively to future events. These approaches ensure that the model’s predictions are not only timely but also accurate, thereby enhancing reliability and minimizing the risk of false alarms or missed events, ultimately contributing to the development of trustworthy AI in hydrologic management.

Results

Tennessee Valley Authority case study

The TVA plays a pivotal role in flood control, navigation, power generation, water supply, water quality maintenance, and recreation across the Tennessee River system in the Southeastern US and the Appalachian region. They manage a vast river network spanning approximately 640 miles and encompassing around 40,000 square miles of watershed. TVA manages 49 dams, 29 of which produce hydroelectricity, and they provide electricity to 153 local power companies, serving more than 10 million people. Moreover, with strategically constructed dams and reservoirs along major river systems like the Tennessee River, TVA regulates water flow to mitigate flood risks during heavy rainfall and storm events. In Fig. 1, the operating area of TVA is shown with the locations of key electricity generating facilities.

Fig. 1: Map depicting the Tennessee Valley Authority (TVA) service area and the locations of key electricity generating assets within the region.

The figure provides an overview of the geographical coverage of TVA's operations and highlights the distribution of major power generation facilities as reported by the Government Accountability Office (GAO) in their 2023 Report to Congressional Requesters⁶².

In the Tennessee Valley, floods are primarily triggered by mesoscale convective systems (MCSs), mid-latitude cyclones (MLC), and tropical storm remnants (TSR), either individually or in combination. Despite advancements in weather prediction models, several flood instances revealed limitations in forecasting intensity and location accurately. A pertinent case study is the devastating August 2021 flood in Waverly, Tennessee. The flood event was triggered by unprecedented rainfall and the deluge, attributed to a complex interplay of meteorological phenomena, highlighted vulnerabilities in flood preparedness and response mechanisms. Despite prior warnings issued by the National Weather Service, the rapid onset of the flood prevented timely evacuation efforts, exacerbating the impact on residents. Meteorological observations indicated an abundance of atmospheric moisture, along with the interaction between a mid-level warm front and a stationary front over West Tennessee, creating conditions conducive to intense precipitation and subsequent flooding. The mesoscale convective system responsible for the event showcased the heightened vulnerability to extreme weather events, emphasizing the imperative for robust flood management strategies and precise forecasting methods to mitigate future risks. While this event occurred in an unregulated part of the basin, it underscores the potential for similar catastrophic events across the TVA region. TVA holds its dam reservoirs at a high water level in the summer, as part of its multi-objective optimization, including recreation and seasonal electricity demand. These elevated water levels would have constrained the time available for emergency response if the event had happened in a regulated section of the system. Thus, accurate forecasts would have been crucial in managing or mitigating the flood impact, emphasizing the significance of timely predictions. Therefore, the Waverly flood event emphasizes the intricate relationship between meteorological dynamics and human vulnerability, prompting TVA to prioritize high-quality hourly forecasts and consistent predictions for extreme events.

Following the Waverly event, questions arose regarding the effectiveness of the HRRR model, used by TVA and other agencies to predict weather patterns and assess flood risks. While the HRRR model provided valuable insights into typical weather conditions, its performance during the Waverly event cast doubt on its reliability during extreme events. Here, Fig. 2 shows the performance of the HRRR model during the Waverly event on August 21, 2021. The figure reveals the disparity between the predicted accumulated precipitation and the observed values at the McEwen gauge, shedding light on the forecast bias. The McEwen gauge station was chosen for this analysis due to its reliable ground-based observations near the Waverly storm, setting a Tennessee record with 17 inches of rainfall in 24 h³¹. Moreover, the data from this gauge was specifically recommended by TVA managers, further validating its relevance to our analysis and the McEwen precipitation accumulation data utilized in this comparison is derived from TVA-collected data. Around 11:00 UTC, when the actual rainfall accumulation reached a cumulative 13 inches, the HRRR forecasted only 2 inches. Similarly, despite a total rainfall of 17 inches throughout the day in McEwen, the HRRR model predicted only 4 inches.

Fig. 2: Comparison of accumulated precipitation forecasts from High-Resolution Rapid Refresh (HRRR) model at the McEwen precipitation gauge during the Waverly event provides insights into the forecast bias.

Precipitation forecasts (in inches) on August 21, 2021, displayed in Coordinated Universal Time (UTC) from the High-Resolution Rapid Refresh (HRRR) model, are shown with red, yellow, and green lines, while observations are shown with a blue line. The McEwen precipitation accumulation data utilized in this comparison is derived from TVA-collected data. The plot illustrates the discrepancy between the accumulated precipitation forecasts and the actual observations at the McEwen gauge.

More information about other heavy precipitation events and HRRR’s failure to accurately forecast the events are given in Supplementary Information Section A. Beyond assessing the Waverly event, we considered 30 additional extreme precipitation events (with grid cells exceeding 30 mm/h) occurring between January 2021 and April 2024, specifically within the TVA area. The list of the events is given in Supplementary Information Section (Table S1). These events are selected based on the catastrophic impacts they had in the TVA region.

Performance of physics conditioned deep generative model: NowcastNet

The performance of the NowcastNet model during the Waverly event (August 21, 2021) is evaluated within the TVA area. Multi Radar Multi Sensor (MRMS) data are used as reference observations which is developed by NOAA’s National Severe Storms Laboratory (NSSL) and it incorporates data from approximately 180 operational US WSR-88D weather radars and model analyses to produce gridded precipitation³². Detailed information on the dataset and NowcastNet model is given in the “Methods” section and Supplementary Information Section B, including how the model has incorporated physics and its training and evaluation datasets. The steps to apply the NowcastNet model in the TVA region are described in Supplementary Information Section C. Figure 3 presents precipitation predictions starting from 9:00 UTC (T + 1 h) until 11:00 UTC (T + 3 h) from both the NowcastNet model and HRRR forecasts, along with the Power Spectral Density (PSD) performance metric.

Fig. 3: Comparison of precipitation forecasts from NowcastNet and HRRR for the Waverly flood event (August 21, 2021): spatial accuracy and power spectral density analysis.

Precipitation forecasts (in mm/h) from NowcastNet (1 km spatial resolution) and HRRR (3 km spatial resolution) at different lead times (T + 1 h, T + 2 h, and T + 3 h) with MRMS QPE³² for the Waverly flood event on August 21, 2021 (T = 8:00 UTC) within the TVA area. The precipitation images cover a spatial extent of 384 km × 384 km. The base map shows US state boundaries. NowcastNet predicts the MRMS precipitation patterns more closely than HRRR does, in terms of the spatial distribution and intensity of the precipitation. The last row depicts the PSD at different wavelengths, at different lead times (T + 1 h, T + 2 h, and T + 3 h).

The Waverly event is characterized by its extreme precipitation, which stemmed from a mesoscale convective system, a collection of thunderstorms. Capturing extreme precipitation at convective scales is challenging due to the rapid development, intensity, and localized nature of convective storms. Despite the challenges, NowcastNet predicted the hotspots of extreme precipitation locations of more than 30 mm/h more accurately than HRRR. For the 3-h forecasts, NowcastNet is capable of forecasting the trajectory of the thin line of convective precipitation, whereas HRRR could not predict the heavy precipitation at all. The PSD reveals strength of a signal as a function of spatial scale, and for this case study the PSD curve of the forecast matches the PSD curve of the MRMS for wavelengths 4 km to 16 km, and the nowcast only slightly overestimates PSD for the rest of the wavelengths from 2 km to 256 km. Even at 3 h lead time, although the two PSD curves are slightly off at wavelengths greater than 16 km or less than 4 km, it is a near-exact match for wavelengths between 4 km and 16 km, indicating that the forecast contains the same amount of information detail as the MRMS at these spatial scales. On the other hand, the information content in the HRRR does not match the observed QPE at any wavelength. Although, NowcastNet displays the right amount of detail at most spatial scales, with increasing lead time, the model exhibits broader areas of light precipitation, leading to challenges in precisely identifying the exact location of precipitation.

To provide a more comprehensive evaluation of the model’s performance, we expanded the analysis to consider multiple initialization times, similar to the approach used in Fig. 2. Supplementary Fig. S1 shows accumulated precipitation forecasts (hourly) from both the NowcastNet and HRRR models at various initialization times (08-20-2021 13:00 UTC to 08-22-2021 07:00 UTC) with underestimation of forecasts shown with positive bias and overestimation shown with negative bias during the Waverly event. The NowcastNet forecast closely follows the observed precipitation trend, capturing the timing and intensity of the rainfall with minimal bias. However, there is a slight underestimation towards the end of the storm event. The HRRR forecast significantly underestimates the precipitation throughout the event, as shown in Fig. 2.

The performance of NowcastNet was compared against HRRR as well as persistence and advection. Advection is represented by the PySTEPS²⁷ algorithm (Supplementary Information Section D). For comprehensive evaluation, 30 heavy precipitation events from January 2021 to April 2024 are examined in this study. Among them, the performance of NowcastNet against MRMS, HRRR, persistence, and advection is highlighted for 4 events and shown in Supplementary Figs. S2–S5. In all the events, NowcastNet exhibits a higher degree of similarities to MRMS. In contrast, HRRR encounters challenges in capturing finer details when compared to MRMS. Persistence assumes precipitation intensity and location will remain the same over time, and likewise we see its performance deteriorate over time. On the other hand, the advection model illustrates the movement but fails to capture the intensities of extreme precipitation and produces blurry nowcasts.

Various metrics were employed to evaluate NowcastNet’s predictions against HRRR in these events. These metrics help determine the model’s ability to classify and predict the occurrence and intensity of precipitation events, as well as how well the models predict continuous variables related to hydrological processes, such as rainfall amounts and their spatial distribution. The spatial resolution of MRMS and NowcastNet is finer (1 km) than HRRR (3 km). Here, for fair comparison, the MRMS QPEs and NowcastNet forecasts were upscaled to 3 km. Persistence and advection forecasts were also analyzed at 3 km spatial resolution. In this study, we have used 3 thresholds (t) for extreme precipitation events, t > 0.1 mm/h, t > 16 mm/h, and t > 32 mm/h for all categorical skill scores. We have chosen 16 mm/h and 32 mm/h because they are standard benchmarks used to define extreme events in the literature²⁴. The skill score metrics presented here include pixel-based metrics such as probability of detection (POD), false alarm ratio (FAR), and critical success index (CSI), along with a neighborhood-based metric, fractions skill score (FSS) (Fig. 4). POD and FAR are particularly important for conveying the performance of these models to river managers, CSI is chosen because it is a standard metric used in the evaluation of state-of-the-art models^23,24, and FSS with 9 km × 9 km neighborhood is included to provide insight into neighborhood-based skill, as using only grid-point verification can yield misleading results due to double-penalty errors, where forecasts are penalized twice for deviations caused by displacement errors³³. River managers and dam operators need to focus on the smallest neighborhood that still provides meaningful area-based evaluations. Thus, we have selected a 3 × 3 pixel neighborhood (i.e., a 9 km by 9 km area), which corresponds to the smallest possible neighborhood. However, to understand how skills change with larger neighborhoods, we have compared the NowcastNet model with MRMS (observations) across multiple neighborhood sizes, as shown in Supplementary Figs. S9 and S10. Figure 4 shows box plots of all these metrics for different lead times and for all 3 thresholds. The median, quartiles, and outliers of scores provide uncertainty quantification across 30 extreme storms from the TVA region, giving river managers vital information on how to trust and react to each model’s forecast during a future extreme storm. Here, for all lead times, all thresholds, and all metrics, NowcastNet outperforms HRRR, with better median scores across the 30 events. Although NowcastNet’s performance declines at longer lead times for more extreme thresholds, it still outperforms HRRR and persistence, which have the worst scores. At the T + 1 h lead time and for the t > 0.1 threshold at longer lead times, NowcastNet’s superiority over HRRR is clear.

Fig. 4: Metrics comparison across 30 heavy precipitation events.

Comparison of precipitation forecast accuracy between NowcastNet, HRRR, Persistence, and Advection against MRMS QPE (at 3 km spatial resolution) for 30 heavy precipitation events across the geography of interest. Metrics include Critical Success Index (CSI), Probability of Detection (POD), False Alarm Ratio (FAR), and Fractions Skill Score (FSS); all at thresholds (t) of t > 0.1 mm/h, t > 16 mm/h and t > 32 mm/h for different lead times (T + 1 h, T + 2 h, and T + 3 h). Upward arrow indicates higher score is better and downward arrow indicates lower score is better.

Across nearly all metrics and thresholds, the quartiles, minimum, and maximum of NowcastNet scores are better than those of HRRR, indicating an advantage not just for the median but for most storms. Aside from superiority over HRRR, we see that NowcastNet performs better than the baseline methods in terms of CSI, FAR and FSS, but the advection model shows better performance in terms of POD, highlighting its strength in capturing the movement of precipitation, albeit with less accuracy in predicting its intensity. HRRR might perform better at longer lead times with sufficient spin-up time for data assimilation, but this scenario was not tested in our study. This quantitative evaluation emphasizes NowcastNet’s effectiveness relative to HRRR and other baseline methods in predicting extreme precipitation events’ intensity and location across the forecast intervals. We also evaluated additional commonly used skill score based metrics, including the F1 Score, Equitable Threat Score (ETS), and Heidke Skill Score (HSS) (Supplementary Fig. S6), all of which corroborated the findings of our primary analysis.

Apart from skill scores, we also employed error and correlation based metrics for comprehensive assessment in Supplementary Fig. S7. Metrics included here are RMSE, Inverse NMSE, Numerical Bias, Normalized Error, and Pearson’s Correlation. Metrics are calculated at pixel level, and they provide insights into how well each forecasting method predicts precipitation amounts compared to observed values. Findings from these metrics show that NowcastNet outperforms HRRR and baseline methods at the 1-h lead time for all metrics, demonstrating its strength in short-term precipitation forecasting accuracy. NowcastNet more accurately captures the timing and magnitude of precipitation events, resulting in lower residuals compared to other models. Notably, NowcastNet maintains a better correlation with MRMS at all lead times, while the median HRRR forecasts exhibit zero correlation. However, NowcastNet tends to overestimate precipitation, particularly at longer lead times, which affects error metrics such as RMSE and numerical bias. Despite this overestimation, the model effectively aligns with overall trends in the data, highlighting its reliability in short-term precipitation forecasts. In contrast, HRRR shows better performance than NowcastNet at longer lead times (2–3 h) in terms of RMSE, Inverse NMSE, and Normalized Error, likely due to NowcastNet’s tendency to overestimate precipitation more frequently than HRRR.

To assess NowcastNet’s predictive capabilities at 1 km spatial resolution against MRMS QPE, the set of skill score based metrics is employed at 10-min intervals for three thresholds. In Supplementary Fig. S8, the metrics are plotted against different lead times. The shaded range in the figure shows the maximum and minimum of 30 heavy precipitation events at any given lead time. The results at 10-min intervals show similar trends to those observed at the hourly intervals in Fig. 4), reaffirming the model’s strengths and limitations. However, the 10-min interval forecasts are particularly important for river managers, as they provide more granular and timely information, which is crucial for emergency management and rapid response to changing conditions during extreme weather events. We have also estimated how the neighborhood-based metric, FSS, changes with increasing neighborhood sizes and lead times, demonstrating the NowcastNet model’s performance at spatial resolution of 1 km (Supplementary Figs. S9 and S10). It should be noted that the earlier FSS analysis used 3 km resolution, but because NowcastNet will be used operationally at 1 km resolution, we used 1 km for this supplementary analysis. From this analysis it is evident that FSS score is higher for larger neighborhoods, and for each neighborhood size, a decreasing trend is observed with increasing lead times. These results show that river managers can expect similar forecast dynamics regardless of whether the storm at hand merely requires skill within a large neighborhood, or whether skill in a small neighborhood is strictly required.

For further investigation of the NowcastNet model’s performance in comparison to MRMS QPE, we assessed four extreme precipitation events from 2021 and 2024. The event forecasts are done for August 21, 2021, at 8:00 UTC, February 17, 2022, at 18:00 UTC, February 16, 2023, at 12:00 UTC and March 15, 2024, at 3:00 UTC in the TVA area. Figure 5 illustrates a comparison of precipitation prediction discrepancies from the NowcastNet model at different lead times (T + 10 min, T + 1 h, T + 2 h, and T + 3 h) with MRMS QPE, for the extreme events. The plot shows that, as the lead time increases, discrepancies between MRMS and predictions become more pronounced, indicating the challenges associated with accurately forecasting extreme precipitation events over extended time horizons. We observed areas of underestimation, where NowcastNet either forecast a less-intense event or missed the precipitation event completely, as well as overestimation, where the model predicted high rainfall despite lesser precipitation or lack of it altogether. This suggests that the model’s predictive capability diminishes with longer lead times, leading to larger areas of overestimation of precipitation.

Fig. 5: Precipitation prediction discrepancies from NowcastNet at varying lead times for four extreme rainfall events.

Comparison of precipitation prediction discrepancies (in mm/h) from NowcastNet model at different lead times (T + 10 min, T + 1 h, T + 2 h, and T + 3 h) with MRMS for four extreme rainfall events on August 21, 2021 (T = 8:00 UTC), February 17, 2022 (T = 18:00 UTC), February 16, 2023 (T = 12:00 UTC) and March 15, 2024 (T = 3:00 UTC), within the TVA area. The basemap shows US state boundaries. Blue shades represent underestimation, while red shades represent overestimation of precipitation. With increasing lead time, discrepancies between MRMS and NowcastNet predictions become more pronounced.

To understand the source of these errors, we conducted a detailed analysis using the Contiguous Rainfall Area (CRA) method, which quantifies errors in the predicted location of rain systems by breaking down the total error into components related to location inaccuracies, amplitude discrepancies, and differences in fine-scale patterns^34,35. Figure 6 presents the comparison between observed and forecasted precipitation patterns and the associated error decompositions using the CRA method for the Waverly event (August 21, 2021, 8:00 UTC).

Fig. 6: Comparison of observed and forecast precipitation patterns and error decomposition using the contiguous rain area (CRA) method.

A Illustration of the CRA formation by aligning the isohytes between observed (MRMS) and forecast (NowcastNet) fields, highlighting the displacement required for optimal alignment^34,35. B Spatial distributions of observed and forecasted precipitation at various lead times (T + 1 h, T + 2 h, and T + 3 h) with identified pattern and displacement errors. C Error decomposition into volume, displacement, and pattern errors for different lead times, quantified as RMSE in mm/h. D Summary of CRA verification metrics (with threshold of 16 mm/h), including Pearson correlation coefficients (CC), RMSE values, and error decomposition percentages, across different lead times, demonstrating the dominance of pattern errors in forecast accuracy.

Panel A shows the overlapping contours of observed and forecast precipitation patterns, highlighting the spatial mismatch between them. The displacement required for optimal alignment of the forecast with the observed precipitation is represented by the arrow, demonstrating how the CRA method separates errors due to incorrect location. Panel B displays the spatial distributions of observed and forecasted precipitation at three different lead times: 1 h, 2 h, and 3 h. Panel C presents the error decomposition for different lead times (10 min, 1 h, 2 h, and 3 h) as Root Mean Square Error (RMSE) in mm/hr and the errors are broken down into three components: volume error, displacement error and pattern error. Panel D provides a summary of CRA verification metrics for different lead times (1 h, 2 h, and 3 h), using a verification grid of 0.01° and a CRA threshold of 16 mm/h. The results highlight that the most significant error in NowcastNet’s predictions arises from inaccuracies in the spatial distribution of precipitation, particularly as the forecast lead time increases. Even when the total volume of rainfall is accurately captured, the model frequently misaligns the forecasted precipitation objects with their observed counterparts, resulting in substantial pattern errors. The error decomposition is further analyzed for other events shown in Fig. 5, in the Supplementary Fig. S11. Findings from this analysis show that pattern errors consistently dominate across all four events analyzed (65%–90% of the total error), with displacement errors being less prominent (10%–30% of the total error) and volume errors minimal (0–3%). However, the model’s difficulty in capturing the precise spatial structure of rainfall suggests a need for improvement in representing complex precipitation patterns.

Discussion

Precipitation nowcasting stands as a paramount objective in meteorological science, crucial for informing weather-dependent policymaking. Despite advancements, current numerical weather-prediction systems struggle to provide accurate nowcasts, particularly for extreme precipitation events^17,18. In this study, we assessed the efficacy of cutting-edge precipitation nowcasting methodologies, focusing on NowcastNet (a physics conditioned deep generative model) within the TVA service area during extreme precipitation events.

NowcastNet’s performance was compared against MRMS QPE and HRRR as well as against baseline approaches such as persistence and advection, using various skill score-based metrics such as POD, FAR, CSI, FSS, F1 Score, ETS, and HSS, as well as error- and correlation-based metrics such as RMSE, Numerical Bias, Inverse NMSE, Normalized Error, and Pearson’s Correlation. The suite of metrics, co-developed with river managers, goes beyond standard skill metrics typically used to evaluate weather forecasts. It incorporates hydrologically relevant metrics that account for extreme precipitation events, the time series of precipitation, and multiple resolutions in both time and space. Moreover, these metrics were not only essential for evaluating the model’s predictive accuracy, but also critical in assessing its operational utility in life-saving applications like river management. We focused on the Waverly event, which highlighted the challenges of predicting extreme precipitation from mesoscale convective systems. In this event, NowcastNet outperformed HRRR by accurately forecasting hotspots of extreme precipitation over 30 mm/h and predicting the trajectory of convective storms over 3-h lead times. Also, NowcastNet maintained detailed predictions across most spatial scales, with its spatial power spectral density (PSD) closely matching observed data. Furthermore, when evaluated across multiple initialization times, NowcastNet consistently followed the observed precipitation trend with minimal bias, while the HRRR model underestimated precipitation throughout the event, reinforcing NowcastNet’s robustness in handling complex weather patterns and maintaining accuracy over extended periods. In a comprehensive evaluation of 30 heavy precipitation events from 2021 to 2024, NowcastNet consistently showed higher similarity to observed MRMS data compared to HRRR and other benchmarks like persistence and advection, which struggled with fine details and intensity predictions.

In terms of skill score and correlation based metrics, NowcastNet’s better performance was noticeable against HRRR and other baseline approaches at all lead times and for all thresholds, especially at prediction of extreme precipitation at threshold >32 mm/h. In terms of error based metrics also, NowcastNet is highly effective for 1-h predictions, but it may sacrifice some accuracy in 3-h forecasts compared to HRRR which was evident from the results of RMSE, Inverse NMSE, and Normalized Error. The reason behind this is the overestimation of precipitation in longer lead times. Through the comparison of pixel-based precipitation predictions from the model, areas of both underestimation and overestimation were showcased, the consequences of which are noteworthy. Underestimation can lead to inadequate preparedness and response measures, increasing the risk of property damage, flooding, and even loss of life during extreme events. Conversely, overestimation can result in unnecessary disruptions and resource allocation, leading to economic losses and public inconvenience. Therefore, minimizing both underestimation and overestimation is crucial for improving forecast accuracy and enhancing the effectiveness of early warning systems. Notably, NowcastNet’s underestimation and overestimation tendencies intensified with longer lead times. The overestimation and underestimation of precipitation in NowcastNet primarily stem from errors in capturing the spatial patterns of rainfall, rather than inaccuracies in the total volume or displacement of precipitation. The model generally maintains an accurate total rainfall volume, demonstrating the effectiveness of the mass balance component incorporated through the continuity equation. Although displacement errors are somewhat variable, they account for only about 30% of the total error, suggesting that the model can adequately capture the spatio-temporal movement of precipitation. However, as displacement occurs, the rainfall area is expected to evolve (either grow or decay), and the model struggles to accurately represent these dynamic changes in precipitation patterns. Future efforts could improve performance by incorporating features that better capture spatial variability, or by refining the model architecture to enhance its ability to learn spatial dependencies. In summary, NowcastNet exhibited shortcomings, such as inaccuracies in estimating total rainfall and spatial imprecision at higher resolutions, underscoring the need for continued model refinement. However, it consistently outperformed HRRR and other models in predicting heavy precipitation events, and enhanced trust in DGM at 1 h lead time.

A salient feature of this study has been the co-evaluation of our nowcasting approach within our team of coauthors consisting of ML developers, hydrologists, water resources engineers and scientists, as well as river managers and hydrometeorologists working at the TVA. The TVA originally discontinued the operational use of HRRR at the request of the river forecast center’s (RFC’s) lead engineers because it was adding noise in the early lead times and was inconsistent from run to run. However, they continued examining HRRR predictions as a reference. Although HRRR is the state-of-the-art NWP model, its inability to predict extreme rainfall amounts during disastrous flooding events in the TVA region, such as the Waverly event³⁶, further reinforced their decision to discontinue the operational use of HRRR. A false sense of complacency based on missed predictions of extreme precipitation events, as seemed apparent with HRRR, could lead to inadequate guidance to flooding emergency managers and RFC operators. However, the TVA has remained interested in exploring alternatives for improved nowcasting. Our approach directly addresses this need by building trustworthiness in precipitation forecasts using physics-embedded DGM for river managers, which is a critical component for effective hazard management³⁷. Based on the results reported here, the physics-embedded ML system, specifically our implementation of NowcastNet, will be evaluated within the operational system of the TVA.

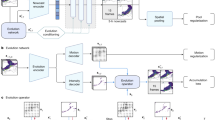
Our research highlights the critical need for further investigations to advance the accuracy of precipitation forecasting. For the longest time, it has been argued that no method has consistently outperformed Lagrangian persistence (i.e., advection or its variant, optical flow) in improving QPF at scales useful for hydrologic applications, especially for very short lead times (e.g., 1–2 h)^23,38,39. But recently deep learning methods have shown promise, compared to baseline methods, in nowcasting at shorter lead times. However, a common challenge across deep learning based nowcasting is the loss of information content as forecast lead time increases from 1 to 3 h. On the other hand, while our understanding of the physics behind precipitation, including stratiform and convective rains, continues to advance, translating this knowledge into improved prediction skills, especially at the nowcasting scale, remains challenging. So we hypothesize that by integrating additional physical principles, like momentum conservation, and incorporating diverse ancillary data sources—such as satellite observations, numerical weather predictions, surface observations, land use details, terrain characteristics, and elevation—forecast reliability can be improved. Incorporating satellite data enhances the model’s understanding of large-scale weather patterns and atmospheric dynamics, improving its ability to capture the spatial and temporal variability of precipitation. Land use information helps account for urban effects, vegetation with high transpiration, and bodies of water that influence precipitation. Terrain properties, such as slope, aspect, and roughness, are crucial for modulating precipitation due to orographic effects and wind patterns, while elevation data refine forecasts by considering changes in atmospheric stability and moisture with altitude. Finally, combining forecasts of state variables from numerical weather predictions with deep generative nowcasts could further improve accuracy. Figure 7 illustrates the evolution of precipitation forecasting methodologies, showcasing the reduction of information content in forecasts with increasing lead time and highlights the potential of physics-conditioned deep generative models to enhance forecast accuracy through multi source integration and predictive analytics.

Fig. 7: Multisource integration and predictive analytics in precipitation forecasting.

A demonstrates the reduction of prediction skill or information content of precipitation forecasts as lead time (shown in logarithmic scale) increases, comparing (a) persistence, (b) nowcasting, (c) mesoscale and (d) synoptic scale numerical weather prediction (NWP), (e) merged approach within the boundary of (f) limit of predictability^44,63,64,65. Merged forecasts can be a combination of nowcasting, NWP models, satellite information, etc. B demonstrates generation of precipitation forecasts using a deep generative model (DGM). The proposed DGM combines observed remotely sensed data from radar and geostationary satellites, ground sensors, ancillary information from terrain properties, physics of precipitation^22,66 and NWP state variables to enhance forecast accuracy.

Most of this study’s analysis has been done at the grid cell level, but basin-level analysis is important for river management and flood management. The fact that this study reported most metrics at the grid cell level means there has not been quantification of how far away hotspots are when they are wrongly placed—an observed hotspot 2 km away from the forecasted hotspot is much better than 10 km away, so more evaluation is required to understand this. A precipitation hotspot misplaced across basin lines may demand emergency preparations in a completely different river, whereas a precipitation hotspot misplaced within the same basin requires much the same preparations. Geographically incorrect hotspots were a major problem with HRRR, prompting its discontinuation in TVA’s decision-making, so basin-wise or dam-wise evaluation of NowcastNet would quantify the confidence that NowcastNet could serve a similar role in hourly-level flood management without the geographic errors.

In conclusion, advancing precipitation nowcasting is crucial for informed decision-making in meteorology, especially for extreme events. While methodologies like NowcastNet show promise in capturing convective events, they exhibit limitations such as false alarms and spatial imprecision. Further model refinement and integration of diverse data sources offer avenues for improvement.

Methods

Nowcasting methods

In this section, we outline the mathematical formulations of various nowcasting techniques, starting with the foundational method of Persistence and progressing through Optical Flow analysis, Numerical Weather Prediction (NWP) models, Machine Learning (ML) techniques, physics-free approaches, and finally physics-conditioned Deep Generative Models.

Persistence-based nowcasting in atmospheric science involves incorporating knowledge of precipitation physics into simple models. Traditional approaches include climatological precipitation history, Eulerian persistence, Lagrangian persistence, and persistence of convective cells³⁹. Eulerian persistence (Eq. (1)) predicts future observations based on the most recent observation, while Lagrangian persistence (Eq. (2)) accounts for the displacement of air parcels. The Lagrangian persistence assumption is particularly relevant for short-term rainfall prediction and forms the basis of current radar extrapolation models⁴⁰.

The Eulerian persistence model represents the forecasted precipitation field $(\hat{\psi })$ at a future time (t₀ + τ) as equal to the observed precipitation field (ψ) at the initial time (t₀), without considering any displacement. In contrast, the Lagrangian persistence model incorporates a displacement vector (λ) into the equation, representing the movement of air parcels. It forecasts the precipitation field $(\hat{\psi })$ at a future time (t₀ + τ) by shifting the observed precipitation field (ψ) at the initial time (t₀) by the displacement vector (λ):

$$\hat{\psi }({t}_{0}+\tau ,x)=\psi ({t}_{0},x)$$

(1)

$$\hat{\psi }({t}_{0}+\tau ,x)=\psi ({t}_{0},x-\lambda )$$

(2)

Optical flow techniques, essential in precipitation nowcasting, infer motion patterns from consecutive image frames^21,41. These methods operate at both local and global scales, utilizing optical flow constraints (OFCs) to delineate motion in specific areas or across entire images^41,42,43. Equation (3) describes the Optical Flow Constraint (OFC) equation, which assumes that features within an image sequence maintain their size and intensity while changing shape, serving as the foundation for subsequent models such as STEPS²¹:

$$\frac{\delta R}{\delta t}+u\frac{\delta R}{\delta x}+v\frac{\delta R}{\delta y}=0$$

(3)

In Eq. (3), the terms (u,v) represent the velocity field, while R(x,y) denotes the rain rate at the coordinate (x,y). The rain rate R is known at each point, and a sequence of images helps estimate the partial derivatives required in Eq. (3).

NWP models have improved precipitation forecasting through statistical interpretation, which involves analyzing historical weather data to identify patterns and relationships between various atmospheric variables. However, NWPs only explicitly capture broader weather patterns. So, they are most effective for generating general forecasts 12 h ahead and beyond⁴⁴. HRRR is an NWP model that played a pivotal role in providing convective storm guidance, over the past decade^25,26,45. However, with advancements in technology and modeling techniques, the HRRR is transitioning to the Finite Volume Cubed (FV3)-based Rapid Refresh Forecast System (RRFS)⁴⁶. The RRFS represents an evolution from the HRRR, incorporating improvements in resolution, physics parameterizations, and data assimilation techniques^45,47.

In recent years, machine learning has emerged as a promising tool for precipitation nowcasting, offering solutions to limitations in traditional methods like optical flow and numerical weather prediction models (NWPs)⁴⁰. Optical flow methods face challenges due to assumptions of Lagrangian persistence and smooth motion fields, while NWPs struggle to capture fine-scale spatio-temporal patterns associated with convective storms. Machine learning offers potential solutions by capturing complex spatio-temporal patterns, integrating diverse data sources, and introducing approaches like spatiotemporal convolution^16,20,22, adversarial training^23,24,48, and latent random variables⁴⁹ to enhance nowcasting capabilities. Among these, the state-of-the-art physics-free deep generative model is DGMR by Google DeepMind²³.

Equation (4) describes the nowcasting methodology of the DGMR model which relies on a conditional generative approach to predict N future radar fields based on past M observations²³. This model incorporates latent random vectors Z and parameters θ, ensuring spatially dependent predictions by integrating over latent variables²³. The learning process adopts a conditional generative adversarial network (GAN) framework, tailored specifically for precipitation prediction. Specifically, the model utilizes four consecutive radar observations spanning the previous 20 min as contextual input for a generator which enables the generation of multiple future precipitation scenarios over the next 90 min²³:

$$P({X}_{M+1:M+N}| {X}_{1:M})=\int\,P({X}_{M+1:M+N}| Z,{X}_{1:M},\theta )P(Z| {X}_{1:M})dZ$$

(4)

Although DGMR generates predictions which are spatio-temporally consistent with ground truth for light to medium precipitation events, it produces nowcasts with unnatural motion and intensity, high location error, and large cloud dissipation at increasing lead times²⁴. So, in this study, we focus on the state-of-the-art physics conditioned deep generative model NowcastNet²⁴. This model employs a physics-conditional deep generative architecture to forecast future radar fields based on past observations, as described in Eq. (5)²⁴. It consists of a stochastic generative network parameterized by θ and a deterministic evolution network parameterized by ϕ, allowing for physics-driven generation from latent vectors z²⁴:

$$P({\hat{X}}_{1:T}| {X}_{-{T}_{0}:O},\phi ;\theta )=\,\int\,P({\hat{X}}_{1:T}| {X}_{-{T}_{0}:O},\phi ({X}_{-{T}_{0}:O}),Z;\theta )P(Z)dZ$$

(5)

This integration enables ensemble forecasting, capturing chaotic dynamics effectively and ensuring physically plausible predictions at both mesoscale and convective scales. The modified 2D continuity equation for precipitation evolution²⁴, can be represented as:

$$\frac{\delta x}{\delta t}+(\vartheta .\nabla )=s$$

(6)

In this equation, x, ϑ, and s represent radar data pertaining to composite reflectivity, motion fields, and intensity residual fields, respectively. The symbol ∇ denotes the gradient operator. This equation represents the conservation of mass for precipitation fields over time and space. In simpler terms, it describes how precipitation changes and moves within a given area, considering factors like radar reflectivity, motion fields (velocity of precipitation movement), and intensity residual fields (changes in precipitation intensity). NowcastNet adaptively combines mesoscale patterns governed by physical laws with convective-scale details from radar observations, resulting in skillful multiscale predictions with up to a 3-h lead time²⁴. More information is provided in Supplementary Information Section B.

Evaluation metrics

Evaluation metrics serve as crucial tools for assessing NowcastNet’s performance in generating precipitation nowcasts. Murphy described three pillars of forecast evaluation⁵⁰. Firstly, consistency, which refers to the harmony between forecasters’ judgments and the forecasts they generate. Secondly, quality, which assesses the concordance between the forecasts and the corresponding observations. Lastly, goodness, which can be thought of as value, evaluates the incremental economic or other benefits realized by decision-makers through the application of the forecasts⁵⁰. We employed a set of metrics to evaluate the performance of NowcastNet and HRRR with respect to MRMS. These metrics include categorical skill scores: Probability of Detection (POD), False Alarm Ratio (FAR), Critical Success Index (CSI), F1 Score, Equitable Threat Score (ETS), Heidke Skill Score (HSS) and the Fractions Skill Score (FSS) which is neighborhood-based. We estimated PSD for frequency analysis. We also employed error and correlation based metrics which include Root Mean Squared Error (RMSE), Numerical Bias, Inverse NMSE, Normalized Spatially Averaged Error, and Pearson Correlation. Lastly, we employed the Contiguous Rainfall Area (CRA) method for error decomposition into volume, displacement and pattern error.

The categorical scores are derived from the 2 × 2 contingency table (Table 1), also known as a confusion matrix, clarifying which pixels were observed as events in MRMS and which pixels were forecast as events by the model. Common nomenclature refers to a as Hits, b as False Alarms, c as Misses, and d as Correct Negatives, Correct Nonevents, or Correct Rejections.

Table 1 Contingency metrics

The probability of detection (POD) measures the fraction of observed events correctly predicted by the model (Eq. (7)) and the false alarm ratio (FAR) quantifies the ratio of false alarms to the total number of forecasted events (Eq. (8)):

$$POD=\frac{a}{a+c}$$

(7)

$$FAR=\frac{b}{a+b}$$

(8)

The Critical Success Index (CSI)⁵¹ assesses binary forecasts, determining whether rainfall surpasses a specified threshold t. It provides a comprehensive evaluation of binary classification performance, accounting for both false alarms and misses, and is widely used in the forecasting domain. The CSI measures the ratio of correctly predicted events to the total number of observed and forecasted events (Eq. (9)):

$$CSI=\frac{a}{a+b+c}$$

(9)

CSI is prone to bias because it tends to yield lower scores for rare events^52,53. To counteract this bias, another scoring method can be utilized to adjust for hits expected by chance. This method is known as the equitable threat score (ETS) or the Gilbert skill score⁵⁴. The Equitable Threat Score (ETS) spans from −1/3 to 1. When the score falls below 0, it indicates that the chance forecast is favored over the actual forecast, suggesting the forecast lacks skill. ETS is calculated using the formula:

$$\,{\text{ETS}}\,=\frac{(a-{a}_{r})}{(a+b+c-{a}_{r})},\quad \,{\text{where}}\,\quad {a}_{r}=\frac{(a+b)(a+c)}{a+b+c+d}$$

(10)

The Heidke skill score (HSS) was originally introduced by Heidke in 1926⁵⁵. It serves as a skill score for categorical forecasts. It is based on the proportion of correct predictions (both Hits and Correct Negatives) but scales according to correct predictions attributable to chance⁵⁶:

$$\,{\text{HSS}}\,=\frac{2(ad-bc)}{(a+b)(a+c)+(c+d)(b+d)}$$

(11)

This way, HSS ranges from negative infinity to 1. Negative values indicate that the chance forecast outperforms the actual forecast, while 0 indicates no skill, just as good as chance. A perfect forecast achieves an HSS of 1.

The F1 score combines precision and recall, providing a balance between them. Here, precision measures the fraction of predicted events for which the prediction was correct, indicating how correct the model was when it predicted positive cases. Precision is equivalent to 1 − FAR, so a higher precision means lower false alarm ratio. On the other hand, recall, equivalent to the POD, assesses the fraction of positive cases that were correctly identified by the classifier, indicating how correct the model was when an event (positive) was observed. F1 score (Eq. (12)) is calculated as the harmonic mean of precision and recall (with a threshold of 0.1 mm/h, 16 mm/h and 32 mm/h, for differentiating precipitation events and non-events), indicating the model’s accuracy both relative to its own predictions and relative to observed events:

$$F1\,{{Score}}=2\,\frac{{{Precision}}\times {{Recall}}}{({{Precision}}+{{Recall}})}$$

(12)

Where, ${{Recall}}={{POD}}=\frac{a}{a+c}$ and ${{Precision}}=\frac{a}{a+b}=1-{{FAR}}$

The fractions skill score (FSS) is a commonly used neighborhood verification method designed to mitigate displacement errors by comparing neighborhood fractions for both forecast and observed fields at various spatial scales⁵⁷. Forecasts often face verification challenges due to double-penalty errors from small-scale displacement³³. Traditional grid-point verification can be misleading, so neighborhood approaches help address these issues, improving accuracy across applications:

$${\rm{FSS}}=1-\frac{\mathop{\sum }\nolimits_{i=1}^{I}{\left({{\rm{NP}}}_{i,{\rm{f}}}-{{\rm{NP}}}_{i,{\rm{o}}}\right)}^{2}}{\mathop{\sum }\nolimits_{i=1}^{I}{{\rm{NP}}}_{i,{\rm{f}}}^{2}+\mathop{\sum }\nolimits_{i=1}^{I}{{\rm{NP}}}_{i,{\rm{o}}}^{2}}$$

(13)

where NP_i,f is the neighborhood fraction for the forecast at grid point i. NP_i,o is the neighborhood fraction for the observation at grid point i. I is the total number of grid points considered in the domain. In this study, neighborhood sizes of 1 to 27 are used. For 1 km spatial resolution, a neighborhood size of 3 means a 3 × 3 grid area or 3 km area centered around the target grid point. For 3 km spatial resolution, a neighborhood size of 3 means a 3 × 3 grid area or 9 km area centered around the target grid point. The analysis is conducted for all three precipitation thresholds: >0.1 mm/h, >16 mm/h, and >32 mm/h.

The RMSE measures the standard deviation of the residuals or the prediction errors. A low RMSE denotes less difference between the observed and predicted values of the variable of interest. RMSE has the same units as the variable:

$${RMSE}=\sqrt{\frac{1}{n}\mathop{\sum }\limits_{i=1}^{n}{({x}_{i}-{y}_{i})}^{2}}$$

(14)

Here, n = number of lead times, x_i = observed mean precipitation and y_i = predicted mean precipitation.

The numerical bias of the forecasts is defined as the ratio of the mean forecast value to the mean observed value across all pixels. A bias value closer to 1 indicates less bias and more accurate forecasts, while values significantly higher or lower than 1 indicate greater bias and less accurate forecasts. Bias higher than 1 means the forecast overestimates observed MRMS precipitation, and bias less than 1 means the forecast underestimates observed MRMS precipitation:

$${{Bias}}=\frac{{{Mean}}\,{{Forecast}}\,{{Value}}}{{{Mean}}\,{{Observed}}\,{{Value}}}$$

(15)

The normalized spatially averaged error, or normalized root mean square error, measures the average prediction error as proportion of the spatial mean precipitation. Higher errors indicate lower forecast skill:

$${{Normalized}}\,{{Error}}=\frac{{{RMSE}}}{{{Mean}}\,{{Observed}}\,{{Value}}}$$

(16)

The inverse of the normalized root mean square errors (Inverse NMSE) measures how well the forecast captures the spread of observed pixel values. It is calculated for pixels with nonzero rainfall. A perfect forecast results in Inverse NMSE approaching infinity. For a stationary process, Inverse NMSE equal to 1 indicates that the RMSE equals the standard deviation of the observed pixels, therefore the forecast is as good as predicting the spatial mean in every location. Inverse NMSE less than 1 means the forecast captures the spread worse than a spatial mean prediction:

$${{Inverse}}\,{{NMSE}}=\frac{{{Standard}}\,{{Deviation}}\,{{of}}\,{{Observed}}\,{{Data}}}{{{RMSE}}}$$

(17)

Pearson’s correlation (Eq. (18)) assesses the similarity between spatial patterns of observed and forecasted precipitation fields:

$${{Correlation}}=\frac{\mathop{\sum }\nolimits_{i = 1}^{n}({x}_{i}-\bar{x})({y}_{i}-\bar{y})}{\sqrt{\mathop{\sum }\nolimits_{i = 1}^{n}{({x}_{i}-\bar{x})}^{2}\mathop{\sum }\nolimits_{i = 1}^{n}{({y}_{i}-\bar{y})}^{2}}}$$

(18)

Where, n = number of grid cells, x_i = observed precipitation, y_i = predicted precipitation $\bar{x}$ = mean observed precipitation and $\bar{y}$ = mean predicted precipitation.

The spatial power spectral density (PSD)^58,59 characterizes the distribution of precipitation intensities using Fourier transform techniques (Eq. (19)). This captures the information content—here variance of rain rate—at different spatial scales. Forecasts whose information content matches observations’, at all spatial scales, are more desirable. Power spectral density is a function of wavelength. To compute PSD across the geography of interest, first the Fourier transform is computed in each dimension. The Fourier transform has information about different wavelengths, so bins of wavelengths are created and in each bin, the variance of amplitude of the Fourier signal is taken. Below is the formula⁵⁹ for the Fourier transform in one dimension. F(x_j) is the Fourier approximation of the signal y_j at each of the n grid cells x_j. L is the length (e.g., in kilometers) of the dataset in this dimension. The values of k from 1 through m are the different wavelengths considered. Then, a₀, a_k, b_k are the Euler-Fourier coefficients that define the signal:

$$F({x}_{j})=\frac{{a}_{0}}{2}+\mathop{\sum }\limits_{k=1}^{m}{a}_{k}{{cos}}\left(2\pi k\frac{{x}_{j}}{L}\right)+{b}_{k}{{sin}}\left(2\pi k\frac{{x}_{j}}{L}\right)$$

(19)

The Contiguous Rainfall Area (CRA) method is the first feature-based approach developed to evaluate systematic errors in rain system predictions by decomposing total error into components related to location, amplitude, and fine-scale pattern differences^34,35,60. In the CRA method, a rain entity is defined using an isohyet (rain rate contour), and the forecast entity is translated and rotated over the observed entity until the best fit is achieved based on criteria like minimum squared error, maximum correlation, or maximum overlap^60,61. The displacement vector provides the location error. The forecast’s mean squared error (MSE) is then decomposed into displacement, volume, and pattern errors:

$${\text{MSE}}_{{\rm{total}}}={\text{MSE}}_{{\rm{displacement}}}+{\text{MSE}}_{{\rm{volume}}}+{\text{MSE}}_{{\rm{pattern}}}.$$

(20)

The error decomposition based on correlation optimization is:

$${\text{MSE}}_{{\rm{total}}}={(F-X)}^{2}+{({\sigma }_{X}-r{\sigma }_{F})}^{2}+(1-{r}^{2}){\sigma }_{F}^{2},$$

(21)

where F and X are the mean forecast and observed values before the shift; σ_F and σ_X are the standard deviations of the forecast and observed values, respectively; and r is the original spatial correlation between the forecast and observed features. Correcting the forecast location improves its correlation with the observations, r_opt. Adding and subtracting r_opt and rearranging:

$${\text{MSE}}_{{\rm{displacement}}}=2{\sigma }_{F}{\sigma }_{X}({r}_{{\rm{opt}}}-r),$$

(22)

$${\text{MSE}}_{{\rm{volume}}}={(F^{\prime} -X^{\prime} )}^{2},$$

(23)

$${\text{MSE}}_{{\rm{pattern}}}=2{\sigma }_{F}{\sigma }_{X}(1-{r}_{{\rm{opt}}})+{({\sigma }_{F}-{\sigma }_{X})}^{2}.$$

(24)

In this study, we have estimated the best fit based on maximum correlation and a rain threshold of 16 mm/h is used to define the CRA to focus on extreme rainfall. We also take the square root of each component to report an RMSE, which has more easily interpretable units.