Preserving information while respecting privacy through an information theoretic framework for synthetic health data generation

Abstract

Generating synthetic data from medical records is a complex task intensified by patient privacy concerns. In recent years, multiple approaches have been reported for the generation of synthetic data, however, limited attention was given to jointly evaluate the quality and the privacy of the generated data. The quality and privacy of synthetic data stem from multivariate associations across variables, which cannot be assessed by comparing univariate distributions with the original data. Here, we introduce a novel algorithm (MIIC-SDG) for generating synthetic data from electronic records based on a multivariate information framework and Bayesian network theory. We also propose a new metric to quantitatively assess the trade-off between the Quality and Privacy Scores (QPS) of synthetic data generation methods. The performance of MIIC-SDG is demonstrated on different clinical datasets and favorably compares with state-of-the-art synthetic data generation methods, based on the QPS trade-off between several quality and privacy metrics.

Introduction

With the significant increase in patient recruitment for clinical trials and the collection of real-life health-related datasets over the past few decades, ensuring patient privacy has become of utmost importance. Indeed, facilitating new research initiatives and promoting data sharing are necessary for pushing the boundaries of biomedical research. Machine learning and deep learning approaches offer promise in synthesizing health data while safeguarding patient privacy. However, existing regulatory standards, including the European General Directive on Data Protection (GDPR), often impose restrictions on data sharing and secondary data usage due to concerns about data security.

The primary and secondary use of sensitive data must not only comply with local legislations, but also align with the initial patient consent to safeguard personal privacy. Data publication needs to guarantee Statistical Disclosure Control (SDC), referring to techniques able to ensure that no person is identifiable from the published data. This includes two possible cases: (i) identification disclosure when an attacker is able to link some data to a specific individual and (ii) attribute disclosure when the attacker is able to learn new information on the subject, by using prior knowledge and the information contained in the data.

Classical anonymization techniques like k-anonymity, first introduced by Latanya Sweeney and Pierangela Samarati¹ in 1998, protect user data by minimizing the risk of re-identification, while keeping in theory a good level of data utility. K-anonymity is obtained through data suppression and data generalization, so that each person in the collection cannot be distinguished from at least k-1 individuals by using quasi-identifier features (attributes available to an adversary). Machanavajjhala and colleagues showed k-anonymity to be vulnerable to some attacks when using background knowledge² and proposed a new privacy criteria, named l-diversity. In 2007, Li and colleagues published a novel privacy criteria named t-Closeness, with even stronger properties for privacy preservation³. In addition to being computationally expensive⁴ and requiring prior knowledge to be able to anonymize the data, these classical tools are shown to deteriorate the data distribution, making them no longer exploitable in many situations.

Together with traditional anonymization techniques, recent technological advances in artificial intelligence, notably in generative modeling, led to the development of synthetic tabular data generation (SDG) algorithms⁴. SDG is performed by training a machine learning model on a real data set to generate synthetic data that mimic the original dataset. This process is done by learning the underlying data distribution and using it to generate synthetic samples. A vast number of methods have been developed over the last decade for synthetic tabular data generation⁴. Among the algorithms that can deal with mixed type data, combining categorical, discrete and continuous variables, are Classification and Regression Trees (CARTs), Bayesian Networks⁵ and Variational Autoencoders (VAE).

In addition, recent advancements in Deep Learning have led to the emergence of a new category of methods known as Generative AI. This field encompasses various techniques, including Generative Adversarial Networks (GANs) and Diffusion-based models. Initially developed for generating high-quality images, significant progress has been made to apply these methods to tabular data, particularly Electronic Health Records (EHRs), which offer a vast amount of data for training such models.

Notably, there are Wasserstein-GAN models, such as EMR-WGAN⁶ and medWGAN⁷ (derived from medGAN⁸ model), that are specifically designed for generating high-quality samples from electronic medical records. More recently, diffusion-based models like EHRDiff⁹ and MedDiff¹⁰ have also been adapted to generate synthetic health data, similar to the work done with GAN models.

A recent review⁴ reported multiple methods for tabular data generation with a focus on the healthcare application context showing that there is no universal method or metric to evaluate and benchmark the performance of various approaches, both in terms of quality and privacy preservation. Several algorithms^11,12 have been reported to generate high fidelity data while showing an optimal level of privacy but looking at data quality primarily through the prism of similarity of univariate distributions between the synthetic and original data. However, the richness of information in a dataset stems from the intricate multivariate associations among variables. These associations also contribute to privacy concerns, as combinations of quantitative variables can potentially be exploited to re-identify individuals. Therefore, it is crucial to consider the trade-off between data quality and data privacy when evaluating synthetic data generation methods, particularly in the context of clinical trials for which the number of patients and controls are typically limited.

As synthetic data generation algorithms do not create anonymized versions of the original samples but rather generate entirely new data that capture the statistical properties of the original dataset, metrics suited to traditional anonymization, like k-anonymity, are therefore not applicable in this context. We thus chose to use other relevant metrics, adapted from the identifiability and the membership inference scores, to assess the effectiveness in preserving the privacy of the original data.

The evaluation of data quality in synthetic tabular datasets, highlighted in a recent survey¹³, emphasizes the significance of metrics such as inter-dimensional relationship similarity, latent distribution similarity, joint distribution similarity, and prediction similarity. Recognizing the importance of capturing these aspects comprehensively, our benchmarks incorporate different metrics across a range of variable scales. At univariate scale, we perform chi-square and Wilcoxon tests. We then consider metrics in the bivariate context, using correlation and mutual information, and metrics in the multivariate context, with Wasserstein distance, to thoroughly assess the quality of synthetic datasets.

The existence of a privacy-utility trade-off in synthetic data has already been recognized and investigated¹⁴. We quantify this trade-off in our benchmarking by introducing a Quality-Privacy Score (QPS) which combines different quality and privacy metrics to evaluate synthetic health data.

This paper serves two purposes: First, we propose a novel synthetic tabular data generation algorithm specifically suited for health records. It is based on the results of the Multivariate Information-based Inductive Causation (MIIC) algorithm^15,16 that has been shown to reliably capture multivariate relations across features. Second, we use multiple quality and privacy metrics and introduce a trade-off measure between these two complementary metrics, with the aim of comparing state-of-the-art synthetic healthcare data generation algorithms.

Methods

In this section we first describe our novel synthetic data generation method: the MIIC-SDG algorithm is able to generate synthetic data that accurately captures the underlying multivariate distribution of the original data, without duplicating the data. The method is based on the reconstruction of a bayesian network that preserves direct associations and causal relationships from the original dataset. In the second part we review existing algorithms for synthetic tabular data generation and compare their performance over two real life benchmark datasets. Finally, we discuss metrics for evaluating quality and privacy of synthetic data, individually and jointly.

The proposed method, MIIC-SDG, takes advantage of the MIIC algorithm^15,16,17,18 (MIIC network reconstruction) which can reliably capture the set of direct associations in complex heterogeneous datasets such as healthcare medical records. MIIC-SDG expands on the MIIC algorithm by adding a new algorithm that transforms a graph into a directed acyclic graph (MIIC-to-DAG) as well as a synthesizer (MIIC synthesizer) that takes into account the joint multivariate distribution associated with the data to generate high-quality samples that mimic the original data.

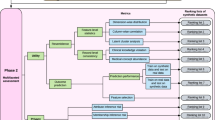
MIIC-SDG algorithm is composed of three steps, as shown in Fig. 1:

• A. MIIC: Inferring a graphical model associated with the original dataset using MIIC algorithm.

• B. MIIC-to-DAG: Creating a directed acyclic graph (DAG) using the previously inferred network.

• C. MIIC-synthetizer: Generating synthetic samples based on the DAG and the original data by using several approaches that depend on the nature of parents and children nodes in the graph.

Fig. 1: MIIC-SDG pipeline.

This illustration shows the complete data generation process, from the original data table to the generated data, following the 3 main steps described in section “MIIC network reconstruction” of Methods. a Execution of the MIIC algorithm from the original data table. This step generates a graph where nodes represent the variables of the data matrix and edges represent direct associations between variables. b Transformation of the graph into a directed acyclic graph (DAG) through the MIIC-to-DAG algorithm. c Generation of the data using the original data table and the reconstructed DAG. d Details on the data generation step: each scenario takes into account the variable type of the target and parents nodes to adapt the sampling procedure (branches (a–f) are described in the section “MIIC-synthetizer” of Methods. RF: Random Forest; Cond. Prob. Table: Conditional Probability Table; Prob. Table: Probability Table; Emp. Dens.: Empirical density).

The MIIC-SDG algorithm is available as an R package, allowing the user to create synthetic versions of the original data inside a secured environment, without requiring any personal data to be transmitted to a web-server.

MIIC network reconstruction

The MIIC (Multivariate Information-based Inductive Causation) is an algorithm that infers a graphical network to represent the direct and possibly causal associations between variables in a dataset^15,16. The algorithm has the ability to estimate conditional mutual information, even when the dataset includes a mixture of categorical and continuous variables. MIIC does not have hyperparameters and is not sensible to the order of features in the input data. It can estimate the set of associations between variables in the presence of missing data without the need of an a priori data imputation technique. MIIC has proven to be robust to sampling noise and to reliably estimate (conditional) mutual information. These features have been demonstrated in multiple benchmarks^16,19.

The MIIC-generated graph is composed of both directed and undirected edges, and may contain directed cycles, a common characteristic of causal discovery constraint-based methods. The directed edges result from identifying v-structures¹⁵ (A → B ← C), where two independent and thus unconnected variables are linked to a third one. Additionally, directed edges can result from the propagation of orientations from upstream v-structures. However, propagated orientations do not necessarily indicate causal associations.

MIIC is available through a web-server¹⁸ and an R package and has been recently applied to a breast cancer cohort of 1200 patients treated at Institut Curie, Paris¹⁷, as well as a larger cohort of 400,000 breast cancer patients from the SEER database^16,19. MIIC provides a novel way to globally visualize, analyze, and understand the connections between well-known clinical features.

MIIC DAG generation

In this study, we expand MIIC’s ability to learn unparameterized network structures by incorporating a framework capable of generating synthetic data from a MIIC reconstructed graph. This approach takes advantage of the Bayesian framework, where the starting point is a DAG that can be parametrized using the original data. In this scenario, prior to data generation, the initial graph has to be transformed into a DAG. To this end, we designed and implemented a new algorithm, MIIC-to-DAG, that orients all undirected edges and removes all directed cycles from the original graph reconstructed by MIIC, while retaining most v-structures and propagated orientations from the original MIIC network, whenever possible. This limits the impact of MIIC-to-DAG on the causal relationships and/or associations found from the real data. In particular, the propagation of orientations used by MIIC ensures that all remaining undirected edges in the MIIC structure can be oriented in either direction without adding new v-structures in the MIIC-DAG, unless such orientations create cycles. Indeed, orientating these undirected edges does not change the actual associations between the implicated variables, despite changing their causal relations, due to global Markov equivalence between the corresponding graphs.

MIIC-to-DAG algorithm consists in two steps: first, we orient each undirected edge in the MIIC network so as to minimize the number of directed cycles and possibly avoid them. Then, we remove all directed cycles from the graph, if some are present. In order to guarantee the removal of all the cycles of the graph, MIIC-to-DAG iteratively considers the longest cycle in the graph (the one with the most edges) and flips the edge that minimizes the number of remaining cycles in the graph. Taking the longest cycle guarantees the removal of at least one cycle at each iteration and therefore convergence towards a DAG. The pseudocode of the MIIC-to-DAG procedure is presented in Supplementary Fig. 9. Beyond the visualization of the MIIC reconstructed network, the MIIC web server also enables the visualization of the DAG generated by the MIIC-to-DAG algorithm, by loading the list of directed edges available in the output of the execution of the MIIC-SDG algorithm. This step allows the user to inspect the DAG and to check the associations used to generate the data for each single variable. Details are present in the manual of MIIC-SDG (code availability section). The visualization of the causal network is possible at the following address: https://miic.curie.fr/vis_NL.php.

MIIC synthesizer

In this extension of the MIIC algorithm, the data generation component leverages the DAG structure obtained in the second step. The MIIC-SDG synthesizer follows the same concept of other algorithms based on Bayesian assumptions, where the sampling is initialized from variables associated with isolated or orphan nodes and then iteratively expands to nodes whose parents have already been generated. To address the presence of mixed-type variables in the original data, specific modifications have been implemented for the data generation algorithm.

There are different scenarios depending on the nature of the parent(s) (P) variable(s) and the target (T) variable:

• 1. T discrete - P discrete : this corresponds to classical Bayesian network algorithms where a multivariate conditional probability table for the target variable (child node) is estimated from the original data and then used to sample synthetic data based on parents values (branch a of Fig. 1d). When the target variable is a root node or an isolated node, the sampling is done directly from the target original probability table (branch b of Fig. 1d).

• 2. T discrete - P continuous/mixed: we implemented this scenario with two different methods (branch c of Fig. 1d). On the one hand, if the number of continuous parents is low (<3), continuous distributions are discretized using an optimum discretization algorithm from the MIIC framework¹⁶ that maximizes the mutual information between each parent and the target variable. This approach has shown to reliably estimate theoretical mutual information and to be adaptive to the number of samples and multimodal continuous distributions. We then applied the same method described in the first scenario to sample the target distribution. This method circumvents the difficulty of directly predicting a strongly unbalanced discrete variable with a classification model when the number of continuous predictors is low.

  On the other hand, when the number of continuous parents is higher (3 or more), we choose to resort to a random forest classification model to predict the target variable, as it is able to capture non-linear associations between multiple predictors without having to discretize continuous parents.

• 3. T continuous - P discrete: in this scenario we estimate the density of the continuous target for each combination of discrete parents and sample from the empirical estimated density (branch d of Fig. 1d). In case the target variable is a root node or an isolated node, the sampling is done directly on the estimated density of the original variable (branch e of Fig. 1d).

• 4. T continuous - P continuous/mixed : this case is addressed with two methods (branch f of Fig. 1d): first, if the number of continuous parents is low (<2), we use the optimum discretization algorithm from the MIIC framework and then learn and reproduce the density of the continuous target for each combination of discrete or discretized parents. If the number of continuous parents is higher (2 or more), we implement a random forest regression model to predict the continuous target node.

It is important to notice that missing values are represented as an extra category for discrete and categorical variables and hence reproduced in the synthetic generated data. For continuous variables, where densities estimation or classification/regression are applied, no missing value is generated for the synthetic feature.

Benchmark algorithms

MIIC-SDG

As detailed above, MIIC-SDG is composed of three steps: (A) discovers a network structure from the input data, (B) transforms this network into a DAG using MIIC-to-DAG algorithm and (C) uses this DAG and the original data to generate synthetic samples resembling the original data. The whole algorithm is detailed in the ‘Methods’ section “MIIC network reconstruction”.

Bayesian

This method builds a probabilistic graphical model (Bayesian network) that represents the joint multivariate distribution by exploiting dependencies between random variables²⁰. In this framework, a DAG and a corresponding conditional probability distribution are learned from the given data. Sampling from the model is finally performed to generate a synthetic dataset. We used the code provided in the Synthcity²¹ package that uses the pgmpy package by Ankur and Abinash²⁰. The DAG is obtained using the tree search (Chow–Liu tree) or hill climbing algorithms.

Synthpop

The Synthpop algorithm, developed in 2016 by Nowok and colleagues, is a machine learning solution designed to generate synthetic test data for users who work with confidential datasets²². The synthetic data, generated through parametric and nonparametric methods, including the classification and regression trees (CART) model, aims to mimic the original data and can be used for exploratory analyses and for testing models. However, the CART model may result in final leaves with a small number of individuals, potentially compromising the privacy of the synthesized data. The authors suggest limiting this effect by specifying a minimum size for the final node produced by the CART model, though determining the appropriate value for this parameter is challenging as it is data-dependent and the method does not offer a tuning procedure.

CTGAN

CTGAN (Conditional Tabular Generative Adversarial Networks) is a deep learning algorithm published by Xu and colleagues in NeurIPS 2019, that aims at creating a generative model suitable for tabular data. CTGAN differs from traditional GANs by adding a conditional structure to both the generator and the discriminator networks, allowing it to generate synthetic samples based on specific real-world conditions. Authors have reported CTGAN outperforming Bayesian methods on most of the real datasets they presented²³.

TVAE

Tabular Variational AutoEncoders are adapted from classical variational autoencoders (VAE)²³ to enable the generation of mixed-type tabular data. This method was also used as a benchmark in the CTGAN paper. Authors claim that CTGAN achieves competitive performance across many datasets and outperforms TVAE on some benchmarks.

PrivBayes

PrivBayes is a differentially private Bayesian network model capable of efficiently handling datasets with a large number of attributes²⁴. Authors present the package as a new implementation that requires the injection of less noise compared to other differential privacy algorithms, maintaining more signal in the synthetic data. To obtain differentially private synthetic data, PrivBayes starts by creating a Bayesian network that succinctly represents the correlations among the attributes and then injects noise into each marginal distribution to ensure differential privacy. The method finally uses these noisy marginals and the bayesian network to generate synthetic samples. The most important parameter for the algorithm is epsilon, determining the amount of noise injected in the marginal distributions. However, the choice of epsilon is not straightforward since the level of both quality and privacy of the generated data depends on the type of distributions, number of samples and complexity of the Bayesian network. For this benchmark, we choose an epsilon equal to 1 as it showed to be the best compromise in our simulations.

MedWGAN

medWGAN⁷ is a modified version of the medGAN model⁸. The medGAN model is a generative adversarial network for generating multi-label discrete patient records. It can generate both binary and count variables (i.e. medical codes such as diagnosis codes, medication codes or procedure codes). The modified medWGAN version introduced a Wasserstein GAN with gradient penalty as alternatives to the GAN in the medGAN framework. Among other benefits, the Wasserstein GAN offers an improved training stability by addressing mode collapse and enhanced gradient flow through techniques that stabilize and maintain a consistent gradient throughout the network. These advantages make WGAN a valuable approach in generative modeling tasks, enabling the generation of diverse and high-quality samples.

Random in range

This naive approach is used as a lower bound for normalizing the other benchmark methods. The “synthetic dataset” is obtained by generating random data using uniform distributions (inside the ranges of the original data). For categorical data it corresponds to a random sampling with replacement from all possible levels of categories of each feature. For continuous variables the sampling is made using the minimum and maximum values as ranges and sampling within the range with a uniform distribution.

In choosing these benchmark algorithms, we intentionally selected ones that employ different techniques for generating synthetic tabular data. A critical common feature among these chosen methods is their use of sampling from an estimated true joint distribution for data anonymization. This shared approach provided a foundation for comparing the performance of our method with these established benchmarks.

Algorithms parameters

To compare to other approaches, we used the default parameters further detailed in Supplementary Table 1.

During the initial step of MIIC-SDG, we employed specific parameters of the MIIC algorithm to facilitate the generation of the most oriented network. This involved enabling both orientation and propagation. We deliberately avoided the exploration of latent variables, deeming them less crucial for generating new data from the resultant network. Additionally, we opted not to implement any filtering on edge confidence, aiming to capture the most information on associated variables. Finally, KL-distance was enabled during the search for confounders in the presence of missing data, a crucial consideration when dealing with a substantial amount of missing data.

Assessing quality with distance metrics and predictive performances

In order to compare the methods, we have defined and computed several metrics for different settings:

Univariate analysis

We assess whether the distribution of each feature follows the same distribution in the original and synthetic datasets. To do so, we used a chi-squared test to compare categorical variables and a Wilcoxon test to compare continuous variables, with a significance level set to 0.05.

We use the chi-square test to determine if there is a significant difference between observed and expected frequencies across different categories. This test is commonly used to check for independence or association between categorical variables, assuming the variables are independent and the expected frequencies are not too small. In our case, we aim to have similar frequencies for each category in both the synthetic and original datasets.

The Wilcoxon test, a non-parametric test, is used to compare continuous distributions, particularly when the data does not follow a normal distribution. It does not assume normality and can handle skewed or heavy-tailed distributions. In our benchmark, we use the Wilcoxon test to verify that the distributions of the synthetic continuous variables are not statistically different from those of the original variables.

Correlations

We assess whether the bivariate distributions between each pair of features are preserved in the synthetic data. We compared the correlation matrices in the original and synthetic data by computing the mean absolute difference between the matrices. The analysis is performed on all variable pairs by calculating their correlation using two approaches. The lower triangular matrix was determined by computing Pearson’s correlation coefficient between continuous variables and Cramer’s V between categorical variables. The upper triangular matrix was dedicated to analyzing the relationship between continuous and discrete variables. To this end, we used the MIIC algorithm which has been shown to optimally discretize the continuous features by maximizing the mutual information for all potential cut-points on the continuous variables. If a discretization was found (there is a significant correlation between the features), Cramer’s V was then evaluated between the discrete and discretized variables. Also in this case the quality is directly associated with the difference between the correlation matrices. Small differences correspond to data that reliably capture the structure present in the original data. We define the correlation distance as the mean absolute difference between Correlation matrices ${C}^{S}$ (synthetic) and ${C}^{D}$ (original) as Eq. (1):

$${C}_{d}({C}^{S};{C}^{D})=\frac{1}{{p}^{2}}\mathop{\sum }\limits_{i=1}^{p}\mathop{\sum }\limits_{j=1}^{p}\left|{{C}_{{ij}}}^{S}-{{C}_{{ij}}}^{D}\right|$$

(1)

with p the total number of variables .

Mutual information (MI)

In order to compare bivariate associations we used mutual information²⁵, which is a measure of dependence between two variables. The concept of mutual information is linked to the entropy of random variables, rooted in information theory. MI has been shown to robustly capture the association between variables even when their relationship is nonlinear. Just like correlation matrices are obtained by computing the correlation between variables, MI matrices are obtained by computing the MI between all variables in the dataset. We estimated the MI for discrete-continuous or continuous-continuous variables through the optimum discretization algorithm implemented in the MIIC package. The quality of the generated data is directly derived by computing the mean absolute difference between the MI matrices of the original data and the one of the generated data. Small differences correspond to data that reliably capture the underlying structure present in the original data. As with correlation matrices, we define the mutual information distance as the mean absolute difference between Mutual information matrices $M{I}^{S}$ (synthetic) and $M{I}^{D}$ (original) as Eq. (2):

$${{MI}}_{d}(M{I}^{S};\,M{I}^{D})=\,\frac{1}{{p}^{2}}\,\mathop{\sum }\limits_{i=1}^{p}\,\mathop{\sum }\limits_{j=1}^{p}\,\left|M{{I}_{{ij}}}^{S}-\,M{{I}_{{ij}}}^{D}\right|$$

(2)

with p the total number of variables .

Multivariate distributions

To assess whether the joint multivariate distribution is preserved in the synthetic dataset we computed the Wasserstein distance (earth mover’s distance) between the original and the synthetic data, using the synthcity²¹ package. The main advantage of using Wasserstein compared to other metrics, such as the Kullback-Leibler divergence for instance, is that it is a proper distance with the associated properties such as symmetry and does not require both measures (original and synthetic) to be on the same probability space. A small Wasserstein distance corresponds to synthetic data that reliably represent the multivariate distribution.

Predictive performances

One way to evaluate the quality of a dataset is to assess if the generated data can be used to perform classical machine learning tasks such as supervised learning. We therefore chose to compare the algorithms based on their capability to build a relevant machine learning model to predict overall survival using a survival random forest model. We also evaluated whether each synthetic dataset retains robust relationships by comparing variable permutation importance ranking with the “true” ranking obtained on the original dataset. We made this comparison using survival Random Forest as the machine learning algorithm. To achieve this, a K-fold cross-validation approach (K = 5) was employed, where for each fold, the model was trained on 75% of the synthetic data and evaluated on a 25% hold-on test from the real data (the samples in the hold-out test set were selected to ensure that they were not used for training the generative model).

Assessing privacy metrics by identifiability score and membership inference

In this study we implemented different approaches to identify the level of privacy for each synthetic data generation method. In 2006 the paradigm of differential privacy was introduced and is still to date one of the most used techniques to try to preserve data privacy through mathematical constraints²⁶. However, differential privacy has been shown to not fully mitigate the risk of re-identification. Stadler and colleagues have shown that under certain circumstances, neither the original implementation of PrivBayes nor PATEGAN²⁷ (Private Aggregation of Teacher Ensembles Generative Adversarial Network) reliably prevents linkage attacks, leaving some samples vulnerable to membership inference attacks²⁸. Moreover, it has been reported in many scenarios that strong differential privacy constraints lead to the generation of synthetic data exhibiting a disrupted correlation structure between features, making the resulting data problematic²⁴ (Fig. 3).

Revisiting Identifiability score (IS)

To ensure data privacy, generated synthetic patient records should be “different enough” from the original patient records. Following this idea, we used a framework for the evaluation of privacy risks developed by Yoon and colleagues who proposed a new concept for identifiability²⁹. Yoon and colleagues define an identifiability property related to the minimum distance between real patients and the distance between real and synthetic samples. In order to weight each feature according to its probability of identifying patients having the same values, authors used a weighted Euclidean distance as metric, giving more weight to features having an unbalanced distribution of events. Authors define ε-identifiability as the property of having less than ε ratio observations from the original dataset in the generated synthetic dataset that are “not different enough” from the original observations. ε corresponds to the defined identifiability score. In this scenario, an identifiability of zero would represent a perfectly non-identifiable (private) dataset and an identifiability of one would represent a perfectly identifiable dataset. The proposed identifiability is defined for all the samples or variables. The described identifiability distance is implemented in the Synthcity package. The derived privacy score is then defined as 1 - identifiability score.

Adapting membership inference score (MIS)

Secondly, inspired by the work of El Emam K et al.³⁰ and J. Yoon et al.²⁹, we also proposed to compute a membership inference metric. We used the partitioning membership disclosure attack method proposed by El Emam K and colleagues where, instead of using the hamming distance between samples as a similarity measure, we used a weighted Euclidean distance where the weights are defined as the entropy of each feature, as proposed by J. Yoon et al.²⁹.

Moreover, to ensure a reliable distance metric with mixed variables (a combination of variables with either categorical or continuous domains), we have taken the following additional steps:

• Apply a Multiple Factor Analysis for Mixed Data (using the FactoMineR package³¹) to reduce the dimensionality of the data.

• Compute the Euclidean distance between samples in the space of the 10 first principal components as a similarity measure. It has the benefit of keeping the notion of Euclidean distance valid and meaningful.

This score evaluates whether we are able to identify which patients were used to create the synthetic dataset by subsampling the original dataset into a training and test set, for varying sample size. The derived privacy metric is then defined as 1 - membership inference score.

Trade off between Quality and Privacy: the Quality-Privacy Score (QPS)

Literature results³² and our findings manifestly suggest the necessity of a trade-off between data quality and data privacy. On the one hand, small modifications of the original data are directly associated to good quality scores but to poor privacy ratings, since almost all the information of the dataset is maintained. On the other hand, strong perturbations or noise addition lead to a net loss on quality of the synthetic data with a concomitant gain on privacy.

This problem is analogous to the classical machine learning dilemma of obtaining good precision and recall scores, simultaneously, which calls for defining a trade-off measure such as the F₁ score measure, defined as the harmonic mean between precision and recall scores as Eq. (3)

$${F}_{1}=2\times \frac{{Precision}\times {Recall}}{{Precision}+{Recall}}$$

(3)

Inspired by the F₁ score definition, we formulated a version of quality versus privacy trade-off by adapting the classical F₁ formula above. This requires defining data quality and privacy scores in the range [0,1], where best score values correspond to 1.

To this end, we normalized each quality and privacy metric by a reference value, namely those computed on the data generated by the Random method.

We define as normalized quality each of the previously described quality measures divided by the corresponding reference value as Eq. (4):

$$Q(M{I}^{S})=\,1\,-\frac{M{I}_{d}(M{I}^{S};\,M{I}^{D})}{{{MI}}_{d}(M{I}^{R}\,;\,M{I}^{D})}\,,$$

(4)

where $Q(M{I}^{S})$ is the normalized quality for mutual information of synthetic dataset, $M{I}^{S},{M}{I}^{D}$, and $M{I}^{R}$ are the mutual information matrices of, respectively, the synthetic data, the original data, and the random data, and $M{I}_{d}({X;Y})$ is the mutual information distance between mutual information matrices $X$ and $Y$, as defined in “Results”.

We define similarly the normalized quality for Wasserstein distance as Eq. (5):

$$Q({{W}_{p}}^{S})=\,1\,-\frac{{W}_{p}({\mathcal{X}}^{S};\,{\mathcal{X}}^{D})}{{W}_{p}({\mathcal{X}}^{R}\,;{\mathcal{X}}^{D})},$$

(5)

where $Q({{W}_{p}}^{S})$ is the normalized quality for Wasserstein distance of the synthetic dataset, ${{\mathcal{X}}}^{S}$, ${{\mathcal{X}}}^{D}$, ${{\mathcal{X}}}^{R}$ are the distributions of the synthetic, original and random datasets respectively and ${W}_{p}({\mathcal{X}};{\mathcal{Y}})$ is the Wasserstein p-distance between distributions ${\mathcal{X}}$ and ${\mathcal{Y}}$.

Finally we define the normalized quality for correlation distance as Eq. (6):

$$Q({{C}_{d}}^{S})=\,1\,-\frac{{C}_{d}({C}^{S}\,;\,{C}^{D})}{{C}_{d}({C}^{R}\,;\,{C}^{D})},$$

(6)

where $Q({{C}_{d}}^{S})$ is the normalized quality for correlation distance of the synthetic dataset, ${C}^{S}$, ${C}^{D}$, ${C}^{R}$ are the correlation matrices of the synthetic, original and random datasets and ${C}_{d}({X};Y)$ is the correlation distance between correlation matrices $X$ and $Y$, as defined in “Methods”.

In the same way, normalized privacy is defined as Eq. (7):

$$N{P}_{{IS}}=\,1\,-\frac{I{S}_{S}}{I{S}_{R}},$$

(7)

with $I{S}_{S}\in \,[\mathrm{0,1}]$ and $I{S}_{R}\in [\mathrm{0,1}]$ the identifiability scores of the synthetic and random datasets respectively.

Similarly we define the normalized membership inference score, as Eq. (8):

$$N{P}_{{MIS}}=\,1\,-\frac{{MI}{S}_{S}}{{MI}{S}_{R}},$$

(8)

with ${MI}{S}_{S}\in \,[\mathrm{0,1}]$ and ${MI}{S}_{R}\in [\mathrm{0,1}]$ the membership inference scores of the synthetic and random datasets respectively.

In this setting, we define our Quality-Privacy scores as the harmonic mean of the normalized quality and privacy scores, as Eq. (9):

$${QPS}=\,2\,\times \frac{{NQ}* {NP}}{{NQ}+{NP}},$$

(9)

with ${NQ}\in \{\,{Q}_{M{I}_{D}},\,{Q}_{W},\,{Q}_{{C}_{d}}\}$ and ${NP}\in \,\{N{P}_{{MIS}},\,N{P}_{{IS}}\}.$

In addition, to facilitate benchmark comparison between different synthetic data generation methods, we have also designed two global scores to highlight the performance across the 3 quality metrics (Wasserstein, Mutual Information, correlation) and the 2 privacy metrics (Membership inference and identifiability) used in this study. We will refer to these global scores as ${MetaQP}{S}_{{am}}$ and ${MetaQP}{S}_{{hm}}$ in the rest of the paper.

${MetaQP}{S}_{{am}}$ corresponds to the F1-score between the arithmetic mean of the quality scores and the arithmetic mean of the privacy scores, defined as:

$${metaQP}{S}_{{am}}=\,2\,{[3/({Q}_{M{I}_{D}}+{Q}_{W}+{Q}_{{C}_{d}})+2/(N{P}_{{MIS}}+N{P}_{{IS}})]}^{-1}$$

(10)

${MetaQP}{S}_{{hm}}$ corresponds to the F1-score between the harmonic mean of the quality scores and the harmonic mean of the privacy scores, defined as:

$$\begin{array}{l}{metaQP}{S}_{{hm}}=\,2\,\left(\left[{{Q}^{-1}}_{M{I}_{D}}+{{Q}^{-1}}_{W}+{{Q}^{-1}}_{{C}_{d}}\right)/3 \right. \\ \qquad\qquad\qquad\;\;\; \left. +\,(N{{P}^{-1}}_{{MIS}}+N{{P}^{-1}}_{{IS}})/2\right]^{-1}\end{array}$$

(11)

${MetaQP}{S}_{{am}}$ and ${MetaQP}{S}_{{hm}}$ could be readily adapted to include other quality and privacy scores, if needed. Hence, the rationale of the ${MetaQPS}$ metrics is to first take the arithmetic or harmonic means over all quality and privacy scores, separately, before quantifying the global quality versus privacy trade-off using an F1-score measure. While the ${MetaQP}{S}_{{am}}$ metric, based on arithmetic means tends to equally weigh the contributions of each quality and privacy scores, the ${MetaQP}{S}_{{hm}}$ metric, based on harmonic means, gives more weights to lower individual quality and privacy scores and is therefore expected to be more sensitive to the most discriminative quality and privacy scores.

Benchmark datasets

This paper aims to provide a comprehensive benchmark specifically focused on the anonymization of small, complex datasets with high privacy risks. To ensure the relevance and robustness of the comparison, we intentionally included a diverse range of methods including Bayesian and constraint-based approaches as well as Deep learning methods. However, it is important to note that Deep Learning methods like CTGAN, medWGAN, and TVAE require larger sample sizes for effective convergence. To address this specificity, we chose to incorporate three datasets of various sizes to assess the performance of each method on a wide range of sample sizes (from 100 to 20,000 patients).

Breast cancer (METABRIC)

The METABRIC (Molecular Taxonomy of Breast Cancer International Consortium) dataset is a collection of over 2,000 clinically annotated primary breast cancer specimens obtained from tumor banks in the UK and Canada³³. The cohort encompasses clinical variables and genetic information including copy number alterations, copy number variations, and single nucleotide polymorphisms. The METABRIC dataset was selected for this study due to its widespread usage and validation in the literature, as well as its suitable sample size for the application of machine learning algorithms and coexistence of numerical and categorical features. The original dataset, consisting of 2491 patients and 36 variables, was pre-processed by removing patients with >20% missing values and variables with unique values. The resulting filtered dataset comprised 1977 patients and 29 clinical variables, with 19 of them being discrete and 10 continuous. Figure 2 reports the DAG obtained by using the MIIC-to-DAG algorithm (step 2B in Fig. 1), which was applied on the network reconstructed by the MIIC algorithm, shown in Supplementary Fig. 2. The graph contains 63 edges reporting direct association between the 29 variables. Unconnected nodes represent features that are not associated with any other variable in the data (following MIIC residual mutual information evaluation). It is important to remember that the MIIC algorithm does not have hyperparameters, does not need any tuning, can deal with missing data and is not sensible to the order of features in the data. The used data comes from public data available in the cBioPortal repository: https://www.cbioportal.org/study/summary?id=brca_metabric.

Fig. 2: Network reconstructed by MIIC-to-DAG starting from the network obtained by MIIC from the full METABRIC dataset.

The network is learned with the MIIC-to-DAG algorithm (step B of MIIC-SDG) starting from the network obtained by MIIC, Supplementary Fig. 1, with the parameters defined in Supplementary Table 1. This network corresponds to the directed acyclic graph used to generate the synthetic data for the step C of MIIC-SDG. This network is visible at the following address: https://miic.curie.fr/job_results_NL.php?id=METABRIC_DAG.

Details about the METABRIC patient population, consents, approvals, tissue collection and sample processing are provided in the publication by Curtis et al.³³ All patient specimens were obtained with appropriate consent from the relevant institutional review board. The data are available at the European Genome-phenome Archive (http://ebi.ac.uk/ega/), which is hosted by the European Bioinformatics Institute, under accession numbers EGAS00000000083.

Bladder cancer

To extend our assessment of synthetic data generation approaches, we integrated a second dataset derived from a Roche clinical trial on bladder cancer (Phase II single-arm study IMvigor210³⁴). The study investigated metastatic urothelial cancer treatment with the anti PD-L1 agent atezolizumab and highlighted key factors influencing outcomes, such as the presence of a CD8 + T-effector cell phenotype and the burden of neoantigens and tumor mutations. These known key outcomes were then also used as a quality metric in our assessment.

IMvigor210 was a multicentre, single-arm, phase 2 trial that investigated efficacy and safety of atezolizumab in metastatic urothelial cancer. This trial was done in 47 academic medical centers and community oncology practices across seven countries in North America and Europe. All patients provided written informed consent before study entry. The study was done in accordance with the Declaration of Helsinki and International Conference of Harmonization Good Clinical Practice guidelines. The trial is registered with ClinicalTrials.gov under the following number: NCT02951767 for cohort n°1 and NCT02108652 for cohort n°2. The protocol was approved by institutional review boards or independent ethics committees at participating study sites. The data has been made available through an R package on the following website: http://research-pub.gene.com/IMvigor210CoreBiologies/.

This addition enriches our benchmark with a second real and practical use case coming from our organization. It also helps validate the overall applicability of our approach to different sets of data, varying both in dimensionality and in the types of variables analyzed. Specifically, IMvigor210 included 310 participants with 297 known outcomes. We further restricted the benchmark to 24 features keeping a balanced mix of continuous and discrete variables.

Diabetes

Diabetes is among the most prevalent chronic diseases, impacting around 500 million people worldwide. Diabetes is a serious chronic disease in which individuals lose the ability to effectively regulate levels of glucose in the blood, and can lead to reduced quality of life and life expectancy.

To test our algorithm on larger sample sizes, we added a third dataset related to Diabetes. This dataset originates from the 2015 Behavioral Risk Factor Surveillance System (BRFSS) dataset, sourced from telephone surveys, encompassing USA residents’ health behaviors, conditions, and socio economic aspects³⁵. As stated by the Behavioral Risk Factor Surveillance System, data and materials produced by federal agencies are in the public domain and may be reproduced without permission.

It is often used for machine learning purposes and is also publicly available on Kaggle, the version we used is available at this address: https://www.kaggle.com/datasets/alexteboul/diabetes-health-indicators-dataset.

It contains factors influencing diabetes disease and other chronic health conditions related to diabetes. The full dataset contains 253680 samples and 22 features.

Benchmark setting

We evaluated the different algorithms by subsampling the whole 1977 sample METABRIC dataset in different subsample sizes: 50, 100, 200, 500, 1000, 1500 and 1977. This allows one to assess the performance of each method in multiple subsets along with their stability. We created 10 datasets for each sample size and each one of them was used to generate 10 synthetic datasets with a different seed (100 datasets for each sample size). It is important to note that seed effects are different in each algorithm. For the IMvigor210 study we chose to analyze the dataset in subsets of 100, 200 and 297 samples. For Diabetes, we analyzed the algorithm performances on larger sample sizes: 500, 1000, 5000, 10000 and 20000.

Results

Univariate distribution comparison as a per variable analysis

When comparing two datasets that share the same set of features, the simplest analysis we can conduct involves assessing the distribution of each variable within both the original and synthetic datasets. Table 1 presents the average count of features that exhibited statistically significant differences based on these two tests across various sample sizes (columns) and algorithms (rows). The standard deviation is provided in parentheses. The results indicate that Synthpop is the most effective method for replicating univariate distributions, followed closely by Bayesian algorithms and MIIC-SDG, which demonstrated similar performance. Conversely, the other algorithms fell short in reproducing the univariate distribution, with between 16 (CTGAN and TVAE) and 21 features exhibiting differences in the largest sample size. As expected, the random method flagged nearly all variables as different, owing to its random sampling approach within the original feature range.

Table 1 Average number of significantly different features between real and synthetic distribution on METABRIC dataset

Bivariate analysis to assess associations between variables

Mutual Information (MI) distance

Mutual information distances are evaluated by calculating the mutual information difference between real and synthetic data, evaluating it for all pairs of variables. The results are presented in Supplementary Fig. 2. The data generated by the MIIC-SDG algorithm reproduces well the mutual information between variables present in the original data, obtaining better scores than other methods for small sample sizes (50 and 100 samples). With an increasing number of samples the mutual information is best reproduced by Synthpop, with MIIC-SDG positioning at second or third place (close to bayesian tree search). MedWGAN scores at the fourth place. CTGAN obtained the lowest score on the smallest sample size, and eventually improved its performance with larger sample sizes. TVAE and the Bayesian hill climbing technique scored closely on the largest datasets, with Bayesian hill climbing reaching the fourth or fifth position in smaller samples (<500 samples).

Correlations (Corr) distance

Supplementary Figure 3 reports the correlation distances, defined in “Methods”, between synthetic data and the corresponding original data. It can be observed that the Bayesian tree search and Synthpop algorithms have comparable performances, both for low and high sample sizes. MIIC-SDG has better results than competitors on small sample sizes (<200 samples) but the gain in performance obtained by increasing sample sizes stabilizes at higher values compared to the first two competitors. CTGAN obtained low scores for smaller sample sizes (<500 samples), but the performance increases fast with increasing the number of samples, obtaining similar scores to MedWGAN. TVAE fails to capture the correlation structure, even if it is improved with 1500 samples. Bayesian hill climbing with BIC criterion does not obtain competitive scores, even with large sample sizes. PrivBayes exhibit similar results to the random data method, showing a complete loss of correlation patterns. Globally, MIIC-SDG, CTGAN and MedWGAN obtained similar scores at large sample sizes.

The correlation matrices for the METABRIC datasets (using 1000 samples) are shown in Fig. 3. Values are obtained as a mean correlation over all executions from running the algorithms on the 1000 sample datasets (using bootstrap) and using multiple seeds.

Fig. 3: Correlation matrices evaluated on 1000 samples for METABRIC dataset.

Correlation for each x, y combination is evaluated as the mean value over all executions with the same sample size.

The performance of the different methods are, in order: Bayesian with tree search algorithm, Synthpop, CTGAN, MIIC-SDG and medWGAN with the same score, TVAE and PrivBayes. As expected, the score of the random method is by far the lowest one and it is strongly dependent on the type of associations between variables that exist in the original data (correlation structure and strength). As shown in Supplementary Fig. 12, we compare the correlation matrices for the Diabetes dataset in a scenario where the correlation structure is much sparser, with only a few features being correlated. In this context, using the mean correlation distance to differentiate between algorithms is less meaningful. Random values can exhibit a low mean correlation distance because most features are uncorrelated, and introducing random values does not significantly impact the overall correlation. Therefore, in such cases, distinguishing between algorithms in terms of correlation distances becomes more challenging.

Multivariate distribution comparisons as a global metric to evaluate quality

Wasserstein distance

The results of the multivariate Wasserstein distance assessments are presented in Supplementary Fig. 4. In this multivariate setting the Bayesian network approach with tree search estimation reached the best scores with very small distances, followed by Synthpop and medWGAN at similar scores, MIIC-SDG at the fourth place, and Bayesian hill climbing (using BIC criterion), with CTGAN and TVAE in similar ranges. The differential privacy bayesian approach with epsilon set to 1 generates datasets with much higher distances compared to the other benchmarked methods.

From these results, we can notice that there are large gaps between the different methods, with the Bayesian (tree search estimation) approach giving much better results than competitors. In Supplementary Fig. 4, we can observe that the Bayesian tree search approach generates synthetic categorical variables on the METABRIC dataset that closely resemble the original distribution. However, the performance difference is less pronounced for continuous variables. The Bayesian approach demonstrates overall good performance, which can be attributed to the METABRIC dataset being predominantly composed of categorical variables. This gives an advantage to methods that excel in handling such variable types.

When computing the Wasserstein distance using only continuous features, we observe that Bayesian tree search obtains indeed similar scores with respect to Synthpop and MIIC-SDG. Similarly, MedWGAN obtains good scores mostly on categorical variables, but performs slightly less well on continuous variables, which might be due to the low sample size used to train the model.

Machine learning performance: Predicting Overall Survival (OS) response

The aim of this part is to evaluate the ability of synthetic data generation algorithms to preserve multivariate information for the purpose of predicting survival features. Figure 4 represents the feature importance for the prediction of Overall Survival (SO) in the original data and in all benchmark algorithms. We note that MIIC-SDG, Synthpop, CTGAN and medWGAN all predict the same three main features (Nottingham Prognostic Index, Number of positive lymphatic nodes and Tumor size) as the most important features for OS prediction. Figure 5 shows the concordance index estimates from Survival Random Forest model to predict Overall Survival. While MIIC-SDG does not outperform a number of benchmark methods in terms of OS prediction, it is important to keep in mind that the ability to predict a target variable (OS in this case) from other features can also be used as a metric for privacy risk, as it can be seen as an inference attack on sensitive attributes. Having a high concordance with the true data also correlates to a high risk in the case of inference attacks.

Fig. 4: Features permutation importance to predict overall survival.

We used a Survival Random Forest model fitted on a set of 1977 patients from the METABRIC dataset.

Fig. 5: K-Fold Cross-validated c-index estimates.

This analysis was made using a Survival Random Forest model to predict Overall Survival in the METABRIC dataset in function of sample size (K = 5).

Re-identification as a metric to evaluate privacy level

Identifiability score

The identifiability score corresponds to the probability of re-identification given the combination of all data on any individual patient. It is evaluated by measuring the identifiability of the finite original patient data using the finite generated synthetic data. Supplementary Figure 5 shows the privacy score of the synthetic data generation algorithms evaluated as (1 - Identifiability), as a high identifiability score indicates low privacy. The Bayesian algorithm with tree search has the lowest privacy scores (0.23–0.44), followed by the Synthpop algorithm (0.44–0.49), MIIC-SDG (0.45–0.6), TVAE (0.47–0.76), CTGAN (0.59–0.81), Bayesian with hill climbing (0.71–0.87), PrivBayes (0.94–0.99) and Random (0.97–1), with numbers between parenthesis corresponding to the smallest and biggest sample sizes. Interestingly, the random algorithm did not reach 1 for the smallest sample sizes.

Membership inference score

The membership inference score corresponds to the probability of identifying which patients have been used to generate the synthetic dataset. Supplementary Figure 6 shows the privacy score of the synthetic data generation algorithms evaluated as (1 - membership score), as a high membership score indicates low privacy. Bayesian tree search algorithm is the method with lowest privacy as it is easy to guess if a sample has been used or not to generate the synthetic data, followed by the Synthpop method, where privacy scores never increase above 0.5. MIIC-SDG remains at the third position, with privacy scores increasing well with larger sample sizes. CTGAN obtains slightly better results in the membership inference attack, together with TVAE. Bayesian hill climbing generates datasets where it is hard to guess the membership of samples in the original data, while PrivBayes and the random algorithm obtain best privacy scores, with values close to 1.

Quality-Privacy Scores (QPS) as a trade-off between quality and privacy

Quality-Privacy scores can be evaluated by using different metrics for both quality and privacy. Both dimensions have been evaluated by calculating the ratio between the value obtained using the data of each algorithm and the value obtained using the corresponding random data, so that both quality and privacy range in [0,1] (normalized formula). For quality measures we focused on the normalized Mutual Information distance that reliably captures bivariate associations and clearly discriminates the different approaches. As privacy metrics we considered the results obtained with the identifiability and the membership inference scores, in their normalized version. QPS are then obtained by taking the harmonic mean of the normalized quality and privacy scores, for each combination of quality-privacy measures, as introduced in the Method section. In addition, in order to facilitate the comparison of synthetic data generation methods across multiple quality and privacy scores, we also introduced two global QPS metrics, metaQPS_am and metaQPS_hm, based, respectively, on the arithmetic means and harmonic means of several quality scores and privacy scores, as detailed in Methods.

In Fig. 6 we show the mutual information quality metric and the two privacy scores as well as the two derived QPS (one for each privacy metric). Based on the QPS derived from mutual information distance, the MIIC-SDG method is ranked as the best algorithm in terms of the quality-privacy trade-off for both QPS metrics. It is only outperformed by Synthpop for large sample sizes when considering the Membership inference as the privacy score. However, it is important to notice that the privacy evaluated from the identifiability score is always smaller than 0.5 for Synthpop, a value much lower to the one obtained through MIIC-SDG, ranging in 0.6–0.7 for higher sample sizes (>200 samples). This makes synthetic data generated with Synthpop significantly less private than synthetic data generated with MIIC-SDG. The QPS obtained using MI distances thus highlights MIIC-SDG ability to reliably generate quality synthetic data while best preserving the privacy of the original sensitive data.

Fig. 6: Quality, privacy and quality-privacy scores (QPS).

This comparison is made using Mutual Information distance as quality measure and privacy evaluated using identifiability and membership inference scores.

We also analyzed the results obtained with the other quality distances, the two privacy measures and the corresponding QPS (4 supplementary metrics). These complete results are shown in Supplementary Fig. 7. MIIC-SDG algorithm obtained the best QPS results for correlation distance for small sample sizes (<500 samples) and obtained the second or third best scores after the CTGAN and medWGAN for the largest sample sizes. Based on the QPS obtained using the Wasserstein distance and Identifiability scores, the Bayesian hill climbing algorithm emerges as the top-performing method, followed closely by CTGAN, MIIC-SDG, and TVAE, all exhibiting similar scores. In this scenario Synthpop does not show competitive results due to a poor privacy score. Bayesian tree search and PrivBayes score poorly as well, the first due to a low privacy score and the second due to a low quality of the generated data.

We then run the same pipeline on the second dataset (IMvigor210), presented in Fig. 7, obtaining comparable results to the ones on the METABRIC data. Also in this case MIIC-SDG shows better results than competitors based on the mutual information QPS, reporting a good trade-off between quality and privacy scores. Supplementary Figure 10 provides detailed information on the QPS, quality, and privacy scores for the IMvigor210 dataset. In this scenario, MIIC-SDG scores rank either first or second in terms of QPS (and third when tied with Synthpop), using correlation as the distance metric. However, QPS ranks using Wasserstein distance do not effectively differentiate between the best methods, which all perform essentially the same, as observed on the METABRIC dataset.

Fig. 7: Quality, privacy and quality-privacy scores (QPS) on IMvigor210.

This comparison is made using Mutual Information distance as quality measure and privacy evaluated using identifiability and membership inference scores. Data from the IMvigor210 trial (Bladder cancer).

Finally, we benchmarked the different synthetic data generation methods on a larger dataset, Diabetes (500 to 20,000 samples). The results reported in Supplementary Fig. 11 show that MIIC-SDG shares, together with Synthpop, the top-ranking QPS score based on mutual information, with MedWGAN also reaching similar high scores at large sample sizes (>1000 samples). However, the three methods cannot be seen as equivalent in all contexts, as Synthpop exhibits a significantly higher quality with concomitant lower privacy, whereas medWGAN exhibits a higher privacy but lower quality overall. By contrast, MIIC-SDG appears to achieve a better balance between privacy and quality defined in terms of MI distances. Using other quality metrics, MedWGAN is shown to achieve the best QPS tradeoff based on correlation distance but the worst Wasserstein distance overall. Yet, as with the first two datasets, the Wasserstein distance did not provide a discriminative ranking of the best performing methods.

Figure 8 summarizes these results by integrating all quality and privacy scores into single metaQPS metrics for each dataset and all sample sizes analyzed in this study. This figure demonstrates the good overall performance of MIIC-SDG algorithm, particularly at small sample sizes, while other state-of-the-art methods, such as Synthrop, CTGAN and medWGAN, achieve better or similar performance at large sample sizes. Among the Bayesian methods included in this study, Bayesian hill climbing and Bayesian tree search exhibit somewhat lower performance, but significantly outperform privBayes. This suggests that the incorporation of differential privacy into privBayes adversely impacts the overall quality of the generated synthetic data. All in all, we note that the metaQPS_hm metric, based on the harmonic means of the quality and privacy scores, provides a more stringent evaluation of synthetic data generation methods by highlighting the most discriminative quality and privacy scores integrated in the global metaQPS_hm metric. By contrast, the arithmetic means of individual quality and privacy scores integrated in the metaQPS_am metric tend to be less discriminative. We would therefore recommend using the metaQPS_hm metric to integrate several quality and / or privacy scores in future comparative studies of synthetic data generation methods.

Fig. 8: Meta-QPS scores of each dataset (IMvigor210, Metabric and Diabetes).

These plots summarize the benchmark results by integrating all quality and privacy scores into single metaQPS metrics for each dataset and all sample sizes analyzed in this study. MetaQPS.am corresponds to the F1-score between the arithmetic mean of quality scores and the arithmetic mean of the privacy scores. MetaQPS.hm corresponds to the F1-score between the harmonic mean of quality scores and the harmonic mean of the privacy scores (see details in Methods).

Discussion

Over the past few decades, there has been a significant increase in the recruitment of patients for clinical trials and the collection of real-life health-related datasets. This surge has been witnessed in both public institutions and private companies, resulting in the accumulation of vast amounts of patient information. As the number of collected studies continues to grow, it becomes increasingly urgent to explore effective solutions for harnessing this wealth of data. This entails facilitating new research initiatives and promoting data sharing, all with the ultimate goal of pushing the boundaries of medical research. In recent years, various machine learning and deep learning approaches have been employed to synthesize health data. These approaches hold the promise of enabling data sharing while safeguarding patient privacy. Regulatory standards such as the European General Directive on Data Protection (GDPR) mandate that data holders implement robust measures to ensure data security and prevent potential data breaches, often leading to restrictions on data sharing and secondary data usage. However, few established standards exist to guarantee adequate data anonymization and data security. Previously proposed methods like k-anonymity, l-diversity, and t-closeness have limitations when it comes to preserving privacy while maintaining sufficient data quality for research purposes. Therefore, the development of new quantitative standards is imperative to facilitate data anonymization through the generation of synthetic data and assess the level of risk associated with data publication. Synthetic data generation offers several opportunities that can be categorized as follows: firstly, as a tool for collaborative projects thanks to the straightforward and time-efficient sharing of data; secondly, as a pre-production platform for development; and finally, for deriving insights from data. The first two application types typically do not necessitate the faithful reproduction of complex statistical features found in the original datasets. However, the generation of insights relies on the synthetic data generator’s ability to preserve intricate data patterns, including those not yet identified in the original dataset. Indeed, the estimation of the joint multivariate distribution of clinical trials is a hard task due to the limited sample size of such datasets. It is therefore crucial to identify synthetic data algorithms that are able to operate on such a scale and provide meaningful results.

In order to identify a suitable algorithm for synthetic data generation applicable to biomedical/clinical data, it is essential to consider the preservation of data quality and the protection of privacy simultaneously. To address this challenge, we conducted a comprehensive evaluation of the various state-of-the-art algorithms across multiple scenarios, examining data quality and privacy both separately and more importantly in combination. To evaluate the impact of sample size on each algorithm’s performance, we used datasets of varying sizes: small (ranging from 50 to 200 samples), medium (500–2000 samples), and large (5000–20000 samples).

Our approach involved the following steps:

• 1. Defining Quality Metrics: we first established various metrics for assessing the preservation of data quality. These metrics were designed to gauge the ability of the methods to generate data that closely resembles the original dataset. One of the most used methods to compare data have been performed through the Pearson correlation coefficients. However, Pearson correlation is also known to be very sensitive to outliers, which may explain some of the apparent good relative rankings of certain methods under correlation scores, while they exhibit poorer performance under more robust statistical criteria such as MI, which only depends on the ranks (not the specific values) of the variables of interest. We hence focused our analysis on MI, but we also presented results using the more classical correlation concept.

• 2. Privacy Considerations: we then focused on the privacy of the original sensitive data. Our aim was to prevent the re-identification of patients and safeguard against the disclosure of sensitive patient information.

• 3. Defining trade-off metrics: To provide a comprehensive assessment of the sensitive synthetic data generated, we proposed to combine the quality and privacy metrics. The resulting combination of metrics introduced in the paper defines novel pairwise and global quality-privacy scores, the QPS and metaQPS metrics, which we used to rank all the algorithms included in our benchmark.

Our novel SDG method (MIIC-SDG) provides good overall performance in terms of quality-privacy tradeoff, especially at small sample size, while other state-of-the-art methods, such as Synthrop, CTGAN, and medWGAN, achieve better or similar performance at large sample sizes, Fig. 8. MIIC-SDG, which integrates graph learning and information theoretic approaches, retains complex association patterns, including those that remain undiscovered in the original dataset, making it suitable for extracting novel insights from sensitive biomedical data. Other methods approximating the full joint distribution, such as Synthpop, are also capable of preserving these complex association patterns, although they typically present a higher risk of patient re-identification. By contrast, methods that focus on preserving more limited aspects of the data, like first-order correlations, are not well-suited for novel insight generation, although they may suffice for pre-production algorithmic development purposes. Furthermore, it is important to keep in mind that SDG methods utilizing GAN or VAE approaches, such as CTGAN, medWGAN and TVAE, require large sample sizes to achieve stable results. This characteristic explains why they tend to achieve lower performance on small datasets, such as Metabric and IMvigor210. On the other hand, on larger datasets, such as Diabetes, GAN approaches achieve performance at par with the best SDG methods in terms of QPS ranking.

These results confirm that Deep Learning approaches are definitely relevant when the sample size is large enough to properly train them, as already evidenced by their success in generating synthetic Electronic Health Records (EHR) from datasets with tens of thousands of records^6,7,12. However, in the specific context of small and complex biomedical datasets, typically found in clinical studies, the relevance and benefits of Deep Learning approaches is not as apparent, especially in terms of information preservation.

MIIC-SDG stands out particularly well for generating synthetic datasets that contain mixed data types and a low number of samples (<1000), a characteristic typically observed in actual clinical datasets. The method is also well-suited for handling longitudinal data, where measurements are taken at various time points.

This paper also introduces novel pairwise and global quality-privacy scores (QPS and metaQPS), which aim to quantify the tradeoff between quality and privacy measures in the evaluation of synthetic health data generation methods. These scores are designed to be bounded between 0 and 1 such that a QPS = 0 represents a randomized dataset. However, while reaching the theoretical maximum value of 1 may be difficult or impossible in practice, these scores can still be used to compare and rank different SDG methods, similar to how relative F1-scores are used to compare and rank ML methods.

An important feature of pairwise QPS metrics is their focus on a specific pair of quality and privacy scores. Indeed, SDG methods need to be assessed in context and certain quality or privacy criteria might be preferable to others in different contexts. For instance, while Synthpop, MIIC-SDG and medWGAN shared top-ranking QPS scores based on mutual information on the Diabetes dataset (Supplementary Fig. 11), the three methods cannot be seen as equivalent in all contexts. Indeed, Synthpop exhibits a significantly higher quality with concomitant lower privacy, whereas medWGAN exhibits a higher privacy but lower quality overall (Supplementary Fig. 11). Hence, MIIC-SDG appears to achieve a better balance between privacy and quality defined in terms of MI distances, which likely stems from the information-based approach employed by MIIC.

By contrast, MedWGAN was found to achieve the best QPS tradeoff based on correlation distance but the worst Wasserstein distance overall (Supplementary Fig. 11). As correlation measures are well known to be highly sensitive to outliers, this may explain the favorable results of GAN methods with correlation quality metrics in general. Instead, MI is only sensitive to the rank (not the specific values) of variables, making it a much more robust quality score to outliers in the data. Finally, quality metrics derived from Wasserstein distances were found to be less discriminative than MI distances for ranking the best performing methods, which all reach similar Wasserstein scores in general.

To facilitate the overall comparison of SDG methods, we also introduced global performance scores integrating multiple quality and privacy scores. These metaQPS metrics provide a global indicator of each algorithm’s performance across all relevant quality and privacy scores and health datasets included in this study, Fig. 8. The two metaQPS metrics come with advantages and disadvantages. The metaQPSam metric, based on the arithmetic means of individual quality and privacy scores, equally weighs the contributions of each quality and privacy metrics. This tends to overlook the differences between SDG methods by masking their limitations on the most stringent quality or privacy measures. By contrast, the metaQPShm metric, based on the harmonic means of the quality and privacy scores, gives more weight to the most stringent quality and privacy scores. Hence, the metaQPShm metric is more conservative and better suited to highlight the differences between alternative SDG methods, due to its sensitivity to the most discriminative quality and privacy scores. MetaQPShm should therefore be favored in future comparative studies of SDG methods integrating several quality and / or privacy scores.

This study comes with limitations. First, we performed benchmark comparisons across a wide range of SDG methods and could not therefore include all available approaches beyond a few representatives of each class of SDG methods with open access and readily usable codes. Second, these benchmark comparisons are limited to three datasets and might not generalize to all possible health data, although we have tried to cover a wide variety of health datasets, including a broad range of sample sizes and mixed-type (continuous and categorical) variables. Third, this study primarily focused on a quantitative evaluation of the quality versus privacy tradeoff of SDG methods, with the introduction of novel pairwise and global QPS metrics. Yet, we recognized that other indicators, such as the overall survival prediction, are also important to assess the relevance of synthetic health data generation methods. Finally, the membership inference score, which requires a hold-out set for computation, could not be estimated for the entire datasets. This limitation could be overcome by employing a k-fold cross-validation procedure, as implemented in the TensorFlow Privacy Membership Inference Attack (MIA) Python library³⁶.

Likewise, the novel MIIC-SDG method reported in this paper has notable limitations, despites its good performance in terms of global quality-privacy scores, Fig. 8, especially at small sample sizes. First, MIIC-SDG does not rank among the best methods in predicting overall survival (OS) from a Survival Random Forest model, which suggests potential limitations in predicting specific tasks. Second, while MIIC-SDG achieves very good performance in terms of quality-privacy tradeoff based on mutual information (MI) distances, it does not display the best performance across all quality metrics. For instance, other methods such as medWGAN excel when correlation scores are used. Similarly, MIIC-SDG’s well-balanced performance in terms of quality-privacy trade-off implies that MIIC-SDG offers mid-range privacy scores and might not be the method of choice for applications requiring the highest level of data protection.

Considering these limitations and to better reflect the importance of quality versus privacy criteria in different contexts, a possible extension of the F1-based QPS scores, introduced here, would be to define Fα-based QPS scores. This extension would give different relative weights between quality and privacy criteria, enabling a stronger emphasis on either quality (α < 1) or privacy (α > 1) of synthetic data. Another possible modification to enhance the importance of privacy considerations would be to include other privacy scores, such as the nearest neighbor adversarial accuracy risk developed by Yale A et al.³⁷, in the global metaQPS metrics.

All in all, MIIC-SDG is particularly effective in generating synthetic data from biomedical datasets, which typically include a limited number of patients (<1000) and a complex multivariate joint distribution. In this context, MIIC-SDG tends to outperform or be comparable to other state-of-the-art methods (Fig. 8) with similar execution times (Supplementary Fig. 8). However, to generate synthetic health data from very large datasets, such as electronic health records, deep learning approaches may be more suitable.