Introduction

The crucial role of enzyme function annotation in our understanding of the intricate mechanisms driving biological processes governed by enzymes is widely recognized. The Enzyme Commission (EC) number, a numerical classification system commonly used for enzyme function, is a widely recognized standard in these efforts. The depth of insights provided by the EC number ranges from broad categories of enzyme mechanisms to detailed biochemical reactions through its four hierarchical layers of digits. Traditionally, sequence similarity-based methods, such as the basic local alignment search tool for protein (BLASTp)1 and HH-suite2, were largely relied upon for annotating EC numbers. However, in recent times, the deep learning revolution has largely solved the protein structure prediction problem, and it is natural to ask how these twin scientific advances can aid in enzyme function prediction3.

Predicting enzyme function is not merely an academic classification exercise; it holds immense practical value in systems biology and metabolic engineering, particularly in the construction of genome-scale metabolic models. Such predictive capabilities streamline the process of automating the curation of these models by improving the ability to predict which proteins are responsible for observed growth phenotypes under diverse nutrient conditions and distinct genetic backgrounds. Furthermore, precise knowledge of a genome’s metabolic capabilities enables the design of microbial cell factories to fit for purpose to the metabolic engineering goal, be it medicine, biomanufacturing, or bioremediation.

Currently, the majority of deep learning-based models developed for predicting EC numbers focus on either amino acid sequence or structural data of the enzyme. Studies such as that of DeepEC4, for example, rely solely on amino acid sequence data for EC number prediction. Conversely, the work in ProteInfer5 employs a single convolutional neural network to predict EC numbers, focusing more on the structural data. Additionally, a different approach integrating enzyme structure data into the training process is seen in DeepFRI6, which provides a more comprehensive view of the enzyme’s functionality. The recent addition of a contrastive learning method has also elevated the performance of EC number prediction7.

Building upon this groundwork, we propose CLEAN-Contact, a contrastive learning framework that amalgamates both amino acid sequence data and protein structure data for superior enzyme function prediction. Our CLEAN-Contact framework has shown a notable improvement over the current state-of-the-art, CLEAN7, under a variety of test conditions, further emphasizing the potential for combining protein sequence and structure-based deep learning in enzyme function predictive practices.

Results

Contrastive learning framework for enzyme functional annotation prediction combined with protein contact maps

We develop a deep contrastive learning framework aimed at predicting EC numbers. This framework integrates a protein language model (ESM-2)8 and a computer vision model (ResNet50)9 (See Methods). Protein language models excel at processing and extracting pertinent information from protein amino acid sequences, while computer vision models, especially convolutional neural networks (CNNs), demonstrate superior efficacy in handling image-like data, making CNNs well-suited for extracting relevant information from the square matrix structure of protein contact maps. Among protein language models, ESM-2 stands out with several advantages over its peers like ProtBert10 and ESM-1b11. These include more advanced model architectures, larger training dataset, and superior benchmark performance on the 14th Critical Assessment of protein Structure Prediction (CASP14)12 and Continuous Automated Model Evaluation (CAMEO)13. For the computer vision component, ResNet-50 offers an optimal balance between computational efficiency and performance in relevant tasks.

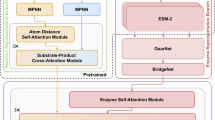
ESM-2 operates as a feedforward neural network, extracting function-aware sequence representations from input protein amino acid sequences. Meanwhile, ResNet50 functions as a feedforward neural network, extracting structure representations from input 2D contact maps derived from protein structures. The CLEAN-Contact framework plays a key role by combining these sequence and structure representations and employing contrastive learning to learn the prediction of EC numbers. The CLEAN-Contact framework consists of three key components: (1) The representations extraction segment (Fig. 1a), which is designed to extract structure representations from contact maps using ResNet509 and sequence representations from amino acid sequences using ESM-28. (2) The contrastive learning segment (Fig. 1b), where contrastive learning is performed to minimize the embedding distances between enzymes sharing the same EC number while maximizing the embedding distances between enzymes with different EC numbers. Specifically, structure and sequence representations are transformed to the same embedding space, leading to the same dimension for both structure and sequence representations. Subsequently, the combined representations are produced by adding the structure and sequence representations in the same embedding space together. The combined representations are used to measure embedding distances between enzymes. And (3) the EC number prediction segment (Fig. 1c), which is responsible for determining the EC number of a query enzyme based on the projector and the combined representation of the query enzyme learned through contrastive learning. P-value EC number selection algorithm or Max-separation EC number selection algorithm are employed to predict EC numbers of query enzymes.

Fig. 1: Schematic illustration of the CLEAN-Contact framework.
figure 1

a Obtaining structure and sequence representations from contact map and amino acid sequence using ResNet50 and ESM2, respectively. b The contrastive learning segment. Sequence and structure representations are combined and projected into high-dimensional vectors using the projector. Positive samples are those with the same EC number as the anchor sample and negative samples are chosen from EC numbers with cluster centers close to the anchor. We perform contrastive learning to minimize distances between anchor and positive samples, and maximize distances between anchor and negative samples. c The EC number prediction segment. Cluster centers are computed for each EC number by averaging learned vectors within that EC number. Euclidean distances between the query enzyme’s vector and the cluster centers are calculated to predict the EC number of a query enzyme.

Full size image

Benchmark results

We conducted comprehensive evaluations of our proposed CLEAN-Contact framework, comparing it against five state-of-the-art EC number prediction models, CLEAN7, DeepECtransformer14, DeepEC4, ECPred15, and ProteInfer5. These models, along with the CLEAN-Contact, underwent testing on two independent test datasets. The first test dataset, New-3927 contains 392 enzyme sequences distributed over 177 different EC numbers (Supplementary Data 1). Predictive performance was assessed using four different metrics, Precision, Recall, F1-score, and Area Under Receiver Operating Characteristic Curve (AUROC). The EC numbers predicted by CLEAN-Contact and CLEAN were chosen using the P-value EC number selection algorithm with the same hyperparameters. The CLEAN-Contact achieved better performance. Specifically, CLEAN-Contact exhibited a 16.22% enhancement in Precision (0.652 vs. 0.561), a 9.04% improvement in Recall (0.555 vs. 0.509), a 12.30% increase in F1-score (0.566 vs. 0.504), and a 3.19% elevation in AUROC (0.777 vs. 0.753) over CLEAN (Fig. 2a and Supplementary Fig. 1a,b and Supplementary Fig. 2a). Conversely, ECPred and DeepEC recorded the lowest performance. The second test dataset, Price-1497 comprises 149 enzyme sequences distributed over 56 different EC numbers (Supplementary Data 2). Once more, CLEAN-Contact exhibited superior performance. Specifically, CLEAN-Contact showcased enhancements across various metrics compared to CLEAN, the second best performing model: a 16.95% improvement in Precision (0.621 vs. 0.531), an 18.20% increase in Recall (0.513 vs. 0.434), a 16.15% boost in F1-score (0.525 vs. 0.452), and a 5.44% elevation in AUROC (0.756 vs. 0.717; Fig. 2b and Supplementary Fig. 1c, d and Supplementary Fig. 2b). ECPred recorded the lowest performance measured by Recall and F1-score, while DeepEC recorded the lowest performance measured by Precision. Notably, CLEAN-Contact achieved a 2.0- to 2.5-fold improvement in Precision compared to DeepEC (0.238), ECPred (0.333), and ProteInfer (0.243), a 25.6-fold increase in Recall compared to ECPred (0.020), and a 13.8-fold improvement in F1-score compared to ECPred (0.038). Besides comparing CLEAN-Contact and CLEAN using the P-value EC number selection algorithm, we sought to ensure its comparative performance against CLEAN using the Max-separation EC number selection algorithm. We evaluated Precision, Recall, F1-score, and AUROC of both CLEAN-Contact and CLEAN on the two test datasets. Notably, CLEAN-Contact outperformed CLEAN by exhibiting an average improvement of 10.6% across the two test datasets (Supplementary Fig. 3).

Fig. 2: Assessment of predictive performance between CLEAN-Contact and baseline models.
figure 2

a, b Predictive performance between CLEAN-Contact and baseline models (CLEAN, DeepECtransformer, DeepEC, ECPred, and ProteInfer) measured by Precision, Recall, F1-score, and AUROC metrics on the New-392 and Price-149 test datasets. c, d Precision and recall of CLEAN-Contact and the second best performing model, CLEAN, on the merged test dataset, correlating with the frequency of occurrence of EC numbers in the training dataset. e, f Precision and recall of CLEAN-Contact and CLEAN on the merged dataset, correlating with the maximum sequence identity of proteins in the test dataset compared to the training dataset.

Full size image

To investigate the performance of CLEAN-Contact concerning understudied EC numbers, we merged the two test datasets and divided the merged test dataset based on the frequency of an EC number’s occurrence in the training dataset. Subsequently, we measured the Precision and Recall of both CLEAN-Contact and CLEAN on these divided test datasets. CLEAN-Contact demonstrated a 30.4% improvement (0.661 vs. 0.507) in Precision while achieving comparable performance against CLEAN when the EC number was rare in the training dataset (occurring more than 5 times but less than 11 times) and a 27.4% improvement (0.847 vs. 0.665) in Precision and a 21.4% improvement (0.693 vs. 0.571) in Recall compared to CLEAN when moderately infrequent (occurring more than 10 times but less than 51 times; Fig. 2c, d). However, when the EC number was extremely rare in the training dataset (occurring less than 6 times) or very common (occurring more than 100 times), the improvement of CLEAN-Contact over CLEAN was less significant (0.506 vs. 0.501 in Precision and 0.435 vs. 0.425 in Recall for EC numbers occurring less than 6 times, 0.731 vs. 0.669 in Precision and 0.575 vs. 0.525 in Recall for EC numbers occurring more than 50 times but less than 101 times, and 0.694 vs. 0.656 in Precision and 0.528 vs. 0.569 in Recall for EC numbers occurring more than 100 times; Fig. 2c, d). These findings underscore the significant enhancement in predictive performance achieved by integrating structural information into CLEAN-Contact.

Furthermore, we divided the merged test dataset based on the maximum sequence identity with the training dataset and evaluated the Precision and Recall of both CLEAN-Contact and CLEAN on these divided test datasets. When the sequence identity with the training dataset was very low (less than 30%), both models achieved comparable performance (Fig. 2e, f). However, as the maximum sequence identity ranged from 30% to 50%, CLEAN-Contact exhibited a 12.3% improvement in Precision (0.501 vs 0.446) and a 12.0% improvement in Recall (0.430 vs. 0.384) over CLEAN (Fig. 2e, f). As the maximum sequence identity increased to between 50% and 70%, CLEAN-Contact still maintained a 1.34% advantage in Precision (0.678 vs. 0.669) and a 2.32% advantage in Recall (0.617 vs. 0.603) over CLEAN (Fig. 2e, f). Remarkably, when the maximum sequence identity exceeded 70%, CLEAN-Contact showcased a 9.33% improvement over CLEAN (0.633 vs. 0.579) in Precision and a comparable performance in Recall (0.594 vs. 0.589; Fig. 2e, f).

Computational cost is another important factor in evaluating the performance of the classification model. We evaluated the computational cost of CLEAN-Contact and CLEAN, focusing on their inference steps. For CLEAN-Contact, this includes generating sequence representations using ESM-2, structure representations using ResNet-50, and predicting EC numbers of query enzymes using the contrastively learned model. CLEAN’s inference steps include obtaining representations through ESM-1b and making predictions. We quantified computational complexity using Giga Floating Operations (GFLOPs) and time consumption for each step. To ensure a fair comparison, we used the average protein sequence length from our test dataset (439 amino acids) as a benchmark, since the computational cost of ESM-1b, ESM-2, and ResNet-50 are input-size dependent. We excluded the cost of generating PDB structures for proteins lacking entries in the AlphaFold Protein Structure Database16. Our analysis revealed that CLEAN-Contact requires only an additional 0.1776 seconds per enzyme compared to CLEAN (Supplementary Table 1) while achieving significant performance improvement over CLEAN, scoring more than 20% improvement in several benchmark metrics.

Quantifying prediction confidence of CLEAN-Contact

We harnessed the Gaussian Mixture Model (GMM)17 to quantify the prediction confidence of CLEAN-Contact. Specifically, we randomly sampled 500 different EC numbers, followed by computing the distances between these EC numbers and the enzymes associated with these 500 EC numbers. The enzyme counts versus distances form a “same-EC” Gaussian distribution, representing the enzymes with correct EC numbers (Left peak in Supplementary Fig. 4a). Subsequently, we sampled negative enzymes that are not associated with these 500 EC numbers, and computed the distances between these EC numbers and the sampled negative enzymes. The negative enzyme counts versus distances forms a “different-EC” Gaussian distribution, representing the enzymes with incorrect EC numbers (Right peak in Supplementary Fig. 4a). We then employed a 2-component GMM to fit these two Gaussian distributions, with one component representing the “same-EC” Gaussian distribution while the other representing the “different-EC” Gaussian distribution. To determine the confidence, we started by computing the distance between the query enzyme and the predicted EC number. The density of the fitted GMM component corresponding to the “same-EC” distribution for this distance is used as prediction confidence. Following this, we assessed the performance of CLEAN-Contact across increasing cumulative confidence levels on the merged test dataset. The Precision and Recall of CLEAN-Contact showed improvement with higher cumulative confidence, consistently outperforming CLEAN across all cumulative confidence levels (Supplementary Fig. 4b, c).

Additionally, we employed the fitted GMM to address concerns about overprediction. Specifically, we restricted predictions to the 4th-level EC number only when the prediction confidence exceeds 0.5; otherwise, we predict the 3rd-level EC number. This adaptive prediction strategy mitigated overprediction issues by favoring the prediction of 3rd-level EC numbers at lower confidence levels (Supplementary Fig. 4d). Remarkably, when employing this adaptive prediction strategy, CLEAN-Contact yielded more true positives compared to exclusively predicting 4th-level EC numbers across all scenarios. Additionally, CLEAN-Contact consistently outperformed CLEAN in terms of predictive accuracy.

Discovery of unknown functions of enzymes in Prochlorococcus marinus MED4

We next aimed to uncover unknown enzyme functions within the proteome of Prochlorococcus marinus (P. marinus) MED4 (UniProt Proteome ID: UP000001026). P. marinus is a dominant photosynthetic organism in tropical and temperate open ocean ecosystems and is notable for being the smallest known photosynthetic organism18. The proteome of P. marinus MED4 comprises 1942 proteins, of which 583 had been annotated with at least one EC number in the UniProt database19, which encompasses a total of 488 distinct EC numbers (Supplementary Data 3).

We first employed both CLEAN-Contact and CLEAN to predict EC numbers for all 1942 proteins in the P. marinus MED4 proteome. Of the 488 annotated EC numbers, CLEAN-Contact correctly predicted 385, while CLEAN correctly predicted 379 (Fig. 3a and Supplementary Data 3). Both methods predicted 373 new EC numbers, with CLEAN-Contact independently predicting an additional 442 new EC numbers (Fig. 3a). CLEAN-Contact had higher overall prediction confidence compared to CLEAN, further confirming the better performance of CLEAN-Contact through integrating both protein structure and sequence information (Fig. 3b). Analysis of the first-level EC numbers predicted by CLEAN-Contact revealed that EC:2 comprised the most of predictions (30.2%), followed by EC:1 (21.5%) and EC:3 (21.3%), with the remaining first-level EC numbers accounting for 27% (Fig. 3c).

Fig. 3: Enzyme function prediction within the proteome of Prochlorococcus marinus MED4.
figure 3

a Comparison of EC numbers annotations for P. marinus MED4 proteome through three methods: manual annotation from UniProt (bottom) and computational prediction using CLEAN-Contact (left) and CLEAN (right). The overlapping regions indicate EC numbers shared between different methods. b Assessment of prediction confidence between CLEAN-Contact and CLEAN for the n=583 annotated enzymes. Box plot elements: The center lines represent the median prediction confidences. The upper and lower box limits represent upper and lower quartiles, respectively. Whiskers extend to the maximum and minimum prediction confidences. Individual points represent all prediction confidence values. c Distribution of first-level EC numbers predicted by CLEAN-Contact for 1212 unannotated and unreviewed enzymes. d Visualization of 38 enzymes with high-confidence predictions and their corresponding predicted first-level EC number.

Full size image

We next focused our attention on the predicted EC numbers for proteins lacking annotated EC numbers and in the “unreviewed” status, indicating they had not yet been manually annotated by experts. A total of 1212 proteins meet these criteria. To ensure prediction reliability, we applied strict confidence threshold. By considering only predictions with a confidence score exceeding 0.9, we identified 38 enzymes with a total of 36 predicted EC numbers (Fig. 3d and Supplementary Data 3). Notable examples include protein with UniProt ID of Q7V3C0, predicted as citrate synthase (EC:2.3.3.16) with 0.991 confidence, aligning with its protein name in the UniProt database, protein with UniProt ID of A8WIJ5, uncharacterized protein in the UniProt database, predicted as tetrahydromethanopterin S-methyltransferase (EC:2.1.1.86) with 0.996 confidence, and protein with UniProt ID of Q7V190, conserved hypothetical protein in the UniProt database, predicted to be 6-carboxyhexanoate–CoA ligase (EC:6.2.1.14) with 0.972 confidence (Fig. 3d and Supplementary Data 3). Together, these results demonstrated CLEAN-Contact’s potential for identifying unknown enzyme functions, particularly uncharacterized or hypothetical proteins.

Interpreting CLEAN-Contact

We investigated the impact of various representation components, specifically comparing sequence representations derived from ESM-2 against those derived from ESM-1b, along with including structure representations. We observed that replacing ESM-1b with ESM-2, without incorporating structure representations, led to a marginal 1.39% average performance improvement across the two test datasets (Fig. 4). However, integrating structure representations while retaining ESM-1b yielded a substantial 5.76% average performance increase across the two test datasets (Fig. 4). Moreover, replacing ESM-1b with ESM-2 and including structure representations resulted in a 6.13% average performance improvement (Fig. 4). Notably, utilizing solely structure representations as the model input yielded the poorest performance. We attributed this outcome to the fact that contact maps only offer information about residue contacts within the protein structure, lacking crucial details about the amino acids.

Fig. 4: Ablation results.
figure 4

We conducted a comparative analysis of several model variations, including our proposed CLEAN-Contact (ESM2+Contact), CLEAN-Contact without structure representation (ESM2), CLEAN-Contact with ESM-1b instead of ESM-2 (ESM1b+Contact), the original CLEAN (ESM1b), and a model with solely structure representation devoid of ESM-2 or ESM-1b generated sequence representation (Contact). a, Evaluation of predictive performance metrics (Precision, Recall, F-1 score, and AUROC) across different models on the New-392 test dataset. b, Evaluation of predictive performance metrics (Precision, Recall, F-1 score, and AUROC) across different models on the Price-149 test dataset.

Full size image

To find out how different computer vision models can affect the performance of CLEAN-Contact, we trained and evaluated four CLEAN-Contact variants employing different CNNs: three ResNet-based models9 (ResNet-18, ResNet-50, and ResNet-101) and one vision transformer-based model (SwinV2-B20). While ResNet-18 has the lowest computational cost, it also demonstrates the lowest performance in ImageNet classification tasks21 (Supplementary Table 2). ResNet-50, ResNet-101, and SwinV2-B exhibit comparable performance in these tasks, while the number of parameters ranges from 25.6M (ResNet-50) to 87.9M (SwinV2-B) (Supplementary Table 2). Our experiments on the merged test dataset revealed that ResNet-based models in CLEAN-Contact showed similar performance, with ResNet-50 slightly outperforming others (Supplementary Table 3). Interestingly, SwinV2-B variant of CLEAN-Contact underperformed compared to the ResNet-based models (Supplementary Table 3). These findings suggested that ResNet-50 offers the optimal balance, maximizing the extraction of useful information from protein contact maps while maintaining computational efficiency.

To study the impact of sample quantities for contrastive learning on the performance of CLEAN-Contact, we conducted a series of experiments with different numbers of anchor, positive, and negative samples. We trained models with 1, 2, and 4 samples for each sample type and adhered to the constraints imposed by the triplet margin loss function. The triplet margin loss function requires an equal number of positive and negative samples. Additionally, it requires that the number of positive samples must be either one, equal to the number of anchor samples, or greater than the number of anchor samples. We observed an inverse relationship between sample quantity and model performance. Notably, increasing the number of positive and negative samples led to a more significant decrease in performance compared to increasing the number of anchor samples alone (Supplementary Table 4).

Discussion

In this work, we introduce a enzyme function prediction framework based on contrastive learning, which integrates both enzyme amino acid sequence and structural data to predict EC numbers. Our proposed CLEAN-Contact framework harnesses the power of ESM-2, a pretrained protein language model responsible for encoding amino acid sequences, and ResNet, a convolutional neural network utilized for encoding contact maps. Through comprehensive evaluations on diverse test datasets, we have meticulously assessed the CLEAN-Contact framework’s performance. In addition to benchmark analysis, we leveraged CLEAN-Contact to discover previously unknown enzyme functions in Prochlorococcus marinus MED4. Specifically, CLEAN-Contact predicted enzyme functions with high confidence for 38 proteins that had not been manually annotated and reviewed by experts. Our extensive comparisons and detailed analyses firmly established that the fusion of structural and sequence information substantially enhances the predictive performance of models used for enzyme functional annotation prediction. As a result, CLEAN-Contact represents a significant step forward in the field of enzyme annotation, providing a robust framework for enzyme function prediction.

However, our work does come with certain limitations. First, our utilization of structure information relies on contact maps, 2D matrix representations, rather than utilizing the full 3D protein structures of enzymes. One potential solution to overcome this limitation involves the incorporation of 3D interaction sequences (3Di)22 into the framework. These sequences contain valuable information regarding geometric conformations between residues. Another possible way to enhance CLEAN-Contact involves considering EC numbers as hierarchical labels. This approach entails employing hierarchical losses, such as hierarchical contrastive loss23 or exploring other hierarchical classification loss methodologies24,25.

Even though our focus in this work is solely on predicting enzyme functional annotations, we firmly believe that our proposed CLEAN-Contact framework has broader applications beyond this domain. A promising future direction could involve extending our model to predict general protein functional annotations, such as Gene Ontology (GO) numbers26 and FunCat categories27. This expansion would significantly broaden the application and utility of our model.

Methods

Description of Dataset

The enzyme’s amino acid sequences in the training dataset were retrieved from Swiss-Prot28 (accessed April 2022). Sequences lacking structures available in the AlphaFold Protein Structure Database16 (https://alphafold.ebi.ac.uk/) were filtered out from the training dataset. The processed training dataset comprises 224,742 amino acid sequences, covering 5197 EC numbers. We obtained PDB structures for the proteins in the processed training dataset from the AlphaFold Protein Structure Database. Test datasets, New-392 and Price-149, consist of 392 and 149 amino acid sequences, respectively, distributed across 177 and 56 EC numbers, as provided by7 (Supplementary Data 1 and 2). Within the New-392 test dataset, 8 enzymes, and within the Price-149 test dataset, 28 enzymes lacked readily available structures from the AlphaFold Protein Structure Database (Supplementary Data 1 and 2). To address this, we employed all 5 models within AlphaFold23 to generate protein structures for these 36 enzymes. From the 5 generated protein structures for each enzyme, we selected the one with the highest confidence to derive contact maps. Notably, enzymes where an ‘X’ appeared within the amino acid sequence rendered AlphaFold2 unable to assess structure confidence. In such cases, we utilized the protein structures generated from “model_1”. The case study dataset, comprising 1,942 proteins, was obtained from the UniProt database (UniProt proteome ID: UP000001026, accessed September 2024). Of 1942 proteins, 583 were annotated with at least one EC number, while 1212 were neither annotated nor reviewed by experts. There is no overlapping between the proteins in the case study dataset and those in the training dataset. The contact map was defined as the distance between Cβ − Cβ with a threshold of 8 Å. The contact map was then expanded into three channels with identical values for each channel. Contact maps were calculated using biotite 0.38.0 (https://www.biotite-python.org/), Scipy 1.11.4 (https://scipy.org/), and Biopython 1.81 (https://biopython.org/).

The maximum sequence identity between the test dataset and the training dataset was calculated using BLASTp 2.15.029. A BLAST database was built (makeblastdb -in split100_reduced.fasta -dbtype prot) on the training dataset before performing BLASTp search (blastp -query test.fasta -db split100_reduced.fasta -num_threads 32 -outfmt 5 -out test.xml) using the test dataset as the query database and the training dataset as the target database. The sequence identity was defined as HSP_identity / HSP_align_length, and the maximum sequence identity was selected from all hits for each protein in the query database.

Description of Framework

As shown in Fig. 1, our framework consists of two components: the contrastive learning segment and the EC number prediction segment.

We initiate our approach by obtaining contact maps \(C\in {{\mathbb{R}}}^{{n}_{r}\times {n}_{r}}\) from protein structures, where nr denotes the number of residues in a protein. To expand C into a three-channel matrix \({C}_{3}\in {{\mathbb{R}}}^{{n}_{r}\times {n}_{r}\times 3}\), each channel holds identical values. Utilizing the ResNet509 model pretrained on ImageNet21, we extract high-dimensional structure representations from contact maps:

$$c={{{\mathcal{R}}}}({C}_{3}),$$
(1)

where \({{{\mathcal{R}}}}\) is the pretrained ResNet50 without its classification layer, and \(c\in {{\mathbb{R}}}^{{d}_{c}}\) is the structure representation, with dc as its dimension. The dimension of the obtained structure representation dc was 2, 048.

Recognizing that contact maps alone lack vital amino acid information, we leverage the ESM-2 model8 with 36 layers and 3B parameters to derive sequence representations from proteins’ amino acid sequence:

$$a={{{\mathcal{E}}}}({s}_{aa}),$$
(2)

where \({{{\mathcal{E}}}}\) is the pretrained ESM-2 model, saa is the protein’s amino acid sequence, and \(a\in {{\mathbb{R}}}^{{d}_{a}}\) is the sequence representation, with da as its dimension. The dimension of the derived sequence representation da was 2, 560.

To fuse the sequence and structure representations into a vector \(z\in {{\mathbb{R}}}^{{d}_{z}}\), we employ a projector \({{{{\mathcal{F}}}}}_{{{\Psi }}}(\cdot )\). The projector contains three levels of linear layers, each followed by layer normalization30:

$$z = {{{{\mathcal{F}}}}}_{{{\Psi }}}(a,c),\\ = {W}_{3}\left.\right({{\mbox{LN}}}_{2}\left({W}_{2}\left({{\mbox{LN}}}_{1}\left({W}_{1,a}a+{W}_{1,c}c\right)\right)\right),$$
(3)

where LNi is the ith layer normalization, \({W}_{1,a}\in {{\mathbb{R}}}^{{d}_{1}\times {d}_{a}}\), \({W}_{1,c}\in {{\mathbb{R}}}^{{d}_{1}\times {d}_{c}}\), \({W}_{2}\in {{\mathbb{R}}}^{{d}_{2}\times {d}_{1}}\) and \({W}_{3}\in {{\mathbb{R}}}^{{d}_{z}\times {d}_{2}}\) are the weights of the linear layers, while Ψ is the projector’s trainable parameters.

Subsequently, we compute representations for EC numbers by concatenating the sequence and structure representations of proteins under a specific EC number and averaging these concatenated representations:

$${r}_{{\mbox{EC}},i}=\frac{1}{| {{\mbox{EC}}}_{i}| } {\sum}_{j\in {{\mbox{EC}}}_{i}}\left(\,{\mbox{Concat}}\,({a}_{j},{c}_{j})\right),$$
(4)

where rEC,i is the representation of the ith EC number, ECi is the set of enzymes associated with the ith EC number, ∣ECi∣ is the set’s cardiality, and aj and cj are the sequence and structure representations, respectively, of the jth enzyme under the ith EC number.

Further, we compute the distance map between the representations of EC numbers utilizing Euclidean distance:

$$d({{\mbox{EC}}}_{i},{{\mbox{EC}}}_{j}) = | | {z}_{{\mbox{EC}},i}-{z}_{{\mbox{EC}},j}| {| }_{2},\\ = | | {{{\mathcal{F}}}}({a}_{{\mbox{EC}},i},{c}_{{\mbox{EC}},i})-{{{\mathcal{F}}}}({a}_{{\mbox{EC}},j},{c}_{{\mbox{EC}},j})| {| }_{2},$$
(5)

where d(ECi, ECj) is the Euclidean distance between the projected vectors of the ith and jth EC numbers.

During the training phase, we select anchor samples o for each EC number and positive samples p sharing the same EC number as o. For negative samples, we initially choose negative EC numbers with representations that are close to the anchor’s EC number representation in Euclidean distance, then select negative samples from these negative EC numbers. We employ the triplet margin loss31 for contrastive learning:

$${{{\mathcal{L}}}}=\max (| | {z}_{o}-{z}_{p}| {| }_{2}-| | {z}_{o}-{z}_{n}| {| }_{2}+\epsilon ,0),$$
(6)

where ϵ is the margin for triplet loss (sets as 1 for all experiments), zo is the projected vector for the anchor sample, zp is the projected vector for the positive sample, and zn is the projected vector for the negative sample.

For the EC number prediction phase, we utilize the contrastively trained projector \({{{\mathcal{F}}}}\) to obtain vectors for enzymes from both the training dataset and test dataset. Subsequently. we compute cluster centers of EC numbers present in the training dataset by averaging the vectors of enzymes associated with each EC number. We then compute the Euclidean distance between the vectors of query enzymes in the test set and vectors of EC numbers. Finally, we predict potential EC numbers utilizing both the P-value and Max-separation EC number prediction algorithm as mentioned in Yu et al.7. (See Section 4.3 and Section 4.4). PyTorch 2.1.1 (https://pytorch.org/), torchvision 0.16.1 (https://pytorch.org/vision/), fair-esm 2.0.0 (https://github.com/facebookresearch/esm), and PyTorch-CUDA 12.1 (https://pytorch.org/) were used to implement the whole framework.

EC number selection using P-value

The P-value EC number selection algorithm, as proposed by Yu et al.7, involves several key steps. Initially, a P value was selected, followed by the random sampling of n enzymes from the training dataset, setting a selection threshold δ = P × n. However, instead of uniformly sampling n enzymes, we assign a higher weight to an enzyme whose associated EC numbers contain a smaller number of enzymes:

$${p}_{e}=\frac{1/\max (| {{\mbox{EC}}}_{e}| )}{{\sum }_{i\in S}1/max(| {{\mbox{EC}}}_{i})},$$
(7)

where pe is the assigned probability of enzyme e, ECe are all EC number sets including enzyme e, \(\max (| {{\mbox{EC}}}_{e}| )\) is the maximum cardinality among all EC number sets involving enzyme e, and S is the entire set of enzymes.

Moving forward, we compute the distance map between the randomly sampled n enzymes and EC numbers in the training dataset using vectors encoded by the trained projector \({{{\mathcal{F}}}}\):

$$d({{\mbox{EC}}}_{i},{e}_{j}) = \, | | {z}_{{\mbox{EC}},i}-{z}_{e,j}| {| }_{2},\\ = \, | | {{{\mathcal{F}}}}({a}_{{\mbox{EC}},i},{c}_{{\mbox{EC}},i})-{{{\mathcal{F}}}}({a}_{e,j},{c}_{e,j})| {| }_{2},$$
(8)

where ej is the jth enzyme in the randomly chosen n enzymes, a is the sequence representation, and c is the structure representation. Subsequently, with respect to each EC number, we obtain a set of distances \({{{\mathcal{D}}}}(\,{\mbox{EC}})=\left\{d(\,{\mbox{EC}},{e}_{1}),d({\mbox{EC}},{e}_{2}),...,d({\mbox{EC}}\,,{e}_{n-1})\right\}\), sorted in ascending order.

The next step involves identifying the 10 closest cluster centers of EC numbers to the query enzyme and the corresponding distances between the query enzyme’s projected vector to the cluster centers. These 10 EC numbers were denoted as ECk, with corresponding distances labeled as dk, where k ∈ [1, 10]. EC1 represents the EC number with the closest distance d1 to the query enzyme. We retain the first EC number, which has the smallest distance to the query enzyme, as a prediction result. Subsequently, we iterate over the remaining 9 EC numbers. For each EC number ECk, we find the index u in \({{{\mathcal{D}}}}({{\mbox{EC}}}_{k})\) where dk should be inserted such that:

$$d({{\mbox{EC}}}_{k},{e}_{u-1}) \, < \, {d}_{k}\le d({{\mbox{EC}}}_{k},{e}_{u+1}).$$
(9)

We retain ECk as a prediction result if the insertion index is smaller than the threshold δ:

$$u\le \delta .$$
(10)

EC number selection using Max-separation

The Max-separation EC number selection algorithm, as introduced by Yu et al.7, differs from the P-value algorithm in that it does not need necessitate the selection of hyperparameters P and n.

The procedure begins by sorting the distance map between the projected vector of query enzyme and the cluster centers of EC numbers within the training dataset in ascending order. Next, the algorithm selects ten EC numbers ECk with the smallest distances dk, k ∈ [1, 10] to the query enzyme, computing their average distances:

$$\gamma =\frac{1}{10} {\sum}_{k=1}^{10}{d}_{k}.$$
(11)

Following this, the algorithm computes the differences between each distance and the average:

$${q}_{k}=| {d}_{k}-\gamma | ,k\in [1,10].$$
(12)

Subsequently, the algorithm computes the differences between adjacent items and computes their average:

$${g}_{k} = | {q}_{k}-{q}_{k-1}| ,k\in [2,10],\\ \bar{g} = \frac{1}{9} {\sum}_{i=2}^{10}{g}_{i}.$$
(13)

The algorithm proceeds to select the index i for which \({g}_{i} \, > \, \bar{g}\) and uses ECi as the prediction result. In case where no index i satisfies the condition \({g}_{i} \, > \, \bar{g}\), EC1 is used as the prediction result.

Quantification of prediction confidence

We randomly sampled 500 different EC numbers from the training dataset, followed by computing the distances between these 500 EC numbers and the enzymes associated with these 500 EC numbers using Eq. (8). The distribution of enzyme counts versus distances forms the “same-EC” Gaussian distribution (Left peak in Supplementary Fig. 4a). Subsequently, we sampled negative enzymes using the negative enzyme selection strategy mentioned in Section 4.2 and computed distances between the 500 EC numbers and the sampled negative enzymes using Eq. (8). The distribution of negative enzyme counts versus distances forms the “different-EC” Gaussian distribution (Right peak in Supplementary Fig. 4a). The random sampling was performed for 10 times. One 2-component Gaussian Mixture Model (GMM) provided by Scikit-learn32 was fitted each time, with one component corresponding to the “same-EC” distribution while the other corresponding to the “different-EC” distribution. Supplementary Fig. 4a shows distances between all randomly sampled EC numbers and their associated enzymes and their sampled negative enzymes during the 10 sampling processes. The random package provided by Python 3.10.13 (https://docs.python.org/release/3.10.13/library/random.html) was used to sample EC numbers and negative enzymes.

To quantify prediction confidence, we started by computing the distance between the query enzyme and the predicted EC number using Eq. (8). Subsequently, we computed density of the fitted GMM component corresponding to the “same-EC” distribution for this distance as the prediction confidence. Prediction confidence for each enzyme provided in Fig. 3 and Supplementary Fig. 4 was the mean of 10 densities of the fitted GMM “same-EC” component.

Statistics and reproducibility

Statistical analyses were performed in Python 3.10.13 (https://www.python.org/). Numpy 1.26.2 (https://numpy.org/), Pandas 2.1.1 (https://pandas.pydata.org/), and Scikit-learn32 were used for statistical analyses. Matplotlib 3.8.0 (https://matplotlib.org/), Seaborn 0.13.2 (https://seaborn.pydata.org/), and matplotlib_venn (https://github.com/konstantint/matplotlib-venn) were used for visualizing results. Details of the sample size, number of replicates, and statistical analyses for each experiment and case study are listed in the respective parts of the Results and Methods sections.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.