Exotic spin-Hall effect in non-Hermitian optical systems

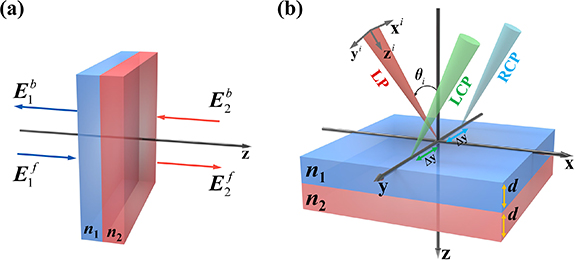
In general, a PT-symmetric system is composed of gain and loss layers of equal thickness d whose refractive indices satisfy ${n_1} = n_2^ *$ (figure 1). Considering a light beam incident on the PT-symmetric system placed in air, we define (x, y, z) and (x^a, y^a, z^a) as the laboratory and local coordinate systems, respectively. Here, the superscripts a = {i,r} denotes the incidence and reflection, respectively. Based on the angular spectrum theory, the electric field of the light beam can be written as [35],

$$\begin{equation}{{\boldsymbol{E}}^a}\left({{\boldsymbol{r}}^{\,a}}\right) = \int {{{\text{d}}^2}{\boldsymbol{k}}_ \bot ^a{\boldsymbol{ }}{e^{i{{\boldsymbol{k}}^a} \cdot {{\boldsymbol{r}}^{\,a}}}}\sum\limits_{\sigma {\text{ = + ,}} - } {U_\sigma ^a\left( {{{\boldsymbol{k}}^a}} \right){\boldsymbol{\hat V}}_\sigma ^{\,a}} } ,\end{equation} \tag{ 1 }$$

Zoom In Zoom Out Reset image size

where ${{\boldsymbol{k}}^a} \cdot {{\boldsymbol{r}}^{\,a}} = {\boldsymbol{k}}_ \bot ^a \cdot {\boldsymbol{r}}_ \bot ^{\,a} + k_z^a{z^{\,a}}$ with $k_z^a = \sqrt {{{({k^a})}^2} - {{(k_ \bot ^a)}^2}}$, ${{\boldsymbol{k}}^a}$ and ${{\boldsymbol{r}}^{\,a}}$ are the wave vector and position vector in local coordinate system, respectively. ${\boldsymbol{\hat V}}_\sigma ^a = ({{\boldsymbol{\hat x}}^a} + \sigma i{{\boldsymbol{\hat y}}^a})/\sqrt 2$ denotes unit vectors of LCP (+) and RCP (−), and $U_\sigma ^a \left( {{{\boldsymbol{k}}^a}} \right)$ represents the transverse field of the beam in k-space.

We establish a transfer matrix to connect the incident beam to the reflected beam, namely [35],

$$\begin{equation}\left[ {\begin{array}{*{20}{c}} {U_ + ^r\left({{\boldsymbol{k}}^r}\right)} \\ {U_ - ^r\left({{\boldsymbol{k}}^r}\right)} \end{array}} \right] = {{\boldsymbol{M}}^{\left(r\right)}}\left[ {\begin{array}{*{20}{c}} {U_ + ^i\left({{\boldsymbol{k}}^i}\right)} \\ {U_ - ^i\left({{\boldsymbol{k}}^i}\right)} \end{array}} \right] \approx \left[ {\begin{array}{*{20}{c}} {{r_{ + + }}\left({{\boldsymbol{k}}_{||}}\right)}&{{r_{ + - }}\left({{\boldsymbol{k}}_{||}}\right){e^{ - i\Phi _{\text{B}}^{{\text{abn}}}}}} \\ {{r_{ - + }}\left({{\boldsymbol{k}}_{||}}\right){e^{i\Phi _B^{abn}}}}&{{r_{ - - }}\left({{\boldsymbol{k}}_{||}}\right)} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {U_ + ^i\left({{\boldsymbol{k}}^i}\right)} \\ {U_ - ^i\left({{\boldsymbol{k}}^i}\right)} \end{array}} \right].\end{equation} \tag{ 2 }$$

Here,

$$\begin{align} {r_{ + + }}\left({{\boldsymbol{k}}_\parallel }\right) & = {r_{ - - }}\left({{\boldsymbol{k}}_\parallel }\right) = \frac{1}{2}\left[ {{r_p}\left({{\boldsymbol{k}}_\parallel }\right) + {r_s}\left({{\boldsymbol{k}}_\parallel }\right)} \right], \nonumber\\ {r_{ + - }}\left({{\boldsymbol{k}}_\parallel }\right) & = {r_{ - + }}\left({{\boldsymbol{k}}_\parallel }\right) = \frac{1}{2}\left[ {{r_p}\left({{\boldsymbol{k}}_\parallel }\right) - {r_s}\left({{\boldsymbol{k}}_\parallel }\right)} \right] \end{align} \tag{ 3 }$$

represent the Fresnel reflection coefficient of the circular polarization basis with tangential wave vector k_|| defined in the laboratory coordinate system. $\Phi _{{\text{PB}}}^{{\text{abn}}} \approx 2{\phi _{{\boldsymbol{ k}}}}\cos {\theta _i}$ is a momentum-dependent Pancharatnam–Berry phase [35–39]. ${\theta _i}$ is the incident angle of the light beam, and ${\phi _{{\boldsymbol{ k}}}} = {\tan ^{ - 1}}({k_y}/{k_x})$ is the azimuthal angle of the incident plane of an any noncentral plane wave, while ${k_x} = k_x^r\cos {\theta _r} + k_z^r\sin {\theta _r}$ and ${k_y} = k_y^r$ are the transverse wave vector components of an arbitrary plane wave in laboratory coordinates. Here, ${r_p}({{\boldsymbol{k}}_\parallel })$ and ${r_s}({{\boldsymbol{k}}_\parallel })$ are the reflection coefficients of the p- and s-polarized plane waves within the beam, respectively. Performing a Fourier transform on the incident field ${\boldsymbol{E}}_ + ^i(r_ \bot ^i)$ to obtain its angular spectrum $U_ \pm ^i({{\boldsymbol{k}}^i})$, we substitute $U_ \pm ^i({{\boldsymbol{k}}^i})$ into equation (2) to get $U_ \pm ^r({{\boldsymbol{k}}^r})$, then the real fields obtained by putting $U_ \pm ^r({{\boldsymbol{k}}^r})$into equation (1) as,

$$\begin{equation}\begin{gathered} E_{ + + }^r\left({\boldsymbol{r}}_ \bot ^r\right) = \int {{{\text{d}}^2}} {\boldsymbol{k}}_ \bot ^r{e^{i{{\boldsymbol{k}}^r} \cdot {{\boldsymbol{r}}^r}}}{r_{ + + }}\left({{\boldsymbol{k}}_\parallel }\right)U_ + ^i\left({{\boldsymbol{k}}^i}\right) \hfill \\ E_{ - + }^r\left({\boldsymbol{r}}_ \bot ^r\right) = \int {{{\text{d}}^2}} {\boldsymbol{k}}_ \bot ^r{e^{i{{\boldsymbol{k}}^r} \cdot {{\boldsymbol{r}}^r}}}{r_{ - + }}\left({{\boldsymbol{k}}_\parallel }\right){e^{i\Phi _{\text{B}}^{{\text{abn}}}\left({{\boldsymbol{k}}^r}\right)}}U_ + ^i\left({{\boldsymbol{k}}^i}\right) \hfill \\ \end{gathered} .\end{equation} \tag{ 4 }$$

The above two equations represent the spin-maintained normal mode and spin-reversed abnormal mode, respectively. Finally, with a complete understanding of the electric field distribution of the reflected beam, we can use the following formula to calculate the spin-Hall shift of the beam:

$$\begin{equation}\begin{gathered} \Delta {y_{\alpha \beta }} = \frac{{\iint {{y^r}{{\left| {E_{\alpha \beta }^r} \right|}^2}{\text{d}}{x^r}{\text{d}}{y^r}}}}{{\iint {{{\left| {E_{\alpha \beta }^r} \right|}^2}{\text{d}}{x^r}{\text{d}}{y^r}}}}, \hfill \\ \Delta {x_{\alpha \beta }} = \frac{{\iint {{x^r}{{\left| {E_{\alpha \beta }^r} \right|}^2}{\text{d}}{x^r}{\text{d}}{y^r}}}}{{\iint {{{\left| {E_{\alpha \beta }^r} \right|}^2}{\text{d}}{x^r}{\text{d}}{y^r}}}} \hfill \\ \end{gathered} \end{equation} \tag{ 5 }$$

where $\alpha ,\beta \in \left\{ { + , - } \right\}$.

The scattering of a beam in the PT-symmetric optical system can be described by the scattering matrix S, which relates the output electric field ($E_1^b$, $E_2^f$) to the input one ($E_1^f$, $E_2^b$) (figure 1(a)). Two different scattering matrices with distinct sets of eigenvalues can be defined by the permutation of the outgoing waves, leading to apparent symmetry breaking. These two matrices are ${S_t} = \left[ {\begin{array}{*{20}{c}} t&{{r^f}} \\ {{r^b}}&t \end{array}} \right]$ and ${S_r} = \left[ {\begin{array}{*{20}{c}} {{r^f}}&t \\ t&{{r^b}} \end{array}} \right]$, where $\left[ {\begin{array}{*{20}{c}} {E_1^b} \\ {E_2^f} \end{array}} \right] = {S_t}\left[ {\begin{array}{*{20}{c}} {E_2^b} \\ {E_1^f} \end{array}} \right] \equiv \left[ {\begin{array}{*{20}{c}} t&{{r^f}} \\ {{r^b}}&t \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {E_2^b} \\ {E_1^f} \end{array}} \right]$ and ${S_r} = {S_t}{\sigma _x}$, ${\sigma _x} = \left[ {\begin{array}{*{20}{c}} 0&1 \\ 1&0 \end{array}} \right]$ is the Pauli matrix [40–43]. Here, f (b) denotes the propagation of the beam in the forward (backward) direction along the z-axis, t represents the transmission coefficient (note that ${t^f} = {t^b}$), and ${r^{f(b)}}$ signifies the reflection coefficient. The Fresnel coefficients can be calculated with the transfer-matrix method [44]. Although both definitions of the scattering matrix are widely used, it is obvious that the two definitions of S_r and S_t have different eigenvalues. We provide a detailed analysis of the EPs generated by the scattering matrix S_t in this paper. The eigenvalues of S_t are denoted as ${\psi _{1,2}} = t \pm \sqrt {{r^f}{r^b}}$. According to the generalized conservation relation [31, 45], we have $|T - 1| = \sqrt {{r^f}{r^{{f^ * }}}{r^b}{r^{{b^ * }}}}$, where $T = t{t^*}$ represents the transmittance. When $T < 1$, $\left| {{\psi _1}} \right| = \left| {{\psi _2}} \right|$, the system is in the exact PT-symmetric phase. When $T > 1$, $\left| {{\psi _1}} \right| \ne \left| {{\psi _2}} \right|$, the system exhibits a symmetry-breaking phase. Especially, if $T = 1$, ${r^f}$ or ${r^b} = 0$, the two eigenvalues coalesce into the same value, denoted as an EP.

We utilize the eigenvalues of the scattering matrix S_t to investigate the formation conditions and evolution of EPs in PT-symmetric systems. Initially, we select several representative refractive indices that adequately demonstrate the various scenarios in which EPs may occur. To illustrate the variation of EPs with changes in system parameters, the evolution curves of the eigenvalues corresponding to p-polarized (the first column) and s-polarized (the second column) waves against the incident angle are plotted separately (figure 2). For the system with a real part of the refractive index n_R = 1.5 and an imaginary part of the refractive index n_I = 0.5040, the system undergoes a transition from a PT-symmetric phase to a symmetry-breaking phase for both p-polarized and s-polarized incident beams. It returns to the PT-symmetric phase as the incident angle is further increased. In this process, two eigenvalues are merged for both polarizations, corresponding to the two EPs generated (figures 2(a) and (b)). Changing the refractive index to n_R= 3 and n_I = 0.5040, the p-polarized wave still follows a similar symmetry-breaking pattern as in figure 2(a) and forms two EPs again (figure 2(c)). However, for the s-polarized wave, even under the same refractive index conditions, it maintains a strictly symmetric phase, indicating that no EPs appear for this specific refractive index configuration (figure 2(d)). Nevertheless, under the refractive index setting of n_R= 3 and n_I = 0.7508, the system directly transitions from a symmetry-breaking phase to a strictly symmetric phase (figures 2(e) and (f)). During this process, only one EP appears for each of the p-polarized and s-polarized wave, demonstrating that small variations in the refractive index can lead to significant changes in the distribution and number of EPs. Furthermore, other system parameters, such as the thickness d, also have a significant impact on the symmetry of the PT-symmetric system.

Zoom In Zoom Out Reset image size

It is clear from the above discussions that the properties of EPs depend on the refractive index of the materials that make up the PT system, which directly influences the reflection coefficients. To better understand this relationship, figure 3 displays |r_p| (the first column) and |r_s| (the second column) for the specific refractive index values used in figure 2. As depicted by the EPs in figure 2, at these specific incident angles, the corresponding |r_p| and |r_s| values are both zero, marking the exact location of the EPs. Moreover, by analyzing the Fresnel coefficients, we can not only confirm the existence of EPs, but also determine the incident direction of the beam. Particularly in PT-symmetric systems, due to the symmetry characteristics of the loss layer and the gain layer, beams exhibit distinct phenomena when entering from each side. Therefore, the accurate determination of the incident direction corresponding to the EPs is crucial. Specifically, in figures 3(a) and (b), where $|r_p^f| = 0$, it indicates that the exotic phenomena associated with EPs can only be observed as the beam is incident from the forward direction of the material (from the loss layer). Conversely, in the scenario depicted in figure 3(c), where $|r_p^b| = 0$, it suggests that the beam must enter the material from the backward direction (i.e. from the gain layer). Also, both |r_p| and |r_s| in figure 3(d) have no zeros which implies that there is no EP, whereas figures 3(e) and (f) have one zero for |r_p| and |r_s| respectively, which correlates with the EPs in figures 2(e) and (f). This series of analyses offers an alternative perspective for effectively identifying and exploring EPs in non-Hermitian optical systems.

Zoom In Zoom Out Reset image size

After knowing the generation regularity of EPs in PT-symmetric systems, we can quickly find the distribution of EPs at different refractive index conditions. To further explore the SHE near the EPs, we now investigate the optical properties near the EPs through a series of full-wave calculations.

Assuming that the incident beam is a p-polarized Gaussian beam composed of the LCP and RCP components of equal intensity, we have $U_ + ^i({{\boldsymbol{k}}^i}) = U_ - ^i({{\boldsymbol{k}}^i}) = \exp \left[ { - {{(k_ \bot ^i{w_0})}^2}/4} \right]$, where w₀ is half-width of the beam waist. Then, substituting these initial conditions into equations (1) and (2), we get the LCP and RCP components in the reflected beam [13]:

$$\begin{align}\begin{array}{*{20}{l}} {E_ + ^r\left({\boldsymbol{r}}_ \bot ^r\right) = \int {{{\text{d}}^2}} {\boldsymbol{k}}_ \bot ^r{e^{i{{\boldsymbol{k}}^r} \cdot {{\boldsymbol{r}}^r}}}\left[ {{r_{ + + }}\left({{\boldsymbol{k}}_\parallel }\right) + {r_{ + - }}\left({{\boldsymbol{k}}_\parallel }\right){e^{ - i\Phi _{\text{B}}^{{\text{abn}}}\left({{\boldsymbol{k}}^r}\right)}}} \right]U_ + ^i\left({{\boldsymbol{k}}^i}\right) = E_{ + + }^r\left({\boldsymbol{r}}_ \bot ^r\right) + E_{ + - }^r\left({\boldsymbol{r}}_ \bot ^r\right)} \\ {E_ - ^r\left({\boldsymbol{r}}_ \bot ^r\right) = \int {{{\text{d}}^2}} {\boldsymbol{k}}_ \bot ^r{e^{i{{\boldsymbol{k}}^r} \cdot {{\boldsymbol{r}}^r}}}\left[ {{r_{ - - }}\left({{\boldsymbol{k}}_\parallel }\right) + {r_{ - + }}\left({{\boldsymbol{k}}_\parallel }\right){e^{i\Phi _{\text{B}}^{{\text{abn}}}\left({{\boldsymbol{k}}^r}\right)}}} \right]U_ + ^i\left({{\boldsymbol{k}}^i}\right) = E_{ - + }^r\left({\boldsymbol{r}}_ \bot ^r\right) + E_{ - - }^r\left({\boldsymbol{r}}_ \bot ^r\right)} \end{array}.\end{align} \tag{ 6 }$$

Equation (6) indicates that $E_ + ^r({\boldsymbol{r}}_ \bot ^r)$ and $E_ - ^r({\boldsymbol{r}}_ \bot ^r)$ consist of a spin-maintained normal mode and a spin-reversed abnormal mode, whose shifts can be obtained by putting the equation (6) into the equation (5).

By changing the parameters of the PT-symmetric system, a variety of intensity patterns can be obtained. Variations in the refractive index of the system may result in complex patterns exhibiting the rotation of the reflected beam at the EP, as shown in figure 4. Furthermore, by altering the polarization state of the incident beam, such as setting it to elliptical polarization, it is possible to adjust the weights of the normal and abnormal modes (as in equation (6)), thereby controlling the light-intensity distribution and the SHE. In fact, we can also alter the parameters of the PT-symmetric system so that the position of the EP appears at any incident angle, thereby controlling the SHE of light. Conversely, since the intensity distribution of the reflected beam in the PT-symmetric system varies with the refractive indices (n_R and n_I), we can locate the EP through the SHE.

Zoom In Zoom Out Reset image size

We select several particular distributions of light patterns to analyze in detail, which exhibit exotic SHE different from the Brewster effects. Firstly, we analyze the behaviors of p-polarized light incident from the forward direction in the PT-symmetric system. Figure 4(a) illustrates the variations of ${\left| {E_ + ^r({\boldsymbol{r}}_ \bot ^r)} \right|^2}$ and ${\left| {E_ - ^r({\boldsymbol{r}}_ \bot ^r)} \right|^2}$ (the field intensity of the LCP and RCP components of the reflected beam) with the angle of incidence θ_i. The intensity distribution patterns of these two components undergo significant changes as varying the θ_i and have opposite intensity evolutions, forming a two-lobe intensity distribution at EP. It is noteworthy that the phase distributions of the LCP and RCP component have opposite signs at the EP [inset of figure 4(a)], indicating that their intensity distributions have opposite variation characteristics. When the linearly polarized beam is incident on both sides of the EP, the intensity distribution has a noticeable centroid shift in the transverse y-direction, exhibiting a giant and opposite spin-Hall shift (figure 4(b)), i.e. Δy₋ = −Δy₊, In particular, this displacement vanishes at EPs, indicating the complete suppression of the SHE. Besides, there are also in-plane shifts, which reach their maximum value at the EP [inset of figure 5(b)]. Although this value is relatively small compared to the displacement in the y-direction, it is important to note that the SHE is generally a weak phenomenon [7, 8].

Zoom In Zoom Out Reset image size

We then consider that a p-polarized beam is incident from the backward direction into the system. ${\left| {E_ + ^r({\boldsymbol{r}}_ \bot ^r)} \right|^2}$ and ${\left| {E_ - ^r({\boldsymbol{r}}_ \bot ^r)} \right|^2}$ vary with the incident angle θ_i, as depicted in figure 5(a). Both components also show a two-lobe intensity pattern, but with a phase difference of π/2 from forward incidence [insets in figures 4(a) and 5(a)]. Figure 5(b) demonstrates the shift of the reflected beam near the EPs. Analogous to the scenario in figure 4(b), the reflected LCP and RCP components have opposite shifts, yet vanish at the EP. Analogous to the scenario in figure 4(b), the reflected LCP and RCP components have opposite shifts but disappear at the EP, accompanied by small in-plane shifts that are minimised at the EP [figure 6(b) inset]. It is remarkably that the transverse shift is much smaller when the light is incident from the backward direction than when it is incident from the forward direction.

Zoom In Zoom Out Reset image size

Next, we examine the scenario where the p-polarized light beam is incident from the forward direction, but results in a two-lobe intensity distribution oriented at an angle of 45 degree. As shown in figure 7(a), the intensity patterns of the reflected LCP and RCP components show great changes with respect to the incidence angle θ_i around the EP. The reflected beam intensity forms pronounced oblique two-lobe patterns that differ from those shown in figures 5 and 6. The transverse shift is significantly smaller compared to the two cases, while the associated in-plane shift is significantly larger (figure 7(b)).

Zoom In Zoom Out Reset image size