Cluster dynamics modeling of hydrogen retention and desorption in tungsten with saturation and multi-trapping effect of sinks

The CD model assumes that defects diffuse within a homogeneous medium, where they can absorb and emit other defects, leading to their evolution over large time and length scales. To facilitate the modeling process, several reasonable assumptions are made, including:

(1) The basic types of defects included in the model are self-interstitial atoms (SIAs, I), vacancies (V), hydrogen atoms (H) and their complex clusters formed by binary reactions (${I_{\text{n}}},{V_{\text{n}}},HI,{H_{\text{m}}}{V_{\text{n}}}$, where m and n represent the number of point defects in a loop/cluster). In addition, other inherent sinks are also included like dislocation lines (DLs) and grain boundaries (GBs).

(2) On the one hand, only a few interstitial clusters can be formed under the implantation of 2 keV D ions. On the other hand, DFT calculations have found that H trapping energies in small $H{I_{\text{n}}}$ complexes are approximately 0.3 eV in W [29, 30]. This suggests that ${I_{\text{n}}}$ clusters are not effective trapping sites for H, as most trapped H can be released from $H{I_{\text{n}}}$ below room temperature [25]. For the sake of simplification, it is thus reasonable to neglect the impact of interstitial clusters on H retention and desorption here.

(3) In theory, the mobility of different defects is determined by their respective migration energies and the sample temperature. However, the concentration of large defect clusters formed is relatively low under H implantation at low incident energies (below several keV). Thus, the influence on defect evolution can be neglected even without considering the mobility of these large clusters. To simplify our model, we assume that only SIAs (I), di-interstitials (${I_2}$), vacancies (V) and hydrogen atoms (H) are mobile, while all other defect clusters are considered immobile.

The evolution of these defects is described by a set of master equations, which can be expressed as,

$$\begin{align}\frac{{\partial {C_{\unicode{x03B8}} }}}{{\partial t}} & = {G_{\unicode{x03B8}} } + {D_{\unicode{x03B8}}}{\nabla ^2}{C_{\unicode{x03B8}} } + \mathop {\mathop \sum \nolimits }\limits_{{\unicode{x03B8}} ^{\prime} } \left[ {\omega \left( {\theta ^{\prime} ,\theta } \right){C_{{\unicode{x03B8}}^{\prime} }} - \omega \left( {\theta ,\theta {^{^{\prime}}}} \right){C_{\unicode{x03B8}} }} \right] - {L_{\unicode{x03B8}} },\end{align} \tag{ 1 }$$

where ${C_{\unicode{x03B8}} }\left( {\theta = I,{I_2},V,H,{I_\text{n}},{V_\text{n}},HI,{H_\text{m}}{V_\text{n}}} \right)$ (in the unit of m⁻³) is the concentration of defect $\theta$. On the right-hand side of equation (1), the first term ${G_{\unicode{x03B8}} }$ (in the unit of m⁻³ · s⁻¹) represents the generation rate of defects. For H implantation, our open-source program IM3D is used to simulate the primary radiation damage for defect generation [31]. The second term accounts for the spatial diffusion of defects, where ${D_{\unicode{x03B8}} }$ (in the unit of ${{\text{m}}^2}\cdot{{\text{s}}^{ - 1}}$) denotes the defect diffusion coefficients. The third term describes the sum of all the forward and reverse reactions, where $\omega \left( {\theta ^{\prime},\theta } \right)$ (in the unit of s⁻¹) represents the transition rate coefficient per unit concentration of a defect of type $\theta ^{\prime}$ to a defect of type $\theta$ (as listed in table 1). Due to low vacancy concentrations, and small rate coefficients $k_{\text{V} + {\text{V}_\text{n}}}^ +$ resulting from the large diffusion barrier for monovacancies in W, the forward reaction flux between V and V_n exhibits a relatively low magnitude under low-energy D irradiation here. This aligns with first-principles studies which demonstrates that the interaction of bi-vacancies is predominantly repulsive in W because of the negative values of the binding energies between monovacancies [32, 33]. Therefore, for the sake of computational efficiency, these reactions can be simplified or disregarded.

Table 1. Reaction types and the corresponding rate coefficients.

$\begin{array}{*{20}{l}} {I + V\mathop \rightleftharpoons \limits_{{G_\text{I/V}}}^{k_\text{I+V}^ + } 0} \\ {I + {I_\text{n}}\mathop \rightleftharpoons \limits_{k_{{\text{I}_\text{n+1}}}^ - }^{k_{\text{I} + {\text{I}_\text{n}}}^ + } {I_\text{n+1}}} \\ {I + {V_\text{n}}\mathop \to \limits^{k_{\text{I} + {\text{V}_\text{n}}}^ + } {V_\text{n-1}}(n \unicode{x2A7E} 2)} \\ {I + H\mathop \rightleftharpoons \limits_{k_\text{HI}^ - }^{k_\text{I+H}^ + } HI} \end{array}$

$\begin{array}{*{20}{l}} {I + {H_\text{m}}V\mathop \to \limits^{k_{\text{I}+{\text{H}_\text{m}}\text{V}}^+} mH} \\ {I + {H_\text{m}}{V_\text{n}}\mathop \to \limits^{k_{\text{I}+{\text{H}_\text{m}}{\text{V}_\text{n}}}^+}{H_\text{m}}{V_\text{n-1}}(n \unicode{x2A7E} 2)} \\ {I + mGB\mathop \to \limits^{k_{\text{mgb,I}}^ + } mGI} \\ {I + DL\mathop \to \limits^{k_\text{d,I}^ + } DI} \\ {{I_2} + {I_\text{n}}\mathop \rightleftharpoons \limits_{k_{{\text{I}_\text{n+2}}}^ - }^{k_{{\text{I}_2} + {\text{I}_\text{n}}}^ + } {I_\text{n+2}}} \end{array}$

$\begin{array}{*{20}{l}} {{I_2} + V\mathop \to \limits^{k_{{\text{I}_2} + \text{V}}^ + } I} \\ {{I_2} + {V_\text{n}}\mathop \to \limits^{k_{{\text{I}_2} + {\text{V}_\text{n}}}^ + } {V_\text{n-2}}(n \unicode{x2A7E} 2)} \\ {{I_2} + {H_\text{m}}{V_2}\mathop \to \limits^{k_{{\text{I}_2} + {\text{H}_\text{m}}{\text{V}_2}}^ + } mH} \\ {{I_2} + {H_\text{m}}{V_\text{n}}\mathop \to \limits^{k_{{\text{I}_2} + {\text{H}_\text{m}}{\text{V}_\text{n}}}^ + } {H_\text{m}}{V_\text{n-2}}(n \unicode{x2A7E} 3)} \\ {V + {I_\text{n}}\mathop \rightleftharpoons \limits_{k_{{\text{I}_\text{n-1}} - \text{V}}^ - }^{k_{\text{V} + {\text{I}_\text{n}}}^ + } {I_\text{n-1}}} \end{array}$

$\begin{array}{*{20}{l}} {V + {V_\text{n}}\mathop \rightleftharpoons \limits_{k_{{\text{V}_\text{n+1}}}^ - }^{k_{\text{V} + {\text{V}_\text{n}}}^ + } {\text{V}_\text{n+1}}} \\ {V + HI\mathop \to \limits^{k_\text{V+HI}^ + } H} \\ {V + {H_\text{m}}{V_\text{n}}\mathop \rightleftharpoons \limits_{k_{{\text{H}_\text{m}}{\text{V}_\text{n+1}}}^ - }^{k_{\text{V} + {\text{H}_\text{m}}{\text{V}_\text{n}}}^ + } {H_\text{m}}{V_\text{n+1}}} \\ {V + mGB\mathop \to \limits^{k_\text{mgb,V}^ + } mGV} \end{array}$

$\begin{array}{*{20}{l}} {V + DL\mathop \to \limits^{k_\text{d,V}^ + } DV} \\ {H + {V_\text{n}}\mathop \rightleftharpoons \limits_{k_{\text{H}{\text{V}_\text{n}}}^ - }^{k_{\text{H} + {\text{V}_\text{n}}}^ + } H{V_\text{n}}} \\ {H + {H_\text{m}}{V_\text{n}}\mathop \rightleftharpoons \limits_{k_{{H_\text{m+1}}{\text{V}_\text{n}}}^ - }^{k_{\text{H} + {\text{H}_\text{m}}{\text{V}_\text{n}}}^ + } {H_\text{m+1}}{V_\text{n}}} \end{array}$

$\begin{array}{*{20}{l}} {H + mGB\mathop \rightleftharpoons \limits_{k_{{\text{mgb,H}}}^ - }^{k_{{\text{mgb,H}}}^ + } mGH} \\ {H + DL\mathop \rightleftharpoons \limits_{k_{{\text{d,H}}}^ - }^{k_{{\text{d,H}}}^ + } DH} \end{array}$

The final term refers to the absorption of point defects (I/V/H) by inherent sinks including DLs and GBs here. In most previous CD models like IRadMat, it is simply expressed as,

$$\begin{align}{L_{\unicode{x03B8}} } & = {D_{\unicode{x03B8}} }{C_{\unicode{x03B8}} }\left( {k_{{\text{d}},{\unicode{x03B8}} }^ + + k_{{\text{gb}},{\unicode{x03B8}} }^ + } \right),\end{align} \tag{ 2 }$$

where $k_{{\text{d,}}\theta }^{\text{ + }}$ and $k_{{\text{gb,}}\theta }^ +$ are the sink strengths (in the unit of m⁻²) of DLs and GBs to defect $\theta$, respectively. They can be estimated by the dislocation density ${\rho _{\text{d}}}$ and the grain size d [34, 35] that,

$$\begin{align}k_{{\text{d,}}{\unicode{x03B8}} }^ + & = {\rho _{\text{d}}}Z_{\text{d}}^{\unicode{x03B8}} ,\end{align} \tag{ 3 }$$

and

$$\begin{align}k_{{\text{gb,}}{\unicode{x03B8}} }^ + & = k_{{\text{sc}}}^{\unicode{x03B8}} \left[ {\frac{{d\sqrt {k_{{\text{sc}}}^{\unicode{x03B8}} } }}{2}\coth \left( {\frac{{d\sqrt {k_{{\text{sc}}}^{\unicode{x03B8}} } }}{2}} \right) - 1} \right]\nonumber \\ & \quad {\left[ {1 + \frac{{k_{{\text{sc}}}^{\unicode{x03B8}} {d^2}}}{{12}} - \frac{{d\sqrt {k_{{\text{sc}}}^{\unicode{x03B8}} } }}{2}\coth \left( {\frac{{d\sqrt {k_{{\text{sc}}}^{\unicode{x03B8}} } }}{2}} \right)} \right]^{ - 1}},\end{align} \tag{ 4 }$$

respectively, where $Z_{\text{d}}^{\unicode{x03B8}}$ is the dimensionless capture efficiency, and $k_{{\text{sc}}}^{\unicode{x03B8}}$ represents the total sink strength from all other microstructures in a single crystal except for GBs.

However, a polycrystalline sample is composed of multiple independent grains that are separated by GBs with various interface areas. The interactions between GBs and H atoms are also characterized by different binding energies. Therefore, it becomes necessary to consider multiple trapping effects caused by various types of GBs in IRadMat-TDS. For m-type GB, its interface area ${S_\text{m}}$ can be defined as,

$$\begin{align}{S_\text{m}} & = {S_{{\text{total}}}} \cdot {x_\text{m}}.\end{align} \tag{ 5 }$$

Here, ${S_{{\text{total}}}}$ represents the total interface area of all GBs in the material, while ${x_\text{m}}$ denotes the area proportion of m-type GB ($\mathop \sum \limits_{m = 1}^{{N_{{\text{gb}}}}} {x_\text{m}} = 1$, where ${N_{{\text{gb}}}}$ is the number of GB types). Since the interface area per volume (in the unit of m⁻¹) can be derived from $6/d$, by substituting equation (5) into equation (4), the sink strength of m-type GB becomes that,

$$\begin{align}k_{{\text{mgb,}}{\unicode{x03B8}} }^ + & = k_{{\text{sc}}}^{\unicode{x03B8}} \left[ {\frac{{d\sqrt {k_{{\text{sc}}}^{\unicode{x03B8}} } }}{{2{x_\text{m}}}}\coth \left( {\frac{{d\sqrt {k_{{\text{sc}}}^{\unicode{x03B8}} } }}{{2{x_\text{m}}}}} \right) - 1} \right] \nonumber \\ & \quad {\left[ {1 + \frac{{k_{{\text{sc}}}^{\unicode{x03B8}} {d^2}}}{{12x_\text{m}^{\text{2}}}} - \frac{{d\sqrt {k_{{\text{sc}}}^{\unicode{x03B8}} } }}{{2{x_\text{m}}}}\coth \left( {\frac{{d\sqrt {k_{{\text{sc}}}^{\unicode{x03B8}} } }}{{2{x_\text{m}}}}} \right)} \right]^{ - 1}}.\end{align} \tag{ 6 }$$

In most previous CD models like IRadMat, the absorption of H in GBs and DLs is approximatively seen as infinite absorption. However, Zhou et al have shown that the ∑5(310) tilt GB in W can accommodate no more than two H atoms by DFT calculations [36]. This finding suggests that the absorption by GBs reaches saturation with the increasing number of trapped H atoms. Therefore, it is necessary to set saturated concentrations of trapped H in inherent defects in IRadMat-TDS that,

$$\begin{align}{C_{{\text{d,H}}}} & \unicode{x2A7D} C_{{\text{d,H}}}^{\max }\sim {n_{\text{d}}} \cdot {\rho _{\text{d}}}\end{align} \tag{ 7 }$$

and

$$\begin{align}{C_{{\text{mgb,H}}}} & \unicode{x2A7D} C_{{\text{mgb,H}}}^{\max }\sim {n_{{\text{gb}}}} \cdot 6{x_\text{m}}/d.\end{align} \tag{ 8 }$$

Here, ${C_{{\text{d,H}}}}$ and ${C_{{\text{gb,H}}}}$ (in the unit of m⁻³) are the volume concentrations of H in DLs and m-type GB, respectively. $C_{{\text{d,H}}}^{\max }$ and $C_{{\text{mgb,H}}}^{\max }$ (in the unit of m⁻³) are the saturated volume concentrations of H in DLs and m-type GB, respectively. ${n_{\text{d}}}$ (in the unit of ${{\text{m}}^{ - 1}}$) and ${n_{{\text{gb}}}}$ (in the unit of m⁻²) are the number of trapping sites per unit length in DLs and per unit area in GBs, respectively.

Generally, intrinsic point defects (I/V) are considered not to be emitted from inherent defects in most previous models [37]. However, the emission of H from DLs/GBs cannot be neglected especially during heating process. The ratios of absorption rate coefficients to emission rate coefficients of H in DLs and GBs from [37] can be transformed to,

$$\begin{align}\frac{{k_{{\text{d,H}}}^ - {D_{\text{H}}}}}{{k_{{\text{d,H}}}^ + {D_{\text{H}}}}} & = \frac{b}{{{\rho _{\text{d}}}{V_{{\text{at}}}}}}\exp \left( {\frac{{ - E_{{\text{d,H}}}^{\text{b}}}}{{{k_{\text{B}}}T}}} \right),\end{align} \tag{ 9 }$$

and

$$\begin{align}\frac{{k_{{\text{mgb,H}}}^ - {D_{\text{H}}}}}{{k_{{\text{mgb,H}}}^ + {D_{\text{H}}}}} & = \frac{{{b^2}d}}{{6{x_\text{m}}{V_{{\text{at}}}}}}\exp \left( {\frac{{ - E_{{\text{mgb,H}}}^{\text{b}}}}{{{k_{\text{B}}}T}}} \right),\end{align} \tag{ 10 }$$

respectively. $k_{{\text{dl,H}}}^ - {D_{\text{H}}}$ and $k_{{\text{mgb,H}}}^ - {D_{\text{H}}}$ represent the emission rate coefficients of H from DLs and m-type GB, respectively. b denotes the Burgers vector. $E_{{\text{d,H}}}^{\text{b}}$ and $E_{{\text{mgb,H}}}^{\text{b}}$ are the binding energies between H and DLs or m-type GB, respectively. Here, the additional factors of $1/{\rho _{\text{d}}}$ and $d/6{x_\text{m}}$ arise from the transformations from H linear concentrations in DLs ($C_{_{{\text{d,H}}}}^{\text{l}}$, in the unit of m⁻¹) and H surface concentrations in m-type GB ($C_{_{{\text{mgb,H}}}}^{\text{s}}$, in the unit of m⁻²) to H volume concentrations, ${C_{{\text{d,H}}}}$ and ${C_{{\text{mgb,H}}}}$, respectively. These conversions are based on the relationships $C_{_{{\text{d,H}}}}^{\text{l}} = {C_{{\text{d,H}}}}/{\rho _{\text{d}}}$ and $C_{_{{\text{mgb,H}}}}^{\text{s}} = {C_{{\text{mgb,H}}}}/\left( {6{x_\text{m}}/d} \right)$.

From equations (6) and (10), it can be seen that the absorption and desorption of H in multiple GBs can be characterized by two key parameters: the area proportion of m-type GB, ${x_\text{m}}$, and its binding energy with H, $E_{{\text{mgb,H}}}^{\text{b}}$. According to first-principles calculations, H atoms have a tendency to occupy the trapping sites in GBs with randomly available free volumes that are typically smaller compared to vacancies. Moreover, as more H atoms are introduced into GBs, the available volumes for H decreases, with the weak absorption of multiple H atoms by a single GB. Thus, the binding energies of H with various GBs generally fall in the range of 0–1.2 eV. These energies vary randomly due to different types of GBs and numbers of trapped H, up to the binding energy between H and vacancies [38] and approaching zero with the increasing number of trapped H [39–41]. Experimental findings indicate that the average binding energy associated with the H desorption peak from GBs in TDS is approximately 0.6 eV [13, 15], which coincides with the theoretical average value. Therefore, it is reasonable to assume that the distribution of various types of GBs and their respective binding energies with H follow a Gaussian distribution. The peak of this distribution represents the most probable binding energy of GBs. Consequently, we can assume that the Gaussian probability of binding energies, $E_{{\text{mgb,H}}}^{\text{b}}$, corresponds to the area proportion of m-type GB, ${x_\text{m}}$. With these assumptions and according to equation (6), the sink strengths of various GBs should also exhibit a similar Gaussian distribution.

Finally, the improved absorption term of H by DLs and GBs can be written by,

$$\begin{align}L_{\text{H}}^{{\text{dl}}} & = {D_{\text{H}}}Z_{\text{d}}^{\text{H}}\left[ {{\rho _{\text{d}}}{C_{\text{H}}} - \frac{b}{{{V_{{\text{at}}}}}}\exp \left( {\frac{{ - E_{{\text{d,H}}}^{\text{b}}}}{{{k_{\text{B}}}T}}} \right){C_{{\text{d,H}}}}} \right],\;{C_{{\text{d,H}}}} \unicode{x2A7D} C_{{\text{d,H}}}^{\max },\end{align} \tag{ 11 }$$

and

$$\begin{align}L_{\text{H}}^{{\text{gb}}} & = \mathop \sum \limits_{m = 1}^{{\text{N}_\text{gb}}} k_{{\text{mgb,H}}}^ + {D_{\text{H}}}\left[ \!{{C_{\text{H}}} - \frac{{{b^2}d}}{{6{x_\text{m}}{V_{{\text{at}}}}}}\exp \left(\! {\frac{{ - E_{{\text{mgb,H}}}^{\text{b}}}}{{{k_{\text{B}}}T}}} \!\right){C_{{\text{mgb,H}}}}} \!\right],\,\nonumber \\{C_{{\text{mgb,H}}}} & \unicode{x2A7D} C_{{\text{mgb,H}}}^{\max },\end{align} \tag{ 12 }$$

respectively.

During TDS measurement, H isotopes retained in the sample can desorb from various defects/sinks with distinct de-trapping energies, leading to the variation of the gas release rate. In general, this method is relatively simple and effective in determining both the total H retention and characteristic temperatures of H release from the material.

Our CD simulation involves four main steps, namely implantation, isothermal annealing, continuous linear temperature annealing and TDS analysis. By solving the ordinary differential equations, we can obtain the total retained amount ${R_{\text{T}}}$ (in the unit of m⁻²) at different temperatures. Therefore, the total desorption amount ${W_{\text{T}}}$ (in the unit of m⁻²) can be determined by subtracting the total retained amount ${R_{\text{T}}}$ from the initial retained amount ${R_{\text{0}}}$ that,

$$\begin{align}{W_{\text{T}}} & = {R_0} - {R_{\text{T}}}.\end{align} \tag{ 13 }$$

Thus, the desorption rate of D (in the unit of m⁻² · s⁻¹) as a function of temperature, namely TDS spectrum, can be given using the following equation,

$$\begin{align}\frac{{{\text{d}}W}}{{{\text{d}}t}} & = \frac{{{\text{d}}W}}{{{\text{d}}T}} \times \frac{{{\text{d}}T}}{{{\text{d}}t}}.\end{align} \tag{ 14 }$$

Besides quantitative simulation of the total TDS, the contributions of various defects to the total retention/desorption can be accurately determined from the concentration evolution ${C_{\unicode{x03B8}} }(n,t,z,T)$ in terms of size, depth, time and temperature, as shown in figure 1(c). During the simulation of thermal annealing, it is noteworthy that as H diffuses from the bulk to the surface, it may become trapped in various defects and subsequently released. The concentrations of trapped and released H in these defects change dynamically and can re-engage in reactions between different defects. Therefore, our model inherently accounts for the re-trapping process of H.

In order to achieve a more comprehensive understanding of the experimental results, we calibrate our CD simulation using data from Taylor et al's experiments [42]. We selected these TDS experiments based on their clear detection of low-temperature desorption peaks typically from about 300–700 K. These low-temperature desorption peaks always appear in almost all measured TDS for H in W, but their attributions have yet to be clearly identified [12–15]. To ensure the reliability and accuracy of our model, we carefully choose the fundamental kinetic and energetic parameters by considering the published values from ab initio/MD calculations or experiments, as shown in table 2. Further details of the transition rate coefficients can be found elsewhere [26–28]. The capillary law [43] is used to extrapolate the binding energies of mobile point defects with different types of large clusters. The binding energies between H and H_m V_n are obtained from ab initio calculations for small sizes and extrapolated for large sizes as described in [44]. Figure 2 presents the initial depth distributions of the displacements (I/V) and D implantation calculated by IM3D. D ions with 2 keV energy can cause damage and implantation at depths of tens of nanometers in W.

Zoom In Zoom Out Reset image size

Table 2. Summary of simulation parameters.

Parameter	Symbol	Value	Reference
Sample thickness	—	50 μm	[42]
Irradiation temperature	—	317 K	[42]
Implantation fluxes	—	1.2 × 1019–2.8 × 1019 D m−2 · s	[42]
Implantation fluences	—	3.2 × 1020–3.2 × 1022 D · m−2	[42]
Lattice constant	${a_0}$	0.3165 Å	[45]
Grain size	d	10 μm	[46]
Dislocation density	${\rho _{\text{d}}}$	1012 m−2	[47]
Recombination radius	${r_\text{IV}}$	4.65 Å	[27]
Interstitial pre-exponential factor	${D_{{\text{I}_0}}}$	10−8 m−2 · s−1	[47]
Vacancy pre-exponential factor	${D_{{\text{V}_{\text{0}}}}}$	1.77 × 10−6 m−2 · s−1	[48]
D pre-exponential factor	${D_{{\text{H}_{\text{0}}}}}$	4.1 × 10−7 m−2 · s−1	[49]
SIA/dislocation elastic interaction	$Z_\text{D}^{\text{I}}$	1.2	[50]
Formation energy of SIA	$E_\text{I}^{\text{f}}$	9.466 eV	[51]
Formation energy of V	$E_\text{V}^{\text{f}}$	3.80 eV	[51]
Formation energy of H	$E_\text{H}^{\text{f}}$	2.45 eV	[34]
Migration energy of SIA	$E_\text{I}^{\text{m}}$	0.013 eV	[52]
Migration energy of V	$E_\text{V}^{\text{m}}$	1.66 eV	[52]
Migration energy of H	$E_\text{H}^{\text{m}}$	0.39 eV	[53]
Binding energy of I2	$E_{{\text{I}_{\text{2}}}}^{\text{b}}$	2.12 eV	[54]
Binding energy of V2	$E_{{\text{V}_{\text{2}}}}^{\text{b}}$	−0.115 eV	[54]
Binding energy of H-I	$E_{{\text{HI}}}^{\text{b}}$	0.33 eV	[55]
Binding energy of H-DL	$E_{{\text{dl,H}}}^{\text{b}}$	0.53 eV	[56]
Binding energy of H-GB	$E_{{\text{gb,H}}}^{\text{b}}$	0.64 eV	[40]

By utilizing the parameters listed above, we can simulate the total amount of retained D after 2 keV D ion irradiation with the fluences ranging from 3.2 × 10²⁰ to 3.2 × 10²² D · m⁻² (corresponding to fluxes between 1.2 × 10¹⁹ and 2.8 × 10¹⁹ D · m⁻² · s^–1). The simulated data is compared with all of the literature data shown in figure 3(a). According to Taylor's experiments, the total retention exhibits a slow increase with increasing fluence, varying by only one order of magnitude [42]. This modest growth is similar to the finding in Sakamoto's experiments [57] in the intermedia fluence region of 10²⁰–10²² D · m⁻². However, the simulated retention, which does not consider the saturated absorption and emission by inherent sinks, shows a rapid linear increase, spanning nearly two orders of magnitude. This discrepancy indicates that the assumption of infinite absorption by GBs and DLs in previous models could be unreasonable at high fluences. In fact, as the fluence increases, the free trapping sites in GBs and DLs could gradually fill up. As mentioned in section 2.1, theoretical studies have also shown that the absorption of H in GBs and DLs may reach saturation with the increasing number of trapped H. After incorporating the saturated absorption and emission of H in GBs and DLs, the simulated retention (red dotted line in figure 3(a)) thus shows good agreement with the experimental results at different fluences. The observed increase in total retention is consistent with the higher D concentration at elevated fluences.

Zoom In Zoom Out Reset image size

Figure 3(b) shows the comparison between our simulated TDS and experimental results after 2 keV D ion irradiation with a fluence of 10²² D · m⁻². The simulation successfully reproduces both the positions and intensities of the two distinct desorption peaks at around 490 and 550 K, respectively. Obviously, the low-temperature peak exhibits a higher intensity, indicating a significant contribution from low-temperature traps. Nevertheless, the simulated TDS displays a narrower width compared to the experimental spectrum, corresponding to the lower simulated total retention in figure 3(a). The narrower width of the spectrum should be attributed to the absence of describing certain complex physical processes, such as the desorption of D from the multi-trapping effect of sinks (like GBs and DLs) and specific defects (like D-induced voids). Further discussion about this discrepancy can be found in section 3.3.

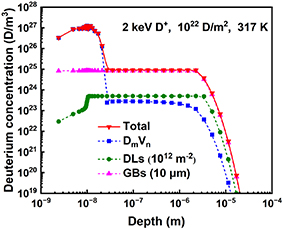
In the following, we will focus on the comprehensive mechanisms of D retention and desorption in W. Figure 4 shows the depth distributions of the total retained D, ${D_\text{m}}{V_\text{n}}$ clusters, and the absorption of D by DLs and GBs, respectively. Three typical regions of H depth distribution are revealed as expected [5]: (1) the near-surface heavily damaged zone (up to tens of nanometers as the same as ion implantation depth), which exhibits a remarkable ${D_\text{m}}{V_\text{n}}$ concentration peak. (2) The sub-surface platform region (from tens of nanometers to several microns) due to the saturated absorption of D by GBs and DLs. (3) The declining region in the bulk owing to the attenuation of D concentration by diffusion.

Zoom In Zoom Out Reset image size

Figure 5(a) presents the simulated total and partial D retention as a function of the annealing temperature. The amount of D trapped in DLs is relatively low and begins to diminish at approximately 350 K. In contrast, the amount of D trapped in GBs is remarkable and exhibits a decline after about 450 K. Additionally, the retention of D in the form of ${D_\text{m}}{V_\text{n}}$ undergoes an obvious drop around 550 K. In fact, these variations indicate different rates of H desorption from different defects/sinks with distinct de-trapping energies. Following the method given in section 2.2, the total and partial TDS spectra are simulated accordingly, as shown in figure 5(b). According to the simulated partial TDS, the peak at around 490 K mainly arises from the release of D from GBs. The shoulder at approximately 550 K can be attributed to D desorption from irradiation-induced vacancies. Most of the conclusions drawn from previous TDS measurements of D in W have emphasized the contribution of single vacancies while ignoring the roles of GBs and DLs [6, 58, 59]. Some studies also simply attributed the low-temperature desorption peaks to the trapping of D in low-temperature defects without identifying the specific defect types [7, 10]. However, our research explicitly reveals that D retention in GBs is more pronounced than that in DLs.

Zoom In Zoom Out Reset image size

The integral area of the GBs and vacancy peaks contributes approximately 70% and 30% to the total release, respectively. In contrast, the desorption of D from DLs is negligible. In fact, we can estimate these ratios in principle as follows: firstly, GBs and DLs are uniformly distributed throughout the whole W bulk. The number of trapping sites per unit area in GBs, ${n_{{\text{gb}}}}$, is theoretically proportional to the inverse square of the distance (d₀) between two nearby trapping sites, $1/d_{\text{0}}^{\text{2}}$. Since this distance d₀ is typically on the order of angstroms (10⁻¹⁰ m), the value of ${n_{{\text{gb}}}}$ should thus be on the order of 10²⁰ m⁻². Similarly, the number of trapping sites per unit length in DLs, ${n_{\text{d}}}$, is proportional to $1/{d_0}$ and thus on the order of 10¹⁰ m⁻¹. Therefore, the theoretical limit of D concentration retained in GBs (with grain size of 10⁻⁵ m) is about 10²⁵ m⁻³, which is at least 3 orders of magnitude higher than that in DLs (with dislocation density of 10¹² m⁻²) of about 10²² m⁻³. Secondly, despite a high concentration of lattice displacements near the surface, approximately 10²⁹ m⁻³ as shown in figure 2, the concentration of vacancies diminishes significantly beyond 20 nm depth. As a result, the eventual amount of D retained in vacancies falls somewhere between those in GBs and DLs. It thus provides an easy way to identify the attribution of the characterized peaks in TDS, by just considering the densities of vacancies, GBs and DLs.

Overall, the mechanisms of low-energy D retention and desorption in polycrystalline W can be summarized as: (1) the total D retention is mostly contributed by D trapped in GBs. (2) D retention in DLs is negligible. (3) D trapped in vacancies near the surface accounts for an intermediate portion of total D retention. By splitting the partial TDS, defect types and their respective contributions to TDS are explicitly identified. This clarifies the previously ambiguous attribution of desorption peaks. Moreover, it makes us effectively address the long-standing dispute over quantitative characteristics of H retention in typical defects within H-W systems.

The simulated TDS reproduces the experimental peak positions and intensity well, but not the peak width. We have analyzed three factors that could cause the narrowing of the main peak and the shoulder. Firstly, the narrow peak width at 490 K could potentially be attributed to the use of single binding energy $E_{{\text{gb,H}}}^{\text{b}}$(=0.64 eV) that fails to truthfully describe the multiple interactions between D and various types of GBs in polycrystalline W. Secondly, the extended shoulder in the experimental TDS, ranging from 570 to 700 K, could be due to H desorption from high-temperature traps, particularly large D-induced sinks like vacancy clusters and dislocation loops. Numerous studies have shown that low-energy, high-flux D plasma irradiation on W can cause the formation of cavities/blisters due to the increase of dislocation or void density induced by D supersaturation near the surface [60–67]. The formation of large blisters observed in the experimental samples further supports this hypothesis [42]. Thirdly, measurement errors in both the heating furnace and thermocouple could potentially cause deviations in the peak width between experimental and simulated results more or less.

Here, we consider the complex interactions between D and various types of GBs as an example for improving the simulated peak width. As mentioned in section 2.1, an accurate characterization of the multi-trapping effect of GBs necessitates a comprehensive assessment of the absorption and emission of D in different GBs, as determined by the area proportion of m-type GB (${x_\text{m}}$) and its binding energy with D ($E_{{\text{mgb,H}}}^{\text{b}}$). Given the limited detailed information on specific GB energy distributions from both experimental and theoretical sources, we select six energy values that follow a fitted Gaussian distribution. This distribution has a mean of approximately 0.63 eV and a full width at half maximum of about 0.14 eV. The area proportions of GBs with these six energies correspond to respective Gaussian probabilities. Table 3 summarizes the six values of $E_{{\text{mgb,H}}}^{\text{b}}$ and ${x_\text{m}}$ used in our simulation. Figure 6(a) presents the intensity differences of the corresponding individual GB peaks after simulation. It is evident that as the binding energies increase from 0.41 to 0.80 eV, the corresponding peak intensity initially increases and then decreases, reaching a maximum at 0.64 eV. The resulting convolution of these individual peaks ultimately contributes to the broad GBs desorption peak. In addition, the partial desorption fluxes for GBs marked 3–6 appear to be negative in figure 6(a). It indicates that the previously released D from GBs with lower binding energies are subsequently re-trapped in GBs with higher binding energies. We will discuss this indirect desorption behavior of D in more detail in the future.

Zoom In Zoom Out Reset image size

Table 3. Binding energies and interface area proportion of different types of GBs.

m	$E_{{\text{mgb,H}}}^{\text{b}}$ (eV)	${x_\text{m}}$
1	0.41	0.0125
2	0.52	0.1170
3	0.60	0.3413
4	0.64	0.4302
5	0.72	0.0873
6	0.80	0.0101

Figure 6(b) shows a comparison between the total TDS simulated with and without the multi-trapping effect of GBs. The total TDS simulated with the multi-trapping effect (blue line) exhibits a noticeable broadening on the left side compared to that without the multi-trapping effect (red line). It suggests that the single-site approximation for GBs is primarily responsible for the previously simulated narrow peak near 490 K. As mentioned above, the narrow shoulder on the right side of the simulated TDS should be attributed to the neglect of the capture of D by D-induced sinks. In recent years, some researchers have attempted to explain hydrogen bubble formation and severe blistering phenomena by proposing mechanisms such as 'loop punching' and 'vacancy clustering' [60–67]. Even so, the underlying mechanism of the formation of D-induced sinks is still far from clear. In addition, accurately modeling the detailed size and depth distribution of D-induced sinks is always a significant challenge. Therefore, it is really hard to improve the width of the simulated shoulder. Nevertheless, the interaction between D and these induced sinks is similar to the interaction between D and GBs. The improvement in the peak width due to GBs provides compelling evidence that the previously narrow shoulder in the simulated TDS is caused by the same mechanism.