Abstract
The geo-effectiveness of coronal mass ejections (CMEs) is a critical area of study in space weather, particularly in the lesser-explored domain of CME–CME interactions and their geomagnetic consequences. This study leverages the Space Weather Adaptive SimulaTion framework to perform 3D MHD simulation of a range of CME–CME interaction scenarios within realistic solar wind conditions. The focus is on the dynamics of the initial magnetic flux, speed, density, and tilt of CMEs, and their individual and combined impacts on the disturbance storm time (Dst) index. Additionally, the kinematic, magnetic, and structural impacts on the leading CME, as well as the mixing of both CMEs, are analyzed. Time-series in situ studies are conducted through virtual spacecraft positioned along three different longitudes at 1 au. Our findings reveal that CME–CME interactions are nonuniform along different longitudes, due to the inhomogeneous ambient solar wind conditions. A significant increase in the momentum and kinetic energy of the leading CME is observed due to collisions with the trailing CME, along with the formation of reverse shocks in cases of strong interaction. These reverse shocks lead to complex wave patterns inside CME2, which can prolong the storm recovery phase. Furthermore, we observe that the minimum Dst value decreases with an increase in the initial density, tilt, and speed of the trailing CME.

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Coronal mass ejections (CMEs) are significant drivers of space weather, characterized by the ejection of massive amounts of magnetized plasma from the Sun's corona. When multiple CMEs are launched in quick succession, their interactions—termed CME–CME interactions—can dramatically enhance their space weather impact. CME–CME interactions occur when a faster CME overtakes a slower one, leading to a complex interplay of their shocks, magnetic fields, and plasma structures. Studying these interactions is crucial, as they can significantly amplify geomagnetic storms, particle acceleration, and other space weather phenomena, posing greater risks to technological systems and human activities (N. Gopalswamy et al. 2001; N. Lugaz et al. 2017; C. Scolini et al. 2020).
The complexity of CME–CME interactions arises from the already intricate dynamics present in individual CME and solar wind (SW) interactions. In single CME–SW interactions, ambient SW conditions can significantly modify the CME's trajectory, speed, internal properties, and structure (M. Temmer et al. 2011; F. Shen et al. 2012b; C. Wu et al. 2016; P. Mayank et al. 2023). When a trailing CME catches up and collides with a leading CME, resulting in a CME–CME–SW interaction, the scenario becomes even more complex. Studies have reported a wide range of collision types between CMEs, from inelastic (W. Mishra et al. 2014), nearly elastic (W. Mishra et al. 2015), and superelastic collisions (C. Shen et al. 2012a) to merging-like processes (M. Temmer et al. 2012).
Multiple observational and simulation studies have made significant progress in understanding the evolution of CMEs during interactions. F. Shen et al. (2016) showed that the final speeds depend on the relative masses of the CMEs as well as their relative speeds. Through 2.5D simulations, S. Poedts et al. (2003) noted that the acceleration of the leading CME increases as the mass of the trailing CME increases. In addition to speed, CME–CME interactions can also lead to the deflection of the CMEs (N. Lugaz et al. 2012; C. Shen et al. 2012a). Observational and simulation-based studies have also demonstrated that the expansion of the radial width of the leading CME decreases as the trailing CME impacts and compresses its rear (N. Lugaz et al. 2005; M. Xiong et al. 2006).
In addition to changes in CME properties, multiple studies have elucidated the behavior of shocks within magnetic clouds. M. Vandas et al. (1997) highlighted that shocks propagate more swiftly inside magnetic clouds due to enhanced fast magnetosonic speeds, potentially leading to shock–shock merging near the cloud's nose, while maintaining distinct shocks at the flanks. Other numerical studies have also reported that weak or slow shocks within regions of elevated magnetosonic speeds dissipate inside the magnetic cloud (M. Xiong et al. 2006; N. Lugaz et al. 2007). Additionally, C. J. Farrugia & D. B. Berdichevsky (2004) have reported the merging or dissipation of shocks through Helios and ISEE-3 measurements, showing a decrease from four shocks at 0.67 au to two at 1 au. N. Lugaz et al. (2005) provided a comprehensive analysis, delineating four primary phases of shock property changes during such interactions.
Several studies have observed that CME–CME interactions are a common source of double-dip and multiple-dip geomagnetic storms (I. G. Richardson & J. Zhang 2008; J. Zhang et al. 2008). Much of the understanding of the impact of a CME's initial properties—that is, right after eruption, measured at around 0.1 au—on their geo-effectiveness has come from MHD simulations. C. Scolini et al. (2020) quantified the impact of interactions on the geo-effectiveness of individual CMEs using the European heliospheric forecasting information asset (J. Pomoell & S. Poedts 2018) spheromak CME model. They found that the time intervals between the CME eruptions and their relative speeds are critical factors in determining the resulting impact of the CME–CME structure. Additionally, G. J. Koehn et al. (2022) conducted MHD simulations of spheromak CMEs with a uniform outflowing SW and found that the orientation and handedness of a given CME can significantly impact the conservation and loss of magnetic flux in the CME.
Although several observational studies have shown the consequences of CME–CME interactions, they have not been very successful in elucidating the interaction process itself. Most studies have primarily focused on different aspects of the interaction, without attempting to explore a global view. While multiple numerical studies have provided great insights into these interaction processes, particularly shock evolution, there have been very few studies on CME–CME interactions occurring within realistic dynamic ambient SW conditions (C. Scolini et al. 2020). Given the complexities and limitations in observational and simplified simulation studies, MHD ensemble simulations with realistic SW backgrounds offer a powerful tool for obtaining a global view.
In this work, we use the Space Weather Adaptive Simulation framework (SWASTi; P. Mayank et al. 2022, 2023) to conduct ensemble MHD simulations with a data-driven SW background. Our aim is to identify global trends and understand the impact of initial CME properties on the geo-effectiveness of the CME–CME structure. We used the SWASTi-CME module to simulate two successive flux-rope CMEs and trace their evolution in the inner heliosphere. Further, we quantified their geo-effectiveness using the empirical disturbance storm time (Dst) relation given by T. O'Brien & R. L. McPherron (2000).
The rest of the paper is organized as follows. Section 2 provides a brief description of the numerical models for the SW, CMEs, and Dst index used in this work. In Section 3, we describe the ensemble cases, with initial values of CMEs and an overview of the CME–CME–SW interaction scenario. Section 4 contains the ensemble simulation results and a detailed analysis of the evolution of the shock and leading CME properties. Further, Section 5 presents a statistical analysis of the variations in the minimum and cumulative Dst indices. Finally, Section 6 provides the discussion and conclusions of the work.
2. Numerical Models
To perform the ensemble study of CME–CME interactions within a realistic SW background, we utilized the SWASTi framework. The three-dimensional physics-based models for the SW and CMEs are described in the following subsections. Additionally, an empirical Dst relation, based on in situ plasma properties, has been employed to analyze the geo-effectiveness of these energetic events. The relevant equations and comparisons with some specific events are presented in subsequent subsections.
2.1. SW Model
In order to simulate the background SW, we used observation-based inputs from the GONG magnetogram, which provides the magnetic field at the solar surface. The field lines are then extrapolated to source surface using the potential-field source-surface (M. D. Altschuler & G. Newkirk 1969) technique. Based on this extrapolation, the SW speed at the initial boundary of the MHD domain (Vin), located at 0.1 au, is determined using a modified version of the Wang–Sheeley–Arge (WSA) relation (C. N. Arge 2003):
where v1, v2, and β are parameters set at 250 km s−1, 675 km s−1, and 1.25, respectively. fs represents the areal expansion factor of the flux tube, d is the minimum angular separation of the footpoint from the coronal hole boundary, and w is the median of d for field lines that extend to Earth's location. The initial density at 0.1 au was estimated by equating the kinetic energy (KE) due to the obtained WSA speed with that of the fast SW. Here, we have assumed fast-wind parameters, as nfsw = 200 cm−3 and speed vfsw = 600 km s−1. The temperature was determined based on a constant thermal pressure of 6.0 nPa. The magnetic field was derived from a velocity-dependent empirical relation. For the detailed methodology, readers can refer to Section 2 of P. Mayank et al. (2022). In this study, the magnetic field strength (Bfsw) associated with 650 km s−1 is assumed to be 300 nT at the MHD domain's initial boundary.
After setting the necessary parameters at 0.1 au, based on the semi-empirical coronal model, the time-dependent 3D ideal MHD equations were solved using the PLUTO code (A. Mignone et al. 2007). Computations were conducted on a uniform static grid in spherical coordinates, employing a finite volume method for the simulation. The set of conservative equations used in the MHD simulations is outlined in P. Mayank et al. (2022), with a specific heat ratio of 1.5 for the SW plasma. The computational domain for the heliosphere extended from 0.1 au to 2.1 au radially (r), ±60° azimuthally (θ), and 0° to 360° meridionally (ϕ), structured on a grid resolution of 512 × 61 × 181.
2.2. CME Model
To simulate magnetized CMEs, we employed the CME module of the SWASTi framework (P. Mayank et al. 2023), which is based on the Flux Rope in 3D (FRi3D; A. Isavnin 2016) model. This model incorporates the three-dimensional magnetic field configuration of a CME and accounts for major deformations, to accurately reconstruct its global geometrical shape. In this study, the FRi3D model was used to construct the 3D magnetized shell of the CME at 0.1 au, serving as the initial state for the MHD domain. The CME geometry forms a classic croissant-like shape, anchored at both ends to the Sun in the beginning and then cut for the nonhindrance eruption of the trailing CME.
For single-flux-rope CMEs, cutting the legs when their speed matches the ambient SW is commonly used to ensure smooth integration with the background. However, in CME–CME interactions, this timing becomes more complex, as the trailing CME may erupt before the leading CME legs have slowed enough for cutting. Additionally, this method does not ensure a consistent CME structure across different cases with varying inner-boundary conditions, which is critical for this study. To address these issues, we implemented a fixed-duration insertion process for all simulation cases, where the duration was optimized to ensure that the average CME leg speed closely matches the ambient SW. This approach maintains structural consistency across all simulations and minimizes disruptions in the SW outflow from the inner boundary.
Initially, the cross section of the CME is assumed to be circular, with the radius varying in proportion to the heliocentric distance. The CME structure is populated with magnetic field lines that have a constant twist of 2. In this work, the center of the CME footpoints was set at 0° latitude and 0° longitude. All CMEs had the following fixed parameters: flattening = 0.5, pancaking =0.6, chirality = −1, polarity = −1, half-width = 45°, and half-height = 22 5. Other properties were varied in the ensemble study, with their exact values detailed in Section 3.
5. Other properties were varied in the ensemble study, with their exact values detailed in Section 3.
Once the FRi3D CME structure is formed with its leading edge at 0.1 au, it is allowed to evolve in the MHD domain. The process of integrating the CME into the MHD domain involves gradually updating the boundary conditions to match the evolving CME structure, ensuring a smooth transition and accurate representation of the CME's impact on the surrounding SW. Overall, the use of a flux-rope CME model in this study provides a detailed and realistic simulation of CME–CME interactions, allowing for a comprehensive analysis of their evolution and the influence of initial conditions on geo-effectiveness.
2.3. Dst Estimation
We use the Dst index to quantify the geo-effectiveness of the simulated CME plasma cloud. The Dst index estimates the storm-time ring current strength without the influence of the magnetopause and quiet-time ring currents (T. O'Brien & R. L. McPherron 2000). There are many other indices that may be used to describe the coupling between the SW and the magnetosphere (see M. Lockwood 2022 for a good summary), but since we are most interested in the kinds of intense events that would arise from the effect of merged CMEs on the geomagnetic field, we feel that Dst is an appropriate proxy for this study.
To quantify the geo-effectiveness of the CME–CME structure upon its arrival at 1 au, we positioned virtual spacecraft within the simulation domain at 0° (along the Sun–Earth line) and ±10° longitudes. These virtual spacecraft recorded the plasma properties in real time with a 5 minutes cadence. Based on these in situ properties, the Dst indices at each time step were computed using the empirical equations provided by T. O'Brien & R. L. McPherron (2000). Further details about the equations used and their comparison with observed events are presented in Appendix A.
3. Simulation Cases
To investigate the evolution and geo-effectiveness of CME–CME interaction events, we conducted a series of simulations involving two interacting CMEs, with second CME having varying attributes. The primary objective was to understand how alterations in the initial coronal properties—such as speed, density, and magnetic flux—affect their interaction, in situ properties, and the Dst index at 1 au. This focus is driven by the understanding that the in situ speed, density, and southward magnetic field component play a pivotal role in determining the intensity of geomagnetic storms. Therefore, assessing the effects of these initial conditions at 1 au is crucial. Moreover, recent research highlighting the significance of CME tilt in heliospheric evolution (N. Lugaz et al. 2013; P. Mayank et al. 2023) prompted us to also examine the impact of relative tilt between interacting CMEs.
For this ensemble simulation, we selected the background SW conditions from the Carrington rotation (CR) 2270 period, corresponding to 2023 April. This period was particularly significant, due to an intense geomagnetic storm caused by a halo CME eruption. The Dst values of this CME are discussed in Appendix A, where the empirical Dst is compared with the observed values. In the simulation, the first CME (hereafter referred as CME1) was injected at the inner boundary (0.1 au) on 2023 May 12 at 3:00, with the second CME (hereafter referred as CME2) following 25 hr later. This schedule was optimized to ensure that CME2 reaches 0.1 au after the complete insertion of CME1 in the computational domain and they have significant interaction before reaching 1 au.
Several studies have highlighted the influence of ambient SW on CME evolution (M. Temmer et al. 2011; C. Wu et al. 2016; P. Mayank et al. 2023). To ascertain if similar impacts are present in CME–CME interactions, this study analyzes in situ profiles at three different longitudinal positions: 0° and ±10°. Here, 0° corresponds to the Sun–Earth line, while −10° and +10° represent the eastern and western sides of the solar disk, respectively. Additionally, the projected trajectory allows CME1 to interact with a stream interaction region (SIR), thereby enabling a detailed study of the potential impact of inhomogeneity in ambient SW.
To determine the optimal number of cases for the ensemble study, our objective was to select a sufficient number of cases to identify trends in the properties while ensuring each case could be thoroughly analyzed. To examine the effects of speed, density, and magnetic flux, we varied these parameters for CME2 while keeping CME1's values constant. Specifically, for CME2, we employed two sets of density and magnetic flux values, one set lower and another higher than CME1's values. Furthermore, we chose two velocity values for CME2, both higher than the first's and increasing incrementally, to guarantee their interaction before 1 au. Regarding the relative tilt, two tilt angles were applied to CME2, while the tilt of CME1 was kept constant. The overarching approach was to maintain consistent properties for CME1 across all cases, thereby enabling a direct comparison with a single CME1 simulation.
The specific values of the properties for the various cases are presented in Table 1. With two values for each of the four properties, the total number of cases in this ensemble study amounts to 16. The density of the CMEs was set of the order of 10−18 kg m−3 (M. Temmer et al. 2021), while the magnetic flux values were between 1012 and 1013 Wb (C. Scolini et al. 2020). The CME apex speed values ranged approximately from 1300 to 1500 km s−1, and the tilt values were 0° and 45°. To facilitate clear and easy reference during discussion, each case has been assigned a specific nomenclature. This naming convention consists of four elements: the first two letters denote low-speed (LS)/high-speed (HS) CMEs, followed by a pair of letters for low-density (LD)/high-density (HD) and magnetic flux, respectively. The final character in each case name denotes the tilt, with "0" representing no tilt and "1" indicating a 45° tilt. For example, the name "HSHDLF1" corresponds to a case with higher speed, higher density, lower magnetic flux, and a 45° tilt of CME2 with respect to the first. Additionally, a simulation of just CME1 was conducted to serve as a basis for comparing all interaction cases, thereby highlighting the impact of such interactions on the front CME.
Table 1. CME Initial Properties of All the Ensemble Cases
| Case No. | Name | Vel_t | Density | Magnetic Flux | Tilt |
|---|---|---|---|---|---|
| (103 km s−1) | (10−18 kg m−3) | (1012 Wb) | (deg) | ||
| Case 0 | Single CME | vt 1 = 0.8 | ρ1 = 3 | ΦB 1 = 7 | τ1 = 0 |
| Case 1 | LSLDLF0 | vt 2 = 1 | ρ2 = 1 | ΦB 2 = 5 | τ2 = 0 |
| Case 2 | LSLDLF1 | vt 2 = 1 | ρ2 = 1 | ΦB 2 = 5 | τ2 = 45 |
| Case 3 | LSLDHF0 | vt 2 = 1 | ρ2 = 1 | ΦB 2 = 9 | τ2 = 0 |
| Case 4 | LSLDHF1 | vt 2 = 1 | ρ2 = 1 | ΦB 2 = 9 | τ2 = 45 |
| Case 5 | LSHDLF0 | vt 2 = 1 | ρ2 = 5 | ΦB 2 = 5 | τ2 = 0 |
| Case 6 | LSHDLF1 | vt 2 = 1 | ρ2 = 5 | ΦB 2 = 5 | τ2 = 45 |
| Case 7 | LSHDHF0 | vt 2 = 1 | ρ2 = 5 | ΦB 2 = 9 | τ2 = 0 |
| Case 8 | LSHDHF1 | vt 2 = 1 | ρ2 = 5 | ΦB 2 = 9 | τ2 = 45 |
| Case 9 | HSLDLF0 | vt 2 = 1.1 | ρ2 = 1 | ΦB 2 = 5 | τ2 = 0 |
| Case 10 | HSLDLF1 | vt 2 = 1.1 | ρ2 = 1 | ΦB 2 = 5 | τ2 = 45 |
| Case 11 | HSLDHF0 | vt 2 = 1.1 | ρ2 = 1 | ΦB 2 = 9 | τ2 = 0 |
| Case 12 | HSLDHF1 | vt 2 = 1.1 | ρ2 = 1 | ΦB 2 = 9 | τ2 = 45 |
| Case 13 | HSHDLF0 | vt 2 = 1.1 | ρ2 = 5 | ΦB 2 = 5 | τ2 = 0 |
| Case 14 | HSHDLF1 | vt 2 = 1.1 | ρ2 = 5 | ΦB 2 = 5 | τ2 = 45 |
| Case 15 | HSHDHF0 | vt 2 = 1.1 | ρ2 = 5 | ΦB 2 = 9 | τ2 = 0 |
| Case 16 | HSHDHF1 | vt 2 = 1.1 | ρ2 = 5 | ΦB 2 = 9 | τ2=45 |
Download table as: ASCIITypeset image
Figure 1(a) presents a snapshot capturing the evolution of two interacting CMEs in the inner heliosphere, corresponding to the LSLDLF0 case as CME1 reaches 1 au. It reveals a 2D cross section of the speed profile along the r − ϕ plane at 0° latitude, alongside 3D isosurfaces of the two CMEs. The background SW speed is depicted using a color map, with CME1 outlined in crimson and CME2 in a white hue. This image also illustrates the asymmetric expansion of CME1's leading edge, shaped by the variable speeds of the ambient SW streams.
Figure 1. Subplot (a) displays a 3D view of the leading (crimson) and trailing (white) structures of the CMEs, overlaid on a 2D snapshot of the SW speed in the equatorial plane. The dashed white box indicates the regions shown in subplots (b) and (c). They depict the traced CME boundaries for cases (b) LSLDLF0 and (c) LSHDLF0, with color-filled contours illustrating the plasma speed regions: slow, fast, and >600 km s−1. The gray line contours indicate HD regions, with darker shades representing higher scaled densities. The blue, green, and orange dots mark the positions of virtual spacecraft at −10°, 0°, and +10°.
Download figure:
Standard image High-resolution imageFigure 1(b) provides a detailed cutout from Figure 1(a), while Figure 1(c) is akin to Figure 1(b) but represents the LSHDLF0 case. The red- and teal-colored contours represent the traced boundaries in the equatorial plane of the 3D CME structures shown in Figure 1(a). These subplots showcase filled contours for speed as well as line contours for scaled density. The three dots at 1 au mark the positions of virtual spacecraft measuring in situ plasma properties at 0° and ± 10° longitudes. Notably, there is a fast stream at ϕ = −10° and a slow-speed stream at ϕ = +10°, with the ϕ = 0° location approximately at the juncture of these streams. Due to this, the disparity in the expansion of CME1's flanks is apparent along these longitudes, with the top flank showing a more pronounced expansion compared to the bottom flank. The SIR has a higher density, as compared to fast or slow streams, making them more effective in compressing CME1 when CME2 approaches from behind, as depicted in Figure 1(c). Here, the intensified compression along −10° longitude is clearly visible.
It is important to emphasize that the dark orange regions of HS do not necessarily represent shock structures but rather highlight areas where the speed exceeds 600 km s−1. Comparing Figures 1(b) and (c), the >600 km s−1 region in Figure 1(c) extends significantly farther in both the radial and longitudinal directions. Specifically, this HS region extends about 0.3 au radially and covers approximately 30° in Figure 1(b), while in Figure 1(c) it stretches to around 0.5 au radially and spans roughly 75°, indicating a stronger shock associated with CME2 in the HD case. Additionally, the increased radial width across all longitudes in Figure 1(c) suggests that CME2 has expanded more, leading to greater compression of CME1. A more detailed analysis of the evolution of the CMEs in the heliosphere is discussed in the subsequent section.
4. Evolution in Heliosphere
One of the key aspects of CME–CME interaction is the change in their properties as they traverse the inner heliosphere. The nature and extent of this interaction play a critical role in determining their characteristics upon reaching Earth. These alterations directly affect space weather forecasting, underscoring the importance of understanding these dynamic processes. Through ensemble 3D MHD simulations with realistic SW conditions, we have sought to explore the following dynamics.
4.1. Shock Dynamics
The complex process of CME–CME interaction can be segmented into progressive phases based on the trailing shock associated with CME2. N. Lugaz et al. (2005) identified four distinct stages:
- 1.The shock propagates through the SW before reaching the rear of CME1;
- 2.Upon impact, the shock advances inside CME1;
- 3.Subsequently, the shock begins interacting with the sheath of CME1;
- 4.Finally, the merging of the shocks commences.
All interaction scenarios evolve through these stages, and depending on the properties of the CMEs, the specific stage at which they arrive at 1 au may vary.
Figure 2 demonstrates these evolutionary stages. The subplots display the temperature profile in a logarithmic scale, emphasizing the sharp gradient of the shock associated with CME2. The corresponding scaled density profile is shown in Figure 12. In both figures, subplots (a1)–(a4) pertain to the LSLDLF0 case, while subplots (b1)–(b4) relate to the LSHDLF0 case, each separated by a time interval of 6.65 hr. The only difference between the upper and lower rows is the density of CME2. Although initially similar, as time progresses, significant differences emerge. The interaction commences earlier in the HD case, with the trailing shock penetrating deeper into the leading magnetic cloud than in the LD case. As CME1 reaches 1 au, the HD case nearly reaches stage 4, while the LD case has just entered stage 3. Notably, when different longitudes are considered, both cases exhibit varying stages at each location. Thus, depending on the portion of the CME–CME interaction structure encountering Earth, it may be at a different stage of evolution.
Figure 2. The subplots demonstrate the evolution of the trailing shock in the inner heliosphere for cases LSLDLF0 (a1–a4) and LSHDLF0 (b1–b4). The displayed color map corresponds to the plasma temperature on the logarithmic scale.
Download figure:
Standard image High-resolution image4.1.1. Nonuniform Shock Interaction
Most of the previous studies (N. Lugaz et al. 2017 and references therein) have focused on defining a single stage for the entire CME–CME interaction structure. However, given the relatively small scale of Earth's magnetosphere compared to the CME structure, examining the evolution of these stages at different longitudes is critical. For instance, the structures passing through the 1 au locations marked by the three dots in Figure 2 at 0° and ±10° longitudes are at different stages. The trailing shock does not extend to the sheath of CME1 along the −10° longitude in any of the cases. The radial evolution of this shock is greater along 0° and even more so along +10°, where it interacts with the sheath and merges with the first shock in some instances. The uneven evolution of these stages is primarily caused by the deformation of CME1 due to the ambient SW preceding it, particularly due to the SIR in front of it in these specific situations. This SIR positions the top flank of the CME predominantly within the fast-SW stream, while the bottom flank experiences a significantly stronger antiradial drag force. This dynamic results in an overexpansion of the upper flank and an underexpansion of the lower flank, as depicted in Figure 1.
This four-stage evolution concept can be applied both globally across the entire structure and locally along different longitudes to study the progression of CME–CME interactions comprehensively. To facilitate a robust comparison of different cases with varying initial properties, it is crucial to identify both global and local stages. For this purpose, we utilize the concept of virtual spacecraft to observe the in situ plasma conditions at the front and rear of CME1 along three longitudes (0° and ±10°). Six comoving virtual spacecraft were positioned, with three at the rear and three at the front of CME1. Figure 3 displays the in situ speed profiles collected by these spacecraft for the HSHDLF0 case. In Figure 3(a), the solid lines represent data from the rear of CME1, while the dashed lines are from the front. At the rear of CME1, the trailing shock arrives with a time difference of 1 hr between the ±10° longitudes, resulting in a similar speed jump along these longitudes due to the equivalent shock propagation time. However, at the front of CME1, the arrival time difference of the trailing shock between these longitudes is much larger. This is because the radial width of CME1 varies significantly between +10° and −10° longitudes, leading to an enhanced temporal gap in shock arrival. Furthermore, since the radial extent of CME1 is greater along −10°, the trailing shock travels a longer distance and loses more energy, resulting in a smaller speed jump compared to +10° longitude.
Figure 3. The arrival of the trailing shock at the rear and at the front of CME1. Subplot (a) shows the result for the HSHDLF0 case along 0° and ±10°. Subplot (b) depicts the speed variation at the rear of CME1, along −10°, for all cases with 0° tilt. Similarly, subplot (c) shows the speed at the front of CME1.
Download figure:
Standard image High-resolution image4.1.2. Shock Propagation Duration
For comparison across all ensemble cases, we focused on +10° longitude to study the properties of shock propagation. This approach examines the time it takes for the trailing shock to travel from the rear to the front of CME1, a duration primarily influenced by two factors: the radial width of CME1 and the strength of the trailing shock. Given that the CME1 properties remain consistent across all cases, the strength of the trailing shock emerges as the sole determinant of this duration. The bottom left and right subplots of Figure 3 illustrate the arrival and departure times of the trailing shock from the CME1 structure, revealing two distinct behaviors influenced by the initial density of CME2. The speed jump due to the shock is consistently higher in all HD cases compared to all LD cases. Although the HD cases have similar arrival times, the sharpness of the shock is greatest in the HSHDHF case and least in the LSHDLF case. As the trailing shock reaches the front of CME1, the temporal differences between the cases become more pronounced, with the shock propagation duration for the strongest-shock (HSHDHF0) and weakest-shock (LSLDLF1) cases widening from 13.3 to 28.26 hr.
The trailing shock propagation time (Δ) for all ensemble cases is presented in Table 2. The duration is shortest for the HSHDHF case, in both the with and without relative tilt scenarios, and it progressively increases as the initial flux, speed, and density decrease, with the longest duration observed in the LSLDLF case. Cases with a higher initial density consistently exhibit shorter Δ values. Since this duration is directly correlated with the shock strength, it suggests that higher-density CMEs generate stronger shocks. Elevated density leads to an increase in internal pressure within the CME, which amplifies the pressure differential with the ambient SW. This, in turn, results in an accelerated rate of CME expansion. Moreover, greater momentum allows the CME to plow more effectively through the SW plasma, especially in the LD environment of the preconditioned SW. Therefore, a combination of a faster expansion rate and more efficient plowing contributes to the observed trend. Furthermore, cases with 0° tilt consistently show smaller Δ values compared to those with 45° tilt. This could potentially be due to the preconditioned SW: CME2, having no relative tilt, follows the same trajectory as CME1 and encounters less drag force from the LD SW swept by CME1. However, with nonzero relative tilt, the structure of CME2 does not completely align with the cleared path and faces greater resistance from the ambient SW, potentially leading to a reduction in shock strength.
Table 2. Trailing Shock Propagation Time Inside CME1 for all Ensemble Cases
| Case | Δ | Case | Δ |
|---|---|---|---|
| (hr) | (hr) | ||
| HSHDHF0 | 13.30 | HSHDHF1 | 16.62 |
| HSHDLF0 | 14.96 | HSHDLF1 | 16.62 |
| LSHDHF0 | 14.96 | LSHDHF1 | 18.28 |
| LSHDLF0 | 16.62 | LSHDLF1 | 19.95 |
| HSLDHF0 | 23.27 | HSLDHF1 | 24.93 |
| HSLDLF0 | 23.27 | HSLDLF1 | 24.93 |
| LSLDHF0 | 23.27 | LSLDHF1 | 24.93 |
| LSLDLF0 | 26.60 | LSLDLF1 | 28.26 |
Download table as: ASCIITypeset image
4.1.3. Reverse Shock Formation
As the trailing shock progresses inside the first magnetic cloud, the rear CME begins colliding with the first. This collision starts in stage 2, where the trailing shock accelerates the rear of CME1. Depending on the advancement of the shock, the difference in speed between the rear of CME1 and the front of CME2 can exceed or fall below the local fast magnetosonic speed. When this speed is exceeded, the trailing CME pushes the plasma faster than the leading CME can smoothly adjust, leading to the formation of a shock wave directed toward CME2.
Fast reverse shocks associated with SIRs and their corresponding in situ properties have been well studied (E. Kilpua et al. 2015; D. M. Oliveira 2016). However, their formation due to CME–CME interaction has not been reported until very recently, by D. Trotta et al. (2024) using Solar Orbiter observations. Similar in situ features have also been observed through virtual spacecraft in our simulation. The bottom row of Figure 4 (subplots (a2), (b2), and (c2)) demonstrates the existence of fast reverse shocks. The characteristic feature of anticorrelation between plasma speed and magnetic field and density can also be seen. As this reverse fast-mode shock wave propagates antiradially, it compresses the downstream plasma inside CME2, resulting in higher plasma density in the downstream region compared to the upstream region. Conversely, the effective plasma speed will be lower in the downstream region due to the antiradial direction of the shock, leading to an anticorrelation between speed and density profiles.
Figure 4. This figure showcases the propagation of reverse shocks inside CME2. The top subplots ((a1), (b1), and (c1)) show in situ measurements from virtual spacecraft as CME2 of the HSHDHF0 case passes through, highlighting forward shocks (FSs) and reverse shocks (RSs). The bottom subplots display 2D snapshots of (a2) radial velocity (km s−1), (b2) density (log scale, N cm–3), and (c2) magnetic field strength (log scale, nT). The white contour indicates the boundary of CME2.
Download figure:
Standard image High-resolution imageGiven the nonuniform interaction demonstrated in earlier sections, the deformation of CME1 causes the collision to initiate in one or more localized areas rather than across the entire interface simultaneously. This nonuniformity leads to the generation of independent shock fronts in each of these areas. The interactions among these shocks can lead to complex dynamics, including the merging of shocks, the amplification or attenuation of wave fronts, and the formation of complex wave patterns. Figure 4 illustrates this complexity, showing the reverse shock's propagation in the rear magnetic cloud for the HSHDHF0 case. Inside CME2, a complex pattern of alternating compressed and rarefied zones is visible, manifesting as ripple-like structures in the in situ plots. Such variations hold the potential to influence the duration of geomagnetic storms.
4.2. Impact on First CME
One of the crucial aspects of CME–CME interaction is the alteration in the properties of CMEs, particularly the first CME. This ensemble study, in which the first CME (CME1) remains constant while the second CME (CME2) varies across different cases, offers a unique approach to analyzing how CME1 is influenced by various CME2 scenarios. Drawing from previous studies (F. Shen et al. 2017 and references therein), our analysis primarily focuses on changes in the total momentum, KE, magnetic energy (ME), and radial extent of CME1 resulting from its interaction with CME2. The overarching approach is to examine the temporal evolution of the impacts on CME1 caused by different CME2 scenarios. To facilitate this, we compare the simulations of a single first CME, case 0, with those from the ensemble cases, cases 1–16. The premise is that any observed changes in CME1 in cases 1–16, relative to the CME in case 0, are due to the influence of CME2.
4.2.1. Kinematics
The subplots (a1), (a2), (d1), and (d2) of Figure 5 illustrate the percentage change in the total radial momentum (TRM) of CME1, which is calculated using following equations:
Figure 5. The subplots demonstrate the temporal evolution of change in the radial momentum, total KE, and total ME of CME1 for cases 1–16, with respect to the single-CME case.
Download figure:
Standard image High-resolution imageHere, the subscript "i" represents cases 1–16, while "0" denotes case 0. ρj , , and dVj are the mass density, radial velocity, and volume of the grid cell "j," respectively. The TRM is the summation of the radial momentum at each grid cell. Based on the slope of the momentum profile, we interpret the temporal evolution of momentum change in CME1 in two distinct phases: the Rising Phase and the Diminishing Phase.
The Rising Phase commences when the trailing shock from CME2 impacts the rear of CME1. During this phase, the effective total momentum of CME1 starts to increase, due to the local velocity increase of the CME1 plasma. As the shock propagates deeper into CME1, the total momentum continues to rise. This momentum increase of CME1 solely due to the trailing shock occurs very briefly (1–2 hr), followed by the collision of the trailing sheath and magnetic cloud with CME1. This collision initiates a substantial momentum exchange between the two CMEs. The high-velocity trailing CME2 exerts significant force on the slower-moving CME1, resulting in a notable increase in CME1's total momentum. During this phase, the rate of momentum increase (indicated by the slope of the momentum curve) achieves its highest value, reflecting the extent of the direct and robust transfer of momentum from CME2 to CME1.
In the final Diminishing Phase, CME2 has transferred a considerable amount of its momentum to CME1, significantly reducing its own momentum. This momentum exchange decreases the relative speed between the two CMEs. Despite the reduction, CME2 still maintains a higher speed than CME1 and continues to push it forward, albeit with diminishing force. Consequently, the rate of change in momentum for CME1 gradually decreases, indicating that the interaction force is waning and the system is approaching a new equilibrium state.
The transition between phases is quite smooth, making it challenging to define rigid boundaries. Relatively speaking, the Rising Phase has an average duration of approximately 10 hr, after which the Diminishing Phase persists. The exact duration of this transition varies across different cases. For the HSHDHF case, the Diminishing Phase starts earliest, at roughly 7 hr, whereas for the LSLDLF case, it takes the longest time, approximately 13 hr. For cases with relative tilt between CMEs, this transition period is slightly shorter compared to cases with no relative tilt.
The momentum gained by CME1, from the start of the interaction to the phase transition point and until the combined structure reaches 1 au, also varies significantly with the initial conditions of CME2. The eight cases shown in the subplots can be clustered into two groups: HD and LD cases. After 10 hr of interaction between CME1 and CME2, CME1 in HD cases gains approximately 5%–15% more momentum, whereas in LD cases, it gains 1%–5% more momentum. This momentum gain is slightly higher for cases with no relative tilt compared to cases with relative tilt. Moreover, the difference between the HD and LD cases is also more pronounced for the no-relative-tilt cases.
As the CME–CME structure reaches 1 au, starting from 25 hr, the difference in momentum gain between the HD and LD cases becomes more pronounced. Since shock strength is inversely correlated with shock propagation time, which is shorter for HD cases (see Table 2), these cases exhibit higher momentum gain. Additionally, CME2 in HD cases has more initial momentum to impart than in LD cases. After 30 hr of interaction, CME1 in HD cases demonstrates a 20%–40% increase in momentum compared to 7%–12% in LD scenarios. The gap between these two clusters of cases becomes 16% in the absence of relative tilt compared to 8% in the presence of tilt.
Since the total KE (KE = ) of a radially evolving CME1 is related to its TRM, a similarity between the two is expected. The subplots (b1), (b2), (e1), and (e2) of Figure 5 depict the temporal evolution of the percentage change in the KE of CME1 for cases 1–16 relative to case 0. These subplots closely resemble the momentum plots but indicate a greater gain. On average, the percentage gain in KE is about two-thirds greater than the percentage gain in momentum of CME1 due to the interaction process. As with momentum, the eight cases can be clustered into two groups, based on their initial density. The difference between these two groups is more pronounced in the absence of relative tilt (up to 25%) compared to scenarios with nonzero tilt (up to 18%). After 30 hr of interaction, CME1 gains up to 60% more KE in the HSHDHF case and up to 20% more in the LSLDLF case, due to the interaction with CME2.
4.2.2. ME
The evolution of the total ME of CME1 differs significantly from the changes observed in momentum and KE. The subplots (c1), (c2), (f1), and (f2) of Figure 5 showcase the temporal evolution of the percentage change in ME of CME1. These subplots reveal distinct behaviors based on the initial density of CME2. In LD cases, the interaction has little to no effect on the ME of CME1. In contrast, HD cases exhibit an initial increase in ME of approximately 1%–3%, followed by a subsequent decrease. This pattern is consistent in both the tilt and no-tilt scenarios, although the changes in ME occur more rapidly in the presence of relative tilt.
As the interaction begins, CME2 compresses CME1, potentially increasing the magnetic field strength and, consequently, the total ME if magnetic flux is conserved. Since CME1 and CME2 have the same chirality, this compression could also induce magnetic reconnection and other instabilities (e.g., tearing mode and plasmoid instabilities), dissipating magnetic fields and converting ME into kinetic and thermal energy. Despite significant compression even in the LSLDLF case, the gain in ME for LD scenarios is almost negligible, suggesting the dissipation of the magnetic field may happen even in weaker collisions.
In HD cases, there is a noticeable increase in ME, implying that the rate of magnetic field strength enhancement due to compression initially exceeds the rate of magnetic dissipation. However, after approximately 25 hr of interaction, the ME begins to decrease, indicating that the rate of compression diminishes while the rate of magnetic dissipation becomes dominant, leading to a reduction in the total ME of CME1.
Unlike momentum and KE profiles, ME profiles can be categorized into three groups: LD cases, HD high-flux (HDHF) cases, and HD low-flux (HDLF) cases. Given the insignificant changes in ME for LD cases, their slopes are excluded from subplots (c2) and (f2), to highlight the behavior of the remaining cases. Comparing the HSHDHF (red) and HSHDLF (orange) cases, the initial rise in ME is greater for the HSHDHF case, but the subsequent decrease is also more rapid. After 30 hr of interaction, the effective ME is lower for the HSHDHF case. This trend is consistent when comparing the LSHDHF to LSHDLF cases and across the tilt and no-tilt scenarios. This suggests that a higher initial magnetic flux results in a greater initial gain in ME due to compression, followed by a more substantial decrease in ME due to magnetic dissipation.
4.2.3. Radial Extent
In the earlier sections, we demonstrated and discussed the nonuniform radial expansion of CME1 due to interactions with the SW from the front and CME2 from the rear (see Figures 1 and 2). We also noted in the last section that the only possible way of increasing the ME is the compression of CME1 due to CME2. Although multiple studies (M. Xiong et al. 2006; N. Lugaz et al. 2013, 2017) have examined the compression of the leading CME in CME–CME interactions, a quantitative analysis of the temporal evolution of this compression has not been performed.
Using the passive scalar tracing technique, we traced the CME1 structure and computed its radial compression along different longitudes. This method tracks plasma using the advection equation, allowing the study of transport and mixing without altering magnetic or fluid dynamics, as demonstrated in P. Mayank et al. (2023). By placing virtual spacecraft at the front and rear of CME1, we can measure the radial difference between them, thus determining the radial extent of CME1 along each longitude. Figure 6 shows the temporal evolution of the percentage change in CME1's radial width across all CME–CME interaction cases (1–16) versus the single-CME case, with maximum compression seen in the HSHDHF case and minimum in the LSLDLF case across −10°, 0°, and +10°.
Similar to the momentum, KE, and ME profiles, the compression features of the HD and LD cases are distinguishable in the subplots of Figure 6. Compression is consistently higher for HD cases from the onset, though no noticeable gap between the LSHDLF and HSLDHF cases appears until about 10 hr for the 45° tilt cases. At +10° (Figure 6(a1)), HD cases with 45° tilt (HD1) reach an 80% reduction over 30 hr, while LD1 shows 60% reduction. Along −10° (Figure 6(a2)), HD1 shows a 40% reduction and LD1 a 20% reduction. The absence of an SIR along this longitude means there is no significant obstruction to CME1's expansion from the front, resulting in less compression from the rear than at +10°, with a nearly constant decrease for all cases. At 0° (Figure 6(a3)), the HD1 cases show a 65% reduction compared to 45% for LD1, revealing that the presence of the SIR ahead of CME1 has an intermediate impact on this region, more than −10° but less than +10°.
Figure 6. Temporal evolution of the percentage change in the radial width of CME1 compared to the single-CME case. Results are presented along three longitudes (0° and ±10°) for all cases.
Download figure:
Standard image High-resolution imageThe abovementioned statistics pertain to cases with a 45° tilt between the CMEs. In cases with a 0° tilt (see Figure 6, panels (b1)–(b3)), the interaction begins slightly earlier, leading to faster and greater compression. On average, the compression in cases without tilt is approximately 5% greater than in cases with tilt. This suggests that the alignment of CME2 with CME1 can influence the efficiency of the compressive interaction. Due to this tilt-induced difference, an enhancement in the gap between the HD and LD cases is evident in Figure 6. When comparing the overall effect of CME2's initial properties, the HSHDHF case consistently shows the greatest compression, followed by the HSHDLF and LSHDHF cases.
4.3. Mixing of CMEs
In addition to the merging of shocks and alterations in CME properties, interactions between magnetic clouds can also lead to their merging. Multiple observational studies have suggested (N. Gopalswamy et al. 2001; L. F. Burlaga et al. 2002) and demonstrated (N. Lugaz et al. 2009; Y. D. Liu et al. 2012; M. Temmer et al. 2012) the merging of magnetic clouds in the inner heliosphere during CME–CME interactions. However, the extent of plasma mixing between two interacting CMEs remains largely unknown. In particular, a quantified study of this mixing and its dependence on other CME properties has not been conducted yet. Understanding this mixing is crucial, as it may influence the geo-effectiveness of CMEs, impacting the intensity and duration of geomagnetic storms.
4.3.1. Quantifying the Mixing of CMEs
To estimate the extent of the plasma mixing between the leading and trailing CMEs, we utilize the CME tracer described in earlier sections to define the boundary of the CME structure. This approach is analogous to methods used in studying the mixing of astrophysical jets (e.g., see S. Walg et al. 2013). To quantify this mixing, we define a mixing factor (), which represents the absolute mass fractions within a specific grid cell. We set for the case of no mixing, where only CME1 material is present, and for the case where only CME2 material is present. We set in the case of maximum absolute mixing, meaning equal amounts of CME1 and CME2 constituents are present within the grid cell. In this scenario, the mass fraction of CME1 is equal to the mass fraction of CME2.
At a given time (t) and distance ( r ), a tracer is advected by the flow and obtains values within the range . Here, corresponds to the absence of that CME within the cell, while corresponds to a cell purely containing the plasma of that CME. In this work, we have taken = 0.1 and = 1.0 for all CMEs. Given that a tracer value directly corresponds to the quantity of that CME, the mass fraction of CME1 (δ1) within a grid cell can be expressed as follows:
Similarly, the mass fraction of CME2 (δ2) can also be calculated. Furthermore, assuming that the mass fraction within a cell linearly scales with the amount of mixing, the mixing factor of the plasma of CME1 and CME2 in terms of their tracer values in a grid cell can be written as:
4.3.2. Analyzing the Mixing of CMEs
Figure 7 presents a 2D histogram of the calculated mixing factor values throughout the entire simulation domain for all ensemble cases at the time when the merged structure reaches 1 au. These values are computed for each grid cell within the computational domain and binned into eight uniform clusters, ranging from 0 to 2. A mixing factor of indicates the highest level of mixing (50%), meaning both CME1 and CME2 contribute equal amounts of plasma to that specific cell. The cases with and without relative tilt between the leading and trailing CMEs are plotted separately. The color of each block represents the number of grid cells associated with a specific amount of mixing (Y-axis) for each corresponding case (X-axis). For instance, in case 15, 261 grid cells have values between 0.75 and 1 (see Figure 7(b)).
Figure 7. Amount of mixing between CME1 and CME2 upon the interacting structure's arrival at 1 au. Subplots (a) and (b) show the mixing factor () for cases with 45° and 0° relative tilt between the CMEs, along with the number of grid cells corresponding to each bin. Subplots (c) and (d) present the mean percentage of CME1-CME2 mixing along the three longitudes (0° and ±10°) in the equatorial plane.
Download figure:
Standard image High-resolution imageThe most notable feature in these subplots corresponds to the HD cases (5–8 and 13–16), which exhibit a significantly larger volume of mixing. As discussed earlier, these scenarios also demonstrate stronger CME shocks, higher momentum exchange, and greater radial compression. This trend is consistent in terms of the extent of mixing, where values are several times higher in HD cases as compared to LD cases. The HS cases (9–16) also consistently exhibit greater mixing compared to LS cases. Although the difference is not as big as in HD versus LD cases, the trend is evident across all bins of mixing factor.
Apart from these global trends, we also observe nonuniform mixing across the CME2 front. Similar to the nonuniform interaction between the back of CME1 and the front of CME2 discussed in earlier sections, the bottom flank exhibited a higher percentage of mixing (100 × [1 − ]) compared to the upper flank. Panels (c) and (d) of Figure 7 show the mean percentage of mixing along +10° (bottom flank), −10° (upper flank), and 0° longitudes for the 45° and 0° cases, respectively. In these plots, the +10° region consistently exhibits nonzero mixing, with the highest percentage in almost all the cases, suggesting that the bottom flank of CME2 experiences more intense interaction with CME1. In contrast, along −10°, only three cases with a 45° tilt and none with a 0° tilt show any mixing, while the 0° region exhibits mixing in a total of eight cases. This pattern supports the observed asymmetry in interaction strength, where the bottom flank experiences stronger compression, enhancing the mixing process. This again highlights the impact of the inhomogeneous ambient SW, which causes nonuniform interaction and mixing of the interacting CMEs.
5. Geo-effectiveness
In the previous section, we discussed the evolution of CME–CME interactions and their impact on the kinematic, magnetic, and structural properties of CME1. From a geo-effectiveness perspective, it is crucial to understand how this evolution translates into in situ properties at 1 au. Specifically, we aim to determine how the interactions between two CMEs ultimately transform into plasma properties that will interact with the Earth's magnetosphere. To investigate this in depth, we placed three virtual spacecraft in our simulation at 0° and ±10° longitudes, as depicted in Figures 1 and 2.
The simulated time-series data—including speed, density, and Bz profiles at a 5 minutes cadence—extracted from the virtual spacecraft positions are presented in Appendix A. The features observed in the evolution of CME1 and CME2 are reflected in their in situ properties, which in turn lead to variations in the Dst profile. The next subsections delve into these changes in Dst, focusing specifically on variations in the overall trend, the minimum Dst value, and the cumulative Dst.
5.1. Dst Variation
Figure 8(a) showcases the variations in Dst values across the 16 cases at three different longitudes: +10° (green), 0° (blue), and −10° (orange). The shaded regions depict the difference between the values at ±10° (green and orange) and 0° (blue). The Figure 8(b) subplots present the temporal overlap of the Dst profiles corresponding to the 16 CME–CME interaction cases, along with the single-CME case (Case 0). The plotted Dst values are computed based on the method described in Section 2.3. The analysis of these Dst profiles can be segmented into two distinct phases: the main phase and the recovery phase, which is divided by the global minimum in the Dst profile. The effects of the varying strengths of shocks, sheath regions, and CME1 are primarily manifested in the main phase. On the other hand, differences in the nature of the trailing CME are reflected in the recovery phase. The following discussion explores these significant impacts and their connections to the in situ signatures.
Figure 8. The Dst indices of all simulated cases in the ensemble cases 1–16, at three longitudes at 1 au. Each panel in (a) shows the time series of the Dst index for different cases. The values of "Min" indicate the minimum Dst value during the event for each longitude, while "Sum" represents the integrated Dst index over time. The subplots (b) at the bottom compare the Dst indices at 0° longitude of Case 0 (the single-CME case), with the cases having 45° and 0° tilt between the CMEs.
Download figure:
Standard image High-resolution image5.1.1. Main Phase
The onset of the Dst main phase begins with the arrival of the first shock at 1 au. Figure 8 illustrates the complex variations among the 16 cases, highlighting the different starting and ending times of the main phase. The onset time variation primarily depends on the ambient SW conditions, which remain constant across all cases, resulting in similar onset times for different cases at the same longitude. However, in scenarios where shock–shock interactions occur, deviations from the initial onset times are observed. Since the shock first impacts the spacecraft at +10° longitude and no shock–shock mergers occur at +10° in any of the cases, the main-phase starting time is identical for the green profile across all cases. This timing aligns with the arrival of the first shock (∼20:00 hr on 2023 May 13).
Similar to +10° longitude, the two shocks arrive sequentially at 0° longitude at 1 au without merging in any of the cases. Both locations exhibit a two-dip profile, where the first dip is associated with the arrival of the first shock and the second dip begins with the arrival of the second shock. In the orange profile, the first Dst drop is very small (around 20:00 UT on May 13) and recovers almost fully to the pre-storm level within a few hours, just before the second shock arrives at about 12:00 UT on May 14. Depending on the strength of the second shock, the Dst value then drops again, reaching a minimum either more rapidly or gradually. A similar trend is observed for the blue profile, with the main difference being that it takes longer for Dst to recover to pre-storm levels before the arrival of the second shock. This variation is primarily due to the Bz profiles at these two locations, as shown in Figure 13. In the orange profile, the negative Bz quickly (∼4 hr) turns positive, whereas at 0° longitude, it remains negative for almost 7 hr.
Unlike the orange and blue profiles, the Dst main-phase profiles at +10° show only a single dip in all cases. In LD cases, this dip features two distinct slopes: an initial gradual decline followed by a sharper fall. For HD cases, there is a single sharp decline to the global minimum, representing the shock–shock merger and indicating that the CME–CME interaction at this longitude is in its fourth stage. Despite the sharpest decline occurring at this location, the minimum Dst values do not always correspond to this longitude. Interestingly, this is especially not true for HF cases without tilt, where the initial magnetic flux of CME2 is greater. In these cases, the minimum Dst value is seen at 0° (blue line) rather than at +10° (green line). Conversely, in LF cases without tilt, the minimum Dst value appears in the green (+10°) profile. This trend is intriguing, because the interaction is most prominent along the +10° longitude. Yet, an increase in the initial magnetic flux of CME2 leads to higher Dst values along this longitude.
There are also some peculiar trends in the main phase corresponding to the initial properties of CME2. The subplots of Figure 8(b) demonstrate clear differences between the HD and LD cases, showing a trend similar to that observed in Figure 5. The divergence between these cases begins around 15:00 hr on May 14, with the arrival of the trailing shock, imitating the differences shown in the strength of the shocks in Figure 3(b). Notably, by the time Dst reaches its global minimum, the temporal gap between the HD and LD cases further widens, with HD cases reaching their minimum Dst value before the single-CME case.
Additionally, cases with and without relative tilt exhibit significant differences. In most cases, both the cumulative Dst and minimum Dst values are higher when there is a relative tilt between the CMEs compared to when there is none. The primary reason for this is the change in orientation of the magnetic field of CME2, which should ideally enhance the effect along −10° and decrease it along +10°, while remaining the same at 0°. However, due to the presence of SW and prolonged interaction with CME1, this trend deviates slightly from the ideal scenario. Figure 13 shows the Bz values for all cases, where the minimum Bz values exhibit a mixed trend along −10°, 0°, and +10° longitudes with changes in tilt. However, the cumulative duration of negative Bz is consistently longer for +10°. Additionally, another noticeable difference is in the slope of the Dst fall, which is steeper for HD cases compared to LD cases.
5.1.2. Recovery Phase
In an ideal single-CME storm, the recovery phase is smooth and continuous, with the Dst index value generally increasing following an exponential trend and gradually returning to the pre-storm level (as in Equation (A3)). Any deviations or additional fluctuations from this ideal trend can indicate the influence of a second CME and subsequent SW. Figure 8(b) showcases that among the 16 ensemble cases, some exhibit significant deviations, others show minor variations, and a few have changes that are almost negligible.
The HD cases exhibit significant deviations from the idealized scenario of the Dst recovery phase. Notably, scenarios without relative tilt between CME1 and CME2 emphasize these deviations more clearly (see Figure 8). In cases 5, 7, 13, and 15, a discontinuity is observed in the Dst index increase across all three profiles (orange, blue, and green), resulting in the formation of a recovery phase plateau. These interruptions, while not affecting the minimum Dst value, significantly prolong the overall recovery time, delaying the return to pre-storm Dst levels. The mentioned HD cases demonstrate notably longer recovery phases compared to their LD counterparts. For instance, by May 16, the Dst index had almost recovered to 0 nT for cases 3 and 11 (LDHF0), whereas for cases 7 and 15 (HDHF0), the Dst index remained near −50 nT.
The recovery phase plateau can be attributed to fluctuations in the southward magnetic field, as southward interplanetary magnetic field (IMF) excursions drive the Dst down before recovery can resume. In the Bz profile (see Figure 13), such fluctuations are noticeable after approximately 18:00 hr on May 14 for HD cases without tilt. These fluctuations in the Bz profile are mirrored by similar, more pronounced fluctuations in the in situ speed profile. As discussed in Section 4.1.3, these fluctuations result from the reverse shock formed by the collision of CME2 with CME1. The propagation of this reverse shock through CME2 creates complex patterns of alternating compressed and rarefied regions, leading to the ripples observed in the in situ profiles. Consequently, these ripples extend the Dst recovery phase by forming a plateau, significantly delaying the return to pre-storm levels.
Apart from the major deviations from the idealized scenarios, many cases showcase minor or no deviations. For example, the blue profile in cases with tilt shows slight deviations; in cases 6 and 14, there is a break point, and in other cases, the profile does not increase smoothly but rather with some disruptions. Notably, there is no significant flipping in the Bz profile after reaching the global minimum in the Dst profile around May 15 for these cases. Interestingly, although there are a few break points around May 15 in the speed profile, the absence of flipping in the Bz profile prevents the formation of any plateau. In other cases, such as 3 and 11, the blue profile closely follows the idealized scenario. Similarly, the orange profile exhibits an ideal recovery phase in almost all tilt cases. In these scenarios, there is neither directional flipping in the Bz profile nor any break points in the speed profile, resulting in a smooth, continuous function.
5.2. Minimum Dst Index
Dst is a measure of the storm-time ring current, and the minimum value of Dst reached during a storm is routinely used as a proxy for storm intensity (J. E. Borovsky & Y. Y. Shprits 2017 and references therein). Although it is by no means a complete characterization of storm-time activity, we use this index as a quantifier of the storm intensity—specifically, the minimum values of the estimated Dst indices at 1 au. To identify trends accurately, we have grouped the cases into pairs, where each pair differs by only one parameter: the initial density, speed, flux, or tilt of CME2. This approach allows us to clearly analyze the effect of variations in these properties on the geo-effectiveness of CME–CME interactions.
5.2.1. Density
Figure 9 illustrates the minimum Dst values for LD and HD cases across three different longitudes: −10°, 0°, and +10°. The percentage differences (nearest integer of ) between paired cases highlight some significant trends. At 0° (panel (a2)) and +10° (panel (a3)), HD cases consistently show lower minimum Dst values compared to LD cases, with percentage differences ranging from 42% to 70% at 0° and 18% to 129% at +10°. This indicates that higher initial densities tend to exacerbate the severity of geomagnetic storms at these longitudes. This trend seems intuitive since a higher initial density in CME2 leads to a stronger trailing shock and higher in situ speed and density, which in turn would lead to a lower Dst index. However, at −10° (panel (a1)), the trend is reversed; HD cases exhibit higher minimum Dst values compared to LD cases, with percentage differences ranging from −8% to −23%. Although there is a significant increase in in situ speed at −10°, the in situ density does not show a major increment, possibly because the trailing shock has to cover a much larger radial distance in an overexpanded region of CME1. Additionally, when this second shock arrived, the Bz profile was not in the southward direction as it was along the 0° and +10° longitudes. Due to this combined in situ configuration, the effective Dst minimum became higher.
Figure 9. Histogram plots of the minimum Dst value corresponding to the change in initial density ((a1)–(a3)), speed ((b1)–(b3)), tilt ((c1)–(c3)), and magnetic flux ((d1)–(d3)), at three longitudes at 1 au.
Download figure:
Standard image High-resolution image5.2.2. Speed
At −10° (panel (b1)), the differences between the LS and HS cases are minimal, with percentage changes ranging from −11% to 2%. This suggests that the initial speed has a relatively minor impact on the severity of geomagnetic storms along this overexpanded CME1 region. In contrast, at 0° (panel (b2)), HS cases consistently exhibit lower minimum Dst values compared to LS cases, with percentage differences ranging from 7% to 15% and an average change of 11%. This potentially indicates that higher initial speeds of CME2 results in a more geo-effective configuration at this longitude. At +10° (panel (b3)), the trend is less consistent (in six out of eight cases), with percentage differences varying from −2% to 18% and an average change of 5%. Despite this variability, HS cases generally lead to lower minimum Dst values (in 18 out of 24 cases), suggesting a trend toward more severe storms with increased speeds. These findings demonstrate that while the influence of the initial speed is significant at 0° and somewhat at +10°, it is relatively minor at −10°.
5.2.3. Tilt
Like the initial density and speed, the effect of the CME2 tilt on the minimum Dst values also shows distinct patterns across the three longitudes. With an average percentage difference of 3%, ranging from −2% to 6%, the Dst minimum was lower for six out of eight tilt cases along −10° longitude (panel (c1)). At 0° (panel (c2)), the tilt's effect is more varied, with percentage differences ranging from –5% to 28% and an average change of 7%, showing lower Dst minimum values for tilted cases in five out of eight instances. The most pronounced effect is observed at +10° (panel (c3)), where the differences are consistent and substantial, ranging from 32% to 128%, with an average decrease of 81%. This significant impact at +10° highlights how the tilt in CME2, which alters the magnetic field orientation, can greatly intensify the geomagnetic storm along one direction. Ideally, the Dst minimum should have consistently increased in the opposite direction (+10°), but the nonuniform deformation of CME1 due to inhomogeneous ambient SW causes the Dst values to deviate from this expected trend.
5.2.4. Magnetic Flux
The increase in the initial magnetic flux of a CME results in an increase in its magnetic field strength. In an ideal isolated flux-rope scenario, this enhancement would typically lead to a lower Dst minimum upon the CME's interaction with Earth's magnetosphere. However, for CME–CME interactions in the presence of a realistic nonuniform ambient SW, the outcome can differ significantly. This is evident in Figure 9. At −10° (panel (d1)), the differences between the low- and high-magnetic-flux cases are relatively minor, with percentage changes ranging from 2% to 12% and an average difference of 5%. This consistent trend of lower Dst minimum for higher initial magnetic flux suggests that magnetic flux does impact the severity of geomagnetic storms, albeit slightly at this location. At 0° (panel (d2)), the impact of the magnetic flux is more pronounced, with percentage differences ranging from −2% to 36% and an average change of 13%. The trend is consistent, with one exception that has the lowest percentage change. Combining the results from −10° and 0°, the trend is clear: higher magnetic flux leads to lower Dst minimum values in 15 out of 16 cases. However, at +10° (panel (d3)), the trend is reversed in seven out of eight cases; high-magnetic-flux cases exhibit higher minimum Dst values compared to low-magnetic-flux cases, with percentage differences ranging from −46% to 2% and an average increase of −16%. It is important to emphasize that this trend reversal occurs along the longitude where the interaction has been strongest. This potentially indicates that higher magnetic flux in CME2 may lead to greater magnetic flux dissipation in strong CME–CME interaction regions, reducing the geo-effectiveness of CME–CME interactions at this longitude.
5.3. Cumulative Dst
We use the cumulative Dst value, representing the summation of the Dst index until it returns to pre-storm levels, to assess the overall impact of the simulated geomagnetic storm event. By considering the cumulative impact, and not just the minimum value of Dst, we can compare the overall intensity of events with different durations (S. Lotz & P. Cilliers 2015). Combined with the Dst minimum, this metric encapsulates both the intensity of the storm and its recovery characteristics, offering a more complete picture of the storm's effect on the Earth's magnetosphere. Similar to the previous subsection, we have used a pair-based analysis to identify trends in the effects of the initial properties of CME2.
5.3.1. Density
The histograms in Figure 10 illustrate the significant impact of the initial density on the cumulative Dst values. Panel (a1) shows the cumulative Dst index values for −10° longitude. The differences between the LD and HD cases are substantial, with percentage changes ranging from −79% to 107% and an average change of −29%. This trend of higher initial densities resulting in lower cumulative Dst values is observed in six out of eight cases, indicating a general reduction in geomagnetic impact at this longitude, consistent with the trend observed in the minimum Dst. At 0° (panel (a2)), HD cases exhibit consistently higher cumulative Dst values compared to LD cases, with percentage differences ranging from 33% to 246% and an average increase of 109%. At +10° (panel (a3)), the differences are even more pronounced, with percentage changes ranging from 28% to 2327% and an average increase of 731%. This increasing trend is observed in all eight cases at 0° and +10°, underscoring the substantial enhancement in storm duration due to the higher initial densities of CME2. These findings demonstrate that the initial density of CME2 plays a crucial role in determining the cumulative geomagnetic impact, with the most significant effects observed at 0° and +10°, and a complex behavior at −10°.
Figure 10. Histogram plots of the cumulative Dst values corresponding to the change in initial density ((a1)–(a3)), speed ((b1)–(b3)), tilt ((c1)–(c3)), and magnetic flux ((d1)–(d3)), at three longitudes at 1 au.
Download figure:
Standard image High-resolution image5.3.2. Speed
At −10° (panel (b1)), the cumulative Dst values show a wide range of percentage changes, from −46% to 47%, with an average change of −16%. This variability highlights that higher initial speeds tend to reduce the cumulative geomagnetic impact at this location, though the trend is opposite to what was observed in the minimum Dst, and the effect is not uniform. In contrast, at 0° (panel (b2)), the cumulative Dst values for HS cases exceed those of LS cases, with percentage changes spanning from −7% to 51% and an average increase of 16%. Here, seven out of eight cases follow this pattern, consistent with the trend observed in the minimum Dst. At +10° (panel (b3)), the differences are more subtle, with percentage changes ranging from −9% to 23% and an average change of 9%. This pattern appears in six out of eight cases, suggesting a mild tendency for higher speeds to amplify the cumulative Dst values. These observations indicate that the impact of CME2's initial speed on the storm duration and intensity varies with longitude, showing enhancement at 0° and +10° but reduction at −10°.
5.3.3. Tilt
The impact of tilt between CMEs shows a relatively more consistent trend. For −10°, the cumulative Dst values decrease, they show mixed behavior at 0°, and increase at +10°. At −10° (panel (c1)), the high-tilt cases have percentage changes ranging from −86% to 6%. This trend is observed in seven out of eight cases, with an average change of −36%, opposed to the general observation in minimum Dst. Moving to 0° (panel (c2)), the effect of tilt becomes inconsistent. Here, percentage changes vary from −16% to 170%, with an average change of 34%. The trend is followed in five out of eight cases, indicating a mixed influence of tilt on cumulative geomagnetic impact, and it is not as pronounced as at −10°. In contrast, at +10° (panel (c3)), the high-tilt cases dramatically increase the cumulative Dst values, with percentage changes ranging from 32% to 2402% and an average increase of 697%. This overwhelming trend is observed in all eight cases, highlighting a substantial enhancement in geomagnetic storm duration and intensity due to tilt at this longitude. This demonstrates that CME2's tilt has a variable influence on the cumulative geomagnetic impact, with a significant reduction at −10°, moderate variability at 0°, and immense enhancement at +10°.
5.3.4. Magnetic Flux
Among the three longitudes, only the cumulative Dst values at 0° show a consistent trend, while the ±10° longitudes exhibit mixed behavior with the increasing magnetic flux of CME2. This inconsistency contrasts with the statistical trends observed in the minimum Dst. At −10° (panel (d1)), the percentage changes range from −46% to 362%. Decreases are observed in five out of eight cases, but the average change is +56%, reflecting minor decrements and significant increments. Similarly, at +10° (panel (d3)), the results are highly variable, with percentage changes ranging from −41% to 184% and an average increase of 22%. Decreases occur in five cases, while increases are seen in three out of eight cases. In contrast, at 0° (panel (d2)), the impact of higher magnetic flux is consistent and more pronounced, with percentage changes spanning from 15% to 156% and an average increase of 67%. This trend is observed in all eight cases, indicating a strong correlation between increased magnetic flux and enhanced geomagnetic storm duration and intensity.
6. Summary
In this ensemble study, we have utilized the SWASTi framework to conduct MHD simulations of 16 different scenarios of CME–CME interaction. The simulations employed a flux-rope CME, propagating within data-driven realistic SW conditions. The chosen SW conditions correspond to CR period 2270, with the projected trajectory of the CMEs passing through an SW SIR. This unique setup implies that all CME–CME interactions in this study are significantly influenced by the in-path SIR, effectively making it a CME–CME–SIR interaction scenario. Below are brief discussions and conclusive remarks on the topics covered in this work:
Role of SW. Figure 1 clearly illustrates this situation and its implications. In all ensemble cases, the upper flank of CME1 overexpands compared to the lower flank. This differential expansion occurs because the upper flank, situated along the fast stream, experiences greater pressure gradients, leading to more expansion and faster movement than the bottom flank. The inhomogeneity in the ambient SW results in an asymmetrical radial width of CME1. This variability makes the CME–CME collision nonuniform across the interaction surface.
Shock Evolution. We thoroughly investigated the dependency of the shock evolutionary stages proposed by N. Lugaz et al. (2005) on the initial properties of CME2. Our study revealed that the evolution of these stages varied across different longitudes, primarily due to the nonuniform radial extension of CME1. This finding highlights that the shock-based classification of CME–CME interaction stages is not universally applicable to the entire structure but rather a localized phenomenon.
Impact on CME1. By comparing ensemble cases with the single CME1 simulation, we found some peculiar trends in the kinematic, magnetic, and structural properties:
- 1.Kinematic. Due to the collision, CME1 gained 9%–36% in radial momentum and 15%–65% in KE by the time it reached 1 au. The temporal evolution showed similar patterns, with an initial rising phase lasting about 10 hr, followed by a diminishing phase. The amount of gain and the duration of the rising phase were most influenced by CME2's initial density.
- 2.Magnetic. CME1's magnetic properties showed less significant changes compared to its kinematic properties and followed a different evolution pattern. It increased by 1%–3% only in HD cases. We observed an initial increase in ME up to 20–25 hr, followed by a decrease due to magnetic field dissipation. This behavior is consistent with G. J. Koehn et al. (2022), given that the CMEs had the same chirality.
- 3.Structural. The longitude (+10°) where CME1 interacted with both the SIR from the front and CME2 from behind showed the highest compression—more than twice than at the longitude (−10°) without SIR interaction. This indicates that the SIR significantly enhances the leading CME's radial compression. Overall, CME2's initial density was observed to be a key factor in determining the interaction's impact on CME1.
Mixing. We also analyzed the mixing of CMEs during their interaction in the heliosphere and found that the amount of mixing varies significantly, depending on the initial conditions of the trailing CME. Enhanced mixing was observed along the bottom flank, where the interaction strength is higher due to the presence of the SIR ahead of the leading CME, again highlighting the impact of inhomogeneity in the ambient SW.
Reverse Shock. Another noteworthy phenomenon observed in the CME–CME interaction was the formation of reverse shocks in cases of strong interaction. Similar observations were reported by N. Lugaz et al. (2005) in their MHD simulation of two identical CMEs interacting in a simple axisymmetric SW setup. Additionally, D. Trotta et al. (2024) recently observed such a reverse shock using Solar Orbiter data. We found that these shocks can originate from multiple locations due to the nonuniform interaction between CME1 and CME2 along different longitudes. As these reverse shocks propagate inside CME2, they create a complex pattern of alternating compressed and rarefied regions, causing ripples or fluctuations in the in situ data (see Figure 3). These ripples influence the geo-effectiveness of the CME–CME structure, notably extending the overall recovery phase and delaying the return to pre-storm Dst levels.
Geo-effectiveness. We conducted a statistical study of the minimum and cumulative Dst index values for the ensemble cases to identify trends related to CME2's initial properties. Along the strong interaction region (+10°), the minimum Dst value decreased with the increased initial density, tilt, and speed of CME2, with average changes of 66%, 81%, and 6%, respectively, indicating higher geo-effectiveness. Conversely, the minimum Dst value increased by an average of 19% with higher initial ME, suggesting greater magnetic dissipation and lower geo-effectiveness. Trends were less consistent at 0° and −10°. Overall, an increase in any initial property of CME2 mostly leads to stronger (72% of cases) and more prolonged (63% of cases) storms.
It is important to emphasize that this ensemble study was conducted using an ideal MHD setup. Consequently, a quantitative study of magnetic dissipation in CME–CME interactions lies beyond the scope of this work. Additionally, the ambient SW conditions were consistent across all cases, introducing a bias toward specific ambient conditions. Therefore, the conclusions drawn are particularly relevant to the scenario of CME–CME–SIR interaction. We have also not considered the role of initial flux-rope orientation (e.g., chirality and polarity) in this study, which can have a considerable impact on geo-effectiveness (G. J. Koehn et al. 2022). Moreover, the CME insertion method used here is not fully conventional, and a more organic leg-cutting approach is needed to improve simulation fidelity. In our future work, we aim to include nonideal MHD effects to explore such interactions in greater depth, especially to investigate the formation of reverse shocks and their dependency on CME properties. This approach will provide a more comprehensive understanding of the underlying physical processes that can enhance the geo-effectiveness of CME–CME interaction events.
Acknowledgments
We thank the anonymous referee for valuable suggestions, which enhanced the content of this manuscript. P.M. gratefully acknowledges the support provided by the Prime Minister's Research Fellowship. Much of the work in this paper was conducted while P.M. was hosted by S.L. at SANSA in Hermanus (South Africa), funded by the SCOSTEP Visiting Scholar (SVS) program. We are grateful for funding from the SVS program and hosting by SANSA. B.V. and D.C. acknowledge the support from the ISRO RESPOND grant number ISRO/RES/2/436/21-22. Furthermore, the work of D.C. is supported by the Department of Space, Government of India.
The GONG synoptic magnetogram maps used can be freely obtained from https://gong.nso.edu/data/magmap/crmap.html. The OMNI data are taken from the Goddard Space Flight Center, accessible at https://spdf.gsfc.nasa.gov/pub/data/omni/. The PLUTO code used for the MHD simulation can be downloaded free of charge from http://plutocode.ph.unito.it/.
Appendix A: Empirical Relation of Dst
T. O'Brien & R. L. McPherron (2000) proposed the following empirical relations for computing the Dst index based on the plasma properties at the Sun–Earth L1 point:
Here, Dst* represents the pressure-corrected Dst index, accounting for magnetopause current contamination, with constants b = 7.26 and c = 11. The parameter Q denotes the rate of energy injection into the ring current, while τ represents the decay time of the ring current, influenced by particle loss to the atmosphere. The variables V and Pdyn are the plasma speed and dynamic pressure, respectively, and Bz is the Z-component of the magnetic field in geocentric solar magnetospheric coordinates. Dst* is used to perform time integration, and the model output Dst is calculated from Equation (A5). Under usual circumstances, the initial value of the estimated Dst is set to the last measured value before the prediction is made (T. O'Brien & R. L. McPherron 2000). However, since we are dealing with simulated CMEs, we cannot have observed initial values for the Dst. Therefore, we set the "initial level" of Dst at 0 nT, as Dst was designed for the quiet-time reference level to be zero (M. Sugiura & T. Kamei 1991).
Although the efficiency of the above empirical Dst relation has been extensively demonstrated by T. O'Brien & R. L. McPherron (2000), we sought to verify its performance for significant geo-effective events in recent years. To test this relation, we compared the Dst values derived from the model with OMNI 1 hr data. Specifically, we examined CME events occurring during CRs 2165, 2194, and 2270, which included five interacting CMEs, two interacting CMEs, and one single CME, respectively. For these comparisons, the initial Dst values required for the model were set to match the observed Dst values at the initial time for the CR.
Figure 11 presents the comparison between the modeled and observed Dst values. Subplots (a1) and (a2) depict the observed in situ plasma properties at L1 (speed, density, and IMF Bz component). The estimated Dst, based on these values, is broadly accurate and captures most of the storm's features, such as the momentary rise in Dst due to a short-period northward IMF on 2023 June 1 (see Figure 11(a3)). The onset of the initial phase of Dst and the duration of the main phase in the model output also match nicely for all three CRs. However, some finer structures are missed, such as the sudden commencement on 2017 August 18 (panel (b)), and the model shows some discrepancies in the magnitude of the storm's recovery phase.
Figure 11. Comparison of observed Dst and the estimated values as described in Equations (A1)–(A5). The (a1), (b1), and (c1) panels show the observed in situ SW speed, density, and Bz values at the Sun–Earth L1 point for CR2270, CR2194 and CR2165, respectively. The (a2), (b2), and (c2) panels show the observed vs. estimated Dst values for these three CRs, along with their difference.
Download figure:
Standard image High-resolution imageThe statistical results are promising, with Pearson correlation coefficient values ranging from 0.92 to 0.94 and rms error values between 18 and 27 nT, corresponding to an error margin of roughly 9%–17%. This strong agreement indicates that the empirical relation is reliable for comparative studies between events, which is the primary application in this work for comparing the Dst values across different ensemble cases.
Appendix B: Interaction Scenario
The nature of the CME–CME interaction scenario undertaken in this study is demonstrated in Figure 12. It showcases a unique interaction scenario, complicated by the presence of SIR ahead of the leading CME. In the subplots, the trailing CME is catching up to the leading CME, which has already encountered the SIR. This configuration creates a dynamic environment where multiple structures—two CMEs and the SIR—interact, leading to a complex scenario. HD regions at the boundaries of both CMEs and within the SIR are clearly visible. This particular scenario underscores the complexity of interacting SW structures, with the scaled density plots offering a detailed view of the varying intensities within the system. The corresponding temperature plot has been shown in Figure 2.
Figure 12. The panels showcase the scaled density (in log10 scale, N cm−3) for the considered CME–CME–SIR interaction scenario in the inner heliosphere. Panels (a1)–(a4) represent the temporal evolution of the scale density for the case LSLDLF0, while panels (b1)–(b4) depict the scenario for the case LSHDLF0.
Download figure:
Standard image High-resolution imageAppendix C: In Situ Profile at 1 au
In this section, we present the in situ profiles observed by three virtual spacecraft at 1 au along 0° and ±10° longitudes for all the 16 ensemble cases. Figure 13 shows the density and southward component of the magnetic field (Bz ) profiles, for the period from 2023 May 13 at 9 UT to May 15 at 14 UT, to highlight the most relevant structures. To keep the relevant peaks in the upper half of the subplots, we have inverted the Bz profile, with negative values shown upward and positive values downward. The key aspects of the features in these in situ profiles have been discussed in Section 5.1.
Figure 13. These plots illustrate the southward magnetic field (Bz ) at the location of the three virtual spacecraft used in this study, showcased at −10° (orange), 0° (blue), and +10° (green) longitudinal positions. The entire set of 16 cases within the CME–CME interaction ensemble is represented here.
Download figure:
Standard image High-resolution image












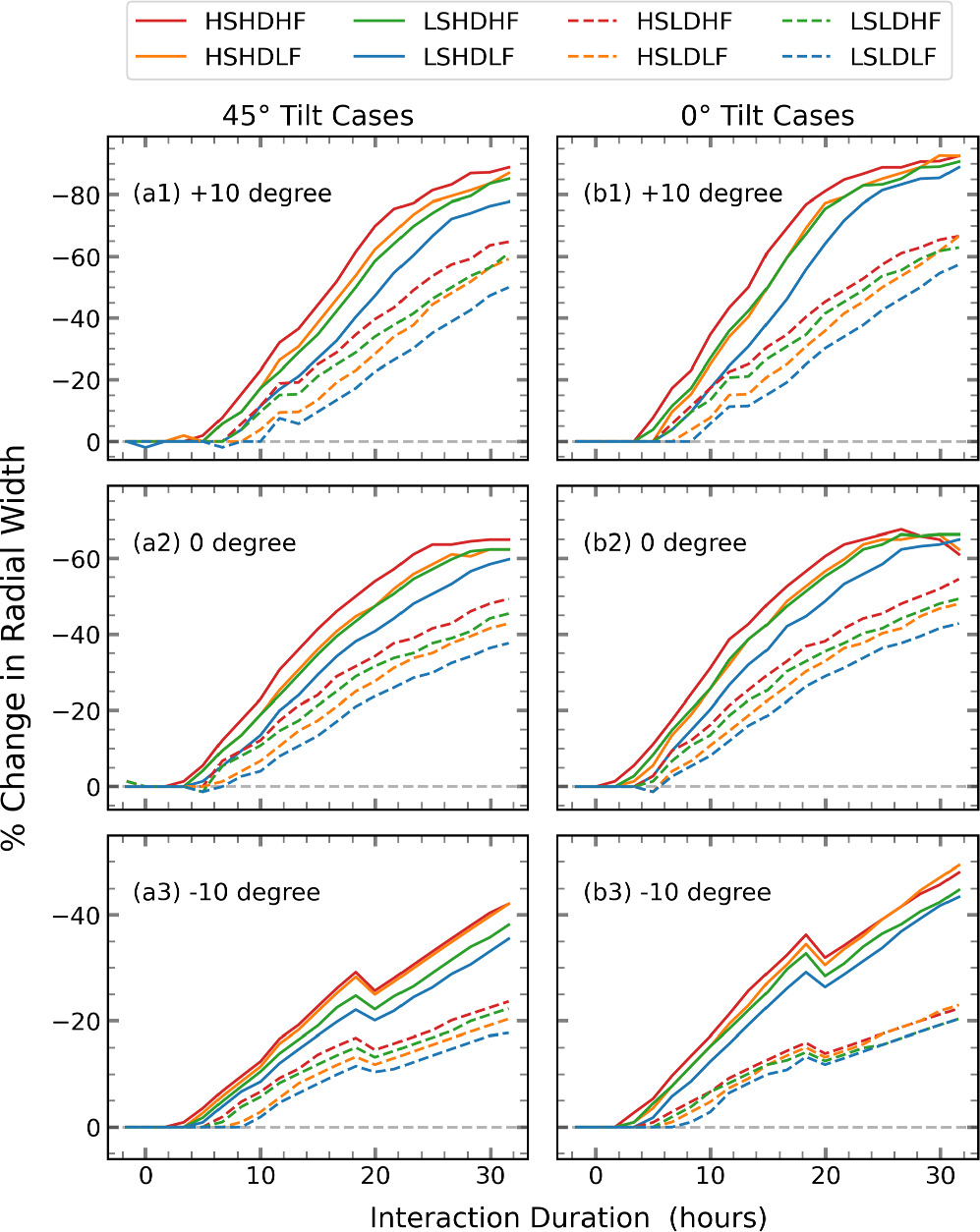



















![$100\cdot \left[\tfrac{\mathrm{HD}-\mathrm{LD}}{\mathrm{LD}}\right]$](https://content.cld.iop.org/journals/0004-637X/976/1/126/revision2/apjad8084ieqn18.gif)









