Generalized variational inclusion: graph convergence and dynamical system approach

1.   Introduction

The theory of variational inequalities (VIs) was initially originated from variational principles for investigating partial differential equations ^[31]. It is a dynamic tool for unifying and studying equilibrium problems. It has been recognized as a potential and compelling approach for exploring and analyzing nonlinear problems of science and engineering, complex boundary value problems, models of economics, and transportation and operations research by reformatting them as a VI. Since its rise, this theory has been augmented by diverse techniques and methodologies.

Among the succeeding expansions, one of the prominent, most fruitful and worthwhile generalizations of VI is variational inclusion. The variational inclusion problem plays a crucial role in the formulation of mathematical models of various real-life problems with practical implications across diverse disciplines. The monotone inclusion problem (MIP) is to discern an element $\theta^{*}\in \mathbb H$ so that

where ${\mathbb H }$ is a real Hilbert space, $\psi: {\mathbb H}\to {\mathbb H }$ is a single-valued monotone operator, and $\varphi: {\mathbb H}\to 2^{\mathbb H}$ is a maximal monotone operator. We indicate the solution set of the MIP (1.1) by $(\varphi+\psi)^{-1}(0)$. Variational inclusions have been implemented to tackle numerous equilibrium and optimization problems including image processing, image deblurring, convex minimization, DC programming, split feasibility, fixed point and VI problems; see ^{[1,9,12,17,21,23,27,28,29,33]}. Applicability and usefulness of variational inclusions have captivated the attentiveness of numerous scholars in a short span of time. As of now, a number of approaches have been carried out for figuring out the problem. One of the fundamental approaches to deal with these problems is to reduce the inclusion problem into an analogous fixed point problem by employing the technique of resolvent.

In recent times, for the sake of generalizing VIs and inclusions, the researchers have generalized the conception of monotone and accretive mappings such as $m$-accretive mappings ^[20] as an allied approach for maximal monotone, maximal $\eta$-monotone and $\eta$-subdifferential mappings. In this sequel, the concept of $H$-monotone mapping was incepted by Fang and Huang ^[15] in Hilbert spaces, and later they further coined an analogous notion in Banach spaces named $H$-accretive mappings ^[16]. In 2008, Zou and Huang ^[35] enriched the literature by defining the $H(\cdot, \cdot)$-accretive operator in Banach spaces. Using these generalized monotone and accretive mappings, authors have examined numerous variational inclusions by implementing the resolvent operators. Moreover, the notion of the $H(\cdot, \cdot)$-co-coercive mapping was set forth by Ahmad et al. ^[3]. This concept was further extended by defining $H(\cdot, \cdot)$-co-monotone mapping ^[4], which is the combination of symmetric co-coercive and monotone mapping. An analogous conception was studied in Banach spaces and named as $H(\cdot, \cdot)$-co-accretive mapping ^[5], which is the combination of symmetric co-coercive and accretive mapping. The researchers explored some properties of these operators and applied them to investigate a number of variational inclusions. Subsequently, a great deal of work has gone into examining variational inclusion problems involving generalized monotone and accretive mappings using the graph convergence. Li and Huang ^[22] brought the idea of graph convergence for $H(\cdot, \cdot)$-accretive mappings and shown that it is homologous to the resolvent operator convergence Further, Ahmad et al. ^[2] utilized the conception of graph convergence to examine a system of generalized variational inclusions involving $H(\cdot, \cdot)$-co-accretive mapping. For a detailed literature on graph convergence, we refer to ^[6,7,10,32].

Since the equilibrium point of the dynamical system leads to the solution of the corresponding VI and inclusion problem, dynamical systems represent cohesive, all-encompassing frameworks of VIs and inclusions as their equilibrium points serve as solutions to these problems. Thus, all the problems whose mathematical models can be solved using VIs can also be examined in the general framework of the dynamical systems. This characteristic has drawn the attention of researchers to study dynamical systems associated with VI and inclusion problems. One can transform the model of VI or inclusion problems into a fixed point problem by implementing the novel resolvent or projection operator, and such transformations allow us to suggest dynamical systems. Dynamical systems directly or indirectly appear in several useful areas encompassing celestial mechanics, environmental studies, financial forecasting, modeling of neuroscience, etc., and allow us to describe the trajectories of physical process and real-world problems before achieving the steady state. For further applications of the dynamical systems, see ^{[13,14,18,24,25,26]}.

Inspired and persuaded by the above stated work, in this study, we investigate a generalized variation inclusion problem. We define the resolvent operator for generalized $\eta$-co-monotone mapping and estimate its Lipschitz constant. Further, its relationship with the graph convergence is accomplished. An Ishikawa type iterative algorithm is structured and analyzed to obtain the common solution of the generalized variational inclusion and the set of fixed points of a total asymptotically non-expansive mapping by employing the novel implication of graph convergence. Moreover, we construct a generalized resolvent dynamical system associated to the generalized variational inclusion and discuss some of its attributes. Further, we investigated the considered generalized variation inclusion problem by implementing the generalized resolvent dynamical system. Also, the theoretical results are verified by illustrative examples.

2.   Relevant concepts and auxiliary results

Now onward, $\mathbb H$ is assumed to be a real Hilbert space endued with norm $\|\cdot\|$ which induces the metric $d$ and inner product $\langle \cdot, \cdot\rangle$. The collection of all closed and bounded subsets of $\mathbb H$ is signified as $CB({\mathbb H})$.

Definition 2.1. Let $\eta:{\mathbb H}\times {\mathbb H} \to {\mathbb H}$ be a single-valued mapping. A mapping $\psi:{\mathbb H} \to {\mathbb H}$ is referred to as

(i) $\eta$-monotone if

(ii) $\rho$-strongly $\eta$-monotone if $\exists \rho > 0$ so that

(iii) $\varpi$-Lipschitz continuous if $\exists \varpi > 0$ so that

(iv) $\zeta$-expansive if $\exists \zeta > 0$ so that

The following lemma is a crucial instrument for carrying out the adopted scheme.

Lemma 2.1. ^[34] Let $\{p_{k}\}_{k = 1}^{\infty}$ be a nonnegative real sequence and $\{q_{k}\}_{k = 1}^{\infty}$ be a real sequence in [0, 1] with $\sum_{k = 0}^{\infty}q_{k} = \infty$ fulfilling the following inequality:

where $\tau_{k}\geq 0, \forall k\geq 0$ and $\lim_{k\to\infty}\tau_{k} = 0$. Then $\lim_{k\to \infty}p_{k} = 0$.

2.1.   Generalized $\eta$-co-monotone operator

Definition 2.2. Let $\eta, \Phi:{\mathbb H}\times {\mathbb H} \to {\mathbb H}$ and $\psi, \varphi: {\mathbb H} \to {\mathbb H}$ be the single-valued mappings. Then $\Phi(\cdot, \cdot)$ is known as

(i) $m$-mixed Lipschitz continuous with respect to $\psi$ and $\varphi$ if $\exists m > 0$ such that

(ii) $\eta$-co-coercive with respect to $\psi$ if $\exists \kappa^{'} > 0$ such that

(iii) relaxed $\eta$-co-coercive with respect to $\varphi$ if $\exists \kappa^{''} > 0$ such that

(iv) symmetric $\eta$-co-coercive with respect to $\psi$ and $\varphi$ if $\Phi(\cdot, \cdot)$ satisfies (ii) and (iii).

Definition 2.3. Let $\eta, \Phi:{\mathbb H}\times {\mathbb H} \to {\mathbb H}$; $G, \psi, \varphi: {\mathbb H} \to {\mathbb H}$ be the single-valued mappings and $\Psi:{\mathbb H}\to CB({\mathbb H})$ be a set-valued mapping. Then, $\Phi(\cdot, \cdot)$ is known as mixed $\delta$-strongly monotone with respect to $G$ and $\Psi$, if for some $\omega\in \Psi(\theta), \bar{\omega}\in \Psi(\vartheta)$, $\exists \delta > 0$ such that

Definition 2.4. Let $\eta:{\mathbb H}\times {\mathbb H} \to {\mathbb H}$ and $f, g: {\mathbb H} \to {\mathbb H}$ be the single-valued mappings. A set-valued mapping $M:{\mathbb H}\times {\mathbb H} \rightrightarrows {\mathbb H}$ is known as

(i) $\tau^{'}$-strongly $\eta$-monotone with respect to $f$ if $\exists \tau^{'} > 0$ so that

(ii) $\tau^{''}$-relaxed $\eta$-monotone with respect to $g$ if $\exists \tau^{''} > 0$ so that

(iii) $M(\cdot, \cdot)$ is known as symmetric $\eta$-monotone with respect to $f$ and $g$ if $M(\cdot, \cdot)$ satisfies (i) and (ii).

Definition 2.5. Let $\eta, \Phi:{\mathbb H}\times {\mathbb H} \to {\mathbb H}$ and $\psi, \varphi, f, g: {\mathbb H} \to {\mathbb H}$ be the single-valued mappings. A set-valued mapping $M:{\mathbb H}\times{\mathbb H} \rightrightarrows {\mathbb H}$ is referred to as generalized $\eta$-co-monotone if $\Phi(\cdot, \cdot)$ is symmetric $\eta$-co-coercive with respect to $\psi$ and $\varphi$, $M(\cdot, \cdot)$ is symmetric $\eta$-monotone with respect to $f$ and $g$, and

Note 2.1. Now onward, $M$ is generalized $\eta$-co-monotone means, $\Phi(\cdot, \cdot)$ is $\eta$-symmetric co-coercive with respect to $\psi$ and $\varphi$ with constants $\kappa^{'}$ and $\kappa^{''}$, respectively, and $M(\cdot, \cdot)$ is symmetric $\eta$-monotone with respect to $f$ and $g$ with constants $\tau^{'}$ and $\tau^{''}$, respectively, and satisfies (2.1).

Lemma 2.2. Let $\eta, \Phi:{\mathbb H}\times {\mathbb H} \to {\mathbb H}$ and $\psi, \varphi, f, g: {\mathbb H} \to {\mathbb H}$ be the single-valued mappings. Let $M:{\mathbb H}\times{\mathbb H} \rightrightarrows {\mathbb H}$ be a generalized $\eta$-co-monotone mapping. Let $\psi$ be $\varsigma$-expansive and $\varphi$ be $l$-Lipschitz continuous. Then, for all $\varrho > 0$, the mapping $[\Phi(\psi, \varphi)+\varrho M(f, g)]^{-1}$ is single-valued.

Definition 2.6. Let $\eta, \Phi:{\mathbb H}\times {\mathbb H} \to {\mathbb H}$ and $\psi, \varphi, f, g: {\mathbb H} \to {\mathbb H}$ be the single-valued mappings. Let $M:{\mathbb H}\times{\mathbb H} \rightrightarrows {\mathbb H}$ be a generalized $\eta$-co-monotone mapping. The resolvent ${\mathbb R}^{\eta, \Phi(\cdot, \cdot)}_{\varrho, M(\cdot, \cdot)}:{\mathbb H} \to {\mathbb H}$ is described as

Proposition 2.1. Let $\eta:{\mathbb H}\times {\mathbb H} \to {\mathbb H}$ be a $\pi$-Lipschitz continuous mapping; $\Phi:{\mathbb H}\times {\mathbb H} \to {\mathbb H}$ and $\psi, \varphi, f, g: {\mathbb H} \to {\mathbb H}$ be the single-valued mappings such that $\psi$ is $\varsigma$-expansive and $\varphi$ is $l$-Lipschitz continuous. Let $M:{\mathbb H}\times{\mathbb H} \rightrightarrows {\mathbb H}$ be a generalized $\eta$-co-monotone mapping. Then, ${\mathbb R}^{\eta, \Phi(\cdot, \cdot)}_{\varrho, M(\cdot, \cdot)}:{\mathbb H} \to {\mathbb H}$ is $\Xi$-Lipschitz continuous, where

Proof. For given $\theta, \vartheta\in {\mathbb H}$, it follows from (2.2) that

From (2.3) and (2.4), one can write

For the sake of simplicity, we indicate $\Lambda(\theta) = {\mathbb R}^{\eta, \Phi(\cdot, \cdot)}_{\varrho, M(\cdot, \cdot)}(\theta)$ and $\Lambda(\vartheta) = {\mathbb R}^{\eta, \Phi(\cdot, \cdot)}_{\varrho, M(\cdot, \cdot)}(\vartheta)$, and since $M(\cdot, \cdot)$ is symmetric $\eta$-monotone, then

Invoking symmetric $\eta$-co-coercivity of $\Phi$, $\varsigma$-expansiveness of $\psi$, $l$ and $\pi$-Lipschitz continuities of $\varphi$ and $\eta$, respectively, we attain $\varrho(\tau^{'}-\tau^{''})\|\Lambda(\theta)-\Lambda(\vartheta)\|^{2}\leq\langle\theta-\vartheta, \eta(\Lambda(\theta), \Lambda(\vartheta))\rangle-(\kappa^{'}\varsigma^{2}-\kappa^{''}l^{2})\|\Lambda(\theta)-\Lambda(\vartheta)\|^{2},$ i.e.,

Thus, for all $\theta, \vartheta\in {\mathbb H}$, we obtain $\|\Lambda(\theta)-\Lambda(\vartheta)\|\leq \Xi\|\theta-\vartheta\|$, i.e.,

where, $\Xi = \frac{\pi}{[\varrho(\tau^{'}-\tau^{''})+(\kappa^{'}\varsigma^{2}-\kappa^{''}l^{2})]}$. □

2.2.   Graph convergence

Definition 2.7. The graph of a multivalued mapping $M:{\mathbb H}\times{\mathbb H} \rightrightarrows {\mathbb H}$ is expressed as

Definition 2.8. Let $\eta, \Phi:{\mathbb H}\times {\mathbb H} \to {\mathbb H}$ and $\psi, \varphi, f, g: {\mathbb H}\to {\mathbb H}$ be the single-valued mappings. For $n\geq 0$, let $M_{n}, M:{\mathbb H}\times{\mathbb H} \rightrightarrows {\mathbb H}$ be generalized $\eta$-co-monotone mappings. Then, $\{M_{n}\}_{n = 1}^{\infty}$ is known as graph convergent to $M$, indicated by $(M_{n}\underrightarrow{\mathbb G} M)$ if for each $(f(\theta), g(\theta), \xi)\in Graph(M)$, $\exists\{(f(\theta_{n}), g(\theta_{n}), \xi_{n})\}\in Graph(M_{n})$ so that

Theorem 2.1. Let $\eta, \Phi:{\mathbb H}\times {\mathbb H} \to {\mathbb H}$ and $\psi, \varphi, f, g: {\mathbb H}\to {\mathbb H}$ be the single-valued mappings such that $\Phi(\cdot, \cdot)$ is $m$-mixed Lipschitz continuous with respect to $\psi$ and $\varphi$, and $f, g$ are continuous mappings so that $f$ is $\zeta$-expansive. For $n\geq 0$, let $M_{n}, M:{\mathbb H}\times{\mathbb H} \rightrightarrows {\mathbb H}$ be generalized $\eta$-co-monotone mappings. Then,

Proof. For all $\theta\in {\mathbb H}$ and $\varrho > 0$, suppose that ${\mathbb R}^{\eta, \Phi(\cdot, \cdot)}_{\varrho, M_{n}(\cdot, \cdot)}(\theta)\to {\mathbb R}^{\eta, \Phi(\cdot, \cdot)}_{\varrho, M(\cdot, \cdot)}(\theta).$ Assume that $(f(\theta), g(\theta), \xi)\in Graph(M)$, then

Letting

which turns into

For each $n\geq 0$, take $\xi_{n}\in M(f(\theta_{n}), g(\theta_{n}))$, then (2.10) yields

Invoking the $m$-mixed Lipschitz continuity of $\Phi$, it follows from (2.11) that

Thus, $\|\xi_{n}-\xi\|\leq \frac{m}{\varrho}\|\theta_{n}-\theta\|$. Recalling the hypothesis ${\mathbb R}^{\eta, \Phi(\cdot, \cdot)}_{\varrho, M_{n}(\cdot, \cdot)}(\theta)\to {\mathbb R}^{\eta, \Phi(\cdot, \cdot)}_{\varrho, M(\cdot, \cdot)}(\theta)$, it yields from (2.8) and (2.9) that $\|\theta_{n}-\theta\|\to 0$ and, hence, from (2.12), we acquire $\|\xi_{n}-\xi\|\to 0$ as $n\to \infty$. Accounting the continuity of $f$ and $g$, we deduce $f(\theta_{n})\to f(\theta)$ and $g(\theta_{n})\to g(\theta)$, and so $M_{n}\underrightarrow{\mathbb G} M$.

On the contrary, assume that $M_{n}\underrightarrow{\mathbb G} M$ and choose an arbitrary but fixed $e\in {\mathbb H}$. Since $M(\cdot, \cdot)$ is a generalized $\eta$-co-monotone mapping, $Range[\Phi(\psi, \varphi)+\varrho M(f, g)] = {\mathbb H}$. Then, there exists $((f(\theta), g(\theta)), \xi)\in Graph(M)$ such that $e = \Phi(\psi(\theta), \varphi(\theta))+\varrho \xi$. Since $(f(\theta), g(\theta), \xi)\in Graph(M)$ and suppose $(f(\theta_{n}), g(\theta_{n}), \xi_{n})\in Graph(M_{n})$,

Letting $e_{n} = \Phi(\psi(\theta_{n}), \varphi(\theta_{n}))+\varrho \xi_{n}$, for all $n\geq 0$, adducing the $m$-mixed Lipschitz continuity $\Phi(\cdot, \cdot)$ and making use of (2.7), we acquire

The $\zeta$-expansiveness of $f$ yields

Thus, we deduce from (2.14) and the Definition 2.8 that $\theta_{n}\to\theta$ and $\xi_{n}\to\xi$ as $n\to \infty$. Thus, from (2.13), we infer that ${\mathbb R}^{\eta, \Phi(\cdot, \cdot)}_{\varrho, M_{n}(\cdot, \cdot)}(\theta)\to{\mathbb R}^{\eta, \Phi(\cdot, \cdot)}_{\varrho, M(\cdot, \cdot)}(\theta)$. □

Example 2.1 Let ${\mathbb H} = {\mathbb R^{2}}$ with the usual inner product on ${\mathbb R^{2}}$, i.e.,

Define $\psi, \varphi:{\mathbb R^{2}}\to {\mathbb R^{2}}$ and $\eta, \Phi:{\mathbb R^{2}}\times {\mathbb R^{2}}\to {\mathbb R^{2}}$ by

Then, for any fixed $\varsigma\in {\mathbb R^{2}}$, we find

Thus, $\Phi(\cdot, \cdot)$ is $\eta$-co-coercive with respect to $\psi$ and relaxed $\eta$-co-coercive with respect to $\varphi$, hence $\Phi(\cdot, \cdot)$ is symmetric $\eta$-co-coercive. Next, we estimate the symmetric monotonicity of $M$. Define $f, g:{\mathbb R^{2}}\to {\mathbb R^{2}}$ and $M:{\mathbb R^{2}}\times {\mathbb R^{2}}\to {\mathbb R^{2}}$ by

Then for any fixed $\varpi\in {\mathbb R^{2}}$, we find

i.e., $M(\cdot, \cdot)$ is $\eta$-monotone with respect to $f$ and relaxed $\eta$-monotone with respect to $g$, hence $M(\cdot, \cdot)$ is symmetric $\eta$-monotone. Also, for any $\theta\in {\mathbb R^{2}}$ and $\varrho > 0$,

i.e., $[\Phi(\psi, \varphi)+\varrho M(f, g)]({\mathbb R^{2}}) = {\mathbb R^{2}}, \forall \varrho > 0$. Thus, $M(\cdot, \cdot)$ is a generalized $\eta$-co-monotone mapping. Further, we show that $M_{n}\underrightarrow{\mathbb G} M$. Let

and $\xi_{n} = M_{n}(f(\theta_{n}), g(\theta_{n})) = f(\theta_{n})-g(\theta_{n}) = \big(-\frac{3}{2}\theta_{2}+\frac{2}{n}-\frac{2}{n^{2}}, \frac{3}{2}\theta_{1}+\frac{1}{4}\theta_{2}+\frac{1}{n}-\frac{1}{n^{2}} \big)$. One can observe that

and $\lim\limits_{n\to \infty}\xi_{n} = \lim\limits_{n\to \infty} \big(-\frac{3}{2}\theta_{2}+\frac{2}{n}-\frac{2}{n^{2}}, \frac{3}{2}\theta_{1}+\frac{1}{4}\theta_{2}+\frac{1}{n}-\frac{1}{n^{2}} \big) = f(\theta)-g(\theta) = M(f(\theta), g(\theta)) = \xi$.

Thus, we acquire that $\lim\limits_{n\to \infty}f(\theta_{n}) = f(\theta)$ and $\lim\limits_{n\to \infty}g(\theta_{n}) = g(\theta)$ and $\lim\limits_{n\to \infty}\xi_{n} = \xi$. Hence, $M_{n}\underrightarrow{\mathbb G} M$. Finally, it remains to manifest that $M_{n}\underrightarrow{\mathbb G} M\Leftrightarrow {\mathbb R}^{\eta, \Phi(\cdot, \cdot)}_{\varrho, M_{n}(\cdot, \cdot)}(\theta)\to {\mathbb R}^{\eta, \Phi(\cdot, \cdot)}_{\varrho, M(\cdot, \cdot)}(\theta), \forall \theta\in {\mathbb H}, \varrho > 0.$ Now, for $\varrho = 1$, the associated resolvent operators are estimated as:

and

which yields

Thus, we obtain

3.   Problem formulation and convergence result

In this section, we employ a generalized $\eta$-co-monotone mapping for investigating a general variational inclusion (GVIP). We examine the problem of discerning $\theta\in {\mathbb H}, \omega\in \Psi(\theta)$ so that

where $G, f, g:{\mathbb H}\to {\mathbb H}$ and $M:{\mathbb H}\times {\mathbb H}\rightrightarrows {\mathbb H}; \Psi:{\mathbb H}\rightrightarrows CB({\mathbb H})$ are single-valued and multivalued mappings, respectively. We signify the Problem (3.1) as GVIP and its solution set by $\Omega({\mathbb H}, M, \Phi, G, \eta)$.

Lemma 3.1. Let $\eta, \Phi:{\mathbb H}\times {\mathbb H} \to {\mathbb H}$ and $G, \psi, \varphi, f, g: {\mathbb H} \to {\mathbb H}$ be the single-valued mappings and $\Psi:{\mathbb H} \rightrightarrows CB({\mathbb H})$ a multivalued mapping. Let $M:{\mathbb H}\times{\mathbb H} \rightrightarrows {\mathbb H}$ be a generalized $\eta$-co-monotone mapping. Then, $(\theta, \omega)$, where $\theta\in {\mathbb H}, \omega\in\Psi(\theta)$ solves GVIP (3.1) if, and only if,

Proof. One can obtain the conclusion immediately by implementing (2.2). □

A mapping $F:{\mathbb H}\to {\mathbb H}$ is referred to as non-expansive (NM) if $\|F(\theta)-F(\vartheta)\|\leq\|\theta-\vartheta\|, \forall \theta, \vartheta\in {\mathbb H}$. In ^[19], the authors defined a generalized NM referred to as asymptotically nonexpansive (ANM) which properly includes the class of NM.

Definition 3.1. ^[19] A mapping $F:{\mathbb H}\to {\mathbb H}$ is known as ANM if $\exists$ is a sequence $\{\varepsilon_{n}\}\subseteq[1, \infty)$ with $\lim\limits_{n\to \infty}\varepsilon_{n} = 1$ and $\forall n\in\mathbb N$,

In an attempt to obtain extension of NM and ANM, Sahu ^[30] introduced nearly asymptotically non-expansive mapping (NANM). The class of NANM is an intermediate class which contains the class of ANM and is contained in the class of mappings of asymptotically non-expansive type.

Definition 3.2. A mapping $F:{\mathbb H}\to {\mathbb H}$ is known as NANM, if $\exists \{\varepsilon_{n}\}\subseteq[1, \infty)$ and $\{\upsilon_{n}\}\subseteq [0, \infty)$ with $\lim\limits_{n\to \infty}\varepsilon_{n} = 1, \lim\limits_{n\to \infty}\upsilon_{n} = 0$, $\forall n\in\mathbb N$,

Further, Alber et al. ^[8] made an attempt to unify some classes of generalized NMs by introducing total asymptotically non-expansive mapping (TANM).

Definition 3.3. A mapping $F:{\mathbb H}\to {\mathbb H}$ is known as TANM if $\exists$ nonnegative sequences of real numbers $\{\varepsilon_{n}\}, \{\upsilon_{n}\}$ with $\lim\limits_{n\to \infty}\varepsilon_{n} = 0 = \lim\limits_{n\to \infty}\upsilon_{n}$ and a strictly increasing continuous function $\gamma:{\mathbb R}^{+}\to {\mathbb R}^{+}$ such that $\gamma(0) = 0$ and $\forall n\in\mathbb N$,

Let $F:{\mathbb H}\to\mathbb H$ be a TANM and presume that the mappings $\eta, \Phi, G, \psi, \varphi, f, g, \Psi$, and $M$ are identical as in Lemma 3.1. Suppose that $\theta^{*}\in Fix(F)\cap \Omega({\mathbb H}, M, \Phi, G, \eta)$, then from (3.2), one can achieve the following formulation:

where $\varrho > 0$ and $\omega^{*}\in \Psi(\theta^{*})$. By the virtue of formulation (3.3), we design the following Ishikawa type resolvent iterative scheme to explore a common element of $Fix(F)$ and $\Omega({\mathbb H}, M, \Phi, G, \eta)$. Here, $Fix(F)$ indicates the set of fixed points of TANM $F$ and $\Omega({\mathbb H}, M, \Phi, G, \eta)$ indicates the solution set of GVIP (3.1).

Algorithm 3.1. Let $\eta, \Phi:{\mathbb H}\times {\mathbb H} \to {\mathbb H}$ and $G, \psi, \varphi, f, g: {\mathbb H} \to {\mathbb H}$ be the single-valued mappings. Let $\Psi:{\mathbb H} \rightrightarrows CB({\mathbb H})$ be a multivalued mapping; $M_{n}, M:{\mathbb H}\times{\mathbb H} \rightrightarrows {\mathbb H}$ be generalized $\eta$-co-monotone mappings, and $F:{\mathbb H}\to\mathbb H$ be a TANM. For initial points $\theta_{0}, \vartheta_{0}\in {\mathbb H}, \omega_{0}\in \Psi(\theta_{0})$, estimate the sequences $\{\theta_{n}\}, \{\omega_{n}\}$ by the following procedure:

for $n = 0, 1, 2, \cdots$, ${\omega}_{n}\in \Psi(\theta_{n}), \bar{\omega}_{n}\in \Psi(\vartheta_{n})$, $0\leq \alpha_{n}, \beta_{n}\leq 1, \sum\limits_{n = 0}^{\infty}\alpha_{n} = \infty$, and $\varrho > 0$.

Theorem 3.1. Let $\eta:{\mathbb H}\times {\mathbb H} \to {\mathbb H}$ be a $\pi$-Lipschitz continuous mapping; $\Phi:{\mathbb H}\times {\mathbb H} \to {\mathbb H}$ and $\psi, \varphi, f, g: {\mathbb H} \to {\mathbb H}$ be the single-valued mappings such that $\Phi(\cdot, \cdot)$ is $m$-mixed Lipschitz continuous with respect to $\psi$ and $\varphi$ and $\iota$-mixed strongly monotone with respect to $G$ and $\Psi$, $G$ is $t$-Lipschitz continuous, $\Psi$ is $\cal D$-Lipschitz continuous with constant $r$, $\psi$ is $\varsigma$-expansive, and $\varphi$ is $l$-Lipschitz continuous. Let $M_{n}, M:{\mathbb H}\times{\mathbb H} \rightrightarrows {\mathbb H}$ be generalized $\eta$-co-monotone mappings. Let $F:{\mathbb H}\to{\mathbb H}$ be a $(\{\mu_{n}\}, \{\nu_{n}\}, \phi)$-TANM so that $Fix(F)\cap \Omega({\mathbb H}, M, \Phi, G, \eta)\neq \emptyset$. If $\varrho > 0$ obeys the following relation:

(i) Then $\Omega({\mathbb H}, M, \Phi, G, \eta)$ is singleton.

(ii) If $M_{n}\underrightarrow{\mathbb G} M$, then the sequence $\{\theta_{n}\}$ induced by (3.4)-(3.5) converges strongly to $\theta\in Fix(F)\cap \Omega({\mathbb H}, M, \Phi, G, \eta)$.

Proof. $(i)$ Define ${\cal G}: {\mathbb H}\to {\mathbb H}$ as

By making use of Proposition 2.1 and (3.7), for all $\theta, \vartheta\in {\mathbb H}$, we acquire

Utilizing the $m$-mixed Lipschitz continuity and $\iota$-mixed strong monotonicity of $\Phi$ and Lipschitz continuities of $G$ and $\Psi$, we acquire

After simplification, the above inequality turns into

Thus, (3.10) and (3.8) yield

where $\Theta = \Xi\sqrt{m^{2}-2\varrho\iota+\varrho^{2}t^{2}r^{2}}$ and $\Xi = \frac{\pi}{[\varrho(\tau^{'}-\tau^{''})+(\kappa^{'}\varsigma^{2}-\kappa^{''}l^{2})]}$. Taking the premise (3.6) into consideration, we see that $0\leq \Theta < 1$. Thus, $\cal G$ being a contraction mapping owns a unique fixed point, i.e., $\exists$ a unique $\theta\in\mathbb H$ so that ${\mathbb R}^{\eta, \Phi(\cdot, \cdot)}_{\varrho, M(\cdot, \cdot)}[\Phi(\psi(\theta), \varphi(\theta))-\varrho G(\omega)] = \theta$. Consequently, Lemma 3.1 guarantees that $\Omega({\mathbb H}, M, \Phi, G, \eta)$ is singleton.

$(ii)$ By the assumption that $\emptyset\neq Fix(F)\cap \Omega({\mathbb H}, M, \Phi, G, \eta)$ and in $(i)$, we confirmed that $\Omega({\mathbb H}, M, \Phi, G, \eta)$ is singleton. Suppose that $\Omega({\mathbb H}, M, \Phi, G, \eta) = \{\theta\}$, then we deduce that $\theta\in Fix(F)$ and consequently, by (3.3), one can express

Utilizing the Proposition 2.1, we get

where $\Sigma_{n} = {\mathbb R}^{\eta, \Phi(\cdot, \cdot)}_{\varrho, M_{n}(\cdot, \cdot)}[\Phi(\psi(\theta), \varphi(\theta))-\varrho G(\omega)]-{\mathbb R}^{\eta, \Phi(\cdot, \cdot)}_{\varrho, M(\cdot, \cdot)}[\Phi(\psi(\theta), \varphi(\theta))-\varrho G(\omega)]$. Utilizing the Lipschtz continuities of $\Psi$ and $G$, we acquire

Also, utilizing $m$-mixed Lipschitz continuity of $\Phi$ regarding $\psi$ and $\varphi$, $\iota$-mixed strong monotonicity with respect to $G$ and $\Psi$ and combining (3.14), we acquire

which yields

After substituting (3.15) into (3.13), we obtain

where $\Theta = \Xi\sqrt{ m^{2}-2\varrho\iota+\varrho^{2}t^{2}r^{2}}$. Now, recalling that $F$ is $(\{\mu_{n}\}, \{\nu_{n}\}, \phi)$-total asymptotically non-expansive and applying (3.4) and (3.12), we get

By substituting (3.16) in (3.17), we acquire

Following the same steps and employing the same facts as in (3.17), it follows from (3.5) and (3.12) that

By the hypothesis $M_{n}\underrightarrow{\mathbb G}M$, we obtain $\Sigma_{n}\to 0$, thus from (3.18) and (3.19), we deduce that

Substituting (3.21) into (3.20), we acquire

where $\Psi_{n} = \Theta\|\theta_{n}-\theta\|$ and $\Gamma_{n} = [1-\beta_{n}(1-\Theta)]\|\theta_{n}-\theta\|$. For each $n\geq n_{0},$ setting $p_{n} = \|\theta_{n}-\theta\|, q_{n} = \alpha_{n}(1-\Theta)$ and $\tau_{n} = \frac{\beta_{n}\Theta[\mu_{n}\phi(\Psi_{n})+\nu_{n}]+\mu_{n}\phi[\Theta\{\Gamma_{n}+\mu_{n}\phi (\Psi_{n})+\nu_{n}\}]+\nu_{n}}{(1-\Theta)}$. Clearly, $\sum_{n = 0}^{\infty}q_{n} = \infty$ because of $\sum_{n = 0}^{\infty}\alpha_{n} = \infty$. In fact, $\mu_{n}, \nu_{n}\to 0$ as $n\to \infty$ yields $\tau_{n} = 0$. Thus, we deduce from Lemma 2.1 that $\lim\limits_{n\to \infty}p_{n} = 0$ and, hence, $\lim\limits_{n\to \infty}\theta_{n} = \theta$. □

Example 3.1. Let ${\mathbb H} = [0, \infty)$ with inner product $\langle \theta, \vartheta\rangle = \theta\vartheta$ and norm $|\cdot|$. Define $F(\theta) = \sin{\theta}, \forall \theta\in [0, \infty)$. Then, clearly $0\in Fix(F)$ for all $\theta, \vartheta\in [0, \infty)$, and we express

Thus, $F$ is non-expansive, hence $F$ is TANM with $\mu_{n} = \frac{1}{n^{2}}$ and $\nu_{n} = \frac{1}{n^{3}}, \forall n\geq 1$. Define the mappings $\eta, \Phi:{\mathbb H}\times {\mathbb H}\to{\mathbb H}$ and $G, \psi, \varphi, f, g:{\mathbb H}\to {\mathbb H}$ by

It can be easily observed that $\eta, G$, and $\varphi$ are Lipschitz continuous with constants $\pi = \frac{1}{4}, t = \frac{1}{2}$, and $\varphi = \frac{1}{4}$, respectively, and $\psi$ is $\frac{3}{4}$-expansive. Also,

i.e., $\Phi(\cdot, \cdot)$ is $1/2$-mixed Lipschitz continuous, $1/8$-mixed strongly monotone, and symmetric $\eta$-co-coercive with respect to $\psi$ and $\varphi$ with constants $1/3$ and $1$, respectively. Define $M:{\mathbb H}\times {\mathbb H}\rightrightarrows{\mathbb H}$ and $\Psi:{\mathbb H}\to CB(H)$ by $M(f(\theta), g(\theta)) = \frac{f(\theta)+g(\theta)}{3}\; \; {\rm and} \; \; \Psi(\theta) = \Big\{\frac{\theta}{5}+1\Big\}.$ Then, $\Psi$ is $1/5$-Lipschitz continuous and

i.e., $M(\cdot, \cdot)$ is symmetric $\eta$-monotone with respect to $f$ and $g$ with constants $1/3$ and $1/6$, respectively. Thus, $M(\cdot, \cdot)$ is a generalized $\eta$-co-monotone mapping. Also, ${\cal G}(\theta) = {\mathbb R}^{\eta, \Phi(\cdot, \cdot)}_{\varrho, M(\cdot, \cdot)}[\Phi(\psi(\theta), \varphi(\theta))-\varrho G(\omega)] = \frac{5}{2}\theta$ and the estimated constants satisfy (3.6), that is, $\sqrt{m^{2}-2\varrho\iota+\varrho^{2}t^{2}r^{2}} < \frac{[\varrho(\tau^{'}-\tau^{''})+(\kappa^{'}\varsigma^{2}-\kappa^{''}l^{2})]}{\pi}$. Therefore, $\theta^{*} = 0\in {\mathbb H}$ is a unique fixed point of $\cal G$. Thus, we have $\theta^{*} = 0\in Fix(F)\cap \Omega({\mathbb H}, M, \Phi, G, \eta)$. Next, we compute the sequence $\{\theta_{n}\}$ by employing Algorithm 3.1. Let $\alpha_{n} = \frac{n}{2n+1}$ and $\beta_{n} = \frac{1}{n+1}$. Then

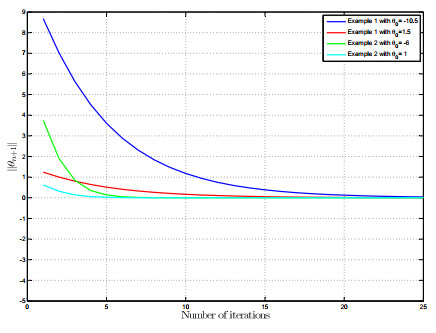
For different initial points: $\theta_{0} = -10.5$ and $\theta_{0} = 1.5$, the sequence $\theta_{n}\to 0$ and $0\in Fix(F)\cap \Omega({\mathbb H}, M, \Phi, G, \eta)$ and the convergence behavior of $\{\theta_{n}\}$ is shown in Figure 1.

Example 3.2. Let ${\mathbb H} = \mathbb R$ with inner product $\langle \theta, \vartheta\rangle = \theta\cdotp\vartheta$ and norm $|\cdot|$. Define $F(\theta) = \sin{\theta}, \forall \theta\in \mathbb R$. Then, clearly $F$ is TANM with $\mu_{n} = \frac{1}{n^{2}}$ and $\nu_{n} = \frac{1}{n^{3}}, \forall n\geq 1$ and $0\in Fix(F)$. Define the mappings $\eta, \Phi:{\mathbb H}\times {\mathbb H}\to{\mathbb H}$ and $G, \psi, \varphi, f, g:{\mathbb H}\to {\mathbb H}$ by

Then $\eta, G$, and $\varphi$ are Lipschitz continuous with constants $\pi = t = \frac{1}{3}$ and $l = \frac{1}{4}$, respectively, and $\psi$ is $\frac{1}{2}$-expansive. Also, $\Phi(\cdot, \cdot)$ is $1/8$-mixed Lipschitz continuous, $1/16$-mixed strongly monotone, and symmetric $\eta$-co-coercive with respect to $\psi$ and $\varphi$ with constants $1/3$ and $2/3$, respectively. Define $M:{\mathbb H}\times {\mathbb H}\rightrightarrows{\mathbb H}$ and $\Psi:{\mathbb H}\to CB(H)$ by $M(f(\theta), g(\theta)) = \frac{f(\theta)+g(\theta)}{3}\; \; {\rm and} \; \; \Psi(\theta) = \Big\{\theta\Big\}.$ Then, $\Psi$ is $1$-Lipschitz continuous and $M(\cdot, \cdot)$ is symmetric $\eta$-monotone with respect to $f$ and $g$ with constants $2/9$ and $1/9$, respectively. Thus, $M(\cdot, \cdot)$ is a generalized $\eta$-co-monotone mapping. Also, for $\varrho = 1$, the estimated constants satisfy (3.6), that is, $\sqrt{m^{2}-2\varrho\iota+\varrho^{2}t^{2}r^{2}} < \frac{[\varrho(\tau^{'}-\tau^{''})+(\kappa^{'}\varsigma^{2}-\kappa^{''}l^{2})]}{\pi}$ and ${\mathbb R}^{\eta, \Phi(\cdot, \cdot)}_{\varrho, M(\cdot, \cdot)}[\Phi(\psi(\theta), \varphi(\theta))-\varrho G(\omega)] = -\frac{5}{11}\theta.$ Therefore, $0\in {\mathbb R}$ is a unique fixed point of ${\mathbb R}^{\eta, \Phi(\cdot, \cdot)}_{\varrho, M(\cdot, \cdot)}[\Phi(\psi(\theta), \varphi(\theta))-\varrho G(\omega)]$. Thus, we have $0\in Fix(F)\cap \Omega({\mathbb H}, M, \Phi, G, \eta)$. Now for $\alpha_{n} = \frac{n}{2n+1}$ and $\beta_{n} = \frac{1}{n+1}$, we compute the sequence $\{\theta_{n}\}$ by employing Algorithm 3.1 as under:

For different initial points: $\theta_{0} = 6,$ and $\theta_{0} = 1$, the sequence $\theta_{n}\to 0$ and $0\in Fix(F)\cap \Omega({\mathbb H}, M, \Phi, G, \eta)$ and the convergence is shown by the graph (Figure 1) below.

4.   Generalized resolvent dynamical system

Herein, we employ the technique of the dynamical system to explore the solution of GVIP (3.1). By utilizing Lemma 3.1, the generalized resolvent dynamical system (GRDS) that we examine is as under:

where $\theta\in {\mathbb H}, \omega\in \Psi(\theta)$, and $\xi > 0$ is a parameter.

Definition 4.1. ^[24] It is stated that the GRDS (4.1) converges to the solution set $\Omega({\mathbb H}, M, \Phi, G, \eta)$ of GVIP (3.1) if the trajectory of the dynamical system, irrespective of the initial point, satisfies

where

If $\theta^{*}$ is a unique point of $\Omega$, then $\lim\limits_{t\to\infty}\theta(s) = \theta^{*}.$

Definition 4.2. ^[25] The dynamical system is referred to as globally exponentially stable with degree $k$ at $\theta^{*}$ if the trajectory of the dynamical system, irrespective of the initial point, satisfies

where positive constants $k$ and $c_{0}$ do not depend on the initial point.

Lemma 4.1. ^[26] Let $\tilde{\theta}$ and $\tilde{\vartheta}$ be real-valued nonnegative continuous functions with domain $\{s:s\geq s_{0}\}$ and let $\alpha(s) = \alpha_{0}(|s-s_{0}|)$ where $\alpha_{0}$ is a monotonic increasing function. If for all $s\geq s_{0}$,

then

Next, by utilizing Lemma 4.1 and Theorem 3.1, we investigate the unique solution of GRDS (4.1).

Theorem 4.1. Assume that the Theorem 3.1 holds. Then, for each $\theta_{0}\in {\mathbb H}$ with $\omega_{0}\in \Psi(\theta_{0})$, there exists a unique continuous solution $\theta(s)$ with $\theta(s_{0}) = \theta_{0}$ of GRDS (4.1) over $[s_{0}, \infty)$.

Proof. Define

Invoking the arguments as for (3.8), we obtain

Invoking the arguments as employed to (3.9), we obtain

(4.2) and (4.3) together yields

which proves that ${\cal G}$ is locally Lipschitz continuous in $\mathbb H$. Thus, for each $\theta_{0}\in \mathbb H, \exists$ a unique continuous solution $\theta(s)$ of GRDS (4.1) with $\theta(s_{0}) = \theta_{0}$ in the interval $s_{0}\leq s < {\cal S}$. Let the maximal interval of its existence be $[s_{0}, {\cal S})$. Next, we substantiate that ${\cal S} = \infty$. Now, for any $\theta\in {\mathbb H}, \omega\in\Psi(\theta)$, we have

Employing the integral on (4.5) over $[s_{0}, s]$ and utilizing Lemma 4.1, we get

where $k_{5} = \xi(1+\Theta)\|\theta^{*}\|$ and $k_{6} = \xi(1+\Theta)$. Hence the solution is bounded on $[s_{0}, {\cal S})$, so ${\cal S} = \infty.$ □

In the next theorem, we shall examine GVIP (3.1) by the convergence of the trajectory of the solution of considered GRDS (4.1).

Theorem 4.2. Assume Theorem 3.1 is true. Then, GRDS (4.1) converges globally exponentially to the unique solution $\theta^{*}\in \Omega({\mathbb H}, M, \Phi, G, \eta)$.

Proof. It is evident from the Theorem 4.1 that GRDS (4.1) owns a unique solution. Assume that $\theta(s) = (s, s_{0};\theta_{0})$ is a solution of GRDS (4.1) with $\theta(s_{0}) = \theta_{0}$. Define the Lyapunov function $\cal L$ on $\mathbb H$ by

We obtained the relation $\theta = {\mathbb R}^{\eta, \Phi(\cdot, \cdot)}_{\varrho, M(\cdot, \cdot)}[\Phi(\psi(\theta), \varphi(\theta))-\varrho G(\omega)]$ from the Lemma 3.1 and, utilizing (3.8)–(3.11), we acquire

which yields

where $\Theta = \Xi\sqrt{ m^{2}-2\varrho\iota+\varrho^{2}t^{2}r^{2}}$ and $\Xi = \frac{\pi}{[\varrho(\tau^{'}-\tau^{''})+(\kappa^{'}\varsigma^{2}-\kappa^{''}l^{2})]}$. Thus, we acquire

From (3.6), we know that $1-\Theta > 0$. As a result, the trajectory of the solution of GRDS (4.1) converges globally exponentially to the unique solution of GVIP (3.1). □

5.   Conclusions

In this work, we investigate a generalized variation inclusion problem. The resolvent operator for generalized $\eta$-co-monotone mapping is structured, the Lipschitz constant is estimated and its relationship with the graph convergence is accomplished. An Ishikawa type iterative algorithm is designed and employed to explore the common solution of the generalized variational inclusion and the set of fixed points of a TANM by using the novel implication of graph convergence. Moreover, a generalized resolvent dynamical system is considered and implemented to examine the considered generalized variation inclusion problem.

Author contributions

DF: funding, writing review and editing, supervision; MD: conceptualization, writing review and editing; MA: conceptualization, writing original draft preparation, writing review and editing, supervision. All authors have read and approved the final version of the manuscript for publication.

Use of AI tools declaration

The authors declare they have not used AI tools in the creation of this article.

Acknowledgments

The first author acknowledges the Princess Nourah bint Abdulrahman University Researchers Supporting Project, project number PNURSP2024R174, Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Conflict of interest

Authors declare no conflicts of interest in this paper.