Green closed-loop supply chain optimization strategy considering CER and incentive-compatibility theory under uncertainty

Jianquan Guo; Guanlan Wang; Mitsuo Gen; Jianquan Guo; Guanlan Wang; Mitsuo Gen

doi:10.3934/mbe.2022443

Mathematical Biosciences and Engineering

2022, Volume 19, Issue 9: 9520-9549. doi: 10.3934/mbe.2022443

Previous Article Next Article

Research article Special Issues

Green closed-loop supply chain optimization strategy considering CER and incentive-compatibility theory under uncertainty

1.
Sino-German College, University of Shanghai for Science and Technology, Shanghai, China
2.
Business School, University of Shanghai for Science and Technology, Shanghai, China
3.
Fuzzy Logic Systems Institute/Tokyo University of Science, Japan

Received: 08 April 2022 Revised: 17 June 2022 Accepted: 26 June 2022 Published: 30 June 2022

Under the uncertain market demand and quality level, a total profit model of green closed-loop supply chain system (GCL-SCS) considering corporate environmental responsibility (CER) and government differential weight subsidy (GDWS) is constructed. Based on incentive-compatibility theory, the optimal subsidy allocation policy and green investment level were explored. Fuzzy chance-constrained programming (FCCP) is used to clarify the uncertainty factors of this model; while genetic algorithm (GA) and CPLEX are used to find and compare a calculating example's approximate optimal solution about this model. The main calculating results indicate that: (1) Enterprises can make optimal recycling, production and sales strategies according to different potential demand; (2) Without government subsidy, enterprises' higher green investment level will reduce their average gross profit, increase the quality level of recycled products and decrease the recycling rate, hence reduce their environmental protection willingness; (3) Based on incentive-compatibility theory, when government subsidy weight is set as 0.34~0.41 for consumers, enterprises' higher green investment level will enhance their average gross profit, reduce the quality level of recycled products and increase the recycling rate, which will improve their environmental protection willingness; (4) Under uncertain environment, the combination of reasonable government subsidy policy and enterprises green investment can make up for the defect of enterprises green investment alone, maximize utilities of government and enterprises, and optimize the green closed loop supply chain.

Keywords:

Citation: Jianquan Guo, Guanlan Wang, Mitsuo Gen. Green closed-loop supply chain optimization strategy considering CER and incentive-compatibility theory under uncertainty[J]. Mathematical Biosciences and Engineering, 2022, 19(9): 9520-9549. doi: 10.3934/mbe.2022443

Related Papers:

[1]	Zheng Liu, Lingling Lang, Lingling Li, Yuanjun Zhao, Lihua Shi . Evolutionary game analysis on the recycling strategy of household medical device enterprises under government dynamic rewards and punishments. Mathematical Biosciences and Engineering, 2021, 18(5): 6434-6451. doi: 10.3934/mbe.2021320
[2]	Rui Huang, Hao Xiao, Guoqin Pan . Authority decentralization and air pollution reduction: Evidence from China. Mathematical Biosciences and Engineering, 2022, 19(12): 14212-14231. doi: 10.3934/mbe.2022661
[3]	César Augusto Henao, Ana Batista, Andrés Felipe Porto, Virginia I. González . Multiskilled personnel assignment problem under uncertain demand: A benchmarking analysis. Mathematical Biosciences and Engineering, 2022, 19(5): 4946-4975. doi: 10.3934/mbe.2022232
[4]	Bowen Ding, Zhaobin Ma, Shuoyan Ren, Yi Gu, Pengjiang Qian, Xin Zhang . A genetic algorithm with two-step rank-based encoding for closed-loop supply chain network design. Mathematical Biosciences and Engineering, 2022, 19(6): 5925-5956. doi: 10.3934/mbe.2022277
[5]	Shan Huang, Khor Teik Huat, Yue Liu . Study on the influence of Chinese traditional culture on corporate environmental responsibility. Mathematical Biosciences and Engineering, 2023, 20(8): 14281-14305. doi: 10.3934/mbe.2023639
[6]	Pengpeng Wang, Xu Wang, Yumin Shen, Jinlong Wang, Xiaoyun Xiong . PBFT optimization algorithm based on community contributions. Mathematical Biosciences and Engineering, 2023, 20(6): 10200-10222. doi: 10.3934/mbe.2023447
[7]	Sheng-I Chen, Chia-Yuan Wu . A stochastic programming model of vaccine preparation and administration for seasonal influenza interventions. Mathematical Biosciences and Engineering, 2020, 17(4): 2984-2997. doi: 10.3934/mbe.2020169
[8]	Yukun Song, Yue Song, Yongjun Wu . Adaptive boundary control of an axially moving system with large acceleration/deceleration under the input saturation. Mathematical Biosciences and Engineering, 2023, 20(10): 18230-18247. doi: 10.3934/mbe.2023810
[9]	Song Liu, Gusong Luo, Yonglong Cai, Wenjie Wu, Weitao Liu, Rong Zou, Wenxuan Tan . Determinants of consumer intention to adopt a self-service technology strategy for last-mile delivery in Guangzhou, China. Mathematical Biosciences and Engineering, 2024, 21(2): 3262-3280. doi: 10.3934/mbe.2024144
[10]	Yue Liu, Liming Chen, Han Luo, Yuzhao Liu, Yixian Wen . The impact of intellectual property rights protection on green innovation: A quasi-natural experiment based on the pilot policy of the Chinese intellectual property court. Mathematical Biosciences and Engineering, 2024, 21(2): 2587-2607. doi: 10.3934/mbe.2024114

Abstract

1. Introduction

With the shortage of natural resources and the continuous deterioration of ecological environment, circular economy has attracted more and more attention from all walks of life ^[1]. As an important part of the closed-loop supply chain system in the circular economy, recycling and remanufacturing activities can not only realize the efficient utilization of resources, but also reduce the adverse effects of waste pollution and over exploitation of resources ^[2]. Moreover, remanufacturing production, if properly handled, can decrease production cost, enhance productivity efficiency, and effectively improve the competitive advantage of enterprises ^[3]. However, closed loop supply chain management is more complex and there are still many challenges, for instance, how could enterprises make optimal decisions under uncertain environment and how could government formulates reasonable subsidy allocation policy to enhance enterprises' green investment level and the implementation effect of recycling and remanufacturing ^[4].

Major uncertainty factors such as market demand, recovery quality, recycling rate, green level of recycled products, and buyback and remanufacturing costs, make green closed loop supply chain management more sophisticated and add more difficulties for enterprises to make recycling, production, and sales decisions ^[5]. Disturbances in market demand greatly affect production operation ^[6]. Uncertain recovery quality simultaneously affects recycling rate, buyback and remanufacturing costs, and green level of recycled products ^[7]. Therefore, demand and recovery quality are more important uncertainty factors. Wang et al. ^[8] regarded uncertain demand and manufacturing cost as fuzzy variables and analyzed optimal pricing policies considering green investment and sales effort. Li et al. ^[9] took random demand into consideration and established a theoretical model in which the remanufacturer plays as a leader and the recycler acts as a follower. Dai et al. ^[10] considered a dual-channel supply chain composed of a manufacturer and a retailer in which each member obtains heterogeneous forecasting information about uncertain demand. Zhu et al. ^[11] optimized decisions for hierarchical industrial status of the SME, CE and CB under the uncertainties of market demand. Zeballos et al. ^[12] proposed a scenario-based stochastic mixed-integer programming model considering uncertain recovery quality. Jeihoonian et al. ^[13] designed a closed-loop supply chain network under uncertain quality status with a case of durable products. Heydari et al. ^[14] investigated a two-echelon reverse supply chain considering uncertain recovered quality that follows a uniform distribution. The above studies separately analyzed uncertain market demand or recovery quality. However, in reality, market demand is often divided into new products demand and remanufactured products demand ^[15], moreover, for enterprises, the proportion of new products and remanufactured products is related to the quality of recycled products. Based on above analysis, this paper simultaneously discusses uncertain market demand (new products and remanufactured products demand) and recovery quality.

Stochastic programming, robust optimization, and fuzzy chance constrained programming are currently used methods to solve the uncertainty problem in closed-loop supply chain. Ghelichi et al. ^[16] established a two-stage stochastic programming model for the design of an integrated green biodiesel supply chain network from Jatropha Curcas feedstocks, and a flexible stochastic programming approach was developed and applied to the supply chain network model. Farrokh et al. ^[17] used robust optimization to solve the problem of uncertain demand and studied the impact of uncertain demand on net profit. Ahmadi et al. ^[18] established a multi-objective mixed integer linear programming model considering uncertain requirements and adopted the fuzzy chance constraint programming method to solve uncertain problems. Josefa et al. ^[19] compared stochastic programming with fuzzy chance-constrained programming to solve the problem of uncertain demand and concluded that fuzzy chance-constrained programming is easier to obtain the optimal solution. Lima et al. ^[20] used a fuzzy programming approach to design and plan the downstream oil supply chain under uncertainty. Ziya-Gorabi et al. ^[21] used fuzzy chance constrained programming to solve and optimize the problem of a mixed-integer linear programming (MILP) model with three objectives in both definite and indefinite states. By comparing the three methods, it can be found that stochastic programming can solve uncertain problems relatively accurately, but it requires enough statistical data and is too complicated to solve multi-scene problems ^[19]. Robust optimization can effectively deal with the changes of fuzzy parameters, but too much emphasis on confidence level will lead to conservative results ^[22]. Relatively speaking, fuzzy chance constraint programming can not only solve the problem of lack of accurate values, but also constrain confidence level according to the attitude of decision-makers, and avoid overly conservative results, thus making the model flexible, and more in line with the actual situation of enterprise decision-making ^[23]. In this paper, fuzzy chance-constrained programming is thus used to solve the demand uncertainty problem of both new products and remanufactured products.

The purpose of building a green supply chain is to pursue both economic benefits and green benefits, that is, environmental benefits, so as to achieve the sustainable development of society. At present, enterprises pay attention not only to their competitiveness but also to their social image ^[24]. In recent years, many scholars have conducted extensive research on consumers' green preference behavior. Jian et al. ^[25] designed a green closed-loop supply chain with profit sharing contract coordination fairness. Liu et al. ^[26] optimized the network's worst-case performance based on a trade-off between upside risk and economic cost expectations in a green closed-loop supply chain. Asghari et al. ^[27] examined a single-stage green closed-loop supply chain (GCLSC) in which the green manufacturer, retailer, and collector try to reform the environmental effects of their operations, products, and services across the value chain according to their environmental responsibilities. The above research only involve the study of green preference behavior, but this paper intends to take greenness as a parameter to specifically study the relationship between total profit, weighted subsidy and greenness level.

Corporate Environmental Responsibility (CER) can not only enhance economic benefits and improve corporate image, but has a practical significance for environmental protection ^[28]. Moreover, consumers' preference for environmentally friendly products can bring unique competitive advantages for enterprises ^[29]. Marchi et al. ^[30] found that CER played a strategic role in closed loop supply chain management. Huang et al. ^[31] explored the impact of carbon policy and environmental responsibility investment on the integrated inventory. Hong et al. ^[32] considered stakeholders' environmental responsibilities in a two-echelon supply chain in which a manufacturer designed and produced green products. Cheng et al. ^[33] established six game models considering environmental protection responsibility in order to address the optimal power structure problem. Han et al. ^[34] constructed an environmental responsibility improved input-output measurement model of corporate energy consumption and pollution discharge in industrial parks. Yang et al. ^[35] employed game models of a sustainable supply chain, considering environmental responsibilities under different channel leaderships. The above studies discussed the impact of corporate environmental responsibility on the optimal decision in a single cycle closed loop supply chain production. However, in real production activities, manufacturing and remanufacturing production is often carried out in multiple cycles ^[36]. Therefore, this paper studied CER through green investment in the multi-cycle closed loop supply chain.

Government subsidies play an important role in encouraging enterprises to make green investment and improving the implementation effect of recycling and remanufacturing ^[37]. Zheng et al. ^[38] discussed the impact of government subsidies on technological improvement and market demand and concluded that government's subsidies to manufacturers are beneficial to reduce technological improvement costs and expand green product market. Chen et al. ^[39] established an evolutionary game theory model based on carbon tax and subsidy, and studied the optimal decision of manufacturers under four different combinations of carbon tax and subsidy. Cohen et al. ^[40] studied the effect of subsidized consumers on production and pricing decisions in the context of demand uncertainty. Bian et al. ^[41] conducted a comparative study on the impact of subsidies to consumers and manufacturers on carbon emission reduction and social welfare. Deng et al. ^[42] studied the problem of optimal government-to-patient subsidy differential (G2P-SD) policy design. Wang et al. ^[43] analyzed the low-carbon decision of the construction supply chain under government subsidies with the help of differential game theory. Chen et al. ^[44] investigated the optimal production and subsidy rate of the supply chain considering consumer environmental awareness. In the above literature, subsidies to manufacturers and consumers were discussed separately, the unit total subsidy is fixed, and also the influence of recycled product quality level on the subsidies is not considered. This paper studies the influence of the government's differential weight subsidies to manufacturers and consumers on the optimal decision-making of closed-loop supply chain, moreover, the government will consider the quality level of recycled products in the process of giving subsidies.

Incentive-compatibility theory makes both enterprises and government tend to maximize utility through incentive strategies ^[45]. Reasonable incentive mechanism formulated by government can effectively expand green product market, and increase recycling rate and economic benefits while guide enterprises to make a higher green investment level ^[46]. Wang et al. ^[47] investigated a couple of incentive mechanisms for collaboratively enhancing product greenness and found that the proposed incentive mechanisms can contribute to improve overall utility. Qu et al. ^[48] studied the incentive problems associated with inventory investment and found that incentive distortion arised when retailers had to allocate inventory over time. Wang et al. ^[49] regarded government subsidy as incentive mechanism and concluded that subsidy incentive could affect the synergetic development. Zhang et al. ^[50] found that only the tariffs incentive set by government and the values of environmental impact satisfied a three-dimensional area, can two competitive firms ensure a stable market. Guo et al. ^[51] examines notions of incentive-compatibility in an environment with ambiguity-averse agents. Barberà et al. ^[52] proved that incentive-compatibility extends to groups, and that strategy-proofness implies strong group strategy-proofness in the special case of private values. Based on incentive-compatibility theory, this paper studies optimal subsidy allocation policy when both government and manufacturer tend to maximize utility considering government differential weighting subsidy for manufacturer and consumers purchasing remanufactured products.

Exact algorithm and meta-heuristic algorithm are often used to solve non-linear optimization issues with mixed integer variables. Among them, the exact algorithm can find the most accurate solution. In this paper, a classical accurate solution software, CPLEX is used to find the accurate solution of a calculating example of the model. Meta-heuristic algorithms are widely used to solve function optimization and discrete problems, such as monarch butterfly optimization (MBO), slime mould algorithm (SMA), moth search algorithm (MSA), hunger games search (HGS), Runge Kutta method (RKM), colony predation algorithm (CPA), Harris hawks optimization (HHO), and Genetic algorithm (GA). Feng et al. ^[53] found that MBO can outperform many state-of-the-art optimization techniques when solving global numerical optimization and engineering problems. In order to demonstrate the superior performance of the MBO algorithm, Wang et al. ^[54] carried out a comparative study with five other meta-heuristic algorithms through thirty-eight benchmark problems, and found that the MBO method is able to find the better function values on most benchmark problems as compared to five other meta-heuristic algorithms. Rahman et al. ^[55] used moth search algorithm (MSA) to optimize and validate the trade-off between the total cost of tardiness and batch delivery. Chouar et al. ^[56] investigated slime mould algorithm (SMA) to reduce cost in a PI-SCN hybrid framework based on an artificial neural network. Yang et al. ^[57] believed main feature of hunger games search is its dynamic nature, simple structure, and high performance in terms of convergence and acceptable quality of solutions. Nguyen et al. ^[58] introduced a novel and robust hybrid model for predicting BIGV based on the Hunger Games Search optimization algorithm (HGS) and ANN. Ambrosio et al. ^[59] provided a nonlinear stability analysis for a class of stochastic Runge-Kutta methods (RKM), applied to problems generating mean-square contractive solutions. Shi et al. ^[60] created an efficient intelligence method for the diagnosis of COVID-19 from the perspective of biochemical indexes, which is called the colony predation algorithm (CPA). Mashaleh et al. ^[61] presented a novel spam classification on email spam technique, which integrated the Harris Hawks optimizer (HHO) algorithm. The above research involve new algorithms in recent years, we can find the better function values on most benchmark problems as compared to other meta-heuristic algorithms. However, they are rarely used in closed-loop supply chain models at present.

Genetic algorithm (GA), as a heuristic random intelligent optimization algorithm to find the optimal solution through iteration, can process multiple individuals in the population at the same time, thus reducing the risk of falling into the local optimal solution. As a classical intelligent optimization algorithm, GA is widely used in function optimization and path optimization in the field of closed-loop supply chain ^[62]. Aiming at the carbon emission of e-commerce companies, Liu et al. ^[63] proposed GA to solve the joint design model of multi-cycle reverse logistics network. Sahebjamnia et al. ^[64] developed hybrid meta-heuristic algorithms, such as GA, Simulated Annealing (SA) and so on to improve the solution quality and decrease the computational time for solving the sustainable closed-loop tire supply chain network. Feng et al. ^[65] optimized BP neural network based on GA and PSO. Zhao et al. ^[66] carried out GA to validate the feasibility and applicability of emergency distribution route optimization for EV mobile power supply.

Considering that the main contribution of this paper is to establish a profit models of green closed loop supply chain system, the validity of the model is verified by numerical examples. In the past few years, GA has proved its good applicability and many papers also use GA as a reliable calculating method, by comparing the calculation results of CPLEX and GA in the small-scale case, the effectiveness of GA algorithm is verified in this paper.

Based on above analysis, this paper studies enterprises' optimal recovery, production and sales decisions under uncertain environments; and fatherly, based on incentive-compatibility, government's optimal subsidy allocation policy and enterprises' green investment level are also analyzed when both government and enterprises tend to maximize their utilities. This study could help enterprises make optimal decisions when faced with uncertain market demand and recovery quality, and also provide quantifiable suggestions for government to formulate reasonable subsidy allocation weight so as to effectively promote enterprises' enthusiasm for green investment and encourage enterprises to engage in recycling and remanufacturing. The comparison between the above literature and this study is shown in Table 1.

Table 1. Feature comparison of some relevant studies.

	Green Closed-loop supply chain	Incentive-compatibility	Uncertain demand	Uncertain recycling quality	GDWS	CER
Dominguez et al. (2019)				√
Atabaki et al. (2020)				√
Liao et al. (2020)				√
Khorshidvand et al. (2021)				√
Cohen et al. (2016)			√	√
Jeihoonian et al. (2017)				√
Li et al. (2019)			√	√
Almaraj et al. (2019)				√
Zhu et al. (2020)			√	√
Aminipour et al. (2021)			√
Dai et al.(2022)			√
Zhu et al. (2022)			√
Deng et al. (2021)			√		√
Wang et al. (2022)			√		√
Wang et al. (2020)			√		√
Chen et al. (2022)				√	√
Zheng et al. (2022)	√			√
Jian et al. (2021)	√			√
Liu et al. (2021)	√
Asghari et al. (2022)	√
Zhang et al. (2017)		√
Qu et al. (2018)		√
Suliman et al. (2019)		√
Nielsen et al. (2019)		√
Wang et al, 2020		√
Wang et al, 2021		√
Huiyi Guo et al.(2022)		√
Barberà et al. (2022)		√
Cheng et al, 2017			√			√
Marchi et al, 2018			√			√
Hong et al, 2019			√			√
Heydari et al, 2020			√			√
Huang et al, 2020			√			√
Wu et al, 2020			√			√
Feng et al, 2021			√			√
Yang et al, 2022			√			√
Han, & Cao, 2021			√			√
This article	√	√	√	√	√	√

| Show Table

DownLoad: CSV

The uniqueness and contributions of this paper are listed below:

(1) Incentive-compatibility theory is proposed to construct a green closed-loop supply chain model.

(2) The proposed green closed-loop supply chain model can solve the problem of optimal operation of remanufacturing enterprises under uncertain environments of market demands and quality level of recycled products.

(3) Two profit models of green closed loop supply chain system are constructed under no government subsidy and government differential weight subsidy considering CER.

(4) Quantified subsidy for government and green investment level for enterprises are provided.

The remainder of this paper is organized as follows: problem deﬁnitions, assumptions, and notations are stated in Section 2. Section 3 provides a derivation of the established models. Section 4 introduces solution techniques GA and CPLEX. The computational results, sensitivity analysis and managerial insights are rendered in Section 5. Finally, key conclusions of this study and potential future extensions are rendered in Section 6.

2. Problem deﬁnitions, notations, and assumptions

2.1. Problem deﬁnitions

Two gross profit models of green closed loop supply chain system were constructed under no government subsidy and government differential weight subsidy considering CER and incentive-compatibility respectively. This paper mainly deals with the following questions:

(1) How do uncertain demands of new products and remanufactured products affect manufacturers' optimal recycling, production, and sales decisions in the green closed loop supply chain?

(2) In the case of considering CER alone without government subsidy, how can green investment level affect gross profit, recycled products greenness, recycling rate, and manufacturer's enthusiasm for green investment?

(3) In the case of considering CER and government differential weighting subsidy, based on incentive-compatibility theory, how can government set a reasonable subsidy allocation weight to effectively incent manufacturer to set a higher green investment level, so as to achieve the effect of incentive-compatibility and the purpose of environmental protection?

2.2. Notations

To model the green closed loop supply chain system (GCL-SCS), the following notations are introduced.

2.2.1. Input parameters

Input parameters	Definition
$\sigma$	Recycled product greenness coefficient;
$w$	Subsidy weight for consumers, $0 < w < 1$ ;
${\alpha }_{n}$	Potential demand for new products per unit time;
${\alpha }_{r}$	Potential demand for remanufacturing products per unit time;
${\tau }_{1}$	Price sensitivity coefficient;
${\tau }_{2}$	Cross price sensitivity coefficient;
$\mu$	Sensitivity coefficient of demand to subsidy;
$l$	Sensitivity coefficient of demand to recycled products greenness;
$b$	Parameter of recycling rate function,   $0\le b\le 1$ ;
$\varphi$	Parameter of recycling rate function;
$a$	Parameter of buyback cost function, $0\le a\le 1$ ;
$\theta$	Parameter of buyback cost function;
c	Parameter of remanufacturing cost function, $0\le c\le 1$ ;
$\delta$	Parameter of remanufacturing cost function;
$e$	Green investment level;
$\pi$	Green investment cost parameter;
${q}_{s}$	Standard quality level of recycled products;
$t$	Adjustment factor of subsidy coefficient, $0\le t\le 1$ ;
$1/\beta$	Manufacturing rate, [unit]/[time], 0 < β < 1;
$1/\gamma$	Remanufacturing rate, [unit]/[time], 0 < γ < 1;
${h}_{s}$	Holding cost per unit time of serviceable stock;
${h}_{r}$	Holding cost per unit time of recycled products stock;
${h}_{raw}$	Holding cost per unit time of raw material stock;
${C}_{0}$	Ordering cost;
${C}_{\mathrm{n}}$	Manufacturing cost per unit;
${C}_{\mathrm{r}\mathrm{a}\mathrm{w}}$	Purchasing cost for raw material per unit;
${S}_{1}$	Manufacturing installation cost;
${S}_{2}$	Remanufacturing installation cost;
${d}_{n}$	Triangular fuzzy number of potential demand for new products;
${d}_{r}$	Triangular fuzzy number of potential demand for remanufacturing products;
$j$	Confidence level of potential demand for new products;
$k$	Confidence level of potential demand for remanufacturing products.

2.2.2. Output parameters

Output parameters	Definition
${D}_{n}$	Demand for new products per unit time;
${D}_{r}$	Demand for remanufacturing products per unit time;
$D$	Overall demand per unit time;
${V}_{1}$	Average setup cost for manufacturing;
${V}_{2}$	Average ordering cost;
${V}_{3}$	Average raw material holding cost;
${V}_{4}$	Average manufacturing cost;
${V}_{5}$	Inventory costs of raw materials and new products per unit time;
$d$	Recycling rate;
$p$	Buyback cost ratio;
$s$	Remanufacturing cost ratio;
$r$	Subsidy for unit remanufacturing product;
${S}_{m}$	Total subsidy for manufacturer;
${S}_{c}$	Total subsidy for consumers who buy remanufacturing products;
${T}_{m}$	Time interval of one remanufacturing lot;
${T}_{n}$	Time interval of one manufacturing lot;
${I}_{M}$	The maximum new products inventory;
${I}_{R}$	The maximum remanufacturing products inventory;
${I}_{r}$	The maximum recycled products inventory;
${I}_{raw}$	The maximum raw material inventory;
${H}_{M}$	Inventory carrying cost of remanufacturing products per unit time;
${H}_{R}$	Inventory carrying cost for new products per unit time;
${H}_{r}$	Inventory carrying cost of recycled products per unit time;
${H}_{raw}$	Inventory carrying cost of raw material per unit time;
${V}_{6}$	Average setup cost for remanufacturing;
${V}_{7}$	Average buyback cost;
${V}_{8}$	Average remanufacturing cost;
${V}_{9}$	Inventory costs of recycled products and remanufacturing products;
${V}_{10}$	Average green investment cost;
$AP$	Average gross profit under no government subsidy;
$APG$	Average gross profit under government differential weight subsidy.

2.2.3. Decision variables

Decision variables	Definition
$T$	Length of one manufacturing and remanufacturing cycle;
$m$	Number of remanufacturing lots, positive integer;
$n$	Number of manufacturing lots, positive integer;
$q$	The required minimum quality level of recycled products, $0\le q\le 1$ ;
$g$	Recycled product greenness;
${p}_{\mathrm{n}}$	Sales price of new products per unit;
${p}_{\mathrm{r}}$	Sales price of remanufacturing products per unit.

2.3. Assumptions

To model the green closed loop supply chain system, the following assumptions are introduced.

(1) The quality level of returned used products obeys standard normal distribution ^[67].

(2) Raw materials are purchased only once in a cycle ^[68].

(3) All recycled products are remanufactured ^[69], because there is a minimum quality level required for product recycling ^[70].

(4) Take no account of lead time, out of stock or surplus ^[68].

(5) Recycled products greenness is proportional to the recovery quality level: $g = \sigma q$ ^[71].

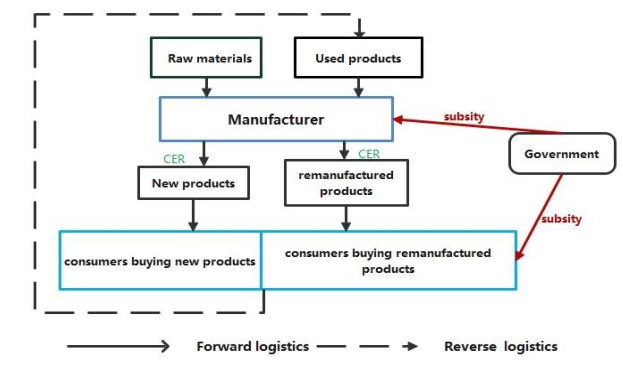
(6) Government subsidies manufacturers and consumers buying remanufacturing products with different allocation weights ^[72].The allocation weight for consumers is $w$ , and the corresponding allocation weight for manufacturer is $1-w$ .

(7) Market demand for new products is ${D}_{n} = {\alpha }_{n}-{\tau }_{1}{p}_{n}+{\tau }_{2}{p}_{r}-\mu \sqrt{wr}+l\sqrt{e}$ , market demand for remanufacturing products is ${D}_{r} = {\alpha }_{r}-{\tau }_{1}{p}_{r}+{\tau }_{2}{p}_{n}+\mu \sqrt{wr}+l\sqrt{e}$ , so the overall market demand is $D = {\alpha }_{n}+{\alpha }_{r}+\left({\tau }_{2}-{\tau }_{1}\right)\left({p}_{n}+{p}_{r}\right)+2l\sqrt{e}$ ^[73,74].

3. Mathematical modeling

As can be seen in Figure 1, the green closed loop supply chain system consists of the following parts: (1) Manufacturer purchases raw materials for new products production and recycles used products from consumers for remanufacturing activities. (2) Manufacturer undertakes CER by adopting green technology investment for new products and remanufactured products. (3) Consumers buy new products or remanufactured products and recycle used products to manufacturer. (4) Government subsidies manufacturer and consumers buying remanufactured products aiming to enhance the green investment level and implementation effect of recycling and remanufacturing. The whole process forms a material cycle flow.

Figure 1. Green closed loop supply chain system (GCL-SCS) model.

DownLoad: Full-Size Img PowerPoint

3.1. Cost of new products

3.1.1. Setup cost for manufacturing

At each cycle length T, manufacturing incurs a one-time production setup cost per unit time and it is given by:

${\mathrm{V}}_{1} = n{S}_{1}/T$

(1)

${V}_{1}$ represents average setup cost for manufacturing.

3.1.2. Ordering cost

Order cost is the cost incurred to replenish stocks. Its function is given by:

${V}_{2} = {C}_{0}/T$

(2)

${V}_{2}$ represents average ordering cost, and total ordering cost for T period is ${C}_{0}.$

3.1.3. Raw material holding cost

Raw material holding cost is the cost incurred to maintain raw materials. Its function is the following:

${V}_{3} = (1-\alpha )D{C}_{raw}$

(3)

${V}_{3}$ represents average raw material holding cost, which equals to purchase quantity and unit cost of raw materials.

3.1.4. Manufacturing cost

Manufacturing cost is the cost for production activities. Its function is determined by:

${V}_{4} = (1-\alpha )D{C}_{n}$

(4)

${V}_{4}$ represents average manufacturing cost, which equals to manufacturing quantity and unit manufacturing cost.

3.1.5. Inventory costs of raw material and new products

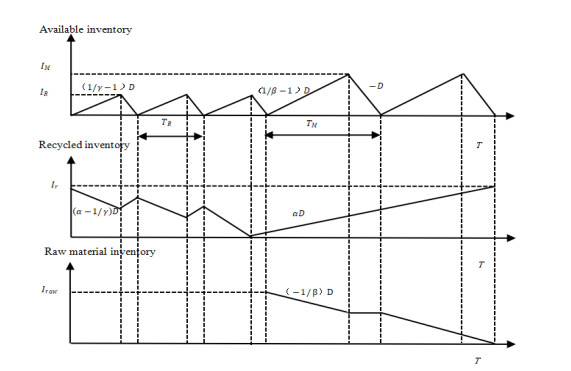
A period T is composed of $n$ manufacturing periods ${T}_{n}$ and $m$ remanufacturing periods ${T}_{m}$ . The inventory statuses are shown in Figure 2 ^[75].

Figure 2. Inventory statuses (Note: m = 3 and n = 2. Here is just an example).

DownLoad: Full-Size Img PowerPoint

Remanufacturing process is set before manufacturing process, because the value of recycled products decreases gradually with the shelving time in a short life cycle. Remanufacturing products inventory builds up at a rate of $(1/\mathrm{\gamma }-1)\mathrm{D}$ units per unit of time and stops at its peak ${I}_{\mathrm{R}}$ ; recycled products inventory decreases at a rate of $(\mathrm{\alpha }-1/\mathrm{\gamma })\mathrm{D}$ . Then manufacturing process begins, new products inventory builds up at a rate of $(1/\mathrm{\beta }-1)\mathrm{D}$ units per unit of time and stops at its peak ${I}_{\mathrm{M}}$ ; simultaneously, raw material inventory decreases at the rate of $(1/\mathrm{\beta })\mathrm{D}$ (as shown in Figure 2).

According to above analysis, the related formulas are listed below:

$T = m {T}_{m}+n{T}_{n}$

(5)

$mD{T}_{m} = \alpha DT , m{T}_{m} = \alpha T$

(6)

$nD{T}_{n} = (1-\alpha )DT , n{T}_{n} = (1-\alpha )T$

(7)

After simple deduction, the following can be gained:

${I}_{raw}$ is the maximum raw material inventory:

${I}_{raw} = nD{T}_{M} = (1-\alpha )DT$

(8)

${I}_{M}$ is the maximum new products inventory:

${I}_{M} = (1-\beta )(1-\alpha )DT/n$

(9)

Then the inventory costs of raw material and new products ${V}_{5}$ are:

${V}_{5} = {\frac{1}{2}\left(\beta +n-1\right)h}_{raw}{I}_{raw}{T}_{n}\frac{1}{T}+\frac{1}{2}{h}_{s}{I}_{M}n{T}_{n}\frac{1}{T}$

$= \frac{1}{2n}{\left(\beta +n-1\right)h}_{raw}{(1-\alpha )}^{2}DT+\frac{1}{2n}{h}_{s}\left(1-\beta \right){\left(1-\alpha \right)}^{2}DT$

(10)

3.2. Cost of remanufactured products

Recycled products, like raw materials, are deemed as a kind of production resource. If their price is higher than production cost, they will not be economically recycled. The quality level of recycled products can affect recycling rate, buyback, and remanufacturing cost.

Recycling rate $d$ is related to the required minimum quality level of recycled products $q$ . If we improve the required minimum quality level $q$ , the recycling rate $d$ will decrease, and vice versa. With a constant demand rate $D$ , recycling rate is defined as:

$d = \alpha D$

(11)

Marginal recycling rate is the following ^[70]:

$\alpha = b{e}^{-\varphi q}$

(12)

$b$ and ${\rm{ \mathsf{ φ} }}$ are parameters applied in different conditions.

Based on model assumptions, required minimum quality level $q$ obeys standard normal distribution, $q\sim N\left(0.1\right)$ , $x$ is the quality level of recycled products, $q < x < 1.$ The probability density function is:

$X(x) = \left\{\begin{array}{l}{\frac{1}{\sqrt{2\pi }}e}^{-{x}^{2}/2}, &q < x < 1\\ 0,& others\end{array}\right.$

(13)

3.2.1. Setup cost for remanufacturing

At each cycle length T, remanufacturing incurs a one-time production setup cost per unit time and it is given by:

${\mathrm{V}}_{6} = m{S}_{1}/T$

(14)

${V}_{6}$ represents average setup cost for remanufacturing.

3.2.2. Buyback cost

Buyback cost ratio p (related to different quality level x) is the ratio of unit buyback cost to unit production cost of new product (here production cost is defined as manufacturing cost ${C}_{n}$ plus raw materials cost ${C}_{raw}$ ). Buyback cost ratio is the following ^[70]:

$p = a{e}^{-\theta (1-x)}$

(15)

Expected function of buyback cost ratio is:

$E\left(p\right) = {\int }_{-\infty }^{+\infty }{\frac{1}{\sqrt{2\pi }}e}^{-{x}^{2}/2}{ae}^{-\theta \left(1-x\right)}dx$

$= a{e}^{\frac{{\theta }^{2}-2\theta }{2}}{\int }_{q}^{1}{\frac{1}{\sqrt{2\pi }}e}^{-\frac{{(x-\theta )}^{ \ \ \ 2}}{2}}dx = a{e}^{\frac{{\theta }^{2}-2\theta }{2}}\left[\varnothing \left(1-\theta \right)-\varnothing \left(q-\theta \right)\right]$

(16)

Buyback cost function is determined by:

${V}_{7} = d({C}_{n}+{C}_{raw})E\left(p\right)$

$= \alpha b{e}^{-\varphi q+({\theta }^{2}-2\theta )/2}\left[\varnothing \left(1-\theta \right)-\varnothing \left(q-\theta \right)\right]D({C}_{n}+{C}_{raw})$

(17)

${V}_{7}$ represents average buyback cost, which consists of ${C}_{n}$ , ${C}_{raw}$ , $E\left(p\right)$ , and $d$ .

The reason why buyback cost is defined according to production cost is that recycled products are assumed to be a kind of raw materials. If we improve the required minimum quality level, the buyback cost will increase, and vice versa.

3.2.3. Remanufacturing cost

Similar to buyback cost function, remanufacturing cost ratio $s$ (related to different quality level x) is the ratio of unit remanufacturing cost to unit manufacturing cost of new product. Remanufacturing cost ratio is the following ^[68]:

$s = c{e}^{\delta (1-x)}$

(18)

Expected function of remanufacturing cost ratio is the following ^[75]:

$E\left(s\right) = {\int }_{-\infty }^{+\infty }{\frac{1}{\sqrt{2\pi }}e}^{-{x}^{2}/2}c{e}^{\delta \left(1-x\right)}dx$

$= c{e}^{\delta }{\int }_{q}^{1}{\frac{1}{\sqrt{2\pi }}e}^{-\frac{{x}^{2}}{2-\delta x}}dx = c{e}^{\frac{{\delta }^{2}+2\delta }{2}}\left[\varnothing \left(1+\delta \right)- \varnothing \left(q+\delta \right)\right]$

(19)

If we improve the required minimum quality level, the remanufacturing cost will decrease, and vice versa. Remanufacturing cost function is determined by:

${V}_{8} = d{C}_{n}E\left(s\right)$

$= cb{e}^{-\varphi q+({\delta }^{2}-2\delta )/2}\left[{e}^{\delta -\left(\delta +\lambda \right)q}-{e}^{-\lambda }\right]\left[\varnothing \left(1+\delta \right)-\varnothing \left(q+\delta \right)\right]D{C}_{n}$

(20)

${V}_{8}$ represents average remanufacturing cost, which consists of ${\mathrm{C}}_{\mathrm{n}}$ , $\mathrm{E}\left(\mathrm{s}\right)$ , and $\mathrm{d}$ .

3.2.4. Inventory costs of recycled products and remanufacturing products

${I}_{r} \ \mathrm{i}\mathrm{s}$ the maximum recycled products inventory:

${I}_{r} = \alpha \left[\left(1-\alpha \right)+\frac{\alpha \left(1-\gamma \right)}{m}\right]DT$

(21)

${I}_{R}$ is the maximum remanufacturing products inventory:

${I}_{R} = (1-\gamma )\alpha DT/m$

(22)

Then the inventory costs of recycled products and remanufacturing products ${V}_{9}$ are: ${V}_{9} = \frac{1}{2}{h}_{s}{I}_{R}m{T}_{m}\frac{1}{T}+\frac{1}{2}{h}_{r}{I}_{r}T\frac{1}{T}$

$= \frac{1}{2m}{h}_{s}\left(1-\gamma \right){\alpha }^{2}DT+\frac{1}{2}{h}_{r}\left[\alpha \left(1-\alpha \right)+\frac{1}{m}{\alpha }^{2}\left(1-\gamma \right)\right]DT$

(23)

3.3. Incentive-compatibility functions

Incentive-compatibility theory can avoid the agent to damage the principal's interests for their own benefits through various incentive strategies and ensure the agent act in accordance with the wishes of the principal, so that both parties tend to maximize their utilities ^[76].

According to above definition, incentive-compatibility theory consists of two parts: incentive and compatibility ^[77]. In this paper, the agent is set as manufacturer, and the principal is set as government. In order to undertake CER in production activities, manufacturer produces green products through green investment. In order to incent and guide manufacturer to set a higher green investment level, improve the implementation effect of recycling and remanufacturing, and achieve the purpose of environmental protection, government adopts differential weighting subsidy policy for manufacturer and consumers. Therefore, green investment is compatibility and government subsidy is incentive.

3.3.1. Incentive function

Government plays an important role in the formation and development of closed loop supply chain ^[78]. The operation of closed loop supply chain can be optimized and overall environmental benefits can be maximized by government subsidy incentive ^[72].

Government implements differential weight subsidy incentive for manufacturer and consumers purchasing remanufactured products according to model assumptions. With different quality levels of recycled products, the total subsidy amount for unit remanufactured product is $r = {p}_{r}t\left(q-{q}_{s}\right)/q$ ^[24]. The allocation weights for consumers and manufacturer are $w$ and $1-w$ , so the total subsidy amount for manufacturer producing remanufactured products is:

${S}_{m} = \left(1-w\right)rd = \left(1-w\right){p}_{r}tb{e}^{-\varphi q}D\left(q-{q}_{s}\right)/q$

(24)

The total subsidy amount for consumers purchasing remanufactured products is:

${S}_{c} = wrd = w{p}_{r}tb{e}^{-\varphi q}D\left(q-{q}_{s}\right)/q$

(25)

3.3.2. Compatibility function

Manufacturer undertakes corporate environmental responsibility and produces green products through green technology investment. Green investment cost is a convex function of investment level $e$ . The average green investment cost is the following ^[79]:

${V}_{10} = \pi {e}^{2}/T$

(26)

3.4. Average gross profit

The average gross profit of the green closed loop supply chain system considering only CER without government subsidy is:

$AP = {p}_{n}{D}_{n}+{p}_{r}{D}_{r}-{V}_{1}-{V}_{2}-{V}_{3}-{V}_{4}-{V}_{5}-{V}_{6}-{V}_{7}-{V}_{8}-{V}_{9}-{V}_{10}$

$= {p}_{n}\left({\alpha }_{n}-{\tau }_{1}{p}_{n}+{\tau }_{2}{p}_{r}-\mu \sqrt{wr}+l\sqrt{e}\right)+{p}_{r}\left({\alpha }_{r}-{\tau }_{1}{p}_{r}+{\tau }_{2}{p}_{n}+\mu \sqrt{wr}+l\sqrt{e}\right)$

$-n{S}_{1}/T-{C}_{o}/T-\left(1-\alpha \right)\left[{\alpha }_{n}+{\alpha }_{r}+\left({\tau }_{2}-{\tau }_{1}\right)\left({p}_{n}+{p}_{r}\right)+2l\sqrt{e}\right]\left({C}_{n}+{C}_{raw}\right)$

$-\left[\frac{\beta +n-1}{2n}{h}_{raw}+\frac{{h}_{s}}{2n}\left(1-\beta \right)\right]\left[{\alpha }_{n}+{\alpha }_{r}+\left({\tau }_{2}-{\tau }_{1}\right)\left({p}_{n}+{p}_{r}\right)+2l\sqrt{e}\right]T{(1-\alpha )}^{2}$

$-m{S}_{1}/T-\alpha b{e}^{-\varphi q+({\theta }^{2}-2\theta )/2}\left[{\alpha }_{n}+{\alpha }_{r}+\left({\tau }_{2}-{\tau }_{1}\right)\left({p}_{n}+{p}_{r}\right)+2l\sqrt{e}\right]({C}_{n}+{C}_{raw})$

$\left[\varnothing \left(1-\theta \right)-\varnothing \left(q-\theta \right)\right]-cb{e}^{-\varphi q+({\delta }^{2}-2\delta )/2}\left[{e}^{\delta -\left(\delta +\lambda \right)q}-{e}^{-\lambda }\right]\left[\varnothing \left(1+\delta \right)-\varnothing \left(q+\delta \right)\right]$

$\left[{\alpha }_{n}+{\alpha }_{r}+\left({\tau }_{2}-{\tau }_{1}\right)\left({p}_{n}+{p}_{r}\right)+2l\sqrt{e}\right]{C}_{n}-\left[{\alpha }_{n}+{\alpha }_{r}+\left({\tau }_{2}-{\tau }_{1}\right)\left({p}_{n}+{p}_{r}\right)+2l\sqrt{e}\right]$

$\left[\frac{{h}_{s}}{2m}\left(1-\gamma \right){\alpha }^{2}+\frac{{h}_{r}}{2}\alpha \left(1-\alpha \right)+\frac{{h}_{r}}{2m}{\alpha }^{2}\left(1-\gamma \right)\right]T-\pi {e}^{2}/T$

(27)

The average gross profit of the green closed loop supply chain system considering CER and government differential weight subsidy is:

$APG = {p}_{n}{D}_{n}+{p}_{r}{D}_{r}-{V}_{1}-{V}_{2}-{V}_{3}-{V}_{4}-{V}_{5}-{V}_{6}-{V}_{7}-{V}_{8}-{V}_{9}-{V}_{10}+{S}_{m}$

$= {p}_{n}\left({\alpha }_{n}-{\tau }_{1}{p}_{n}+{\tau }_{2}{p}_{r}+l\sqrt{e}\right)+{p}_{r}\left({\alpha }_{r}-{\tau }_{1}{p}_{r}+{\tau }_{2}{p}_{n}+l\sqrt{e}\right)$

$-n{S}_{1}/T-{C}_{o}/T-\left(1-\alpha \right)\left[{\alpha }_{n}+{\alpha }_{r}+\left({\tau }_{2}-{\tau }_{1}\right)\left({p}_{n}+{p}_{r}\right)+2l\sqrt{e}\right]\left({C}_{n}+{C}_{raw}\right)$

$\left[\frac{{h}_{s}}{2m}\left(1-\gamma \right){\alpha }^{2}+\frac{{h}_{r}}{2}\alpha \left(1-\alpha \right)+\frac{{h}_{r}}{2m}{\alpha }^{2}\left(1-\gamma \right)\right]T-\pi {e}^{2}/T+\left(1-w\right){p}_{r}tb{e}^{-\varphi q}$

$\left[{\alpha }_{n}+{\alpha }_{r}+\left({\tau }_{2}-{\tau }_{1}\right)\left({p}_{n}+{p}_{r}\right)+2l\sqrt{e}\right]\left(q-{q}_{s}\right)/q$

(28)

3.5. Fuzzy chance constrained clarifications

Fuzzy Chance Constrained Programming (FCCP) is an uncertain mathematical programming method based on possibility theory and fuzzy set theory, which provides a powerful tool for solving uncertain problems ^[80]. Its main idea is to transform the fuzzy chance constraints into equivalent deterministic forms ^[81]. Fuzzy chance constrained programming is used to solve the problems of uncertain demand for new products and remanufactured products in this paper. The triangular fuzzy number of potential demand for new products and remanufactured products are defined respectively as ${d}_{n} = ({d}_{n1}, {d}_{n2}, {d}_{n3})$ and ${d}_{r} = ({d}_{r1}, {d}_{r2}, {d}_{r3})$ . Their fuzzy membership functions are as follows:

${U}_{\stackrel{~}{{d}_{n}}}\left(t\right) = \left\{\begin{array}{l}\frac{t-{d}_{n1}}{{d}_{n2}-{d}_{n1}}, t\in \left[{d}_{n1}, {d}_{n2}\right]\\ \frac{{d}_{n3}-t}{{d}_{n3}-{d}_{n2}}, t\in \left[{d}_{n2}, {d}_{n3}\right]\\ 0 \ \ \ \ , \text{ others}\end{array}\right.{\text{,}U}_{\stackrel{~}{{d}_{r}}}\left(t\right) = \left\{\begin{array}{l}\frac{t-{\mathrm{d}}_{\mathrm{r}1}}{{\mathrm{d}}_{\mathrm{r}2}-{\mathrm{d}}_{\mathrm{r}1}}, t\in \left[{\mathrm{d}}_{\mathrm{r}1}, {d}_{r2}\right]\\ \frac{{d}_{r3}-t}{{d}_{r3}-{d}_{r2}}, t\in \left[{d}_{r2}, {d}_{r3}\right]\\ 0 \ \ \ \ , \text{others}\end{array}\right.$

(29)

According to the clear definition and lemma, we can get the following:

$\left\{\begin{array}{l}{X}_{di}\ge \left(1-j\right) \cdot {d}_{n1}+j{d}_{n2}\\ {X}_{di}\le \left(1-j\right) \cdot {d}_{n3}+j{d}_{n2}\\ Pos\{{X}_{di} = {d}_{n}\ge j\}\end{array}\right., \left\{\begin{array}{l}{X}_{id}\ge \left(1-k\right) \cdot {d}_{r1}+k{d}_{r2}\\ {X}_{id}\le \left(1-k\right) \cdot {d}_{r3}+k{d}_{r2}\\ Pos\{{X}_{id} = {d}_{r}\ge k\}\end{array}\right.$

(30)

4. Solution techniques

Based on the above analysis, the optimization task this model deals with is a non-linear optimization issue with mixed continuous/integer variables. Exact algorithms and meta-heuristic algorithm are often used to solve this kind of problems ^[82]. Among them, meta-heuristic algorithms always have faster operation speed, but the results of their solution are approximate optimal solution ^[83]; an exact algorithm can find the most accurate solution, but it always takes more time.

Among many meta-heuristic algorithms, GA is widely used because of its powerful global search ability ^[24]. Most researches use GA to obtain approximate optimal solutions for functional optimization, facility location, and vehicle routing optimization and so on ^[84]. Afzal et al. ^[85] used GA to solve a kind of function optimization problem. Guo et al. ^[24] verified the correlation model reliability by GA algorithm, and obtained approximate optimal solutions with high quality.

Based on this, CPLEX is used in this paper to find the optimal solution of the calculating example, and also the validity of the model is verified. However, when the calculation scale is large, the solution time of CPLEX is very long, or the solution cannot be obtained. Therefore, this paper also uses GA to find the approximate optimal solution. By comparing the calculation results of CPLEX and GA in a small-scale case, the effectiveness of GA algorithm is verified.

4.1. Genetic algorithm

As one of the evolutionary computation techniques, GA has been receiving great attention and successfully applied for combinatorial optimization problems, various integrated production, distribution planning problems and so on ^[62,86]). Genetic algorithm is an intelligent optimization algorithm based on genetic mechanism and natural selection, which can make the population continuously evolve through replication, crossover and mutation operations until the optimal solution is obtained ^[87,88].

The main operation steps of GA are as follows:

Step 1: Chromosome coding and initialization. In this paper, chromosome genes number is set as 6, maximum iteration number is set as 200, and population size is set as 50. Adopt binary coding to generate 0/1 initial population randomly, as shown in Table 2.

Table 2. Genetic algorithm initial population.

population	binary coding
population	$g$	$m$	$n$	$T$	${P}_{n}$	${P}_{r}$
1	10…1	01	10	10…0	11…1	01…1
2	01…0	10	01	01…1	10…0	01…1
…	…	…	…	…	…	…
49	11…1	11	10	10…1	10…1	10…0
50	10…1	01	01	01…1	01…0	11…0

| Show Table

DownLoad: CSV

Step 2: Calculate fitness values. The fitness value of a chromosome reflects the probability of being selected. According to fitness function $\mathrm{f}\left(\mathrm{x}\right) = object/1000$ to calculate fitness value and $object$ is the objective function equations (27) ~ (28) in this paper.

Step 3: Individual selection. Roulette wheel method is used for individual selection. The larger the objective function value is, the easier the chromosome is to be selected. Individual selection probability is:

${p}_{i} = {f}_{i}/{f}_{sum}$

(31)

Step 4: Crossover and variation. The process of crossover and mutation is shown in Table 3. In this paper, the crossover probability and mutation probability are set as 0.75 and 0.03.

Table 3. Genetic algorithm crossover/mutation process.

population	crossover				mutation
Parent 1	1	0	1	…	0	1	0
Parent 2	0	1	0	…	1	0	1
Child 1	0	0	1	…	0	1	0
Child 2	1	1	0	…	1	1	0

| Show Table

DownLoad: CSV

Step 5: Stop condition. If the termination condition (maximum iteration number) is met, output the optimal solution is; otherwise, return to step 2.

5. Numerical experiments

5.1. Numerical results

According to the actual situation of the manufacturing industry and relevant literature research, parameter values are set and shown in Table 4 ^[68,24,70].

Table 4. Genetic algorithm crossover/mutation process.

parameter	value	parameter	value	parameter	value	parameter	value
${h}_{s}$	2	${h}_{r}$	0.3	${h}_{raw}$	0.2	${C}_{n}$	25
${C}_{raw}$	15	${C}_{O}$	850	${S}_{1}$	1500	${S}_{2}$	1500
$\mathrm{a}$	0.9	$\mathrm{b}$	0.9	$\mathrm{c}$	0.1	$\mathrm{\beta }$	0.5
$\mathrm{\gamma }$	0.6	${d}_{n1}$	715	${d}_{n2}$	863	${d}_{n3}$	1020
${d}_{r1}$	468	${d}_{r2}$	615	${d}_{r3}$	736	${\rm{ \mathsf{ φ} }}$	2
${\tau }_{1}$	2.5	${\tau }_{2}$	1.5	${q}_{s}$	0.2	$\mathrm{\mu }$	75
$\mathrm{k}$	65	$\mathrm{\pi }$	70	$\mathrm{e}$	3	$\mathrm{t}$	0.9
$\mathrm{w}$	0.35	$\mathrm{\sigma }$	1.1

| Show Table

DownLoad: CSV

5.1.1. Optimal decision under uncertain environment

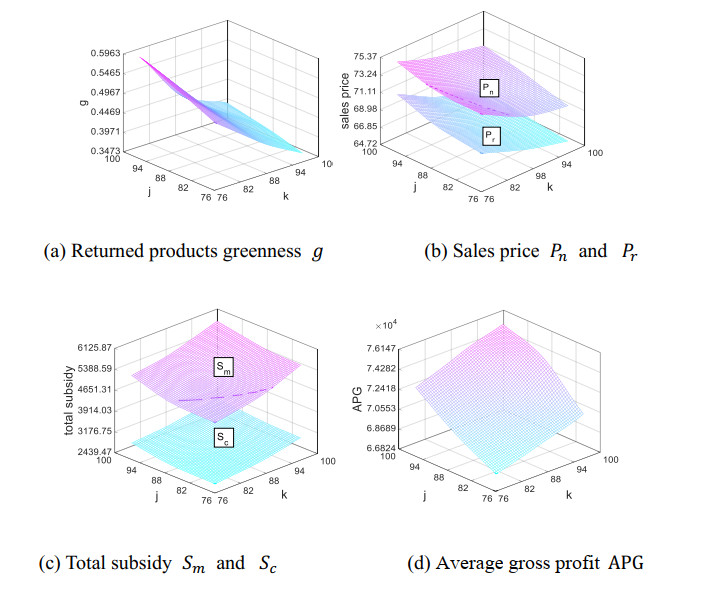
In this paper, 10% range is used to assign values of 76%, 86% and 96% to $j$ and $k$ respectively, and Matlab software is used to write GA and CPLEX codes to solve calculation example comparatively. The difference ratio of optimal fitness value between GA and CPLEX is $gap = \left|{APG}_{\mathrm{G}\mathrm{A}}-{APG}_{\mathrm{C}\mathrm{P}\mathrm{L}\mathrm{E}\mathrm{X}}\right|/{APG}_{\mathrm{G}\mathrm{A}}$ .

The calculation results are shown in Table 5 and . For further study optimal decisions under different confidence levels, the variation trend are shown in under the condition that $j$ and $k$ gradually increase from 76% to 96%.

Table 5. Optimal decision under different confidence levels (GA).

confidence level		GA
$j$	$k$	$g$	$m$	$n$	${P}_{n}$	${P}_{n}$	${APG}_{\mathrm{G}\mathrm{A}}$	${S}_{m}$	${S}_{c}$
	76%	0.5036	1	1	73.26	68.46	67815.07	4697.36	2529.35
76%	86%	0.4204	2	1	70.64	66.58	69046.85	4985.72	2684.62
	96%	0.3553	3	1	69.58	65.27	70383.08	5563.49	2995.73
	76%	0.5456	1	3	73.45	69.14	69873.64	4758.65	2562.35
86%	86%	0.4452	2	3	71.37	67.15	71467.36	5041.83	2714.83
	96%	0.3817	3	3	70.95	65.93	73972.59	5657.45	3046.32
	76%	0.5895	1	4	74.82	70.82	72586.37	5168.24	2782.90
96%	86%	0.4537	2	4	73.14	68.21	74163.42	5437.26	2927.76
	96%	0.4024	3	4	72.08	66.74	75452.63	5925.73	3190.78

| Show Table

DownLoad: CSV

Table 6. Comparison of optimal decision GA and CPLEX objective function values.

confidence level			GA		CPLEX		$gap$ (%)
$j$	$k$	$g$	${APG}_{\mathrm{G}\mathrm{A}}$	$Time\left(s\right)$	${APG}_{CPLEX}$	$Time\left(s\right)$
	76%	0.5045	67815.07	22.15	67804.21	22.56	0.16
76%	86%	0.4219	69046.85	24.61	69037.18	21.67	0.14
	96%	0.3546	70383.08	25.45	70370.42	20.78	0.17
	76%	0.5457	69873.64	26.57	69863.16	22.57	0.15
86%	86%	0.4473	71467.36	22.89	71455.21	21.56	0.16
	96%	0.3802	73972.59	22.36	73962.23	20.13	0.14
	76%	0.5875	72586.37	26.67	72573.30	23.21	0.18
96%	86%	0.4532	74163.42	25.89	74152.29	22.34	0.15
	96%	0.4028	75452.63	22.15	75439.82	21.89	0.17

| Show Table

DownLoad: CSV

Figure 3. The effect of different

$j$ and

$k$ on the optimal decision.

DownLoad: Full-Size Img PowerPoint

It can be seen from Table 5 and Table 6 that:

(1) The maximum difference ratio between CPLEX and GA is 0.18%, which indicates that GA algorithm is not trapped into local optimal solution, thus verifying the proposed algorithm's validity and model's reliability. In this numerical example, when $j$ and $k$ are 96%, $m$ is 3, $n$ is 4, ${P}_{n}$ and ${P}_{r}$ are 72.08 and 66.74, the average gross profit $APG$ reaches the maximum value 75452.63. At this moment, ${S}_{m}$ and ${S}_{c}$ are 5925.73 and 3190.78 respectively.

(2) By comparing the relationship between running time and the optimal solution, it is proved to have a certain accuracy and efficiency, so as to verify the validity of the algorithm and the credibility of the model.

(3) In actual enterprise production, enterprises often need to solve large-scale cost or profit problems, and expect to get a better cost or profit solution to reduce costs as soon as possible. However, if the scale of data is too large, CPLEX cannot find the feasible solution in reasonable time, which may cause the loss of its practical application value, therefore, the complementary solution of GA and CPLEX in this paper is more applicable.

It can be concluded from figure 3 that:

(1) When $j$ is certain, as $k$ increases gradually, $g$ , ${P}_{n}$ and ${P}_{r}$ are decreasing; ${S}_{m}$ , ${S}_{c}$ and $APG$ are increasing gradually. That is to say, when $j$ is certain, with the increase of $k$ , recycled products greenness decreases, sales price of new products and remanufactured products decreases, the subsidy amount for manufacturer and consumers gradually increases, and the average total profit increases gradually. That is because, with the increase of $k$ , manufacturer's subsidy amount increases gradually, so the average total profit increases.

(2) When $k$ is certain, as $j$ increases gradually, $g$ is increasing, ${P}_{n}$ , ${P}_{r}$ , ${S}_{m}$ , ${S}_{c}$ and $APG$ is increasing gradually, that is to say, when $k$ is certain, with the increase of $j$ , recycled products greenness increases, sales prices of new products and remanufactured products increases, the subsidy amount for manufacturers and consumers increases, and the average total profit increases gradually. That is because, with the increase of $j$ , average raw material procurement operating cost decreases gradually, so the average total profit increases.

(3) With the increase of $k$ , enterprises should produce more remanufacturing products and increase economic benefits by increasing government subsidy. With the increase of $j$ , enterprises should produce more new products and increase economic benefits by reducing raw material procurement cost. Enterprises can make optimal recycling, production, and sales decisions according to potential demand, and hence gradually increase the gross profit.

5.1.2. Optimal decision under no government subsidy

In the case of considering CER alone without government subsidy, we study the effect of green investment level on gross profit, recycled products greenness, recycling rate, and manufacturer's enthusiasm for green investment.

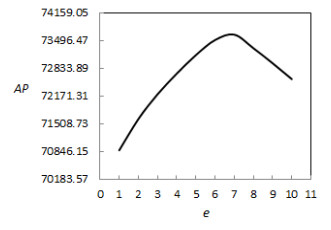
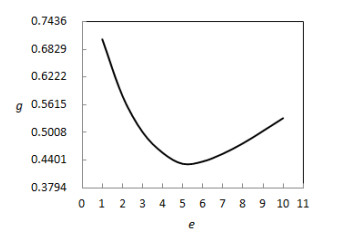
It can be concluded from figure 4 and figure 5 that:

Figure 4. The effect of

$e$ on

$AP$ .

DownLoad: Full-Size Img PowerPoint

Figure 5. The effect of

$e$ on

$g$ .

DownLoad: Full-Size Img PowerPoint

(1) When $e < 6.9$ , as $e$ increases, $AP$ goes up gradually; However, when $e > 6.9$ , as $e$ increases further, $AP$ goes down instead. This is because, with the increase of $e$ , green investment cost increases greatly, so $AP$ decreases gradually.

(2) When $e < 5.3$ , as $e$ increases, $g$ goes down and $d$ goes up gradually; However, when $e > 5.3$ , as $e$ increases further, $g$ goes up instead. This is because, the higher green investment cost pushes up the sales price, and the growth rate of market demand decreases brought by green investment, so $g$ goes up instead.

(3) In the case of no government subsidy and only considering CER, a higher green investment level will make a decrease in average gross profit and recycling rate, and an increase in recycled products greenness, which leads to a lower green investment level and an insignificant effect on environmental protection.

5.1.3. Optimal decision under government differential weighting subsidy

In the case of considering CER and government differential weighting subsidy, based on incentive-compatibility theory, we study the reasonable subsidy allocation weight set by government to effectively incent manufacturer to set a higher green investment level, in order to achieve the effect of incentive-compatibility and the purpose of environmental protection.

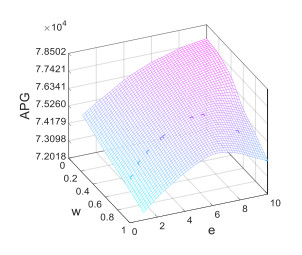
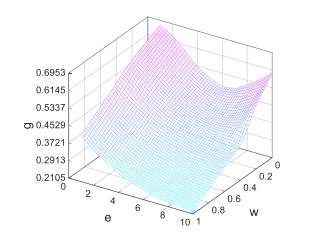
It can be concluded from figure 6 and figure 7 that:

Figure 6. The effect of

$w$ and

$e$ on

$APG$ .

DownLoad: Full-Size Img PowerPoint

Figure 7. The effect of

$w$ and

$e$ on

$g$ .

DownLoad: Full-Size Img PowerPoint

(1) When $0 < \mathrm{w} < 0.41$ , with the increase of $e$ , $APG$ increases gradually. Government subsidy has a positive effect on improving the green investment level of manufacturer, and the incentive effect is significant; However, when $0.41 < \mathrm{w} < 1$ , with the increase of $e$ , $APG$ firstly goes up and then goes down. Although the optimal value of $e$ is improved, the incentive effect is not high.

(2) When $0.34 < \mathrm{w} < 1$ , with the increase of $e$ , $g$ decreases and $d$ increases gradually. Manufacturer is incited to enhance the green investment level, and the market demand for green products is increased gradually. The incentive effect is significant; However, when $0 < \mathrm{w} < 0.34$ , with the increase of $e$ , $g$ firstly goes down and then goes up, and $d$ firstly goes up and then goes down. Although the optimal value of $g$ decreases, the incentive effect is not high.

(3) Based on above analysis, government differential weighting subsidy can reduce the financial burden of enterprises' green investment and expand the market demand for green products. When government sets the subsidy weight for consumer as 0.34~0.41, with the increase of green investment level, average gross profit increases, recycled products greenness decreases, and recycling rate increases gradually, which continuously promotes enterprises to develop a higher green investment level, achieve the effect of incentive-compatibility and the purpose of environmental protection.

5.1.4. Effect comparison before and after incentive-compatibility theory

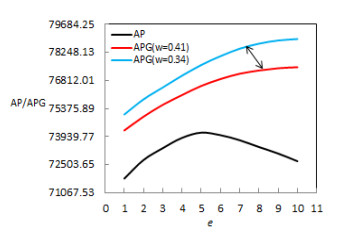
It can be concluded from figure 8 and figure 9 that:

Figure 8. The effect of

$e$ on

$AP$ and

$APG$ .

DownLoad: Full-Size Img PowerPoint

Figure 9. The effect of

$e$ on

$g$ .

DownLoad: Full-Size Img PowerPoint

(1) Based on incentive-compatibility theory, when government sets the subsidy weight for consumer as 0.34 < $w$ < 0.41 (the corresponding subsidy weight for manufacturer as 0.59 < $1-w$ < 0.66).

(2) Compared with before the implementation of incentive-compatibility, with the increase of green investment level $e$ , average gross profit $APG$ increases, recycled products greenness $g$ decreases, and recycling rate $d$ increases gradually, which incite enterprises to continuously enhance the green investment level.

(3) Therefore, by formulating reasonable subsidy policies, the government can reduce the financial burden of enterprises' green investment and expand the market demand for green products.

5.2. Discussion (Managerial insights and main achievements)

Based on above calculating results and analysis, managerial insights are rendered as the following:

(1) Under uncertain environment, enterprises can adopt the following methods to optimize the green closed loop supply chain system (GCL-SCS):

● When the confidence level of potential demand for new products is certain, with the increase of confidence level of potential demand for remanufactured products, enterprise should recycle the used products with lower greenness, reduce the sales prices of new products and remanufactured products, and increase recycling rate and remanufacturing lot, so as to improve the gross profit.

● When the confidence level of potential demand for remanufactured products is certain, with the increase of the confidence level of potential demand for new products, enterprise should recycle the used products with higher greenness, increase the sales price of new products and remanufactured products, decrease recycling rate, and increase manufacturing lot, so as to improve the gross profit.

(2) In the case of only CER with no government subsidy, enterprises can optimize the green closed loop supply chain system by the following methods:

● In the case of only green investment, a higher green investment level will reduce the gross profit and recycling rate. Therefore, enterprises should set a lower level of green investment to avoid a higher green investment cost.

● In the case of only green investment, the optimal green investment level of the enterprise should be kept within a certain range, which is 5.3-6.9 in the calculating example of this paper.

(3) In the case of considering CER and government differential weighting subsidy, based on incentive-compatibility theory, government can optimize the green closed loop supply chain system by the following methods:

● With the increase of green investment level, recycled products' greenness decreases, recycling rate increases, and the average gross profit increases gradually. Through the formulation of reasonable subsidy system, the government can reduce the financial burden of enterprises' green investment. When the weight of government's subsidy to consumers and manufacturers is controlled within a certain range, which are 0.34-0.41 and 0.59-0.66 in the calculating example of this paper.

● By formulating the reasonable subsidy policy, government can expand the market demand for green products, incent and guide enterprises to develop a higher green investment level, improve the implementation effect of recycling and remanufacturing, and achieve the optimal effect of environmental protection.

The main achievements could be the following:

(1) Under uncertain environments of market demands and quality level of recycled products, two gross profit models of green closed loop supply chain system are constructed under no government subsidy and government differential weight subsidy considering CER.

(2) Guiding enterprises to make optimal recycling, production, and sales decisions when faced with uncertain environments.

(3) Based on incentive compatibility theory, this paper studies the optimal subsidy allocation policy and green investment level when both government and enterprises tended to maximize utility.

6. Conclusions

Under uncertain environment of market demand and recovery quality, based on incentive-compatibility theory, this paper studies the optimal subsidy allocation policy and green investment level when both government and enterprises tend to maximize utility. FCCP method is used to solve the fuzzy constraint problem; GA and CPLEX are used to solve a calculating example's approximate optimal solution of the model in this paper.

From this research we can get the following results: (1) Different levels of potential demand will affect enterprises' optimal recycling, production, and sales decisions; (2) In the case of considering CER without government subsidy, enterprises' enthusiasm for green investment is low and environmental protection effect is not obvious; (3) In the case of considering CER and government differential weighting subsidy, based on incentive- compatibility theory, reasonable subsidy and green investment can reduce the financial burden of enterprises' green investment effectively, incent enterprises to set a higher green investment level continuously, improve recycling rate and gross profit, and hence make the green closed loop supply chain reach the optimal state.

This study can provide reference for enterprises to make optimal recycling, production, and sales decisions under uncertain environments and provide quantifiable suggestions for government to set reasonable subsidy level, so as to effectively promote enterprises' enthusiasm for green investment and improve the recycling rate and gross profit in the green closed loop supply chain.

Limitations and further research:

(1) Under uncertain environment, this paper only studies offline distribution channels. Further research can consider online and offline sales channels in the e-commerce environment.

(2) This paper focuses on the recycling and manufacturing/remanufacturing of green products. Further research can consider more activities such as transportation and storage.

(3) This paper assumes that product shortage and surplus are not taken into account. Further study can consider the effect of product shortage or surplus on the optimal decisions in green closed loop supply chain.

Acknowledgments

This research is supported by the National Natural Science Foundation, China (No. 71631007, 71471110), Shanghai Science and Technology Innovation Action Plan (No.16DZ1201402), Capacity Building Project of Shanghai Science and Technology Commission (No.16040501500), and Grant-in-Aid for Scientific Research (C) of Japan Society of Promotion of Science (JSPS) (19K12148).

Conflict of interest

The authors declare there is no conflict of interest.

References

[1]	M. S. Atabaki, M. Mohammadi, B. Naderi, New robust optimization models for closed-loop supply chain of durable products: Towards a circular economy, Comput. Ind. Eng., 146 (2020), 106520. https://doi.org/10.1016/j.cie.2020.106520 doi: 10.1016/j.cie.2020.106520
[2]	B. Khorshidvand, H. Soleimaniab, S. Sibdaric, M. M. S. Esfahanid, A hybrid modeling approach for green and sustainable closed-loop supply chain considering price, advertisement and uncertain demands, Comput. Ind. Eng., 157 (2021), 107326. https://doi.org/10.1016/j.cie.2021.107326 doi: 10.1016/j.cie.2021.107326
[3]	H. Liao, L. Li, Environmental sustainability EOQ model for closed-loop supply chain under market uncertainty: A case study of printer remanufacturing, Comput. Ind. Eng., 149 (2020), 106779. https://doi.org/10.1016/j.cie.2020.106525 doi: 10.1016/j.cie.2020.106525
[4]	R. Dominguez, B. Ponte, S. Cannella, J. M. Framinan, On the dynamics of closed-loop supply chains with capacity constraints, Comput. Ind. Eng., 128 (2019), 91-103. https://doi.org/10.1016/j.cie.2018.12.003 doi: 10.1016/j.cie.2018.12.003
[5]	H. Peng, N. Shen, H. Liao, H. Xue, Q. Wang, Uncertainty factors, methods, and solutions of closed-loop supply chain — A review for current situation and future prospects, J. Clean Prod., 254 (2020), 120032. https://doi.org/10.1016/j.jclepro.2020.120032 doi: 10.1016/j.jclepro.2020.120032
[6]	B. Zhu, B. Wen, S. Ji, R. Qiu, Coordinating a dual-channel supply chain with conditional value-at-risk under uncertainties of yield and demand, Comput. Ind. Eng., 139 (2020), 106181. https://doi.org/10.1016/j.cie.2019.106181 doi: 10.1016/j.cie.2019.106181
[7]	I. I. Almaraj, T. B. Trafalis, An integrated multi-echelon robust closed- loop supply chain under imperfect quality production, Int. J. Prod. Econ., 218 (2019), 212-227. https://doi.org/10.1016/j.ijpe.2019.04.035 doi: 10.1016/j.ijpe.2019.04.035
[8]	L. Wang, Q. Song, Pricing policies for dual-channel supply chain with green investment and sales effort under uncertain demand, Math Comput. Simul., 171 (2020), 79-93. https://doi.org/10.1016/j.matcom.2019.08.010 doi: 10.1016/j.matcom.2019.08.010
[9]	C. Li, L. Feng, S. Luo, Strategic introduction of an online recycling channel in the reverse supply chain with a random demand, J. Clean Prod., 236 (2019), 117683. https://doi.org/10.1016/j.jclepro.2019.117683 doi: 10.1016/j.jclepro.2019.117683
[10]	Y. Dai, L. Dou, H. Song, H. Y. Li, Two-way information sharing of uncertain demand forecasts in a dual-channel supply chain, Comput. Ind. Eng., 169 (2022), 108162. https://doi.org/10.1016/j.cie.2022.108162 doi: 10.1016/j.cie.2022.108162
[11]	X. Y. Zhu, Y. ZH. Cao, J. W. Wu, H. Liu, X. Q. Bei, Optimum operational schedule and accounts receivable financing in a production supply chain considering hierarchical industrial status and uncertain yield, Euro. J. Oper. Res., 302 (2022), 1142-1154. https://doi.org/10.1016/j.ejor.2022.02.008 doi: 10.1016/j.ejor.2022.02.008
[12]	L. J. Zeballos, M. I. Gomes, A. P. Barbosa-Povoa, A. Q. Novaisa, Addressing the uncertain quality and quantity of returns in closed-loop supply chains, Comput. Chem. Eng., 47 (2012), 237-247. https://doi.org/10.1016/j.compchemeng.2012.06.034 doi: 10.1016/j.compchemeng.2012.06.034
[13]	M. Jeihoonian, M. K. Zanjani, M. Gendreaub, Closed-loop supply chain network design under uncertain quality status: Case of durable products, Int. J. Prod. Econ., 183 (2017), Part B, 470-486. https://doi.org/10.1016/j.ijpe.2016.07.023
[14]	J. Heydari, M. Ghasemi, A revenue sharing contract for reverse supply chain coordination under stochastic quality of returned products and uncertain remanufacturing capacity, J. Clean Prod., 197 (2018), 607-615. https://doi.org/10.1016/j.jclepro.2018.06.206 doi: 10.1016/j.jclepro.2018.06.206
[15]	A. Aminipour, Z. Bahroun, M. Hariga, Cyclic manufacturing and remanufacturing in a closed-loop supply chain, Sustain Prod. Consump., 25 (2021), 43-59. https://doi.org/10.1016/j.spc.2020.08.002 doi: 10.1016/j.spc.2020.08.002
[16]	Z. Ghelichi, M. Saidi-Mehrabad, M. S. Pishvaee, A stochastic programming approach toward optimal design and planning of an integrated green biodiesel supply chain network under uncertainty: A case study, Energy, 156 (2018), 661-687. https://doi.org/10.1016/j.energy.2018.05.103 doi: 10.1016/j.energy.2018.05.103
[17]	M. Farrokh, A. Azar, G. Jandaghi, E. Ahmadi, A novel robust fuzzy stochastic programming for closed loop supply chain network design under hybrid uncertainty, Fuzzy Set. Syst., 341 (2018), 69-91. https://doi.org/10.1016/j.fss.2017.03.019 doi: 10.1016/j.fss.2017.03.019
[18]	S. Ahmadi, S. H. Amin, An integrated chance-constrained stochastic model for a mobile phone closed-loop supply chain network with supplier selection, J. Clean Prod., 226 (2019), 988-1003. https://doi.org/10.1016/j.jclepro.2019.04.132 doi: 10.1016/j.jclepro.2019.04.132
[19]	M. Josefa, P. David, P. Raul, The effectiveness of a fuzzy mathematical programming approach for supply chain production planning with fuzzy demand, Int. J. Prod. Econ., 128 (2010), 136-143. https://doi.org/10.1016/j.ijpe.2010.06.007 doi: 10.1016/j.ijpe.2010.06.007
[20]	C. Lima, S. Relvas, A. Barbosa-Póvoab, Designing and planning the downstream oil supply chain under uncertainty using a fuzzy programming approach, Comput. Chem. Eng., 151 (2021), 107373. https://doi.org/10.1016/j.compchemeng.2021.107373 doi: 10.1016/j.compchemeng.2021.107373
[21]	F. Ziya-Gorabi, A. Ghodratnama, R. Tavakkoli-Moghaddam, M. S. Asadi-Lari, A new fuzzy tri-objective model for a home health care problem with green ambulance routing and congestion under uncertainty, Expert Syst. Appl., 201 (2022), 117093. https://doi.org/10.1016/j.eswa.2022.117093 doi: 10.1016/j.eswa.2022.117093
[22]	J. Ghahremani-Nahr, R. Kian, E. Sabetd, A robust fuzzy mathematical programming model for the closed-loop supply chain network design and a whale optimization solution algorithm, Expert Syst. Appl., 116 (2019), 454-471. https://doi.org/10.1016/j.eswa.2018.09.027 doi: 10.1016/j.eswa.2018.09.027
[23]	H. Jafar, R. Pooya, Integration of environmental and social responsibilities in managing supply chains: A mathematical modeling approach, Comput. Ind. Eng., 145 (2020), 106495. https://doi.org/10.1016/j.cie.2020.106495 doi: 10.1016/j.cie.2020.106495
[24]	J. Q. Guo, H. L. Yu, M. Gen, Research on green closed-loop supply chain with the consideration of double subsidy in e-commerce environment, Comput. Ind. Eng., 149 (2020), 106779. https://doi.org/10.1016/j.cie.2020.106779 doi: 10.1016/j.cie.2020.106779
[25]	J. Jian, B. Lia, N. Zhang, J. F. Su, Decision-making and coordination of green closed-loop supply chain with fairness concern, J. Clean Prod., 298 (2021), 126779. https://doi.org/10.1016/j.jclepro.2021.126779 doi: 10.1016/j.jclepro.2021.126779
[26]	Y. Liu, L. Ma, Y. k. Liu, A novel robust fuzzy mean-UPM model for green closed-loop supply chain network design under distribution ambiguity, Appl. Math. Model., 92 (2021), 99-135. https://doi.org/10.1016/j.apm.2020.10.042 doi: 10.1016/j.apm.2020.10.042
[27]	27. T. Asghari, A. A. Taleizadeh, F. Jolai, M. SadeghMoshtagh, Cooperative game for coordination of a green closed-loop supply chain, J. Clean Prod., 363 (2022), 132371. https://doi.org/10.1016/j.jclepro.2022.132371 doi: 10.1016/j.jclepro.2022.132371
[28]	J. Heydari, P. Rafiei, Integration of environmental and social responsibilities in managing supply chains: A mathematical modeling approach, Comput. Ind. Eng., 145 (2020), 106495. https://doi.org/10.1016/j.cie.2020.106495 doi: 10.1016/j.cie.2020.106495
[29]	Z. Feng, T. Xiao, D. J. Robb, Environmentally responsible closed-loop supply chain models with outsourcing and authorization options, J. Clean Prod., 278 (2021), 123791. https://doi.org/10.1016/j.jclepro.2020.123791 doi: 10.1016/j.jclepro.2020.123791
[30]	B. Marchi, S. Zanoni, L. E. Zavanella, M. Y. Jaber, Green supply chain with learning in production and environmental investments, IFAC-Papers OnLine, 51 (2018), 1738-1743. https://doi.org/10.1016/j.ifacol.2018.08.205 doi: 10.1016/j.ifacol.2018.08.205
[31]	Y. S. Huang, C. C. Fang, Y. A. Lin, Inventory management in supply chains with consideration of Logistics, green investment and different carbon emissions policies, Comput. Ind. Eng., 139 (2020), 106207. https://doi.org/10.1016/j.cie.2019.106207 doi: 10.1016/j.cie.2019.106207
[32]	Z. Hong, X. Guo, Green product supply chain contracts considering environmental responsibilities, Omega, 83 (2019), 155-166. https://doi.org/10.1016/j.omega.2018.02.010 doi: 10.1016/j.omega.2018.02.010
[33]	J. Cheng, B. Li, B. Gong, M. Cheng, L. Xu, The optimal power structure of environmental protection responsibilities transfer in remanufacturing supply chain, J. Clean Prod., 153 (2017), 558-569. https://doi.org/10.1016/j.jclepro.2016.02.097 doi: 10.1016/j.jclepro.2016.02.097
[34]	X. Y. Han, T. Y. Cao, Study on corporate environmental responsibility measurement method of energy consumption and pollution discharge and its application in industrial parks, J. Clean Prod., 326 (2022), 129359. https://doi.org/10.1016/j.jclepro.2021.129359 doi: 10.1016/j.jclepro.2021.129359
[35]	D. Y. Yang, D. P. Song, C. F. Li, Environmental responsibility decisions of a supply chain under different channel leaderships, Environ. Technol. Inno., 26 (2022), 102212. https://doi.org/10.1016/j.eti.2021.102212 doi: 10.1016/j.eti.2021.102212
[36]	W. Wu, Q. Zhang, Z. Liang, Environmentally responsible closed-loop supply chain models for joint environmental responsibility investment, recycling and pricing decisions, J. Clean Prod., 259 (2020), 120776. https://doi.org/10.1016/j.jclepro.2020.120776 doi: 10.1016/j.jclepro.2020.120776
[37]	R. Yang, W. S. Tang, J. X. Zhang, Government subsidies for green technology development under uncertainty, Euro J. Oper. Res., 286 (2020), 726-739. https://doi.org/10.1016/j.eti.2021.102212 doi: 10.1016/j.eti.2021.102212
[38]	S. Zheng, L. H. Yu, The government's subsidy strategy of carbon-sink fishery based on evolutionary game, Energy, 254 (2022), Part B, 124282. https://doi.org/10.1016/j.energy.2022.124282
[39]	W. T. Chen, Z. H. Hu, Using evolutionary game theory to study governments and manufacturers' behavioral strategies under various carbon taxes and subsidies, J. Clean Prod., 201 (2018), 123-141. https://doi.org/10.1016/j.jclepro.2018.08.007 doi: 10.1016/j.jclepro.2018.08.007
[40]	M. C. Cohen, R. Lobel, G. Perakis, The impact of demand uncertainty on consumer subsidies for green technology adoption, Manage. Sci., 62 (2016), 1235-1258. https://doi.org/http://hdl.handle.net/1721.1/111095
[41]	J. S. Bian, G. Q. Zhang, G. H. Zhou, Manufacturer vs. Consumer Subsidy with Green Technology Investment and Environmental Concern, Euro J. Oper. Res., 287 (2020), 832-843. https://doi.org/10.1016/j.ejor.2020.05.014 doi: 10.1016/j.ejor.2020.05.014
[42]	Y. W. Deng, N. Li, Zh. B. Jiang, X. Q. Xie, N. Kong, Optimal differential subsidy policy design for a workload-imbalanced outpatient care network, Omega, 99 (2021), 102194. https://doi.org/10.1016/j.omega.2020.102194 doi: 10.1016/j.omega.2020.102194
[43]	W. Wang, S. J. Hao, W. He, M. AbdulkadirMohamed, Carbon emission reduction decisions in construction supply chain based on differential game with government subsidies, Build Environ., (2022), 109149. https://doi.org/10.1016/j.buildenv.2022.109149
[44]	S. Chen, J. F. Su, Y. B. Wu, F. L. Zhou, Optimal production and subsidy rate considering dynamic consumer green perception under different government subsidy orientations, Comput. Ind. Eng., 168 (2022), 108073. https://doi.org/10.1016/j.cie.2022.108073 doi: 10.1016/j.cie.2022.108073
[45]	A. Suliman, H. Otrok, R. Mizouni, A greedy-proof incentive-compatible mechanism for group recruitment in mobile crowd sensing, Future Gener. Comp. Syst., 101 (2019), 1158-1167. https://doi.org/10.1016/j.future.2019.07.060 doi: 10.1016/j.future.2019.07.060
[46]	I. E. Nielsen, S. Majumder, S. S. Sana, S. Saha, Comparative analysis of government incentives and game structures on single and two-period green supply chain, J. Clean Prod., 235 (2019), 1371-1398. https://doi.org/10.1016/j.jclepro.2019.06.168 doi: 10.1016/j.jclepro.2019.06.168
[47]	W. Wang, Y. Zhang, W. Zhang, Incentive mechanisms in a green supply chain under demand uncertainty, J. Clean Prod., 279 (2021), 123636. https://doi.org/10.1016/j.jclepro.2020.123636 doi: 10.1016/j.jclepro.2020.123636
[48]	Z. Qu, H. Raff, N. Schmitt, Incentives through inventory control in supply chains, Int. J. Ind. Org., 59 (2018), 486-513. https://doi.org/10.1016/j.ijindorg.2018.06.001 doi: 10.1016/j.ijindorg.2018.06.001
[49]	Z. Wang, Z. Wang, N. Tahir, Study of synergetic development in straw power supply chain: Straw price and government subsidy as incentive, Energy Policy, 146 (2020), 111788. https://doi.org/10.1016/j.enpol.2020.111788 doi: 10.1016/j.enpol.2020.111788
[50]	Y. H. Zhang, Y. Wang, The impact of government incentive on the two competing supply chains under the perspective of Corporation Social Responsibility: A case study of Photovoltaic industry, J. Clean Prod., 154 (2017), 102-113. https://doi.org/10.1016/j.jclepro.2017.03.127 doi: 10.1016/j.jclepro.2017.03.127
[51]	H. Y. Guo, N. C. Yannelis, Incentive compatibility under ambiguity, J. Econo. Theory., 73 (2022), 565-593. https://doi.org/10.1007/s00199-020-01304-x doi: 10.1007/s00199-020-01304-x
[52]	S. Barberà, D. Berga, B. Moreno, Restricted environments and incentive compatibility in interdependent values models, Game Econo. Behav., 131 (2022), 1-28. https://doi.org/10.1016/j.geb.2021.10.008 doi: 10.1016/j.geb.2021.10.008
[53]	Y. H. Feng, S. Deb, G. G. Wang, A. H. Alavi, Monarch butterfly optimization: A comprehensive review, Expert Syst. Appl., 168 (2021), 114418. https://doi.org/10.1016/j.eswa.2020.114418 doi: 10.1016/j.eswa.2020.114418
[54]	G. G. Wang, S. Deb, Z. H. Cui, Monarch butterfly optimization, Neural Comput. Appl., 31 (2019), 1995-2014. https://doi.org/10.1007/s00521-015-1923-y doi: 10.1007/s00521-015-1923-y
[55]	H. F. Rahman, M. N. Janardhanan, L. P. Chuen, S. G. Ponnambalam, Flowshop scheduling with sequence dependent setup times and batch delivery in supply chain, Comput. Ind. Eng., 158 (2021), 107378. https://doi.org/10.1016/j.cie.2021.107378 doi: 10.1016/j.cie.2021.107378
[56]	A. Chouar, S.Tetouani, A.Soulhi, J. Elalami, Performance improvement in physical internet supply chain network using hybrid framework, IFAC-Papers OnLine, 54 (2121), 593-598. https://doi.org/10.1016/j.ifacol.2021.10.514 doi: 10.1016/j.ifacol.2021.10.514
[57]	Y. T. Yang, H. L. Chen, A. A. Heidari, A. HGandom, Hunger games search: Visions, conception, implementation, deep analysis, perspectives, and towards performance shifts, Expert Syst. Appl., 177 (2021), 114864. https://doi.org/10.1016/j.eswa.2021.114864 doi: 10.1016/j.eswa.2021.114864
[58]	H. Nguyen, X. N. Bui, A novel hunger games search optimization-based artificial neural network for predicting ground vibration intensity induced by mine blasting, Nat. Resour. Res., 30 (2021), 3865-3880. https://doi.org/10.1007/s11053-021-09903-8 doi: 10.1007/s11053-021-09903-8
[59]	R. D. Ambrosio, S. D. Giovacchino, Nonlinear stability issues for stochastic Runge-Kutta methods, Sci. Num. Simul., 94 (2021), 105549. https://doi.org/10.1016/j.cnsns.2020.105549 doi: 10.1016/j.cnsns.2020.105549
[60]	B. B. Shi, HuaYe, L. Zheng, J. C. Lyu, C. Chen, A. A. Heidari, Z. Y. Hu, H. L. Chen, P. L. Wu, Evolutionary warning system for COVID-19 severity: Colony predation algorithm enhanced extreme learning machine, Comput. Biol. Med., 136 (2021), 104698. https://doi.org/10.1016/j.compbiomed.2021.104698 doi: 10.1016/j.compbiomed.2021.104698
[61]	A. S. Mashaleh, N. F. B. Ibrahim, M. A. Al-Betar, H. M. J. Mustafa, Q. M. Yaseenc, Detecting spam email with machine learning optimized with Harris Hawks optimizer (HHO) algorithm, Procedia Comput. Sci., 201 (2022), 659-664. https://doi.org/10.1016/j.procs.2022.03.087 doi: 10.1016/j.procs.2022.03.087
[62]	M. Gen, R.W. Cheng, L. Lin, "Network Models and Optimization: Multiple Objective Genetic Algorithm Approach", 710pp, Springer, London, (2008).
[63]	X. X. Liu, J. Q. Guo, C. J. Liang, Joint Design model of multi-period reverse logistics network with the consideration of carbon emissions for e-commerce enterprises, Proceed. ICEBE2015, (2015), 428-433. https://doi.org/10.1109/ICEBE.2015.78
[64]	N. Sahebjamnia, A. M. Fathollahi-Fard, M. Hajiaghaei-Keshteli, Sustainable tire closed-loop supply chain network design: Hybrid meta-heuristic algorithms for large-scale networks, J. Clean Prod., 196 (2018), 273-296. https://doi.org/10.1016/j.jclepro.2018.05.245 doi: 10.1016/j.jclepro.2018.05.245
[65]	J. Y. Feng, B. Y. Yuan, X. Li, D. Tian, W. S. Mu, Evaluation on risks of sustainable supply chain based on optimized BP neural networks in fresh grape industry, Agriculture, 183 (2021), 105988. https://doi.org/10.1016/j.compag.2021.105988 doi: 10.1016/j.compag.2021.105988
[66]	S. X. Zhao, Y. C. Wang, Z. Y. Jiang, T. S. Hu, F. M. Chu, Research on emergency distribution optimization of mobile power for electric vehicle in photovoltaic-energy storage-charging supply chain under the energy blockchain, Energy Rep., 8 (2022), 6815-6825. https://doi.org/10.1016/j.egyr.2022.05.010 doi: 10.1016/j.egyr.2022.05.010
[67]	X. Y. Wang, J. Q. Guo, Optimal strategies of different quality level of returned Products for manufacturing/remanufacturing enterprises under carbon tax, Resour. Develop. mkt., 33 (2017), 59-63. https://doi.org/10.3969/j.issn.1005-8141.2017.01.011 doi: 10.3969/j.issn.1005-8141.2017.01.011
[68]	J. Q. Guo, L. He, M. Gen, Optimal strategies for the closed-loop supply chain with the consideration of supply disruption and subsidy policy, Comput. Ind. Eng., 128 (2019), 886-893. https://doi.org/10.1016/j.cie.2018.10.029 doi: 10.1016/j.cie.2018.10.029
[69]	N. Wan, D. Hong, The impacts of subsidy policies and transfer pricing policies on the closed-loop supply chain with dual collection channels, J. Clean Prod., 224 (2019), 881-891. https://doi.org/10.1016/j.jclepro.2019.03.274 doi: 10.1016/j.jclepro.2019.03.274
[70]	J. Q. Guo, Y. Gao, Optimal strategies for manufacturing/remanufacturing system with the consideration of recycled products, Comput. Ind. Eng., 89 (2015), 226-234. https://doi.org/10.1016/j.cie.2014.11.020 doi: 10.1016/j.cie.2014.11.020
[71]	Y. Yu, X. Han, G. Hu, Optimal production for manufacturers considering consumer environmental awareness and green subsidies, Int. J. Prod. Econ., 182 (2016), 397-408. https://doi.org/10.1016/j.cie.2022.108073 doi: 10.1016/j.cie.2022.108073
[72]	X. Gu, L. Zhou, H. Huang, X. Shi, Electric vehicle battery secondary use under government subsidy: A closed-loop supply chain perspective, Int. J. Prod. Econ., 234 (2021), 108035. https://doi.org/10.1016/j.ijpe.2021.108035 doi: 10.1016/j.ijpe.2021.108035
[73]	N. Wang, Y. Song, Q. He, T. Jia, Competitive dual-collecting regarding consumer behavior and coordination in closed-loop supply chain, Comput. Ind. Eng., 144 (2020), 106481. https://doi.org/10.1016/j.cie.2020.106481 doi: 10.1016/j.cie.2020.106481
[74]	S. M. Hosseini-Motlagh, M. Johari, S. Ebrahimi, P. Rogetzer, Competitive channels coordination in a closed-loop supply chain based on energy-saving effort and cost-tariff contract, Comput. Ind. Eng., 149 (2020), 106763. https://doi.org/10.1016/j.cie.2020.106763 doi: 10.1016/j.cie.2020.106763
[75]	J. Q. Guo, Y. D. Kao, H. Huang, A manufacturing/remanufacturing system with the consideration of required quality of end-of-used products, Indus. Eng. Mgt. Syst., 9 (2010), 204-214. https://doi.org/10.7232/iems.2010.9.3.204 doi: 10.7232/iems.2010.9.3.204
[76]	Y. Wu, R. Lu, J. Yang, R. Wang, H. Xu, C. Jiang, F. Xu, Government-led low carbon incentive model of the online shopping supply chain considering the O2O model, J. Clean Prod., 279 (2021), 123271. https://doi.org/10.1016/j.jclepro.2020.123271 doi: 10.1016/j.jclepro.2020.123271
[77]	X. Wan, X. Qie, Poverty alleviation ecosystem evolutionary game on smart supply chain platform under the government financial platform incentive mechanism, J. Comput. Appl. Math., 372 (2020), 112595. https://doi.org/10.1016/j.cam.2019.112595 doi: 10.1016/j.cam.2019.112595
[78]	J. Bian, G. Zhang, G. Zhou, Manufacturer vs. Consumer subsidy with green technology investment and environmental concern, Euro. J. Oper. Res., 287 (2020), 832-843. https://doi.org/10.1016/j.ejor.2020.05.014 doi: 10.1016/j.ejor.2020.05.014
[79]	W. Wu, Q. Zhang, Z. Liang, Environmentally responsible closed-loop supply chain models for joint environmental responsibility investment, recycling and pricing decisions, J. Clean Prod., 259 (2020), 120776. https://doi.org/10.1016/j.jclepro.2020.120776 doi: 10.1016/j.jclepro.2020.120776
[80]	S. Nayeri, M. M. Paydar, E. Asadi-Gangraj, S. Emami, Multi-objective fuzzy robust optimization approach to sustainable closed-loop supply chain network design, Comput. Ind. Eng., 148 (2020), 106716. https://doi.org/10.1016/j.cie.2020.106716 doi: 10.1016/j.cie.2020.106716
[81]	K. Bhattacharya, S. D. Kumar, A robust two layer green supply chain modelling under performance based fuzzy game theoretic approach, Comput. Ind. Eng., 152 (2021), 107005. https://doi.org/10.1016/j.cie.2020.107005 doi: 10.1016/j.cie.2020.107005
[82]	M. Yavari, S. Isvandi, Integrated decision making for parts ordering and scheduling of jobs on two-stage assembly problem in three level supply chain, J. Manuf. Syst., 46 (2018), 137-151. https://doi.org/10.1016/j.jmsy.2017.12.002 doi: 10.1016/j.jmsy.2017.12.002
[83]	J. Wu, Y. Ding, L. Shi, Mathematical modeling and heuristic approaches for a multi-stage car sequencing problem, Comput. Ind. Eng., 152 (2021), 107008. https://doi.org/10.1016/j.cie.2020.107008 doi: 10.1016/j.cie.2020.107008
[84]	M. Hamdi, M. Zaied, Resource allocation based on hybrid genetic algorithm and particle swarm optimization for D2D multicast communications, Appl. Soft Comput., 83 (2019), 105605. https://doi.org/10.1016/j.asoc.2019.105605 doi: 10.1016/j.asoc.2019.105605
[85]	A. Afzal, M., K. Ramis, Multi-objective optimization of thermal performance in battery system using genetic and particle swarm algorithm combined with fuzzy logics, J. Energy Stor., 32 (2020), 101815. https://doi.org/10.1016/j.est.2020.101815 doi: 10.1016/j.est.2020.101815
[86]	M. Gen, L. Lin, Y.S. Yun, H. Inoue, Recent advances in hybrid priority-based genetic algorithms for logistics and SCM network design, Comput. Ind. Eng., 115 (2018), 394-412. https://doi.org/10.1016/j.cie.2018.08.025 doi: 10.1016/j.cie.2018.08.025
[87]	G. Ahn, S. Hur, Efficient genetic algorithm for feature selection for early time series classification, Comput. Ind. Eng., 142 (2020), 106345. https://doi.org/10.1016/j.cie.2020.106345 doi: 10.1016/j.cie.2020.106345
[88]	A. Rostami, M. M. Paydar, E. Asadi-Gangraj, A hybrid genetic algorithm for integrating virtual cellular manufacturing with supply chain management considering new product development, Comput. Ind. Eng., 145 (2020), 106565. https://doi.org/10.1016/j.cie.2020.106565 doi: 10.1016/j.cie.2020.106565

This article has been cited by:

1.	Yangang Feng, Xuemeng Li, Remanufacturing closed-loop supply chain decision comparison under multiple carbon policies, 2024, 9, 2444-8656, 10.2478/amns-2024-1052
2.	Jianquan Guo, Lian Chen, Configuration and optimisation of a green closed-loop supply chain with delivery time and green investment considering government subsidy under meta-heuristics algorithms, 2024, 11, 2330-2674, 10.1080/23302674.2024.2401033
3.	Jianquan Guo, Lian Chen, Zhen Wang, Optimization of a closed-loop supply chain system considering government incentives mechanism under deep learning algorithms, 2025, 03608352, 111146, 10.1016/j.cie.2025.111146

Reader Comments

Your name:*

Email:*
© 2022 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)

通讯作者: 陈斌, bchen63@163.com

1.
沈阳化工大学材料科学与工程学院沈阳 110142

Mathematical Biosciences and Engineering

3.9

Metrics

Article views(2828) PDF downloads(152) Cited by(3)

Preview PDF

Download XML

Export Citation

Article outline

Show full outline

Figures and Tables

Figures(9) / Tables(6)

Mathematical Biosciences and Engineering

Green closed-loop supply chain optimization strategy considering CER and incentive-compatibility theory under uncertainty

Related Papers:

Abstract

1. Introduction

2. Problem deﬁnitions, notations, and assumptions

2.1. Problem deﬁnitions

2.2. Notations

2.2.1. Input parameters

2.2.2. Output parameters

2.2.3. Decision variables

2.3. Assumptions

3. Mathematical modeling

3.1. Cost of new products

3.1.1. Setup cost for manufacturing

3.1.2. Ordering cost

3.1.3. Raw material holding cost

3.1.4. Manufacturing cost

3.1.5. Inventory costs of raw material and new products

3.2. Cost of remanufactured products

3.2.1. Setup cost for remanufacturing

3.2.2. Buyback cost

3.2.3. Remanufacturing cost

3.2.4. Inventory costs of recycled products and remanufacturing products

3.3. Incentive-compatibility functions

3.3.1. Incentive function

3.3.2. Compatibility function

3.4. Average gross profit

3.5. Fuzzy chance constrained clarifications

4. Solution techniques

4.1. Genetic algorithm

5. Numerical experiments

5.1. Numerical results

5.1.1. Optimal decision under uncertain environment

5.1.2. Optimal decision under no government subsidy

5.1.3. Optimal decision under government differential weighting subsidy

5.1.4. Effect comparison before and after incentive-compatibility theory

5.2. Discussion (Managerial insights and main achievements)

6. Conclusions

Acknowledgments

Conflict of interest

References

This article has been cited by:

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Related pages

Tools

Export File

Citation

Format

Content

Catalog